zunia.vn

Tuyển sinh 2024 dành cho Gen-Z

zunia.vn

» Tài Liệu Phổ Thông

» Đề thi - Kiểm tra

ĐỀ KIỂM TRA CHỌN HỌC SINH GIỎI (ĐẦU NĂM) MÔN : TOÁN LỚP 8 THCS Nguyễn Khuyến Đà Nẵng

Chia sẻ: Bùi Hồng Ngọc | Ngày: | Loại File: DOC | Số trang:4

Báo xấu

209
lượt xem 18
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Cho tam giác ABC vuông cân tại A. Gọi M là một điểm nằm giữa Avà B. Trên tia đối của tia AC lấy điểm I sao cho AI = AM. a) Chứng minh rằng : CM ^ BI. b) Trên BC lấy điểm P sao cho BP = 2CP. Trên nửa mặt phẳng bờ là đường thẳng BC có chứa điểm A, vẽ tia Px sao cho góc xPB bằng 600 . Tia Px cắt tia CA tại D. Tính số đo góc CBD .

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: ĐỀ KIỂM TRA CHỌN HỌC SINH GIỎI (ĐẦU NĂM) MÔN : TOÁN LỚP 8 THCS Nguyễn Khuyến Đà Nẵng

Giáo viênTôn Nữ Bích Vân-Trường THCS Nguyễn Khuyến Đà Nẵng ĐỀ KIỂM TRA CHỌN HỌC SINH GIỎI (ĐẦU NĂM) MÔN : TOÁN LỚP 8 Thời gian: 90 phút (không kể thời gian giao đề) 2 1 Bài 1 (2 điểm): Tìm x biết: a) | x – |< 3 3 x b) – 3 = – 6561 c) (2x – 1)2008 = (2x – 1)2010 2009 Bài 2 (2 điểm): a) Số tự nhiên có dạng A = 1+23 là số nguyên tố hay hợp số? Giải thích. b) Tìm giá trị nhỏ nhất của B = 2x2 + y2 +2xy – 8x + 2025 c) Tìm x, y, z biết : 10x2 + y2 + 4z2 + 6x – 4y – 4xz + 5 = 0 2 3 Bài 3 (1,5 điểm ): Một khối 8 có số học sinh đội tuyển Toán bằng số học sinh 3 4 4 đội tuyển Anh và bằng số học sinh đội tuyển Văn. Đội tuyển Văn có số học sinh 5 ít hơn tổng số học sinh của hai đội tuyển kia là 38 học sinh. Tính s ố h ọc sinh c ủa mỗi đội tuyển. Bài 4 (1,5 điểm): Cho x(m + n) = y(n + p) = z(p + m) trong đó x, y, z là các số khác m− n n−p p− m = = nhau và khác 0 ,chứng minh rằng: x(y − z) y(z − x) z(x − y ) Bài 5 (3điểm ): Cho tam giác ABC vuông cân tại A. Gọi M là một đi ểm n ằm gi ữa Avà B. Trên tia đối của tia AC lấy điểm I sao cho AI = AM. a) Chứng minh rằng : CM ⊥ BI. b) Trên BC lấy điểm P sao cho BP = 2CP. Trên nửa mặt ph ẳng bờ là đường th ẳng BC có chứa điểm A, vẽ tia Px sao cho góc xPB bằng 60 0 . Tia Px cắt tia CA tại D. Tính số đo góc CBD .
Giáo viênTôn Nữ Bích Vân-Trường THCS Nguyễn Khuyến Đà Nẵng ĐÁP ÁN KIỂM TRA HỌC SINH GIỎI MÔN :TOÁN LỚP 8 Bài 1(2 điểm): 1 21 21 1 a) | x − | < ⇔ − < x − < ⇔
Giáo viênTôn Nữ Bích Vân-Trường THCS Nguyễn Khuyến Đà Nẵng (x + y) − z x y z 38 = = = = =2 ⇒ (0,5điểm) 18 16 15 (18 + 16) − 15 19 Tính đúng: x = 36; y = 32; z = 30 và kết luận (0,5điểm) Bài 4(1,5 điểm ) : Vì xyz ≠ 0 nên : x(m + n) = y(n + p) = z(p + m) x(m + n) y( n + p) z(p + m) = = ⇒ (0,25 điểm) xyz xyz xyz m+ n n+ p p+ m = = (0,25 điểm) hay : yz xz xy (p + m) − ( n + p) (m + n) − (p + m) ( n + p) − (m + n) = = (0,5điểm) = xy − xz yz − xy xz − yz m− n n−p p− m = = (0,5điểm) = x(y − z) y(z − x) z(x − y ) Bài 5(3điểm): Hình vẽ (0,25điểm) a)Tia IM cắt BC tại H (0,25điểm) ∧ ∧ ∆ABC vuông cân tại A nên C = 450 , ∆IAM vuông cân tại M nên I = 450 ∧ ∧ ∧ (0,25điểm) ∆IHC có C + I = 900 ⇒ H = 900 ⇒ IH ⊥ BC (0,25điểm) -Chứng minh được M là trực tâm của ∆IBC ⇒ CM ⊥ BI. (0,5điểm) b) Gọi E là điểm đối xứng với B qua PD ⇒ EP = PB = 2PC (0,25điểm) ⇒ ∆ BPE cân tại P nên đường trung trực PD cũng là phân giác ⇒ BPD = DPE = 600 ⇒ EPC = 600 (0,25điểm) - Chứng minh được ∆EPC vuông tại C (0,25điểm) - Chứng minh được CD là phân giác của ∆ PCE - Chứng minh được ED là phân giác ngoài tại đỉnh E của ∆ PCE (0,25điểm) - Chứng minh được yEP = 1500 ⇒ DEP = 750 (0,25điểm) - Chứng minh được PBD = 750 hay CBD = 750 (0,25điểm)
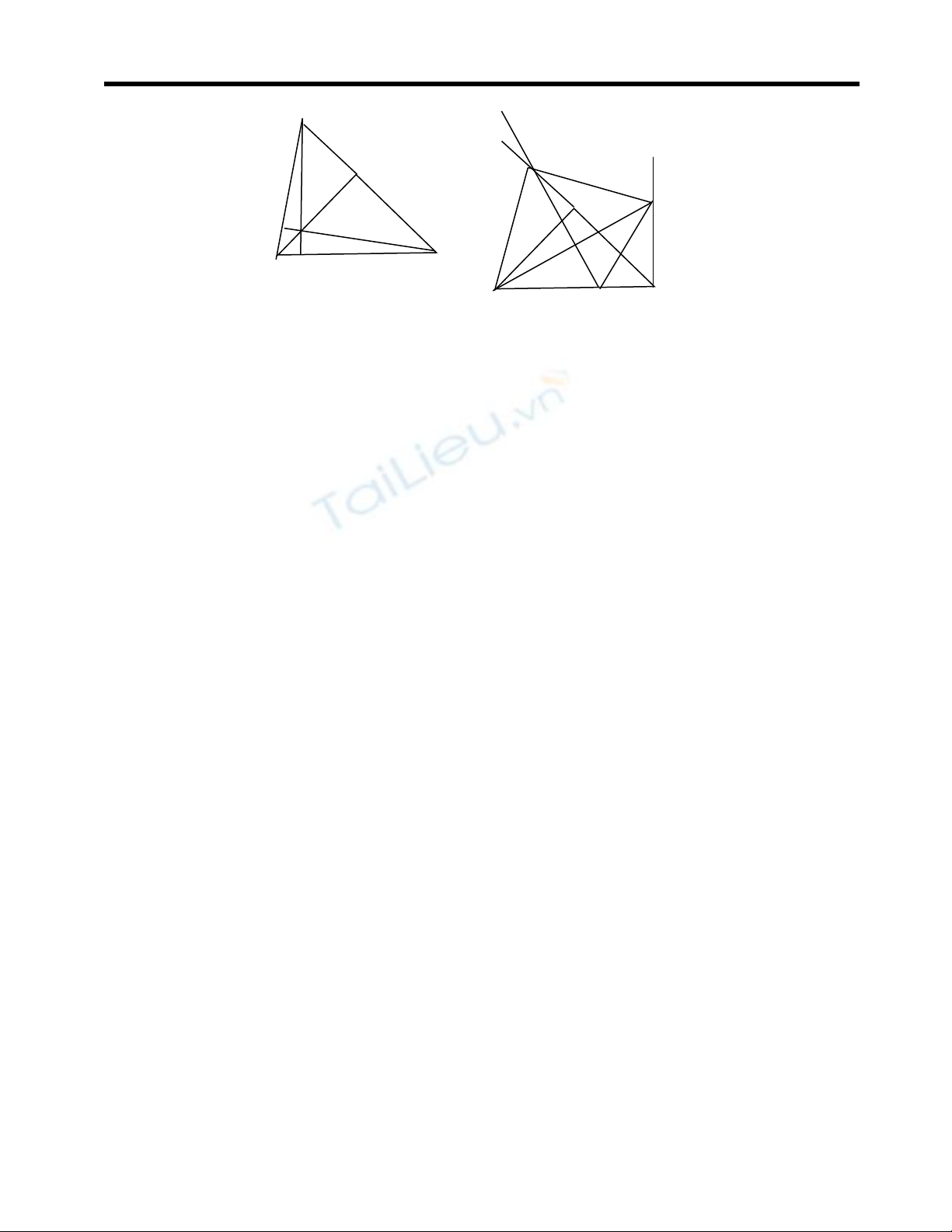
Giáo viênTôn Nữ Bích Vân-Trường THCS Nguyễn Khuyến Đà Nẵng I x A y D A E M K H C B C P B *Chú ý :Học sinh có thể giải cách khác, nếu chính xác thì hưởng trọn số điểm câu đó.

CÓ THỂ BẠN MUỐN DOWNLOAD

EXAM.03: Bộ 400 Đề Thi Thử THPT Quốc Gia 2021

400 tài liệu

955 lượt tải

THÔNG TIN

TRỢ GIÚP

HỖ TRỢ KHÁCH HÀNG

Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.