1
TRƯỜNG THPT BẾN TRE
TỔ: TOÁN – TIN
ĐỀ KIỂM TRA 45 PHÚT CHƯƠNG 1 NĂM HỌC 2018 – 2019
MÔN: GIẢI TÍCH 12
Thời gian làm bài: 45 phút;
(25 câu trắc nghiệm)
Câu 1. Tìm tất cả các giá trị thực của tham số m sao cho hàm số sau luôn nghịch biến trên
R
?
32
1(2 3) 2
3
yxmxmxm
A. 31m . B. 1m. C. 31m . D. 3; 1mm .
Câu 2. Cho hàm số 3
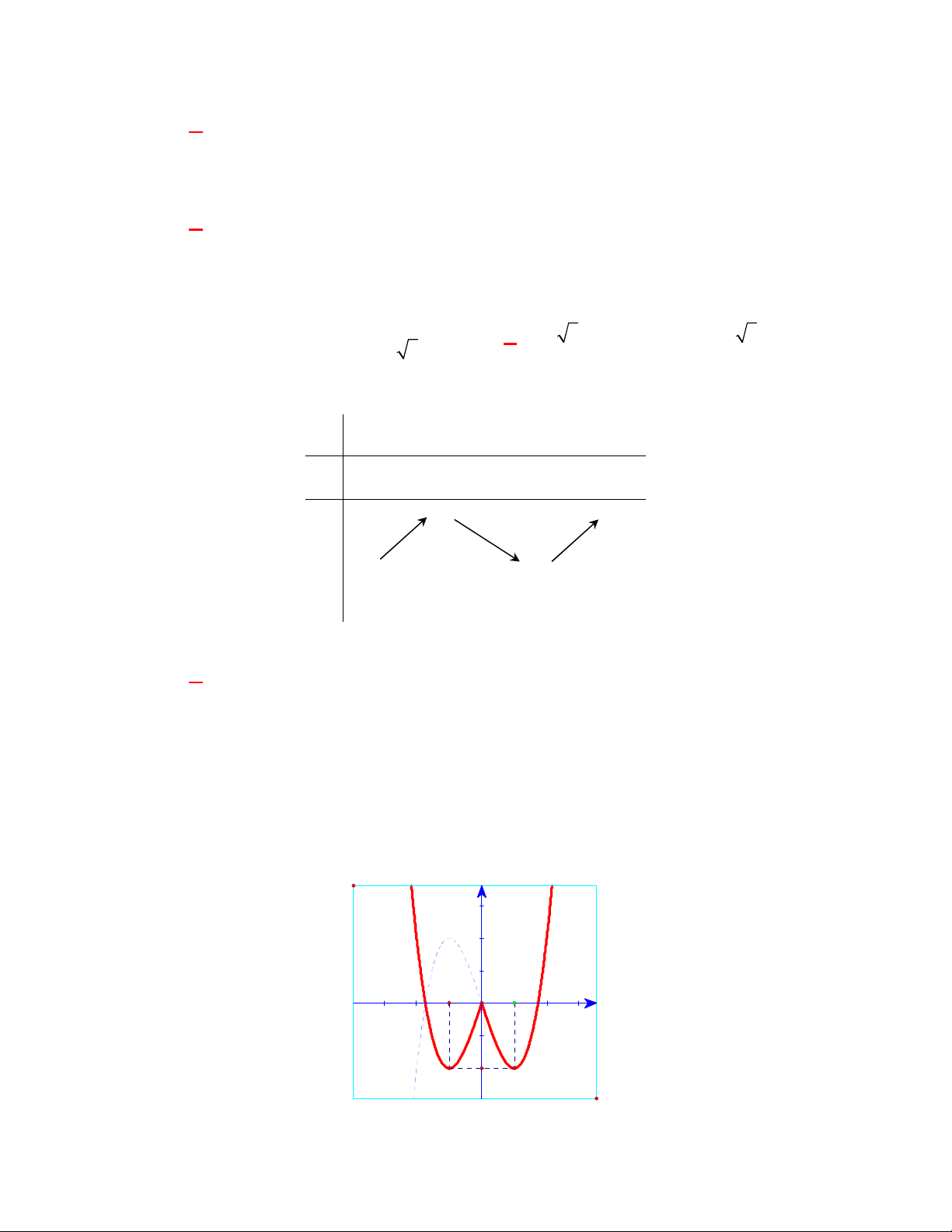
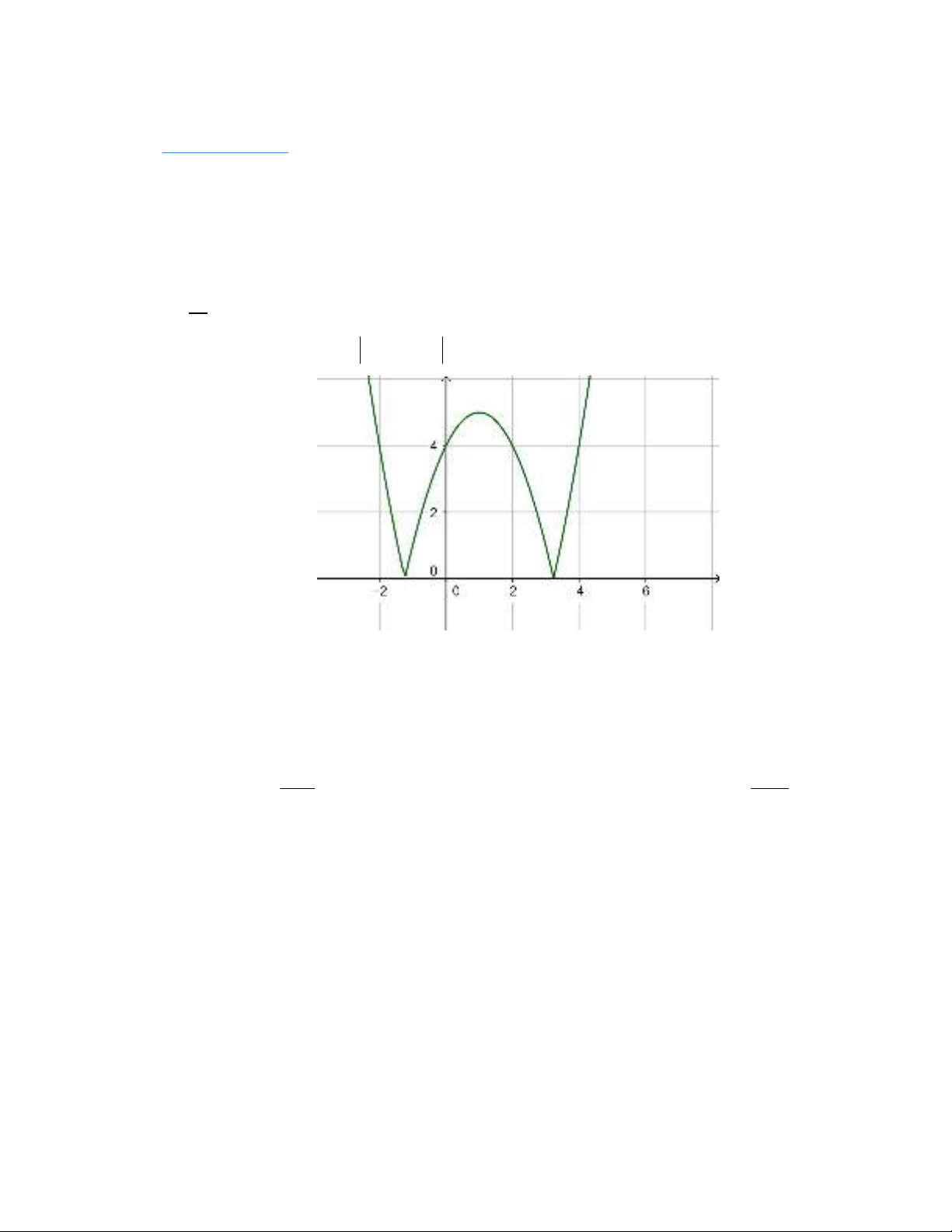
|32|yx x có đồ thị như hình vẽ:
Khẳng định nào sau đây là khẳng định đúng?
A. Đồ thị hàm số ()yfx chỉ có điểm cực tiểu và không có điểm cực đại.
B. Đồ thị hàm số ()yfx có một điểm cực tiểu và một điểm cực đại.
C. Đồ thị hàm số ()yfx có bốn điểm cực trị.
D. Đồ thị hàm số ()yfx có một điểm cực đại và hai điểm cực tiểu.
Câu 3. Hàm số nào sau đây không có cực trị?
A. 2
2.
1
yx
x
B. 32
3.
y
xx C. 42
23.yx x D. 1.
2
x
y
x
Câu 4. Hàm số 422
2( 2) 2 3yx m x m m có đúng 1 điểm cực trị thì giá trị của m là:














![[TRÙNG] Đề kiểm tra giữa HK1 môn Toán 12 năm 2019-2020 có đáp án - Trường THPT Ten Lơ Man](https://cdn.tailieu.vn/images/document/thumbnail/2020/20201102/lianhuawu/135x160/6991604282187.jpg)























