PHÒNG GD&ĐT Đ KI M TRA KH O SÁT Đ U NĂMỀ Ể Ả Ầ
TH XÃ PHÚ THỊ Ọ Năm h c 2011-2012ọ
MÔN: TOÁN L P 8Ớ
Th i gian làm bài 60 phút ( không k th i gian giao đ )ờ ể ờ ề
Câu 1.(2 đi mể)
Cho đ n th c A = ơ ứ
( )
2 3
1. 3
2x y xy
−
÷
a) Thu g n đ n th c Aọ ơ ứ
b) Xác đ nh ph n h s , ph n bi n, b c c a đ n th c.ị ầ ệ ố ầ ế ậ ủ ơ ứ
c) Tính giá tr c a A khi x = -1; y = -1.ị ủ
Câu 2. (3 đi mể)
Cho hai đa th c sau :ứ
P(x) = - 7x2 + 6 – 4x4 + 3x – 9x3 và
Q(x) = 3x4 + 5x – 3x2 + 7x3 – 8 .
a) Hãy s p x p các h ng t c a m i đa th c trên theo lu th a gi m d nắ ế ạ ử ủ ỗ ứ ỹ ừ ả ầ
c a bi n . ủ ế
b) Tính P(x) + Q(x) và P(x) – Q(x)
Câu 3. ( 4 đi mể)
Cho tam giác ABC cân t i A . H là trung đi m c a BC . ạ ể ủ
a) Ch ng minh : ứ
∆
AHB =
∆
AHC .
b) V HE ẽ
⊥
AB ; HF
⊥
AC (E
∈
AB ; F
∈
AC) . Ch ng minh AE =ứ
AF .
c) Bi t s đo ế ố
·
0
50BAH =
. Tính s đo ố
·
?AHE =
d) Gi s AB = 5 cm , BC = 8 cm . Tính AH ?ả ử
Câu 4. (1.0 đi mể)
Cho đa th c f(x) th a mãn đi u ki n : ứ ỏ ề ệ
. ( 2) ( 4). ( )x f x x f x− = −
. Ch ngứ
minh r ng đa th c f(x) có ít nh t 2 nghi mằ ứ ấ ệ
PHÒNG GD&ĐT HDC KI M TRA KH O SÁT Đ U NĂM Ể Ả Ầ
TH XÃ PHÚ THỊ Ọ Năm h c 2011-2012ọ
MÔN: TOÁN L P 8Ớ
M t s chú ý khi ch m bài:ộ ố ấ
H ng d n ch m d i đây có 2 trang và d a vào l i gi i s l c c a m tướ ẫ ấ ướ ự ờ ả ơ ượ ủ ộ
cách. Thí sinh gi i cách khác mà cho k t qu đúng thì cho đi m t ng ph n ngả ế ả ể ừ ầ ứ
v i thang đi m c a H ng d n ch m.ớ ể ủ ướ ẫ ấ
Câu Đáp án Điể
m
Câu 1.(2 đi mể) Cho đ n th c A = ơ ứ
( )
2 3
1. 3
2x y xy
−
÷
a) Thu g n đ n th c Aọ ơ ứ
b) Xác đ nh ph n h s , ph n bi n, b c c a đ n th c.ị ầ ệ ố ầ ế ậ ủ ơ ứ
c) Tính giá tr c a A khi x = -1; y = -1.ị ủ
a) Thu g n đ n th c A = ọ ơ ứ
=
( )
2 3
1.( 3) .
2x yxy
−
÷
=
3 4
3
2x y−
0,5
b)
Ph n h s là: ầ ệ ố
3
2
−
Ph n bi n là: ầ ế
3 4
x y
Bc c a đ n th c là: 7ậ ủ ơ ứ
0,75
c) V i x = ớ-1 ; y = -1, ta có : A =
3 4
3
2x y−
=
3
2
−
. (-1)3.(-1)4 =
3
2
0,75
Câu 2. (3 đi mể) Cho hai đa th c sau :ứ
P(x) = - 7x2 + 6 – 4x4 + 3x – 9x3 và Q(x) = 3x4 + 5x – 3x2 + 7x3 – 8 .
a/ Hăy s p x p các h ng t c a m i đa th c trên theo lu th a gi m d n c aắ ế ạ ử ủ ỗ ứ ỹ ừ ả ầ ủ
bi n. ế
b/ Tính P(x) + Q(x) và P(x) – Q(x)
a) P(x) = - 7x2 + 6 – 4x4 + 3x – 9x3 = - 4x4 – 9x3 - 7x2 + 3x + 6 0,5
Q(x) = 3x4 + 5x – 3x2 + 7x3 – 8 = 3x4 +7x3 – 3x2 + 5x – 8 0,5
b)
P(x) + Q(x) = - 4x4 – 9x3 - 7x2 + 3x + 6 +3x4 +7x3 –3x2 + 5x – 8
= - x4 – 2x3 –10x2 +8x - 2 1,0
P(x) – Q(x) =(- 4x4 – 9x3 - 7x2 + 3x + 6) – (3x4 +7x3 –3x2 + 5x – 8)
= - 4x4 – 9x3 - 7x2 + 3x + 6 – 3x4 -7x3 +3x2 - 5x + 8)
= - 7x4– 16x3 - 4x2- 2x +14
1,0
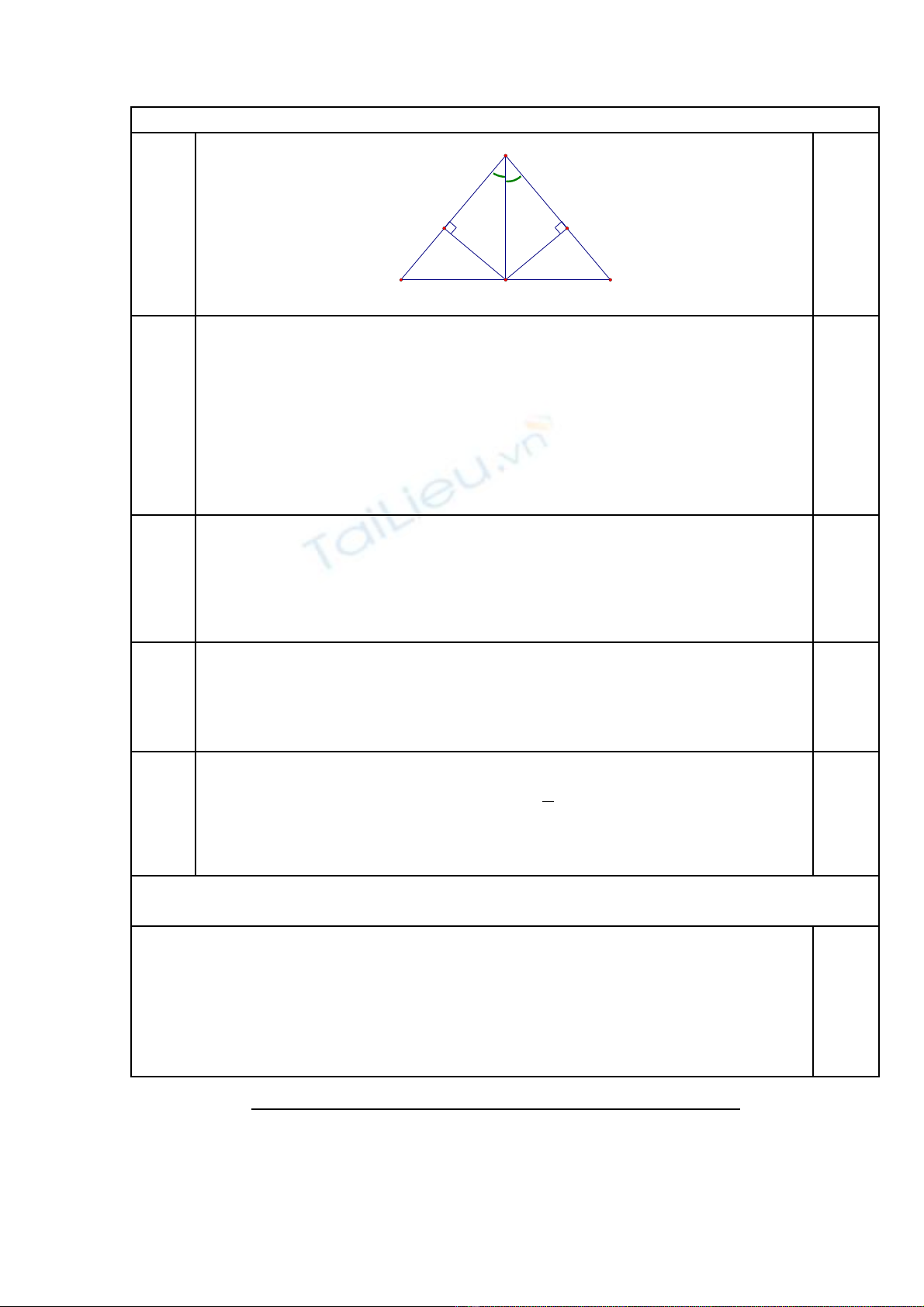
Câu 3. ( 4 đi mể) Cho tam giác ABC cân t i A . H là trung đi m c a BC . ạ ể ủ
a) Ch ng minh : ứ
∆
AHB =
∆
AHC .
b) V HE ẽ
⊥
AB ; HF
⊥
AC (E
∈
AB ; F
∈
AC) . Ch ng minh AE = AF . ứ
c) Bi t s đo ế ố
·
0
50BAH =
. Tính s đo ố
·
?AHE =
PHÒNG GD&ĐT HDC KI M TRA KH O SÁT Đ U NĂM Ể Ả Ầ
d) Gi s AB = 5 cm , BC = 8 cm . Tính AH ?ả ử
2
1
F
E
H
C
B
A
0,5
a) Ch ng minh : ứ
∆
AHB =
∆
AHC
∆
cân ABC có AH là trung tuy n nên AH cũng là phân giác hayế
· ·
BAH CAH=
Xét
∆
AHB và
∆
AHC có:
·
·
AB AC (gt)
BAH = CAH (CMT) AHB AHC (c.g.c)
AH là canh chung
=
⇒ ∆ = ∆
1,0
b) Ch ng minh AE = AFứ
Xét 2 tam giác vuông AHE và AHF có c nh huy n AH chung và cóạ ề
·
·
EAH FAH=
⇒ ∆
AHE=
∆
AHF (C nh huy n, góc nh n) ạ ề ọ
⇒
các c nh t ngạ ươ
ng b ng nhau hay AE = AFứ ằ
1,0
c) Bi t s đo ế ố
·
0
50BAH =
. Tính s đo ố
·
?AHE =
Xét tam giác AHE là tam giác vuông có
· ·
0
40BAH EAH= =
mà trong
tam giác vuông 2 góc nh n ph nhau nênọ ụ
·
·
0 0 0 0
90 90 50 40AHE EAH=− =−=
1,0
d) Gi s AB = 5 cm , BC = 8 cm . Tính AHả ử
Vì H là trung đi m c a BC nên BH = ể ủ
1
2
BC = 4 cm
Áp d ng đ nh lý Pitago vào tam giác vuông ABH ta có AHụ ị 2 + BH2 = AB2
⇒
AH2 = AB2 – BH2 = 52 – 42 = 9
⇒
AH = 3cm
1.0
Câu 4. (1.0 đi mể) Cho đa th c f(x) th a mãn đi u ki n : ứ ỏ ề ệ
. ( 2) ( 4). ( )x f x x f x− = −
.
Ch ng minh r ng đa th c f(x) có ít nh t 2 nghi mứ ằ ứ ấ ệ
Ta có
. ( 2) ( 4). ( ) (1)x f x x f x− = −
v i m i x ớ ọ
Thay x = 0 vào (1) a đ c: ượ
0. (0 2) (0 4). (0)f f− = −
hay
0. ( 2) 4. (0)f f− = −
4. (0) 0 (0) 0f f⇒ − = ⇒ =
. Nên 0 là m t nghi m c a f(x).ộ ệ ủ
Thay x = 2 vào (1) ta đ c: ượ
2. (2 2) (2 4). (2)f f− = −
hay
2. (0) 2. (2) . (2) (0) 0f f f f= − ⇒ = =
. V y 2 cũng là m t nghi m c a f(x). ậ ộ ệ ủ
Do đó f(x) ó ít nh t 2 nghi m là 0 và 2ấ ệ
1,0