S GD&ĐT QU NG NAMỞ Ả
TR NG THPT CAO BÁ QUÁTƯỜ
Đ s 6ề ố
Đ THI H C KÌ 1 – Năm h c 2010 – 2011Ề Ọ ọ
Môn TOÁN L p 11ớ
Th i gian làm bài 90 phútờ
I. Ph n chung (7 đi m)ầ ể
Câu 1 (2 đi m):ể Gi i các ph ng trình l ng giác sau:ả ươ ượ
a)
x3
sin2 2
= −
b)
x0 0
cot( 15 ) tan45+ =
c) 3sinx + cos2x – 3 = 0
Câu 2 (2 đi m):ể
a) Khai tri n nh th c (2ể ị ứ a + b)5 thành đa th c? Tìm h s c a ứ ệ ố ủ a2b3 trong khai tri n trên?ể
b) M t chi c h p có 8 qu c u xanh và 6 qu c u vàng. L y ng u nhiên 5 qu c u. Gi s cácộ ế ộ ả ầ ả ầ ấ ẫ ả ầ ả ử
qu c u ch khác nhau v màu. Tính xác su t c a bi n c A: ”Trong 5 qu c u l y ra có đúng 3ả ầ ỉ ề ấ ủ ế ố ả ầ ấ
qu c u xanh”?ả ầ
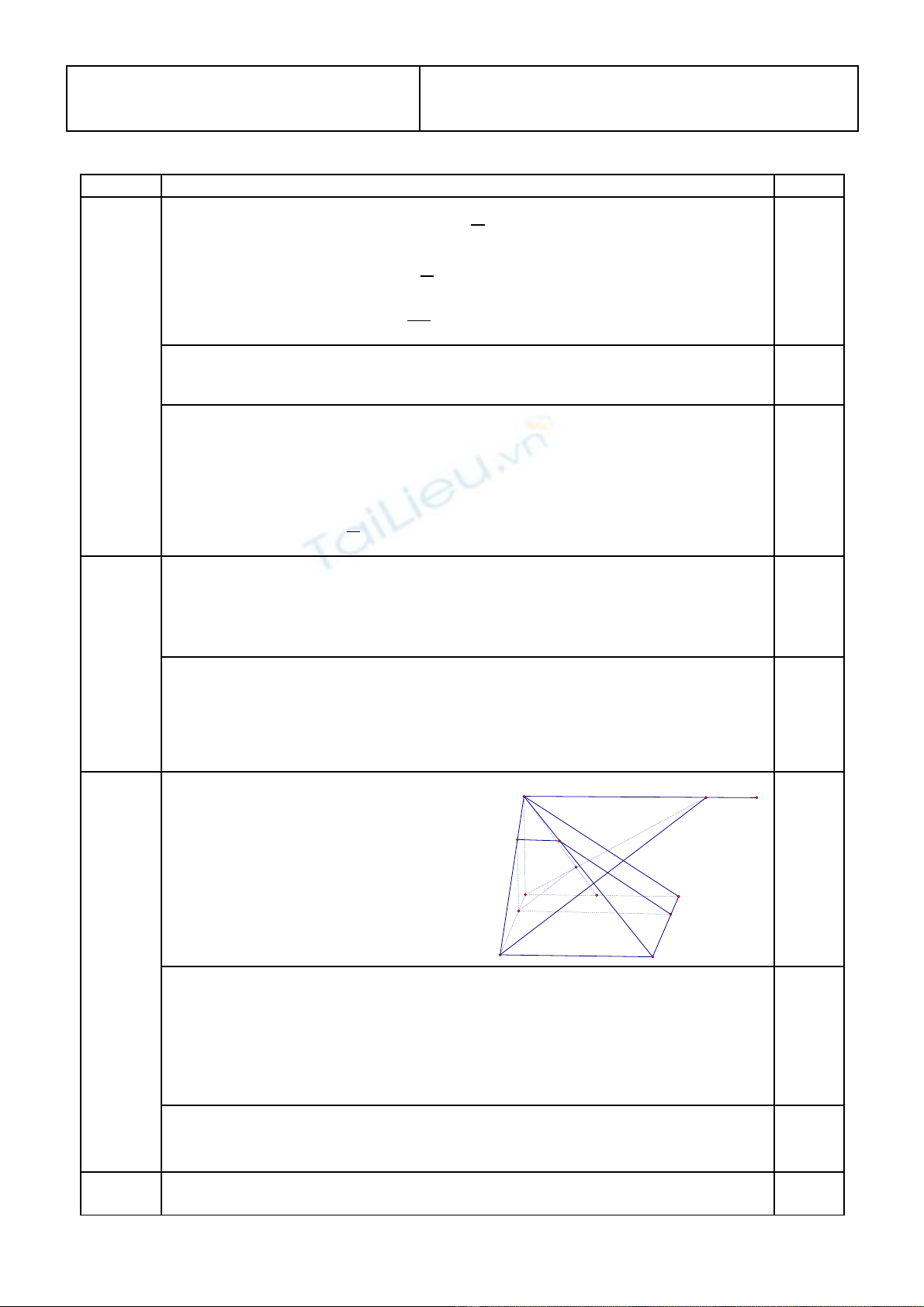
Câu 3 (3 đi m): ểCho hình chóp SABCD v i đáy ABCD là hình bình hành. ớG i G là tr ng tâm ọ ọ ∆SAB.
L y đi m M thu c c nh AD sao cho AD = 3AM.ấ ể ộ ạ
a) Tìm giao tuy n c a (SAB) và (SCD)?ế ủ
b) M t ph ng (ặ ẳ α) đi qua M và song song v i SA, CD. Tìm thi t di n c a m t ph ng (ớ ế ệ ủ ặ ẳ α) v i hìnhớ
chóp? Thi t di n đó là hình gì?ế ệ
c) Ch ng minh MG song song v i mp(SCD) .ứ ớ
II. Ph n riêng (3 đi m:ầ ể
A. Theo ch ng trình chu nươ ẩ :
Câu 4a (1 đi m):ể Ch ng minh r ng ứ ằ ∀n∈N* ta có: 2 + 4 + 6+ ….. + 2n = n(n+1)
Câu 5a (1 đi mể): Trong m t ph ng Oặ ẳ xy, cho đ ng tròn (C) có tâm I(1; –2) và R = 2. Hãy vi t ph ngườ ế ươ
trình c a đ ng tròn (Củ ườ ′) là nh c a (C) qua phép v t tâm A(3; 1), t s ả ủ ị ự ỉ ố k = –2 .
Câu 6a (1 đi m):ể Gi i ph ng trình: ả ươ sin3x + cos2x = 1 + 2sinxcos2x
B.Theo ch ng trình nâng caoươ :
Câu 4b (1 đi m): ểGi i ph ng trìnhả ươ 9sinx + 6cosx – 3sin2x + cos2x = 8
Câu 5b (1đi m):ể Tìm h s c a ệ ố ủ
x
31 trong khai tri n c a ể ủ
n
x
x2
1
� �
+
� �
� �
, bi t r ng ế ằ
n n
n n n
C C A
1 2
1821
2
−
+ + =
.
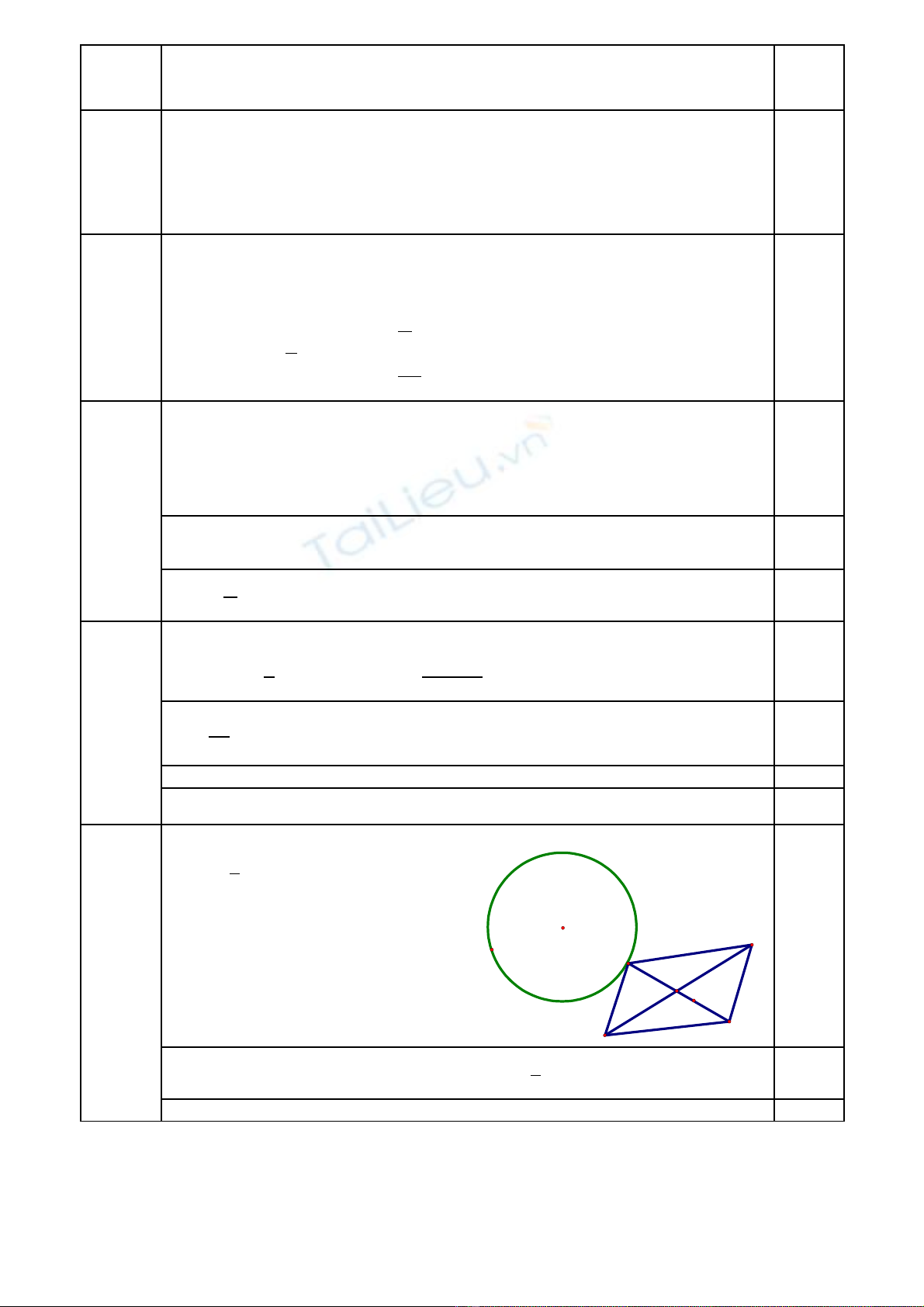
Câu 6b (1 đi m):ể Cho đ ng tròn C(O, R) và hai đi m B, D c đ nh sao cho đ ng th ng BD khôngườ ể ố ị ườ ẳ
c t đ ng tròn, đi m A thay đ i trên C(O,R). V hình bình hành ABCD. Tìm qu tích tr ng tâm Gắ ườ ể ổ ẽ ỹ ọ
c a tam giác BCD?ủ
––––––––––––––––––––H t–––––––––––––––––––ế
H và tên thí sinhọ: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SBD :. . . . . . . . . .
1
x
G
D
C
B
S
M
I
E
Q
N
P
S GD&ĐT QU NG NAMỞ Ả
TR NG THPT CAO BÁ QUÁTƯỜ
Đ s 6ề ố
ĐÁP ÁN Đ THI H C KÌ 1 – Năm h c 2010 – 2011Ề Ọ ọ
Môn TOÁN L p 11ớ
Th i gian làm bài 90 phútờ
TT N i dungộĐi mể
Câu 1
(2đi m)ểa. (0,5 đi m) PT ể
xsin2 sin( )
3
π
= −�
x k
x k k
6
2,
3
ππ
ππ Ζ
= − +
= +
0,25
0,25
b. (0,5 đi m) ể
pt x
x k k
0
0 0
cot( 15 ) 1
30 180 ,
Ζ
+ =�
= +� �
0,25
0,25
c. (1đi m) p tể⇔ 3sinx + 1 – sin2x – 3 = 0
⇔ sin2x – 3sinx + 2 = 0
x chon
x loai
sin 1 ( )
sin 2 ( )
=
=
x k k2 ,
2
ππ Ζ
= +� �
0,25
0,25
0,25
0,25
Câu 2
(2đi m)ểa. (1đi m)ể
a b C a C a b C a b C a b C ab C b
5 0 5 1 4 2 3 2 3 2 3 4 4 5 5
5 5 5 5 5 5
(2 ) (2 ) (2 ) (2 ) (2 ) 2+ = + + + + +
= 32a5 + 80a4b + 80a3b2 + 40a2b3 + 10ab4 + b5
H s c a aệ ố ủ 2b3 là 40
0,5
0,25
0,25
b. (1đi m)ể
Không gian m u ẫ
C5
14 2002Ω = =
ph n tầ ử
Bi n c A l y 3 qu c u xanh, 2 vàng có ế ố ấ ả ầ
n A C C
3 2
8 6
( ) . 56.15 840= = =
P(A) = 0,42
0,25
0,5
0,25
Câu 3
(3đi m)ểHình v cho câu a,b.ẽ
a. (0,5 đi m) ể
Ta có S ∈(SAB) ∩ (SCD)
và AB// CD , AB ⊂ (SAB),
CD ⊂ (SCD)
⇒ (SAB) ∩ (SCD) = Sx//AB
0,25
0,25
0,25
b. (1,25 đi m) (ểα) ∩ (SAD) = MN//SA
(α) ∩ (SCD) = NP//CD
(α) ∩ (ABCD) = MQ//CD
(α) ∩ (SBC) = PQ
→ Thi t di n là t giác MNPQ .ế ệ ứ
Vì NP//MQ//CD nên t giác MNPQ là hình thang.ứ
0,25
0,25
0,25
0,25
0,25
c. (1đi m) AG ể∩ Sx = E ; I là trung đi m c a ABể ủ
Ch ng minh MG// DEứ
DE
(SCD => MG // (SCD)
0.25
0.5
0,25
Câu 4a
(1đi m)ểB c 1: VT = VP = 2ướ
B c 2: Gi s MĐ đúng v i n = k .....ướ ả ử ớ 0,25
0,25
2
CM MĐ đúng v i n = k +1....ớ
= VP (đpcm)
KL
0,25
0,25
Câu 5a
(1đi m)ể G i Iọ’(x, y) là nh c a I qua Vả ủ (A,–2) ta có
AI AI' 2= −
uuur uur
x x
y y
3 4 7
1 6 7
� �
− = =
� �
� �
− = =
� �
R’ = –2.2= 4
V y (Cậ’): (x – 7)2 + (y –7)2 = 16
0,25
0,25
0,25
0,25
Câu 6a
(1đi m)ể sin3x + cos2x = 1 + 2sinxcos2x ⇔ sin3x – (1– cos2x) = sin3x – sinx
⇔ –2sin2x = – sinx
x
x
sin 0
1
sin 2
=
=
x k
x k k
x k
2 ;
6
52
6
π
ππ Ζ
ππ
=
= +� �
= +
0,25
0,25
0,25
0,25
Câu 4b 9sinx + 6cosx – 3sin2x + cos2x = 8
⇔ 9sinx + 6cosx – 6sinx.cosx + 1 – 2sin2x = 8
⇔ 6cosx(1 – sinx) – (2sin2x – 9sinx + 7) = 0
⇔ 6cosx(1 – sinx) – (sinx – 1)(2sinx – 7) = 0
⇔ (1–sinx)(6cosx + 2sinx – 7) = 0
0.25
0.25
⇔
x
x x VN
1 sin 0
6cos 2sin 7 0 ( )
− =
+ − =
0,25
⇔
x k2
2
ππ
= +
0,25
Câu 5b ĐK:
n n2;
ﾥ
( )
n n
n n n
n n
C C A n n n n
1 2 2
1
1821 1 821 1640 0 40
2 2
−−
+ + = + + = + − = =� � �
0,25
k k k k k
k k
x C x x C x
x
40 40 40
40 2 40 3
40 40
20 0
1− − −
= =
� �
+ = =
� �
� �
� �
0,25
k k40 3 31 3− = =�
0,25
V y h s c a ậ ệ ố ủ x31 là
C3
40 9880=
0,25
Câu 6b G i I là trung đi m c a BD,ọ ể ủ
IG IA
1
3
= −
uur uur
0.5
G là nh c a A qua phép v t tâm I t s ả ủ ị ự ỉ ố
k1
3
= −
0.25
K t lu n đ c qu tíchế ậ ượ ỹ 0.25
=================
3
I
O
B
D
C
A
G