S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ KI M TRA CH T L NG H C KỲ IỂ Ấ ƯỢ Ọ
Đ NG THÁPỒNăm h c: 2012-2013ọ
Môn thi: TOÁN - L p 10ớ
Th i gian: 90 phút (ờkhông k th i gian phát để ờ ề)
Ngày thi: /12/2012
Đ Đ XU TỀ Ề Ấ
(Đ g m có 01 trang)ề ồ
Đ n v ra đ : THPT Long Khánh Aơ ị ề
I. PH N CHUNG CHO T T C THÍ SINH (7.0 đi m)Ầ Ấ Ả ể
Câu I (1.0 đi m)ể
Cho hai t p h p ậ ợ
[
)
4;8A
= −
và
(2;10)B
=
. Tìm các t p h p ậ ợ
, \A B A B
Câu II (2.0 đi m)ể
1) L p b ng bi n thiên và v đ th hàm s ậ ả ế ẽ ồ ị ố
2
2 2y x x= − +
2) Tìm Parabol y = ax2 - 4x + c, bi t r ng Parabol đó có tr c đ i x ng là đ ng th ngế ằ ụ ố ứ ườ ẳ
x = 2 và c t tr c hoành t i đi m M(3; 0)ắ ụ ạ ể
Câu III (2.0 đi m)ể
1) Giai ph ng trinh ươ
2 1 2x x− = −
2) Gi i ph ng trinh ả ươ
3 1 9 1x x x+ − = + −
Câu IV (2.0 đi m)ể
Trong măt phăng toa đô Oxy cho tam giác ABC có A( 2; 3 ), B( -1; -1) và
(0;6)C
a) Tính chu vi c a tam giác ABCủ
b) Tìm toa đô đ nh D đê ABDC la hinh binh hanh. ỉ
II. PH N RIÊNG-PH N T CH N (3.0 đi m)Ầ Ầ Ự Ọ ể
Thí sinh ch đ c làm m t trong hai ph n (ph n 1 ho c ph n 2)ỉ ượ ộ ầ ầ ặ ầ
Ph n 1: Theo ch ng trình chu nầ ươ ẩ
Câu V.a (2.0 đi m)ể
1) Không s d ng máy tính b túi, hãy gi i h ph ng trình ử ụ ỏ ả ệ ươ
3 2 8
4 3 5
x y
x y
+ =
− + = −
2) Tìm giá tr nh nh t c a hàm s ị ỏ ấ ủ ố
v i ớ
4x
>
Câu VI.a (1.0 đi m)ể
Cho tam giác ABC vuông t i A có AC = 10 và AB = 22. Tính tích vô h ng ạ ướ
.CA CB
uuur uuur
.
Ph n 2: Theo ch ng nâng caoầ ươ
Câu V.b (2.0 đi m)ể
1) Gi i h ph ng trình ả ệ ươ
2 2
7
10
x y xy
x y
+ + =
+ =
2) Tìm m đ ph ng trình ể ươ
2
3( 1) 3 12 0x m x m+ − + − =
có hai nghi m trái d u.ệ ấ
Câu VI.b (1.0 đi m)ể
Cho tam giác ABC vuông t i A có AC = 10 và AB = 22. Tính tích vô h ng ạ ướ
.CA CB
uuur uuur
.
H TẾ
4
2
O
1
2
1
y
x
x = 1
A
I
B
S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ KI M TRA CH T L NG H C KÌ IỂ Ấ ƯỢ Ọ
Đ NG THÁPỒNăm h c: 2012-2013ọ
Môn thi: TOÁN – L p 10ớ
H NG D N CH M Đ Đ XU TƯỚ Ẫ Ấ Ề Ề Ấ
(H ng d n ch m g m có 04 trang)ướ ẫ ấ ồ
Đ n v ra đ : THPT Long Khánh Aơ ị ề
Câu Ý N i dung yêu c uộ ầ Đi mể
I. PH N CHUNG CHO T T C THÍ SINHẦ Ấ Ả 7,00
Câu I
(2,0 đ) Cho hai t p h p ậ ợ
[
)
4;8A
= −
và
(2;10)B
=
. Tìm các t p h pậ ợ
, \A B A B
1,00
=� (2;8)A B
0,50
[ ]
\ 4;2A B = −
0,50
Câu II
(2,0 đ)
2,00
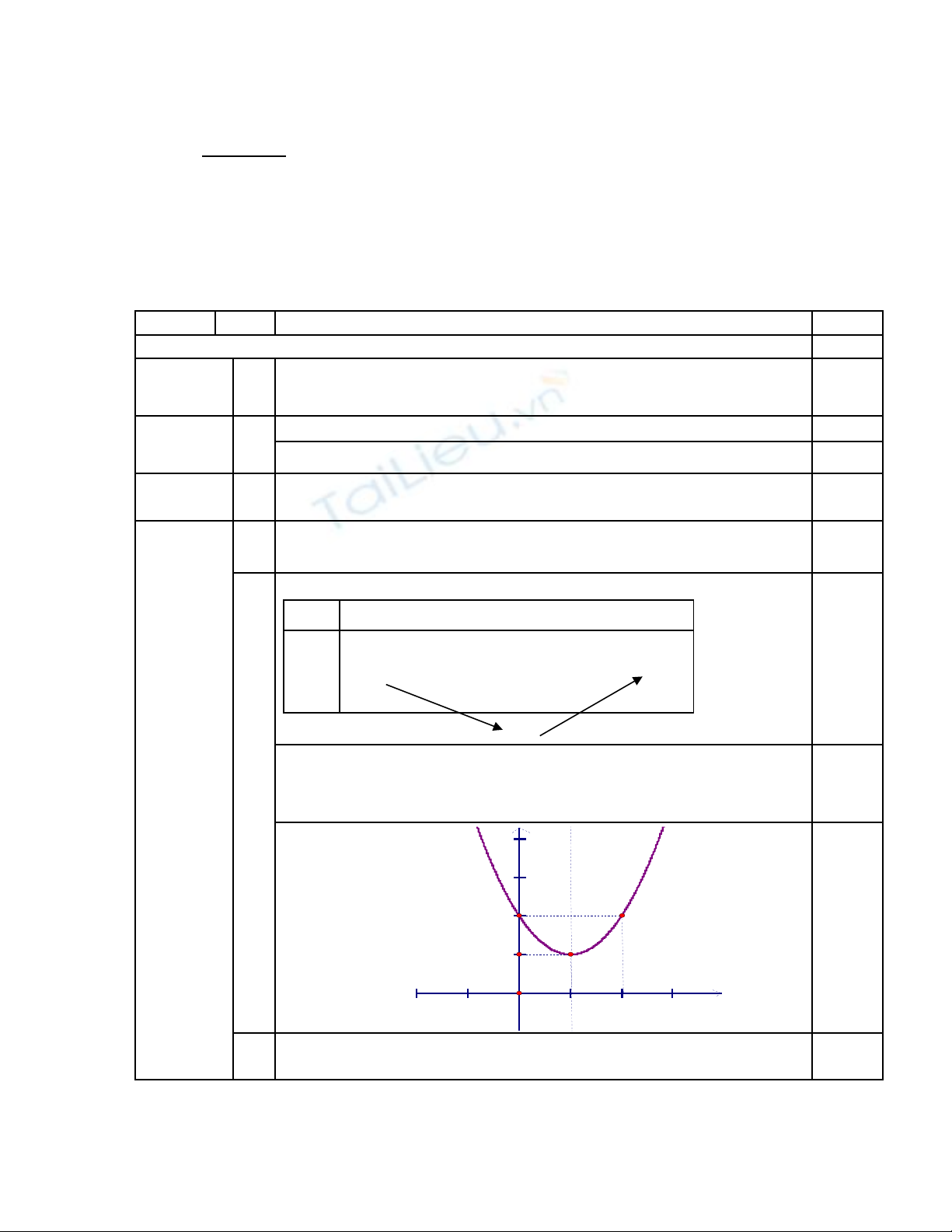
1L p b ng bi n thiên và v đ th hàm s ậ ả ế ẽ ồ ị ố
2
2 2y x x= − +
0,25
V i a = 1>0 ta có b ng bi n thiên:ớ ả ế 0,25
0,25
Parabol có đ nh: ỉ
( )
1;1I
, tr c đ i x ng: ụ ố ứ
=1x
và các đi m đ cể ặ
bi t ệ
0,25
Đ th :ồ ị 0,25
2Tìm Parabol y = ax2 - 4x + c, bi t r ng Parabol đó có tr c đ iế ằ ụ ố
x ng là đ ng th ng x = 2 và c t tr c hoành t i đi m M(3; 0)ứ ườ ẳ ắ ụ ạ ể 1,00
x
−
1
+
y
+
+
1
Tr c đ i x ng ụ ố ứ
2 2
2
b
xa
−
= =�
(
0a
)
42
2a=�
1a
=�
0,25
0,25
M t khác parabol c t tr c hoành t i M(3;0) nên:ặ ắ ụ ạ
2
9 12 0a c− + =
2
12 9.1 3c= − =�
0,25
V y parabol c m tìm là ậ ầ
24 3y x x= − +
0,25
Câu III
(2,0 đ)
1Giai ph ng trinh ươ
2 1 2x x− = −
(1) 1,00
Đi u ki n ề ệ
1
2
x
0,25
Bình ph ng hai v c a ph ng trình (1) ta đ c ph ngươ ế ủ ươ ượ ươ
trình
2 2
2 1 4 4 6 5 0
5
1
x x x x x
x
x
− = − + − + =�
=
=
0,25
0,25
Th l i ta th y ph ng trình có nghi m x = 5ử ạ ấ ươ ệ 0,25
2Gi i ph ng trinh ả ươ
3 1 9 1x x x+ − = + −
(2) 1,00
Đi u ki n ề ệ
1x
0,25
(2) 3 9x=�
3x=�
(nh n)ậ0,25
0,25
V y ph ng trình có nghi m x = 3.ậ ươ ệ 0,25
Câu IV
(2,0 đ)
Trong măt phăng toa đô Oxy cho tam giác ABC có A( 2; 3 ), B(
-1; -1) và
(0;6)C
2,00
1Tính chu vi c a tam giác ABCủ1,00
Ta có
( 3; 4) 5AB AB= − − =�
uuur
0,25
(1;7) 5 2BC BC= =�
uuur
0,25
0,25
( 2;3) 13AC AC= − =�
uuur
0,25
Chu vi tam giác ABC là
5 5 2 13+ +
0,25
2Tìm toa đô đ nh D đê ABDC la hinh binh hanh ỉ .1,00
G i D(x;y) là đ nh c a hình bình hành ABDCọ ỉ ủ 0,25
Ta có
( 3; 4)AB = − −
uuur
;
( ; 6)CD x y= −
uuur
0,25
0,25
Vì ABDC la hinh binh hanh nên
AB CD=
uuur uuur
hay
3 3
6 4 2
x x
y y
= − = −
� �
� �
− = − =
� �
0,25
V y D(-3 ; 2) là đ nh c n tìm.ậ ỉ ầ 0,25
II. PH N RIÊNG-PH N T CH NẦ Ầ Ự Ọ
Ph n 1: Theo ch ng trình chu nầ ươ ẩ
Câu V.a
1Không s d ng máy tính b túi, hãy gi i h ph ng trìnhử ụ ỏ ả ệ ươ
3 2 8
4 3 5
x y
x y
+ =
− + = −
Ta có
3 2 8
4 3 5
x y
x y
+ =
− + = −
12 8 32
12 9 15
x y
x y
+ =
− + = −
1,00
0,5
17 17 2
12 9 15 1
y x
x y y
= =
� �
� �
� �
− + = − =
� �
0,25
V y h ph ng trình đã cho có nghi m là (2 ; 1)ậ ệ ươ ệ 0,25
2Tìm giá tr nh nh t c a hàm s ị ỏ ấ ủ ố
v i ớ
4x
>
1,00
Ta có
1 1
4 4
4 4
y x x
x x
= + = − + +
− −
0,25
Vì
4x
>
nên x – 4 > 0 và
10
4x>
−
0,25
Suy ra
6y
;
6 5y x= =�
0,25
V y giá tr nh nh t c a hàm s ậ ị ỏ ấ ủ ố
là 6 khi x = 5 0,25
Câu VI.a Cho tam giác ABC vuông t i A có AC = 10 và AB = 22. Tínhạ
tích vô h ng ướ
.CA CB
uuur uuur
1,00
Xét tam giác ABC vuông t i A, ta có ạ
cos AC
CBC
=
0,25
Khi đó
. | |.| |. os( , ) . .cosCA CB CA CB C CA CB AC BC C= =
uuur uuur uuur uuur uuur uuur
2
. . 100
AC
AC BC AC
BC
= = =
0,25
0,25
V y ậ
. 100CA CB =
uuur uuur
0,25
Ph n 2: Theo ch ng trình nâng caoầ ươ
Câu V.b
1Gi i h ph ng trình ả ệ ươ
2 2
7
10
x y xy
x y
+ + =
+ =
1,00
2 2
7
10
x y xy
x y
+ + =
+ =
2
7
( ) 2 10
x y xy
x y xy
+ + =
+ − =
(*) 0,25
Đ t ặ
;S x y P xy= + =
(đi u ki n ề ệ
24S P
), h (*) tr thành:ệ ở
2
74
3
2 10
S P S
P
S P
+ = =
� � =
− =
(nh n) ho c ậ ặ
6
13
S
P
= −
=
(lo i)ạ
0,25
Suy ra x, y là ngi m c a ph ng trình ệ ủ ươ
21
4 3 0 3
X
X X X
=
− + = =
0,25
V y h ph ng trình đã cho có nghi m là (1;3); (3;1)ậ ệ ươ ệ 0,25
2Tìm m đ ph ng trình ể ươ
23( 1) 3 12 0x m x m+ − + − =
có hai
nghi m trái d u.ệ ấ
1,00
Ph ng trình có hai nghi m trái d uươ ệ ấ
. 0a c
<�
0,25
3 12 0
4
m
m
− <�
<�
0,25
0,25
V y m < 4 thì ph ng trình có hai nghi m trái d uậ ươ ệ ấ 0,25
Câu VI.b Cho tam giác ABC vuông t i A có AC = 10 và AB = 22. Tínhạ
tích vô h ng ướ
.CA CB
uuur uuur
1,00
Xét tam giác ABC vuông t i A, ta có ạ
cos AC
CBC
=
0,25
Khi đó
. | |.| |. os( , ) . .cosCA CB CA CB C CA CB AC BC C= =
uuur uuur uuur uuur uuur uuur
2
. . 100
AC
AC BC AC
BC
= = =
0,25
0,25
V y ậ
. 100CA CB =
uuur uuur
0,25
L u ýư : 1) N u h c sinh không theo cách nêu trong đáp án nh ng đúng và h p logic thìế ọ ư ợ
cho đ s đi m t ng ph n nh h ng bdaaxn quy đ nhủ ố ể ừ ầ ư ướ ị
2) Các b c ph không có ho c sai thì không ch m b c k ti pướ ụ ặ ấ ướ ế ế