
PHÒNG GD & ĐT BÌNH S NƠ Đ THI CH N H C SINH GI I L P 8 C PỀ Ọ Ọ Ỏ Ớ Ấ
HUY NỆ
NĂM H C 2009 – 2010Ọ
MÔN TOÁN
Th i gian 150 phút (không k th i gian giao đ )ờ ể ờ ề
Bài 1: (4 đi m)ể
Phân tích các đa th c sau thành nhân t :ứ ử
a) (x + y + z) 3 – x3 – y3 – z3.
b) x4 + 2010x2 + 2009x + 2010.
Bài 2: (2 đi m)ể
Gi i ph ng trình:ả ươ
x 241 x 220 x 195 x 166 10
17 19 21 23
− − − −
+ + + =
.
Bài 3: (3 đi m)ể
Tìm x bi t:ế
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
2 2
2 2
2009 x 2009 x x 2010 x 2010 19
49
2009 x 2009 x x 2010 x 2010
− + − − + − =
− − − − + −
.
Bài 4: (3 đi m)ể
Tìm giá tr nh nh t c a bi u th c ị ỏ ấ ủ ể ứ
2
2010x 2680
Ax 1
+
=+
.
Bài 5: (4 đi m)ể
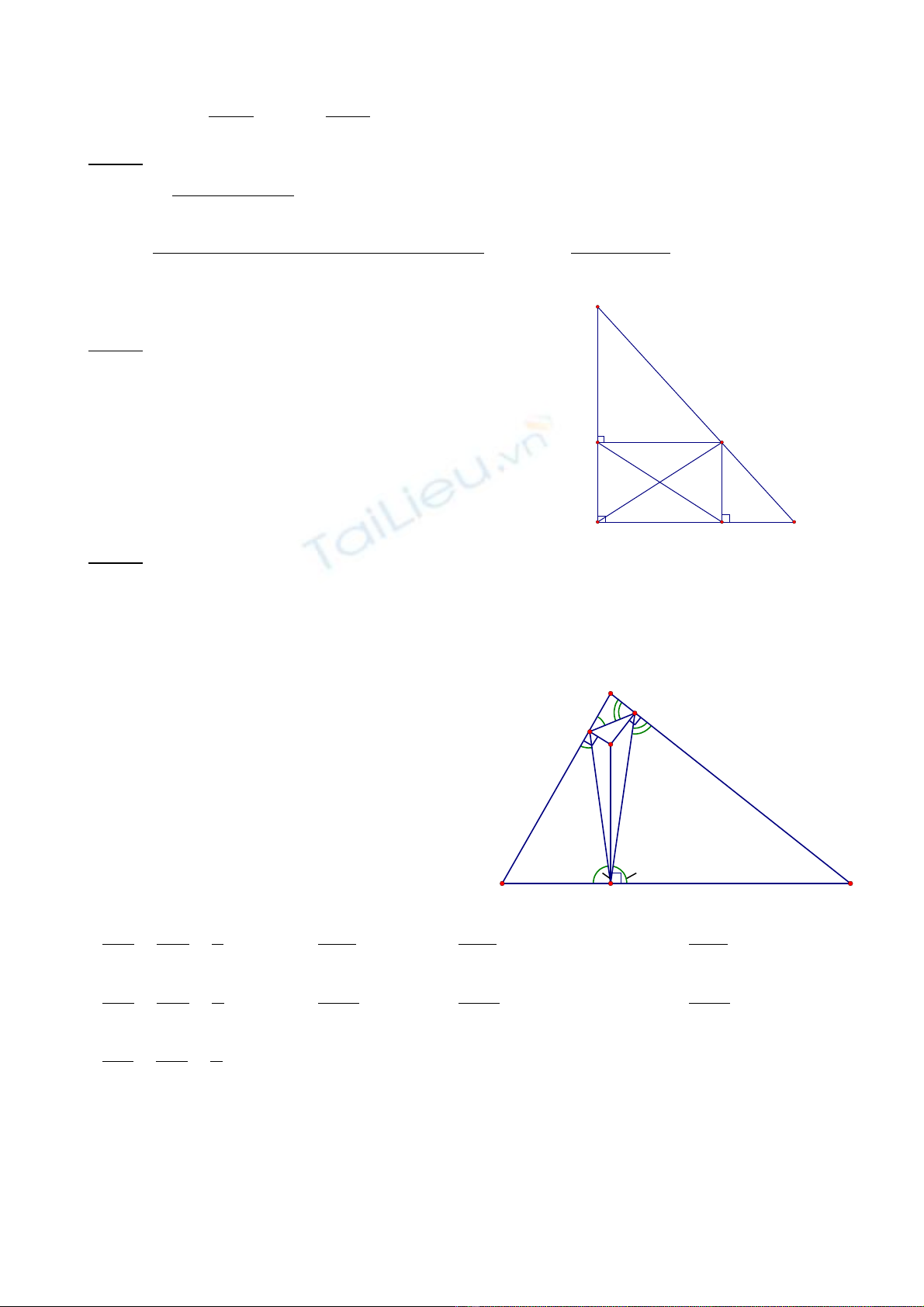
Cho tam giác ABC vuông t i A, D là đi m di đ ng trên c nh BC. G i E, F l nạ ể ộ ạ ọ ầ
l t là hình chi u vuông góc c a đi m D lên AB, AC.ượ ế ủ ể
a) Xác đ nh v trí c a đi m D đ t giác AEDF là hình vuông.ị ị ủ ể ể ứ
b) Xác đ nh v trí c a đi m D sao cho 3AD + 4EF đ t giá tr nh nh t.ị ị ủ ể ạ ị ỏ ấ
Bài 6: (4 đi m)ể
Trong tam giác ABC, các đi m A, E, F t ng ng n m trên các c nh BC, CA,ể ươ ứ ằ ạ
AB sao cho:
ᄋ
ᄋ
ᄋ
ᄋ
ᄋ
ᄋ
AFE BFD, BDF CDE, CED AEF= = =
.
a) Ch ng minh r ng: ứ ằ
ᄋ
ᄋ
BDF BAC=
.
b) Cho AB = 5, BC = 8, CA = 7. Tính đ dài đo n Bộ ạ D.

M t l i gi i:ộ ờ ả
Bài 1:
a) (x + y + z) 3 – x3 – y3 – z3 =
( )
33 3 3
x y z x y z
� � � �
+ + − − +
� �
� �
=
( ) ( ) ( ) ( )
( )
22 2 2
y z x y z x y z x x y z y yz z
� �
+ + + + + + + − + − +
� �
=
( )
( )
2
y z 3x 3xy 3yz 3zx+ + + +
= 3
( ) ( ) ( )
y z x x y z x y+ + + +
� �
� �
= 3
( ) ( ) ( )
x y y z z x+ + +
.
b) x4 + 2010x2 + 2009x + 2010 =
( ) ( )
4 2
x x 2010x 2010x 2010
− + + +
=
( )
( ) ( )
2 2
x x 1 x x 1 2010 x x 1
− + + + + +
=
( ) ( )
2 2
x x 1 x x 2010
+ + − +
.
Bài 2:
x 241 x 220 x 195 x 166 10
17 19 21 23
− − − −
+ + + =
x 241 x 220 x 195 x 166
1 2 3 4 0
17 19 21 23
− − − −
− + − + − + − =�
x 258 x 258 x 258 x 258 0
17 19 21 23
− − − −
+ + + =�
( )
1 1 1 1
x 258 0
17 19 21 23
� �
− + + + =�� �
� �
x 258=�
Bài 3:
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
2 2
2 2
2009 x 2009 x x 2010 x 2010 19
49
2009 x 2009 x x 2010 x 2010
− + − − + − =
− − − − + −
.
ĐKXĐ:
x 2009; x 2010
.
Đ t a = x – 2010 ặ(a
0), ta có h th c:ệ ứ
( ) ( )
( ) ( )
22
22
a 1 a 1 a a 19
49
a 1 a 1 a a
+ − + + =
+ + + +
2
2
a a 1 19
3a 3a 1 49
+ + =�+ +
2 2
49a 49a 49 57a 57a 19+ + = + +�
2
8a 8a 30 0+ − =�
( ) ( ) ( )
22
2a 1 4 0 2a 3 2a 5 0+ − = − + =� �
3
a2
5
a2
=
= −
(tho ĐK)ả
Suy ra x =
4023
2
ho c x = ặ
4015
2
(tho ĐK)ả
V y x =ậ
4023
2
và x =
4015
2
là giá tr c n tìm.ị ầ
Bài 4:
2
2010x 2680
Ax 1
+
=+
=
2 2 2
2 2
335x 335 335x 2010x 3015 335(x 3)
335 335
x 1 x 1
− − + + + +
= − + −
+ +
V y giá tr nh nh t c a A là – 335 khi x = – 3.ậ ị ỏ ấ ủ
Bài 5:
a) T giác AEDF là hình ch nh t (vì ứ ữ ậ
ᄋ
ᄋ
$
o
E A F 90= = =
)
Đ t giác AEDF là hình vuông thì AD là tia phân ể ứ
giác c a ủ
ᄋ
BAC
.
b) Do t giác AEDF là hình ch nh t nên AD = EFứ ữ ậ
Suy ra 3AD + 4EF = 7AD
3AD + 4EF nh nh t ỏ ấ
AD nh nh tỏ ấ
D là hình chi u vuông góc c a A lên BC.ế ủ
Bài 6:
a) Đ t ặ
ᄋ
ᄋ
ᄋ
ᄋ
ᄋ
ᄋ
AFE BFD , BDF CDE , CED AEF= = ω = = α = = β
.
Ta có
ᄋ
0
BAC 180+ β + ω =
(*)
Qua D, E, F l n l t k các đ ng th ng vuông góc v i BC, AC, AB c t nhauầ ượ ẻ ườ ẳ ớ ắ
t i O. Suy ra O là giao đi m ba đ ng phân giác c a tam giác DEF.ạ ể ườ ủ
ᄋ
ᄋ
ᄋ
o
OFD OED ODF 90+ + =
(1)
Ta có
ᄋ
ᄋ
ᄋ
o
OFD OED ODF 270+ ω+ +β + + α =
(2)
(1) & (2)
o
180α + β + ω =
(**)
(*) & (**)
ᄋ
ᄋ
BAC BDF= α =
.
b) Ch ng minh t ng t câu a) ta có:ứ ươ ự
ᄋ
B= β
,
ᄋ
C= ω
AEF
∆
DBF
∆
DEC∆
ABC∆
BD BA 5 5BF 5BF 5BF
BD BD BD
BF BC 8 8 8 8
CD CA 7 7CE 7CE 7CE
CD CD CD
CE CB 8 8 8 8
AE AB 5 7AE 5AF 7(7 CE) 5(5 BF) 7CE 5BF 24
AF AC 7
� � � �
= = = = =
� � � �
� � � �
� � � �
= = = = =� � �
� � � �
� � � �
= − = − − =
� � � �
= =
� � � �
� � � �
CD BD 3− =�
(3)
Ta l i có CD + BD = 8 (4)ạ
(3) & (4)
BD = 2,5
E
F
A
B
C
D
O
A
B
C
F
D
E
α
β
ω
β
ω
α
s
s
s






















![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



