Đề thi đề xuất: Kiểm tra Học kỳ I - năm học 2009-2010 - môn Toán lớp 12
----------------------------------------------------------------------------------------------------------------------------------------------------
----------------------------------------------------------------------------------------------------------------------------------------------------
Thầy giáo Nguyễn Văn Thiết - Trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 1
Trường THPT Vinh Xuân KIỂM TRA HỌC KỲ I - NĂM HỌC 2009-2010
Tổ Toán Tin MÔN TOÁN LỚP 12 ( Thời gian 90 phút )
----------- HƯỚNG DẪN CHẤM VÀ THANG ĐIỂM
A- PHẦN CHUNG ( 7 điểm )
Câu Nội dung Điểm
1.1 Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số 4 2
4 3
y x x
2,00
TXĐ:
D
¡
3 2
y x x x x
,
0 (0) 3
0
2 2 7
x y
yx y
+ Hàm số đồng biến trên các khoảng
2;0
và
2;

.
Hàm số nghịch biến trên các khoảng
; 2
 và
0; 2
.
+ Cực trị: Hàm số đạt cực đại tại điểm
0, 3
CD
x y
.
Hàm số đạt cực tiểu tại hai điểm
2
x
và
2
x;
7
CT
y
.
+ Giới hạn: lim
xy


Bảng biến thiên:
x

2
0
2

y
0
0
0
y

3

7
7
+ Đồ thị:
Đồ thị nhận trục tung làm trục đ
ối xứng .
0,25
0,25
0,25
0,25
0,50
0,50
1.2 Viết pt tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2 1,00
Với 0 0
2 3
x y
, suy ra điểm
2; 3 ( )
M C
.
Hệ số góc của tiếp tuyến của đồ thị (C) tại điểm M là:
(2) 16
k y
Phương trình tiếp tuyến tại M là:
16 2 3
y x
16 35
y x
.
0,25
0,25
0,50
Đề thi đề xuất: Kiểm tra Học kỳ I - năm học 2009-2010 - môn Toán lớp 12
----------------------------------------------------------------------------------------------------------------------------------------------------
----------------------------------------------------------------------------------------------------------------------------------------------------
Thầy giáo Nguyễn Văn Thiết - Trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 2
1.3 Dựa vào đồ thị (C) hãy biện luận theo m số nghiệm của phương trình... 1,00
Ta có phương trình: 4 2
4 0
x x m
(*) 4 2
4 3 3
x x m
Số nghiệm của phương trình (*) bằng số giao điểm của đồ thị (C) của hàm
số 4 2
4 3
y x x
và đường thẳng
3
y m
.
Dựa vào đồ thị ta có:
+
3 7 4
m m
: phương trình (*) vô nghiệm .
+
3 7 4
m m
: phương trình (*) có 2 nghiệm .
+
7 3 3 4 0
m m
: phương trình (*) có 4 nghiệm .
+
3 3 0
m m
: phương trình (*) có 3 nghiệm .
+
3 3 0
m m
: phương trình (*) có 2 nghiệm .
0,25
0,25
0,50
2.1 Giải phương trình
4.9 12 3.16 0
x x x
. 1,00
Ptr 2 2
4.3 3 .4 3.4 0
x x x x
2
3 3
4. 3 0
4 4
x x
Đặt
3
4
x
t
điều kiện
0
t
, phương trình trở thành 2
4 3 0
t t
.
Giải phương trình ta được
1
t
hoặc
3
4
t
.
Đối chiếu với điều kiện
0
t
ta chọn
3
4
t
hay
3 3
4 4
x
1
x
.
Vậy phương trình đã cho có một nghiệm là
1
x
.
0,25
0,25
0,25
0,25
2.2 Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số
2
3
x
y x e
trên đoạn
0;2
. 1,00
Ta có
2
2 3
x
y x x e
.
2
1
0 2 3 0
3
x
y x x x
. Vì
0;2
x nên ta chọn
1
x
.
Tính
1 2
y e
,
0 3
y
,
2
2
y e
.
Vậy
2
0;2
max
y e
khi
2
x
,
0;2
min 2
y e
khi
1
x
.
0,25
0,25
0,25
0,25
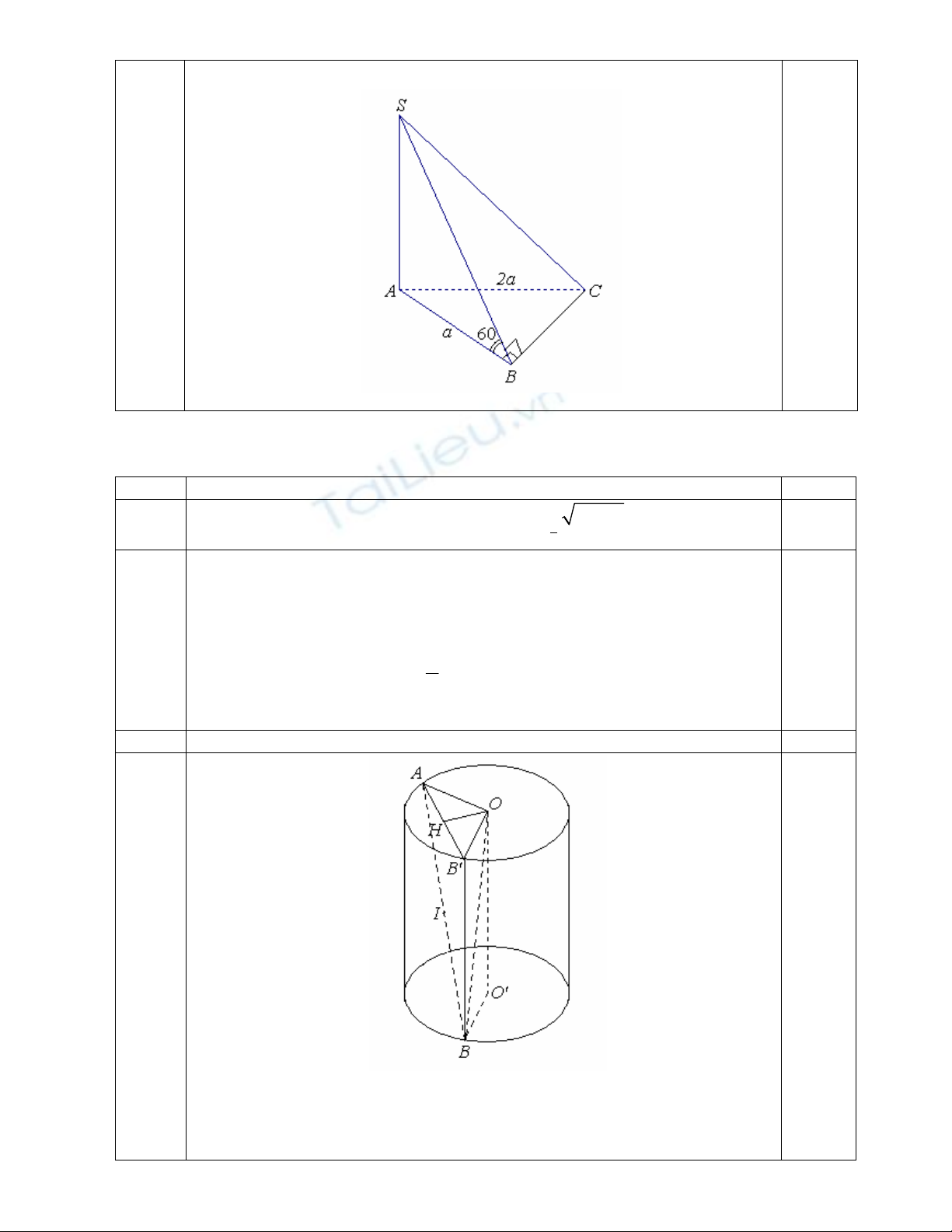
3 Tính thể tích khối chóp S.ABC theo a. 1,00
Vì hai mặt bên (SAB) và (SAC) cùng vuông góc với đáy (ABC) nên
( )
SA ABC
.
Suy ra góc giữa mặt bên (SBC) và đáy (ABC) là góc
·
0
60
SBA
.
Từ tam giác vuông SAB ta có 0
tan60 3
SA AB a
.
Từ tam giác vuông ABC ta có
2 2 2 2 2 2
4 3
BC AC AB a a a
3
BC a
.
Vậy thể tích khối chóp S.ABC là 1
.
3
ABC
V S SA
1 1 .
3 2
AB BC SA
1
. .
6
AB BC SA
3
1 1
. 3. 3
6 2
a a a a
.
0,25
0,25
0,25
Đề thi đề xuất: Kiểm tra Học kỳ I - năm học 2009-2010 - môn Toán lớp 12
----------------------------------------------------------------------------------------------------------------------------------------------------
----------------------------------------------------------------------------------------------------------------------------------------------------
Thầy giáo Nguyễn Văn Thiết - Trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 3
0,25
PHẦN RIÊNG ( 3 điểm )
* Phần 1: Theo chương trình chuẩn
Câu Nội dung Điểm
4a Giải bất phương trình:
21
8
log 2 2 6log 3 5
x x
1,00
Điều kiện 2 0
2
3 5 0
xx
x
.
Bpt
22
log 2 2 log 3 5
x x
2
log 2 3 5 2
x x
2
3 11 6 0
x x
2
3
3
x
.
Kết hợp với điều kiện, suy ra bpt có tập nghiệm
2;3
T.
0,25
0,25
0,25
0,25
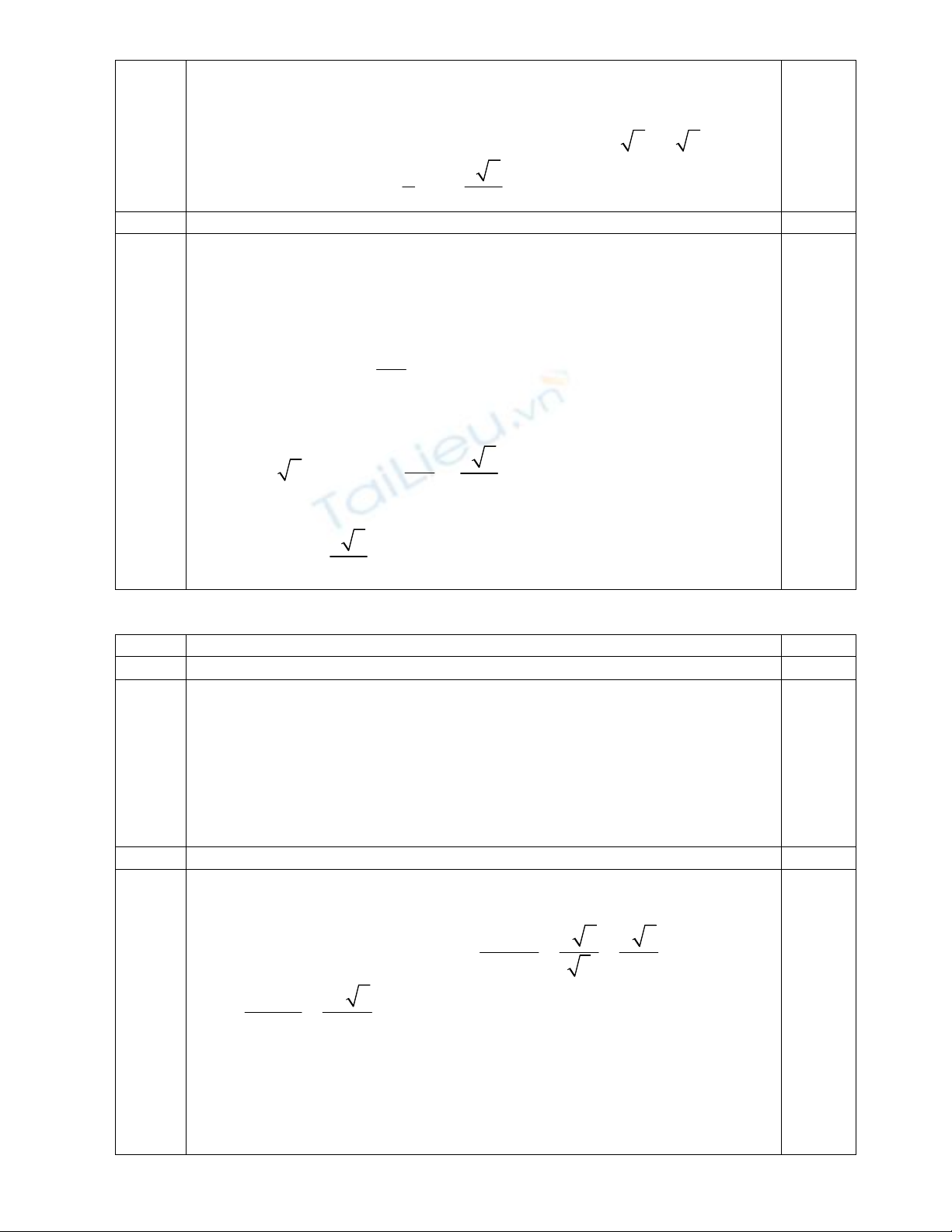
5a.1 Tính khoảng cách giữa đường thẳng AB và trục OO’ theo r. 1,00
Dựng đường sinh BB’, ta có
//
BB OO
( )//
ABB OO
Gọi H là trung điểm của dây AB’ thì
OH AB
, đồng thời
OH BB
nên
( )
OH ABB
. Suy ra khoảng cách giữa AB và OO’ là
0,25
0,50
Đề thi đề xuất: Kiểm tra Học kỳ I - năm học 2009-2010 - môn Toán lớp 12
----------------------------------------------------------------------------------------------------------------------------------------------------
----------------------------------------------------------------------------------------------------------------------------------------------------
Thầy giáo Nguyễn Văn Thiết - Trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 4
, ( ),
d AB OO d ABB OO
( ),
d ABB O OH
.
Theo giả thiết ta có
·
0
, , 90
AOB OA OB OA O B
.
Do đó tam giác OAB’ vuông cân tại O, suy ra
2 2
AB OA r
.
Vậy
1 2
,
2 2
r
d AB OO OH AB
.
0,25
5a.2 Tính diện tích mặt cầu ngoại tiếp tứ diện OO’AB theo r. 1,00
Theo giả thiết ta có
OA O B
và
OA OO
suy ra
( )
OA OBO
OA OB
·
0
90
AOB
.
Chứng minh tương tự ta được
·
0
90
AO B
.
Suy ra hai điểm O và O’ cùng nằm trên mặt cầu đường kính AB hay mặt
cầu tâm I bán kính
2
AB
R ngoại tiếp tứ diện OO’AB ( với I là trung điểm
của AB ).
Từ tam giác vuông ABB’ ta có
2 2 2
AB AB BB
2 2 2
2 4 6
r r r

6
AB r
. Suy ra
2
AB
R
6
2
r
.
Vậy diện tích mặt cầu ngoại tiếp tứ diện OO’AB là
2
2
6
4 4 2
r
S R
2
6
r
.
0,25
0,25
0,25
0,25
* Phần 2: Theo chương trình nâng cao
Câu Nội dung Điểm
4b Giải hệ phương trình 1,00
Điều kiện
0
x y
và
0
x
.
Hpt
4
2
2 2 2
2
log log log 9
3 3
x y
x y x
2
9
2 4
x y x
x y
2
4 2 9
4 2
x x x
y x
2
17 16 0
4 2
x x
y x
1
2
x
y
hoặc
16
28
x
y
0,25
0,25
0,50
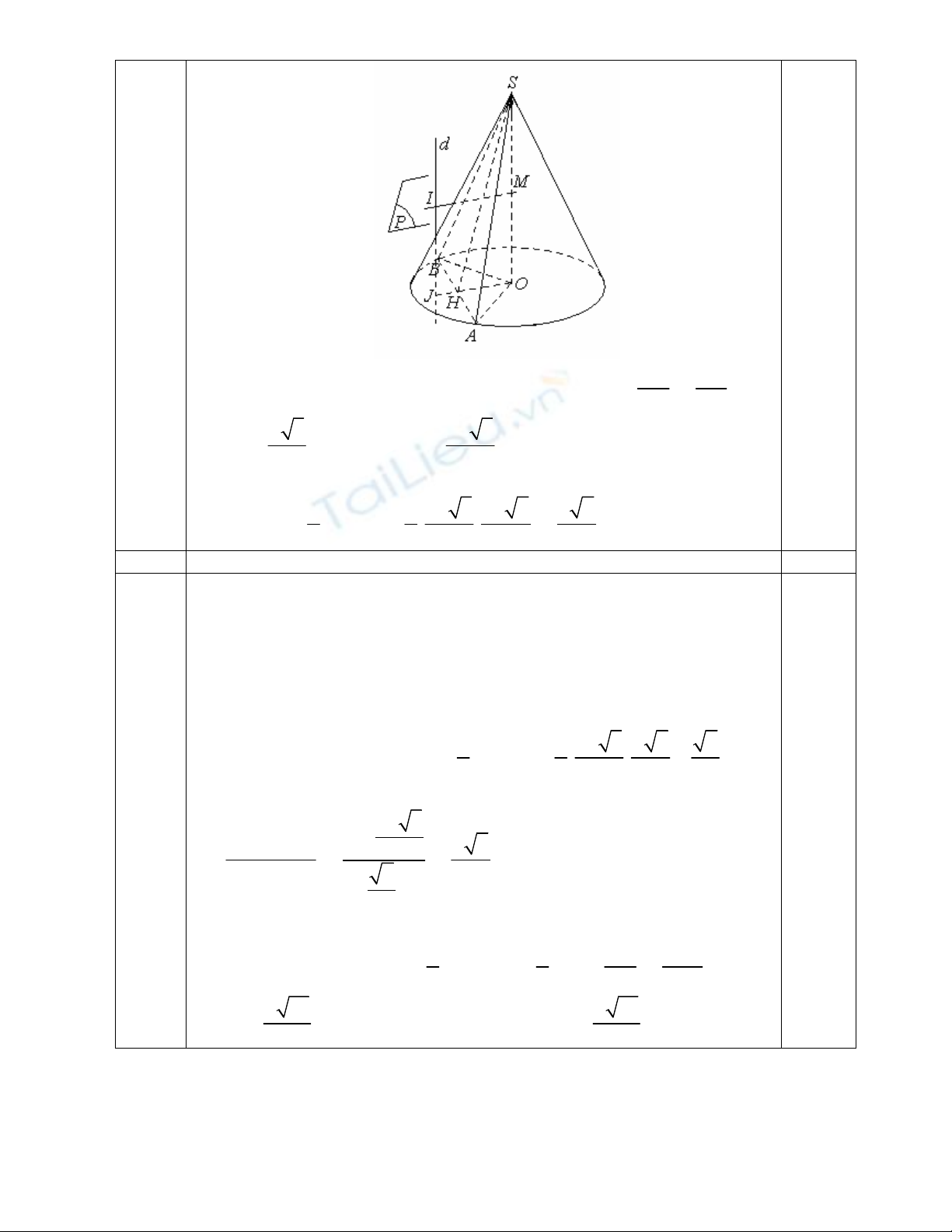
5b.1 Tính diện tích tam giác SAB theo a . 1,00
Gọi H là trung điểm của dây AB thì
OH AB
SH AB
( định lý ba
đường vuông góc )
·
0
60
SHO
là góc giữa (SAB) và đáy.
Từ tam giác vuông SHO ta có 0
2 6
tan60 3
3
SO a a
OH ,
0
2 6
sin60 3
SO a
SH
0,25
Đề thi đề xuất: Kiểm tra Học kỳ I - năm học 2009-2010 - môn Toán lớp 12
----------------------------------------------------------------------------------------------------------------------------------------------------
----------------------------------------------------------------------------------------------------------------------------------------------------
Thầy giáo Nguyễn Văn Thiết - Trường THPT Vinh Xuân, Phú Vang, Thừa Thiên Huế 5
Từ tam giác vuông OHA ta có
2
2 2 2 2
6
9
a
HA OA OH a
2
3
9
a
3
3
a
HA
2 3
2
3
a
AB HA .
Diện tích tam giác SAB là:
1 1 2 3 2 6
. . . .
2 2 3 3
SAB
a a
S AB SH
2
2 2
3
a
0,25
0,25
0,25
5b.2 Tính bán kính mặt cầu ngoại tiếp tứ diện OSAB theo a. 1,00
Gọi J là tâm đường tròn ngoại tiếp tam giác OAB. Vì tam giác OAB cân tại
O nên J nằm trên đường cao OH của tam giác đó.
Dựng đường thẳng d vuông góc với (OAB) tại J thì d là trục của đường tròn
ngoại tiếp tam giác OAB.
Dựng mặt phẳng trung trực (P) của cạnh bên SO cắt đường thẳng d tại I.
Khi đó I là tâm mặt cầu ngoại tiếp tứ diện OSAB, bán kính mặt cầu là
R IO
.
Diện tích tam giác OAB là
1 1 2 3 6
. . .
2 2 3 3
OAB
a a
S AB OH
2
2
3
a
Bán kính đường tròn ngoại tiếp tam giác OAB là
. .
4OAB
OAOB AB
rS
2
2 3
. .
3
2
4.
3
a
a a
a
6
4
a
.
Gọi M là trung điểm của cạnh bên SO, khi đó IMOJ là hình chữ nhật, suy ra
2 2 2 2
IO JM OM OJ
2 2
1
4
SO r
2
2
1 6
.2
4 16
a
a
2
14
16
a
14
4
a
IO . Vậy bán kính mặt cầu là
R IO
14
4
a
.
0,50
0,50