PHÒNG GD&ĐT
THÀNH PHỐ TAM KỲ
=========
ĐỀ KIỂM TRA CUỐI HỌC KÌ II – NĂM HỌC 2022-2023
MÔN: TOÁN - LỚP: 7
Thời gian: 60 phút (không kể thời gian giao đề)
ĐỀ CHÍNH THỨC
A. TRẮC NGHIỆM KHÁCH QUAN: (4,0 điểm): Chọn đáp án đúng ở mỗi câu sau
Câu 1: (NB) Cho
ac
=
bd
(a, b, c, d ≠0). Khẳng định nào sau đây không đúng?
A. 𝑎
𝑐=𝑏
𝑑
B. a.d = b.c.
C. a.b = c.d.
D. 𝑐
𝑎=𝑑
𝑏
Câu 2: (NB) Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ 3 được liên hệ với
nhau bởi công thức
A. y = -3x. B. y = 3x. C. y = 3
𝑥. D. 𝑦 = −3
𝑥.
Câu 3: (NB) Với điều kiện các phân thức đều có nghĩa thì:
A. 𝑎
𝑐=𝑏
𝑑=𝑎+𝑏
𝑐+𝑑 B. 𝑎
𝑐=𝑏
𝑑=𝑎+𝑏
𝑐−𝑑 C. 𝑎
𝑐=𝑏
𝑑=𝑎−𝑏
𝑐+𝑑 D.𝑎
𝑐=𝑏
𝑑=−𝑎+𝑏
𝑐+𝑑 .
Câu 4: (NB) Trong các biểu thức sau, biểu thức chứa số là:
A. 3
𝑥+ 3. B. 3a + 3. C. (2x+2):3. D. 24 + 2.4.
Câu 5: (NB) Đa thức nào dưới đây là đa thức một biến?
A. x3 – 2z2. B. 𝑥2 - 𝑥 + 3. C. x3 – 2y2 + 3. D. y3 - 2x2 + 3.
Câu 6: (NB) Đơn thức 2𝑥3 có bậc là:
A. 4. B. 1. C. 3. D. 2.
Câu 7: (NB) Đa thức 𝑓(𝑥)= 2𝑥 + 3. Giá trị 𝑓(1)= ?
A. 2 B. 3 C. 4 D. 5
Câu 8: (NB) Cho ΔMNP có 𝑀
< 𝑁
< 𝑃
. Khẳng định nào sau đây là đúng?
A. MN < MP < NP. B. NP < MP < MN.
C. MN > MP > NP. D. MP < NP < MN.
Câu 9: (NB) Cho ΔABC. Khẳng định nào sau đây là không đúng?
A. AB - AC > BC
B. AB + BC > AC
C. BC – AB < AC
D. BC < AC + AB
Câu 10: (NB) Hình lập phương có mấy mặt bên?
A. 8 mặt.
C. 4 mặt.
D. 6 mặt.
Câu 11: (NB) Hình hộp chữ nhật có:
A. 8 mặt, 6 đỉnh, 12 cạnh B. 6 mặt, 12 đỉnh, 8 cạnh
C. 12 mặt, 8 đỉnh, 6 cạnh D. 6 mặt, 8 đỉnh, 12 cạnh
Câu 12: (NB) Mỗi hình lăng trụ đứng tam giác có bao nhiêu đỉnh?
A. 2 đỉnh.
B. 3 đỉnh.
C. 4 đỉnh.
D. 6 đỉnh.
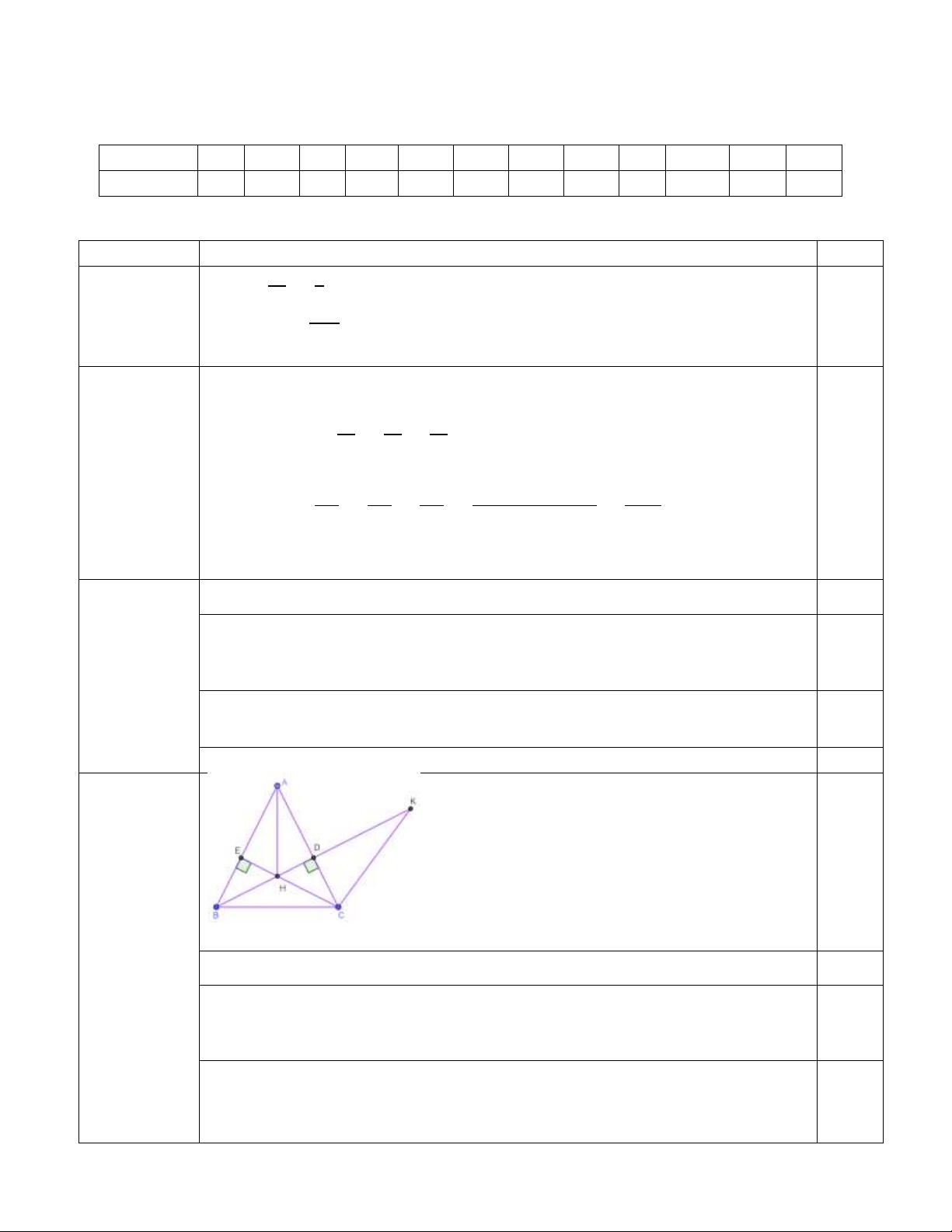
F
E
D
C
B
A
B. TỰ LUẬN: (6,0 điểm)
Câu 1: (TH) (0,5 điểm)
Tìm x trong tỉ lệ thức sau: 𝑥
15 =4
5
Câu 2 (VD) (1 điểm) Chia số 635 thành ba phần tỉ lệ thuận với 40; 42; 45.
Câu 3. (2 điểm) Cho đa thức A = 2𝑥2+ 8𝑥3− 7 + 𝑥
a) (TH) Sắp xếp đa thức A theo lũy thừa giảm dần của biến.
b) (TH) Xác định bậc; hệ số cao nhất; hệ số tự do của đa thức A
c) (VDC) Tìm a để đa thức 3𝑥3+ 2𝑥2− 3𝑥 + 𝑎 chia hết cho đa thức x – 1.
Câu 3: (2,5 điểm)
Cho
ABC cân tại A (𝐴
󰆹<900), vẽ BD ⊥ AC, CE ⊥ AB. Gọi H là giao điểm của
BD và CE.
a) (TH) Chứng minh:
ABD =
ACE.
b) (VD) Chứng minh AH là đường trung trực của ED.
c) (VDC) Trên tia đối của tia DB lấy điểm K sao cho DK = DB. Chứng minh
𝐸𝐶𝐵
= 𝐷𝐾𝐶
.
---------------Hết-------------
Người ra đề Hiệu trưởng
HƯỚNG DẪN CHẤM
A. TRẮC NGHIỆM: (4 điểm)
Mỗi câu trả lời đúng: 0,33điểm
Câu
1
2
3
4
5
6
7
8
9
10
11
12
Đáp án
C
B
A
D
B
C
D
B
A
C
D
D
B. TỰ LUẬN: (6điểm)
Câu
Đáp án
Điểm
Câu 1
(0,5 điểm)
Ta có: 𝑥
15 =4
5
𝑥 = 4.15
5
𝑥 = 12
0,5
Câu 2
(1 điểm)
Gọi x, y, z lần lượt là ba số cần tìm tỉ lệ thuận với 40; 42; 45
(0 < x; y; z < 635)
Theo đề ta có: 𝑥
40 =𝑦
42 =𝑧
45 và 𝑥 + 𝑦 + 𝑧 = 635
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
𝑥
40 =𝑦
42 =𝑧
45 =𝑥 + 𝑦 + 𝑧
40 +42 +45 =635
127 = 5
x = 40.5 = 200; y = 42.5 = 210; z = 45.5 = 225
Vậy 3 số cần tìm lần lượt là 200; 210; 225.
0,1
0,2
0,3
0,3
0,1
Câu 3
(2 điểm)
a) Sắp xếp: A = 8𝑥3+ 2𝑥2+ 𝑥 − 7.
0,75
b) Đa thức có bậc: 3
Hệ số cao nhất: 8
Hệ số tự do: -7
0,25
0,25
0,25
c) Thực hiện được phép chia:
3𝑥3+ 2𝑥2− 3𝑥 + 𝑎 = (x – 1).(
3𝑥2+ 5𝑥 + 2) + (𝑎 + 2)
0,3
Để chia hết a + 2 = 0 => a = - 2
0,2
Câu 3
(2,5 điểm)
Vẽ đúng hình
0,5
a)
ABD =
ACE ( ch - gn)
0,75
b)
AEH =
ADH (ch – cgv)
EH = DH và AE = AD
AH là đường trung trực của DE
0,5
0,25
c) Chứng minh 𝐷𝐵𝐶
= 𝐷𝐾𝐶
và 𝐷𝐵𝐶
= 𝐻𝐶𝐵
𝐸𝐶𝐵
= 𝐷𝐾𝐶
-
0,2
0,2
0,1
(Học sinh làm cách khác đúng vẫn cho điểm tối đa)