UBND QUẬN BÌNH THẠNH
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
THCS BÌNH LỢI TRUNG
ĐỀ ĐỀ NGHỊ
HỌC KỲ 2 NĂM HỌC 2024 – 2025
MÔN TOÁN LỚP 8
Thời gian 90 phút (Không kể thời gian phát đề)
I. TRẮC NGHIỆM KHÁCH QUAN: (3,0 ĐIỂM)
Câu 1: Trong các hàm số sau, hàm số nào là hàm số bậc nhất ?
1
.2Ay x
= −
. 34By x= −
2
.2Cyx= +
.1Dy x= +
Câu 2: Tọa độ giao điểm của đồ thị hàm số 𝑦𝑦=𝑓𝑓(𝑥𝑥)=𝑥𝑥+ 2 với đồ thị hàm số
𝑦𝑦=𝑓𝑓(𝑥𝑥)= 2𝑥𝑥 là:
A. (−2; −4) B. (−2; 4) C. (2; −4) D. (2; 4)
Câu 3: Đường thẳng d: 𝑦𝑦=−2𝑥𝑥+ 3 song song với đường thẳng nào sau đây?
A. d’: 𝑦𝑦=−2𝑥𝑥+ 1 B. d’: 𝑦𝑦=−2𝑥𝑥+ 3 C. d’: 𝑦𝑦= 2𝑥𝑥 − 3 D. d’: 𝑦𝑦= 3𝑥𝑥 − 2
Câu 4: Phương trình nào sau đây không phải là phương trình bậc nhất một ẩn
A.
+=
230
7
x
B.
− += 2
2 53xx
C.
D.
= +32xx
Câu 5: Nghiệm của phương trình 7𝑥𝑥– 1 = 6𝑥𝑥+ 3 là
A. 1 B. 2 C. 3 D. 4
Câu 6 : Xe thứ nhất đi nhanh hơn xe thứ hai 15km/h. Nếu gọi vận tốc xe thứ hai là x (km/h)
thì vận tốc xe thứ nhất là:
A. x – 15 (km/h) B. 15x (km/h) C. x + 15(km/h) D. 15 – x (km/h)
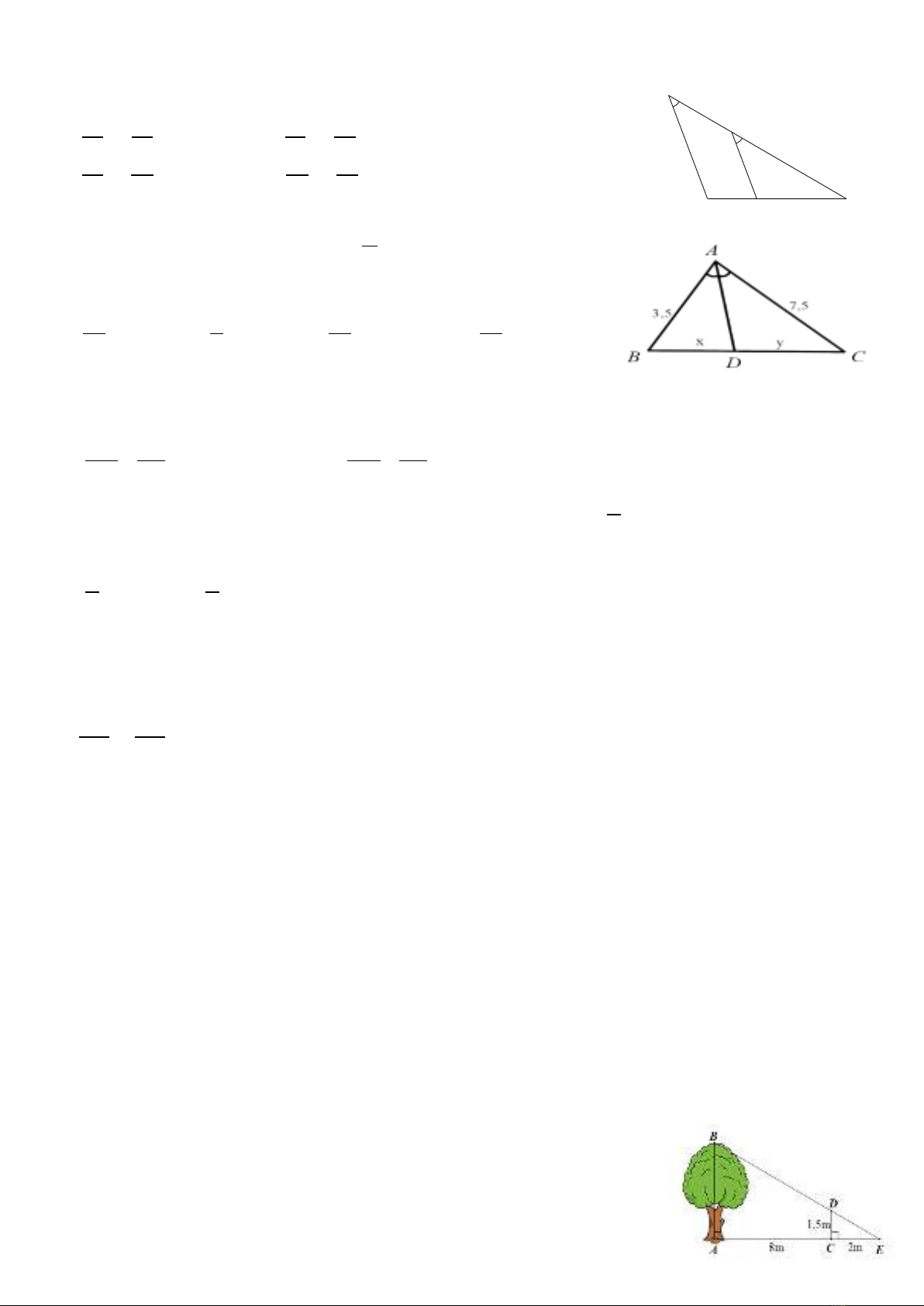
Câu 7: Trong hình sau đây, đường trung bình của tam giác ABC là ?
A. AF B. BE C. EF D. AD
Câu 8: Cho ∆ABC có MN // BC như hình vẽ. Theo định lý Thales, ta có:
A. MC
AC =AN
NB B. AM
MN =MN
BC C. AM
MB =AN
NC D. AM
MC =AN
NB
D
E
F
A
B
C
Câu 9 : Cho hình vẽ. Khẳng định nào sau đây KHÔNG đúng
A. CE
CD =CB
CA. B. BE
CB =AD
CA.
C. CE
BE =CD
AD. D. CD
DA =ED
AB
Câu 10: Hãy chọn câu đúng. Tỉ số
x
y
của các đoạn thẳng trong
hình vẽ, biết rằng các số trên hình cùng đơn vị đo là cm.
A.
7
15
B.
1
7
C.
15
7
D.
1
15
Câu 11 : Cho tam giác MNP đồng dạng với tam giác QRS, hãy chọn đáp án đúng:
A. B. C. 𝑀𝑀
�=𝑅𝑅
� D. 𝑁𝑁
�=𝑄𝑄
�
Câu 12: Nếu tam giác ABC đồng dạng với tam giác DEF theo tỉ số
1
2
thì tam giác DEF đồng dạng với
tam giác ABC theo tỉ số
11
. . . 2 .4
24
AB C D
II. TỰ LUẬN: (7,0 ĐIỂM)
Bài 1 (1,25 điểm) Giải phương trình
a) 3x – 4 = 7x + 20
b/ 𝑥𝑥+6
5−𝑥𝑥−2
3= 2
Bài 2 (1,5 điểm) Cho hai đường thẳng (d): y = 2x và (d’): y = x +1
a) Vẽ hai đường thẳng d và d’ trên cùng một mặt phẳng tọa độ Oxy.
b) Tìm tọa độ giao điểm của d và d’ bằng phép tính.
Bài 3 (1,0 điểm) Giải bài toán bằng cách lập phương trình bậc nhất
Một người đi xe máy từ A đến B với vận tốc là 45km/h. Đến B người đó làm việc hết 30
phút rồi quay về A với vận tốc 30km/h. Biết tổng thời gian là 4 giờ 30 phút. Hãy tính độ dài
quãng đường từ A đến B?
Bài 4 (2,5 điểm) Cho 𝜟𝜟ABC vuông tại A (AB < AC). Kẻ đường cao AH (H∈BC).
a) Chứng minh: 𝛥𝛥ABC ഗ 𝛥𝛥HAC và viết tỉ số đồng dạng
b) Lấy điểm M thuộc AH. Kẻ đường thẳng đi qua B và vuông góc với CM tại K. Chứng
minh: CM.CK = CH.CB
c) Tia BK cắt HA tại D. Chứng minh: 𝐵𝐵𝐵𝐵𝐵𝐵
�=𝐵𝐵𝐵𝐵𝐵𝐵
�
Bài 5 (0,75 điểm). Một người cắm một cái cọc vuông góc với mặt đất
sao cho bóng của đỉnh cọc trùng với bóng của ngọn cây (như hình vẽ).
Biết cọc cao 1,5 m so với mặt đất, chân cọc cách gốc cây 8 m và cách
bóng của đỉnh cọc 2 m. Tính chiều cao AB của cây?
MN NP
QR RS
=
MN NP
QR QS
=
E
D
A
B
C
ĐÁP ÁN
1. Trắc nghiệm (Mỗi câu đúng 0,25 điểm)
1 2 3 4 5 6 7 8 9 10 11 12
B D A B D C C D D A A C
2. Tự luận (7 điểm)
Câu
LỜI GIẢI
ĐIỂM
1a
0,5đ
Bài 1 (1,25 điểm) Giải phương trình
a/ 3x – 4 = 7x + 20
-4x = 24
x = -6
Vậy phương trình có nghiệm là x = -6
0,25x2
1b
0,75đ
𝑥𝑥+ 6
5−
𝑥𝑥 − 2
3= 2
3x+18 – 5x + 10 = 30
-2x = 2
x= -1
Vậy phương trình có nghiệm là x = -1
0,25x3
2a
1 đ
Bài 2 (1,5 điểm)
Cho hai đường thẳng (d): y = 2x và (d’): y = x + 1
a) Vẽ hai đường thẳng (d) và (d’) trên cùng một mặt phẳng tọa độ
Oxy.
Lập bảng giá trị
Vẽ 2 đường thẳng (d) và (d’)
0,25x2
0,25x2
2b
0,5 đ
b) Tìm tọa độ giao điểm của (d) và (d’) bằng phép tính.
Phương trình hoành độ giao điểm của (d ) và (d’) :
2x = x + 1
x = 1
suy ra : y= 2.1= 2
Vậy tọa độ giao điểm của (d), (d’) là : (1;2)
0,25
0,25
3
1 đ
Một người đi xe máy từ A đến B với vận tốc là 45km/h. Đến B
người đó làm việc hết 30 phút rồi quay về A với vận tốc 30km/h.
Biết tổng thời gian là 4 giờ 30 phút. Hãy tính độ dài quãng đường
từ A đến B?
Giải:
Đổi : 4 giờ 30 phút = 4,5 (h) , 30 phút = 0,5 (h)
Gọi x (km) là độ dài quãng đường AB ( x > 0)
Thời gian đi từ A đến B là 𝑥𝑥
45 (h)
Thời gian đi từ B đến A là 𝑥𝑥
30 (h)
Vì tổng thời gian là 4 giờ 30 phút nên ta có PT
𝑥𝑥
45
+𝑥𝑥
30
+ 0,5 = 4,5
0,25x4
75x = 5400
x=72 (thỏa điều kiện)
Vậy độ dài quãng đường AB là 72 km
4
2,5 đ
Cho 𝜟𝜟ABC vuông tại A (AB < AC). Kẻ đường cao AH (H∈BC).
d) Chứng minh: 𝛥𝛥ABC ഗ 𝛥𝛥HAC và viết tỉ số đồng dạng
e) Lấy điểm M thuộc AH. Kẻ đường thẳng đi qua B và
vuông góc với CM tại K. Chứng minh: CM.CK = CH.CB
f) Tia BK cắt HA tại D. Chứng minh: 𝐵𝐵𝐵𝐵𝐵𝐵
�=𝐵𝐵𝐵𝐵𝐵𝐵
�
a
Xét 𝛥𝛥ABC và 𝛥𝛥HAC có:
0
ˆˆ90 ( )
ˆ
A H gt
C chung
= =
Vậy 𝛥𝛥ABC ഗ 𝛥𝛥HAC (g-g)
Suy ra: 𝐴𝐴𝐴𝐴
𝐻𝐻𝐴𝐴
=𝐴𝐴𝐴𝐴
𝐻𝐻𝐴𝐴
=𝐴𝐴𝐴𝐴
𝐴𝐴𝐴𝐴
(𝑇𝑇𝑇𝑇Đ𝐵𝐵)
0,25x4
b
Chứng minh: 𝛥𝛥CMH
ഗ
𝛥𝛥CBK (g-g)
Suy ra: 𝐵𝐵𝑀𝑀
𝐵𝐵𝐵𝐵 =𝐵𝐵𝐵𝐵
𝐵𝐵𝐵𝐵 =𝑀𝑀𝐵𝐵
𝐵𝐵𝐵𝐵 (𝑇𝑇𝑇𝑇Đ𝐵𝐵)
Hay : CM. CK = CH. CB
0,25x3
c
Chứng minh: 𝛥𝛥BKC
ഗ
𝛥𝛥BHD (g-g)
Suy ra: 𝐵𝐵𝐵𝐵
𝐵𝐵𝐵𝐵 =𝐵𝐵𝐵𝐵
𝐵𝐵𝐵𝐵 (𝑇𝑇𝑇𝑇Đ𝐵𝐵)
Chứng minh: 𝛥𝛥BKH ഗ 𝛥𝛥BCD (c-g-c)
Suy ra : 𝐵𝐵𝐵𝐵𝐵𝐵
�=𝐵𝐵𝐵𝐵𝐵𝐵
�
0,25x3
5
0,75
đ
Một người cắm một cái cọc vuông góc với mặt đất sao cho bóng của
đỉnh cọc trùng với bóng của ngọn cây (như hình vẽ). Biết cọc cao 1,5 m
so với mặt đất, chân cọc cách gốc cây 8 m và cách bóng của đỉnh cọc 2
m. Tính chiều cao AB của cây?
A
B
H
M
K
C
D
Ta có : CD// AB ( cùng vuông góc AE)
2 1, 5
10
7,5( )
ECD EAB
EC CD
EA AB
hay AB
AB m
⇒∆ ∆
⇒=
=
=
Vậy chiều cao AB của cây là 7,5 m
0,25
0,25
0,25