MA TRẬN ĐỀ KIỂM TRA CUỐI KỲ II – TOÁN 9
A. BẢNG MA TRẬN ĐỀ KIỂM TRA.
T
T Chủ đề Nội dung/Đơn vị kiến thức
Mức độ đánh giá
Tổng số câu
Tổng
%
điểm
Nhận biết Thông hiểu Vận dụng Vận dụng cao
TNK
Q
T
L
TN
KQ
TL
TN
KQ
TL TNKQ TL
TNK
Q
TL
1
HÀM SỐ Y = ax2 ( a
≠0) VÀ PHƯƠNG
TRÌNH BẬC HAI
MỘT ẨN
Hàm số và đồ thị hàm số y = ax2
( a ≠ 0)
Phương trình bậc hai một ẩn
Định lí Vi1ète
5
2
(Bài
1a,b)
1
(Bài 2) 5 3 32,5
2 MỘT SỐ YẾU TỐ
THỐNG KÊ
Bảng tần số và biểu đồ tần số
Bảng tần số tương đối và biểu đồ
tần số tương đối
Biểu diễn số liệu ghép nhóm
2
2
( Bài
3a,b)
2 2 12,5
3
GIẢI TOÁN BẰNG
CÁCH LẬP
PHƯƠNG TRÌNH
Lập phương trình bậc hai một ẩn 1
1
( Bài
4)
1 1 10,0
4
TỨ GIÁC NỘI
TIẾP. ĐA GIÁC
ĐỀU
Đường tròn ngoại tiếp tam giác.
Đường tròn nội tiếp tam giác
Tứ giác nội tiếp
Đa giác đều và phép quay
2
1
(Bài
6a)
1
( Bài
6b)
1
(Bài
6c)
2 3 30,0
5
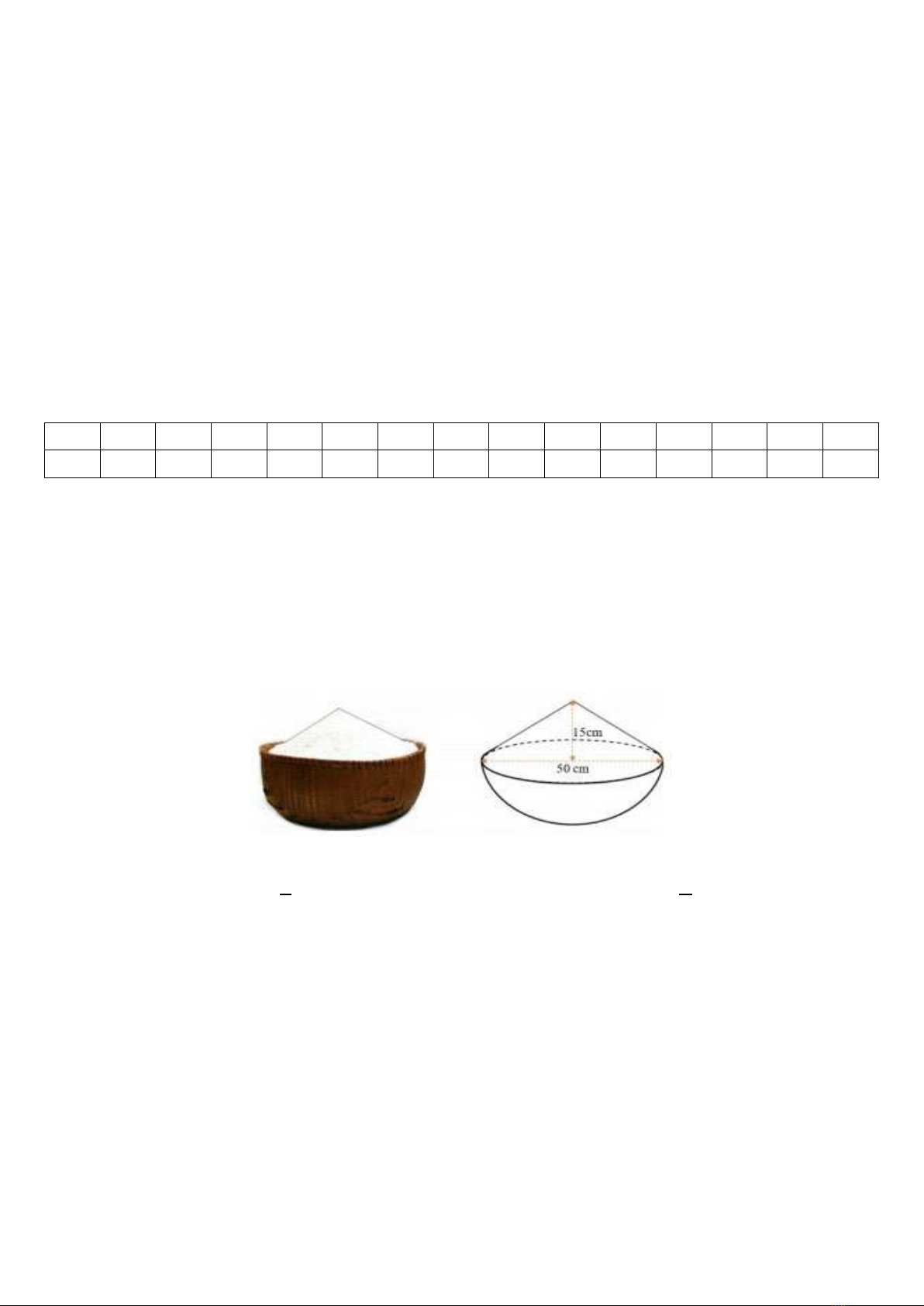
CÁC HÌNH KHỐI
TRONG THỰC
TIỄN
Hình Trụ
Hình nón
Hình cầu
2
2
( Bài
5a,b)
2 2 15,0
Tổng
12
6
4
1
12
12
Tỉ lệ %
30%
35%
25%
10%
100
Tỉ lệ chung
65%
35%
100