PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
CẨM GIÀNG
ĐỀ KHẢO SÁT CHẤT LƯỢNG THÁNG 4
NĂM HỌC 2023- 2024
MÔN: TOÁN - LỚP 9
Thời gian làm bài: 120 phút
(Đề gồm 01 trang)
Câu 1 (2,0 điểm).
1) Giải hệ phương trình:
23
21
xy
xy
2) Giải phương trình:
2
x 3x=
Câu 2 (2,0 điểm).
1) Rút gọn biểu thức: y =
2
x x 2x x x 1
1 .1
x x1 x x1
+ ++
+− +
−+ −
với
x 0, x 1>≠
2) Tìm m để hai đường thẳng (d1):
25yx= +
, (d2):
( 1) 2 1ym xm=++−
cắt nhau tại một
điểm có hoành độ là -1.
Câu 3 (2,0 điểm).
1) Sau hai năm dân số tỉnh A tăng từ 2 500 000 người lên 2 560 360 người. Hỏi tỉ lệ
tăng dân số hàng năm của tỉnh A là bao nhiêu phần trăm (biết trong hai năm tỉ lệ tăng dân
số không thay đổi)?
2) Cho phương trình
( )
2
2 –1 –2 0x m xm−=
(m là tham số). Tìm số dương m để
phương trình có hai nghiệm phân biệt x1, x2 sao cho
2
1 12
– 5–2 .x xx m+=
Câu 4 (3,0 điểm).
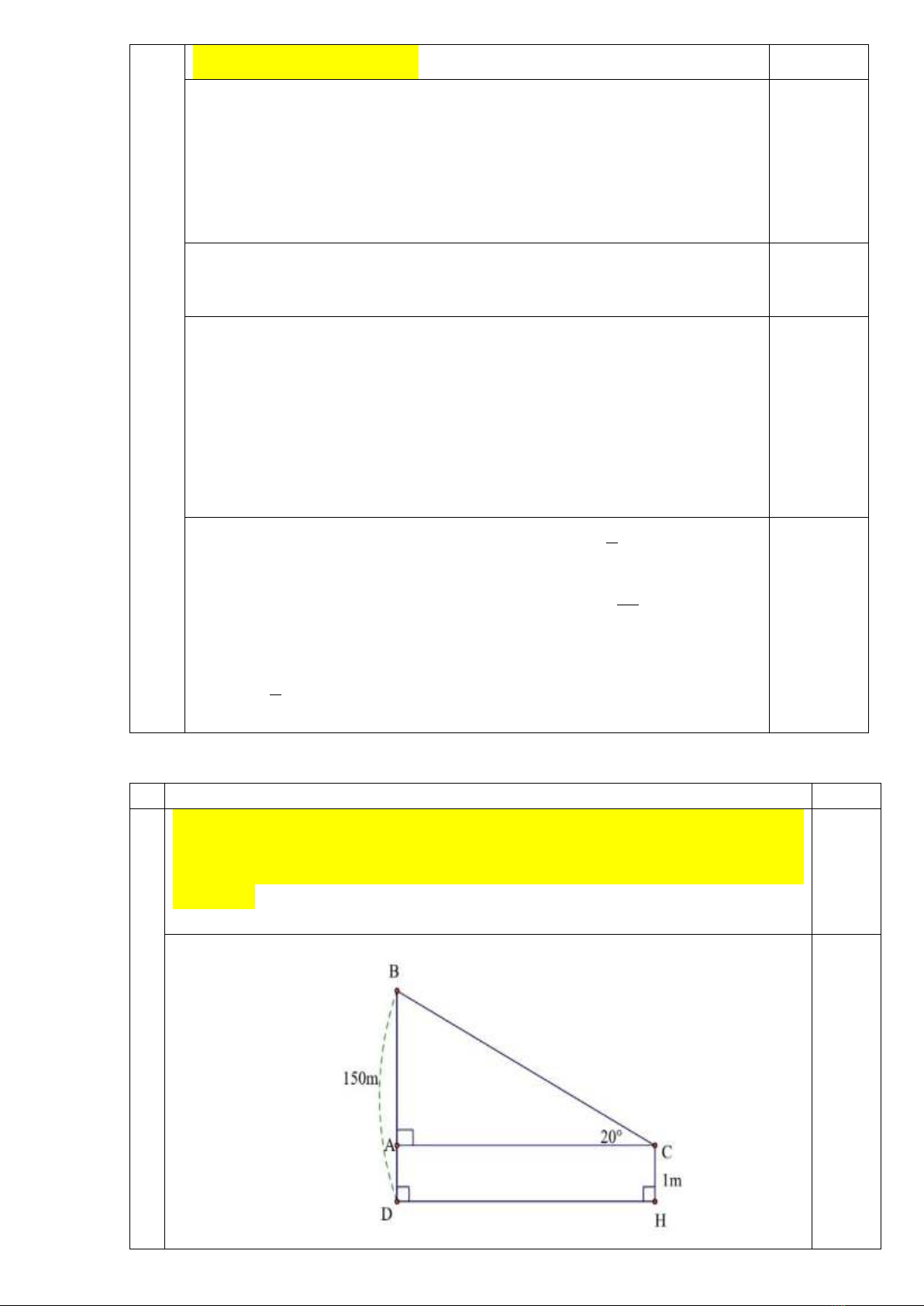
1) Một học sinh đứng ở mặt đất cách tháp ăng ten (có độ cao 150 m) nhìn thấy đỉnh
tháp theo một góc nghiêng lên là
20°
và khoảng cách từ mắt đến mặt đất là 1m. Tính
khoảng cách từ học sinh đó đến tháp (làm tròn đến mét).
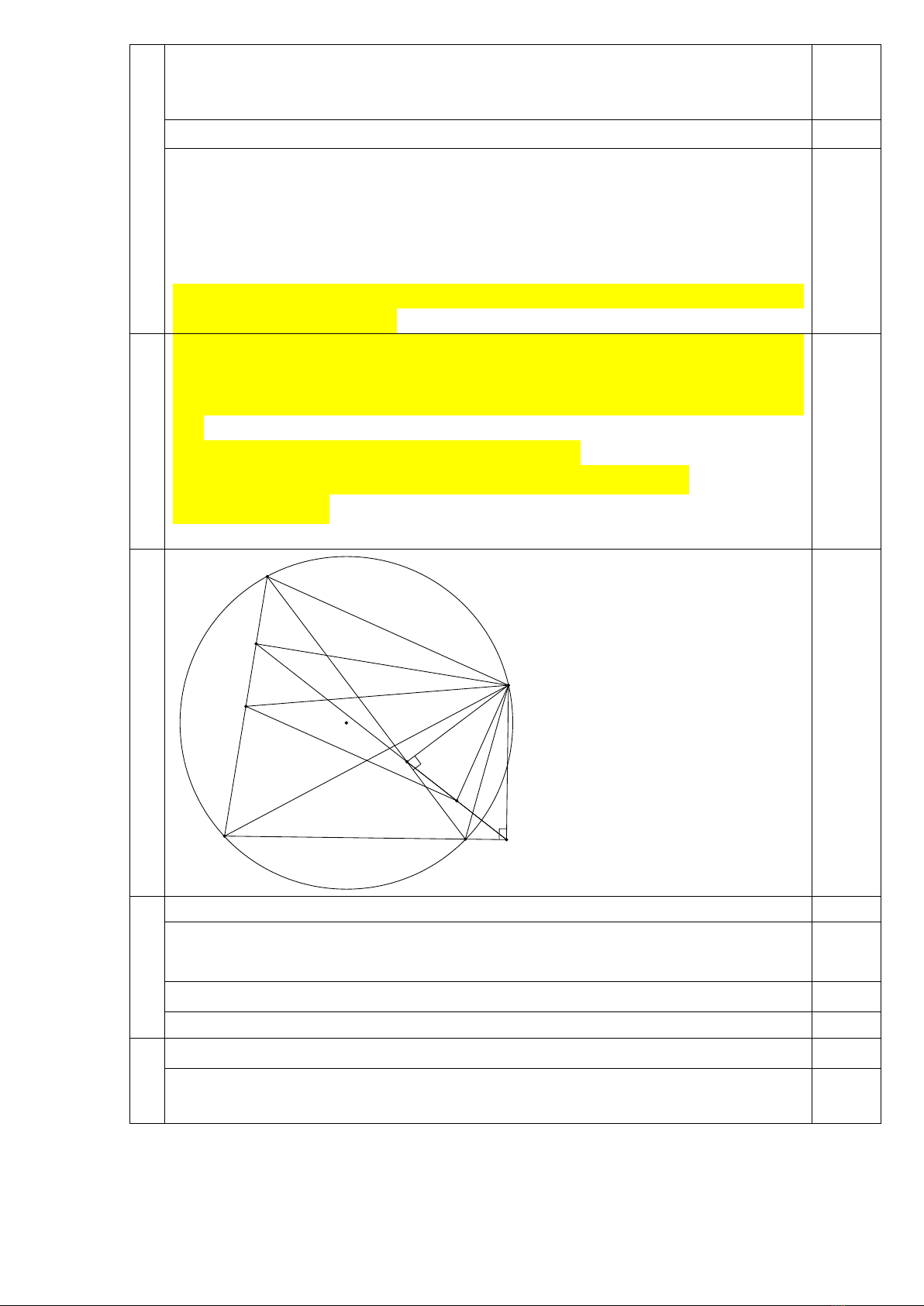
2) Cho ∆ABC có ba góc nhọn nội tiếp đường tròn tâm O. M là một điểm trên cung
nhỏ AC, sao cho
AM CM>
. Từ M hạ ME vuông góc với AC, MF vuông góc với BC. P là
trung điểm của AB, Q là trung điểm của FE.
a) Chứng minh tứ giác MECF nội tiếp.
b) Tia FE cắt AB tại N. Chứng minh:
0
90MNP =
và
22 2
PM PQ QM= +
Câu 5 (1,0 điểm).
Cho các số dương x, y, z thoả mãn x + y + z = 3.
Tìm giá trị nhỏ nhất của Q =
3
9
2
4
1
1
+
+
+
+
+zyx
---------------- Hết -------------