Trang 1/17 - Mã đề thi 144
TRƯỜNG THPT ………….
TỔ TOÁN
BÀI:………………….
NĂM HỌC 2018 – 2019
Môn: Toán - Lớp 11 - Chương trình chuẩn
ĐỀ CHÍNH THỨC Thời gian: ……… phút
Mã đề thi
144
Họ và tên:
………………………………………….
Lớp:
……………...……..………
Câu 1. Tìm
m
để hàm số 2
3
2sin sin 1
x
y
x m x
xác định trên
.
A.
; 2 2 2 2;m
 
. B.
2 2;2 2
m .
C.
2 2;2 2
m
. D.
2 2;2 2
m .
Lời giải
Chọn D
Hàm số xác định trên
khi và chỉ khi 2
2sin sin 1 0,x m x x
.
Đặt
sint x
1;1
t
Lúc này ta đi tìm điều kiện của
m
để
2
2 1 0, 1;1
f t t mt t
Ta có 2
8
tm
TH 1: 2
0 8 0
tm
2 2 2 2
m . Khi đó
0,f t t
(thỏa mãn).
TH 2: 2
0 8 0
tm
2 2
2 2
m
m
(thử lại thì cả hai trường hợp đều không thỏa mãn).
TH 3: 2
0 8 0
tm
2 2
2 2
m
m
khi đó tam thức
2
2 1f t t mt
có hai nghiệm phân
biệt
1 2 1 2
;
t t t t
.
Để
0, 1;1
f t t thì
22
1
22
2
8
1 1 8 4
4
8
1 1 8 4
4
m m
t m m VN
m m
t m m VN
.
Vậy
2 2;2 2
m thỏa mãn yêu cầu bài toán.
Câu 2. Giá trị nhỏ nhất của hàm số
sin 1
cos 2
x
y
x
là:
A.
2
2
. B.
2
2
. C.
0
. D.
1
2
.
Lời giải
Chọn C
Cách 1 : Tương tự như phần lý thuyết đã giới thiệu thì ta thấy
cos 2 0,x x
. Vậy
sin 1
sin 1 cos 2
cos 2
x
y x y x
x
s inx cos 1 2 0
y x y
. Ta có
2 2
2 2 2
1 1 2 1 4 4 1y y y y y
2
4
3 4 0 0
3
y y y
.
Vậy
min 0
y
.
Cách 2 : Ta có sin 1 0
0
cos 2 0
xy
x
min 0 sin 1
y khi x
.
Trang 2/17 - Mã đề thi 144
Câu 3. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
2cos 2 3 sin .cos 1y x x x trên đoạn
7
0, 12
lần
lượt là
A.
7 7
0, 0,
12 12
min 0;max 2y y
. B.
7 7
0, 0,
12 12
min 2;max 3y y
.
C.
7 7
0, 0,
12 12
min 0;max 3y y
. D.
7 7
0, 0,
12 12
min 0;max 4y y
.
Lời giải
Chọn C
Biến đổi
2
2cos 2 3 sin .cos 1y x x x thành
2cos 2 2
3
y x
ta có
2cos 2 2
3
y x
. Đặt
23
u x
Từ đề bài ta xét
7 3
0; ;
12 3 2
x u
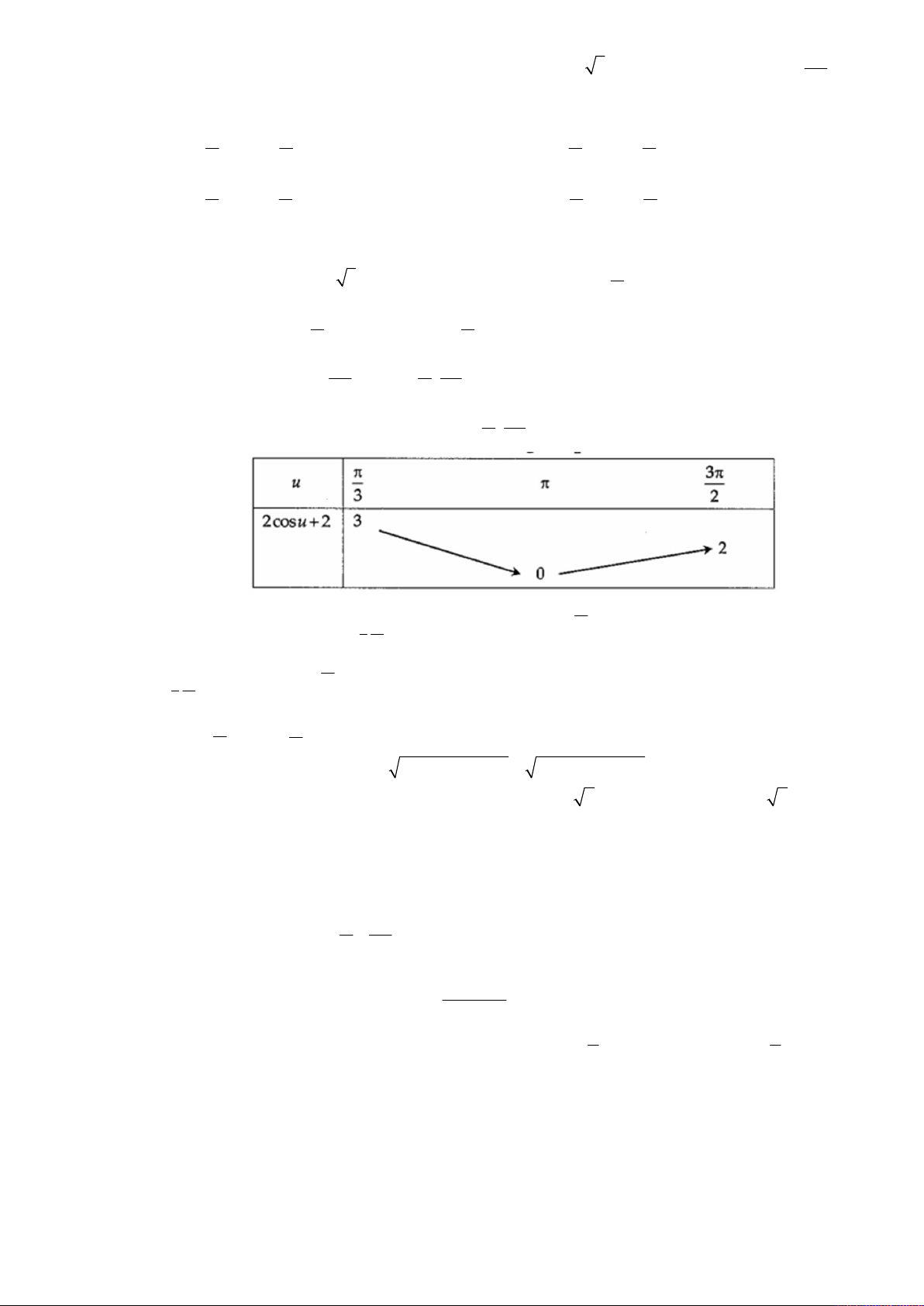
Ta lập BBT của hàm số
2 cos 2y u
trên
3
;
3 2
.
Từ bảng biến thiên ta thấy
3
;
3 2
min (u) 0 khi 3
f u x
3
;
3 2
max (u) 3 khi 0
3
f u x
Hay
77
0; 0;
12 12
min 0; max 3
y y
.
Câu 4. Giá trị lớn nhất của hàm số
2 2 2 2
cos 7sin sin 7cosy x x x x
là
A.
4
. B.
14
. C. 1 7. D. 1 7 .
Lời giải
Chọn A
Ta có
2 2 2 2 2 2 2
1 1 cos 7sin sin 7cosy x x x x
2
16 4y y
Dấu bằng xảy ra khi
,
4 2
k
x k
.
Vậy giá trị lớn nhất của hàm số là 4.
Câu 5. Tìm giá trị lớn nhất
M
của hàm số
2
2
1 tan
yx
.
A.
1
. B.
2
. C.
1
2
M
. D.
2
3
M
.
Lời giải.
Chọn B
Trang 3/17 - Mã đề thi 144
Ta có: 2
2
2
2 2
2cos
1
1 tan
cos
y x
x
x
.
Do 2
0 cos 1 0 2
x y
. Suy ra
2M
.
Câu 6. Tìm tập xác định
D
của hàm số
tan cos
2
y x
.
A. \ 2 ,
2
D k k
. B.
D
.
C.
\ ,D k k
. D. \ ,
2
D k k
.
Lời giải
Chọn C
Hàm số xác định khi và chỉ khi
cos cos 1 2 . *
2 2
x k x k
.
Do k
nên
* cos 1 sin 0 ,x x x k k
.
Vậy tập xác định
\ ,D k k
.
Câu 7. (Chuyên Quang Trung - Bình Phước - Lần 1 - 2018 - BTN) Tập giá trị của hàm số
sin 2 3 cos 2 1y x x
là đoạn
; .a b
Tính tổng
.T a b
A.
2.
T
B.
0.
T
C.
1.
T
D.
1.
T
Lời giải
Chọn A
Cách 1:
sin 2 3 cos 2 1 sin 2 3 cos 2 1y x x x x y
Để phương trình trên có nghiệm thì
22
2 2
1 3 1 2 3 0 1 3
y y y y
.
Suy ra
1;3
y . Vậy
1 3 2.
T
Cách 2: Ta có
1 sin 2 3 cos 2 .y x x
Mặt khác áp dụng bất đẳng thức Bunhiacopskii ta có
2
22 2
1 sin 2 3 os2 1 3 sin 2 os 2 4 2 1 2 1 3.
y x c x x c x y y
Vậy
1 3 2.
T
Cách 3:
sin 2 3 cos 2 1 2sin 2 1
3
y x x x
Do
sin 2 1;1
3
x
nên
2sin 2 1 1;3
3
x
.
Vậy
1 3
y
..sss
Câu 8. Hàm số
sin sin
3
y x x
có bao nhiêu giá trị nguyên?
A.
4
. B.
1
. C.
2
. D.
3
.
Lời giải.
Chọn D
Áp dụng công thức sin sin 2cos sin
2 2
a b a b
a b
ta có
sin sin 2cos cos cos
3 6 6 6
y x x x x
.
Trang 4/17 - Mã đề thi 144
Mà
1 1
cos 1,0
1
,1
6
x y y
.
Câu 9. Cho hàm số
2
cos2
1 sin 3
x
f x
x
và
2
sin 2 cos 3
2 tan
x x
g x
x
. Mệnh đề nào sau đây là đúng?
A.
f x
và
g x
chẵn. B.
f x
chẵn,
g x
lẻ.
C.
f x
và
g x
lẻ. D.
f x
lẻ và
g x
chẵn.
Lời giải
Chọn A
Xét hàm số
2
cos 2
1 sin 3
x
f x
x
.
TXĐ:
D
. Do đó
x D x D
.
Ta có:
2 2
cos 2 cos 2
1 sin 3 1 sin 3
xx
f x f x f x
x x
là hàm số chẵn.
Xét
2
sin 2 cos3
2 tan
x x
g x
x
.
TXĐ: \ ,
2
D k k
. Do đó
x D x D
.
Ta có
2 2
sin 2 cos 3 sin 2 cos3
2 tan 2 tan
x x x x
g x g x g x
x x
là hàm số chẵn.
Câu 10. Hàm số nào có đồ thị nhận trục tung làm trục đối xứng?
A.
1
sin
y
x
. B.
cosy x
. C.
sin 2y x
. D.
sin 2017y x
.
Lời giải
Chọn B
Hàm số chẵn có đồ thị nhận trục tung làm trục đối xứng do đó ta đi tìm hàm số chẵn trong bốn hàm
số đã cho.
Hàm số ở D loại vì lí do tương tự câu 26.
Hàm số A và B là hàm số lẻ. Do vậy ta chọn
C.
Câu 11. Tìm tập giá trị
T
của hàm số
12sin 5cosx
y x
.
A.
7;7
T . B.
13;13
T . C.
17;17
. D.
1;1
T .
Lời giải.
Chọn B
Ta có: 12 5
12sin 5cosx 13 sinx cos
13 13
y x x
.
Đặt 12
cos
13
5
sin
13
.
Khi đó:
13 sin cos sin cos 13siny x a a x x
.
Do đó:
13 13
y
.
Câu 12. Tìm giá trị nhỏ nhất của biểu thức 4 4 2 2
cot cot 2 tan .tan 2
P a b a b
A.
min 2
y
. B.
min 6
y
.
C.
min 4
y
. D. Không tồn tại GTLN.
Trang 5/17 - Mã đề thi 144
Lời giải
Chọn B
2
2 2 2 2 2 2
2
2 2 2 2 2 2
2
2 2 2 2 2 2
22
2 2
cot cot 2cot .cot 2 tan .tan 2
cot cot 2 cot .cot tan .tan 2 6
cot cot 2 cot .cot tan .tan 2cot .cotb.tan .tan 6
cot cot 2 cot .cot tan .tan 6 6
P a b a b a b
a b a b a b
a b a b a b a a b
a b a b a b
Dấu bằng xảy ra khi
2
2 2
2
cot 1
cot cot
cot .cot tan .tan
cot 1
a
a b
a b a b b
,( )
4 2
k
a b k
.
Câu 13. Cho hàm số 4 4
cos siny x x
. Mệnh đề nào sau đây là đúng?
A. 2
,
2
y x
. B. 2,y x
.
C. 1,y x
. D. 2,y x
.
Lời giải.
Chọn C
Ta có
2
4 4 2 2 2 2 2
1
sin cos sin cos 2sin cos 1 sin 2
2
y x x x x x x x
1 1 cos 4 3 1
x
.
Mà 1 3 1 1
1 cos 4 1 cos 4 1 1
2 4 4 2
x x y
.
Câu 14. (Chuyên Phan Bội Châu - Nghệ An - Lần 1 - 2017 - 2018 - BTN) Có bao nhiêu giá trị nguyên
của tham số
m
để hàm số
5 sin 1 cosy m x m x
xác định trên
?
A.
7
. B.
5
. C.
6
. D.
8
.
Lời giải
Chọn D
Hàm số xác định trên
5 sin 1 cos 0m x m x x
sin 1 cos 5m x m x x
Max sin 1 cos 5
xm x m x
.
2
2 2
1 25 12 0 4;3
m m m m m .
Vậy có
8
giá trị nguyên của
m
thỏa mãn.
Câu 15. Giá trị nhỏ nhất của hàm số
2 2
1
3 sin cos
5
f x x x
là
A.
3
. B.
29
10
. C.
59
20
. D.
14
5
.
Lời giải
Chọn C
Ta có
2
2 2 2
1 1 1 1 59
3 sin cos 3 sin cos 3 sin 3
5 20 20 20 20
f x x x x x x .
Vậy GTNN của hàm số là
59
20
.
Câu 16. Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số
được liệt kê ở bốn phương án A, B, C,