Trang 1/12 - Mã đề thi 145
TRƯỜNG THPT ………….
TỔ TOÁN
BÀI:………………….
NĂM HỌC 2018 – 2019
Môn: Toán - Lớp 11 - Chương trình chuẩn
ĐỀ CHÍNH THỨC Thời gian: ……… phút
Mã đề thi
145
Họ và tên:
………………………………………….
Lớp:
……………...……..………
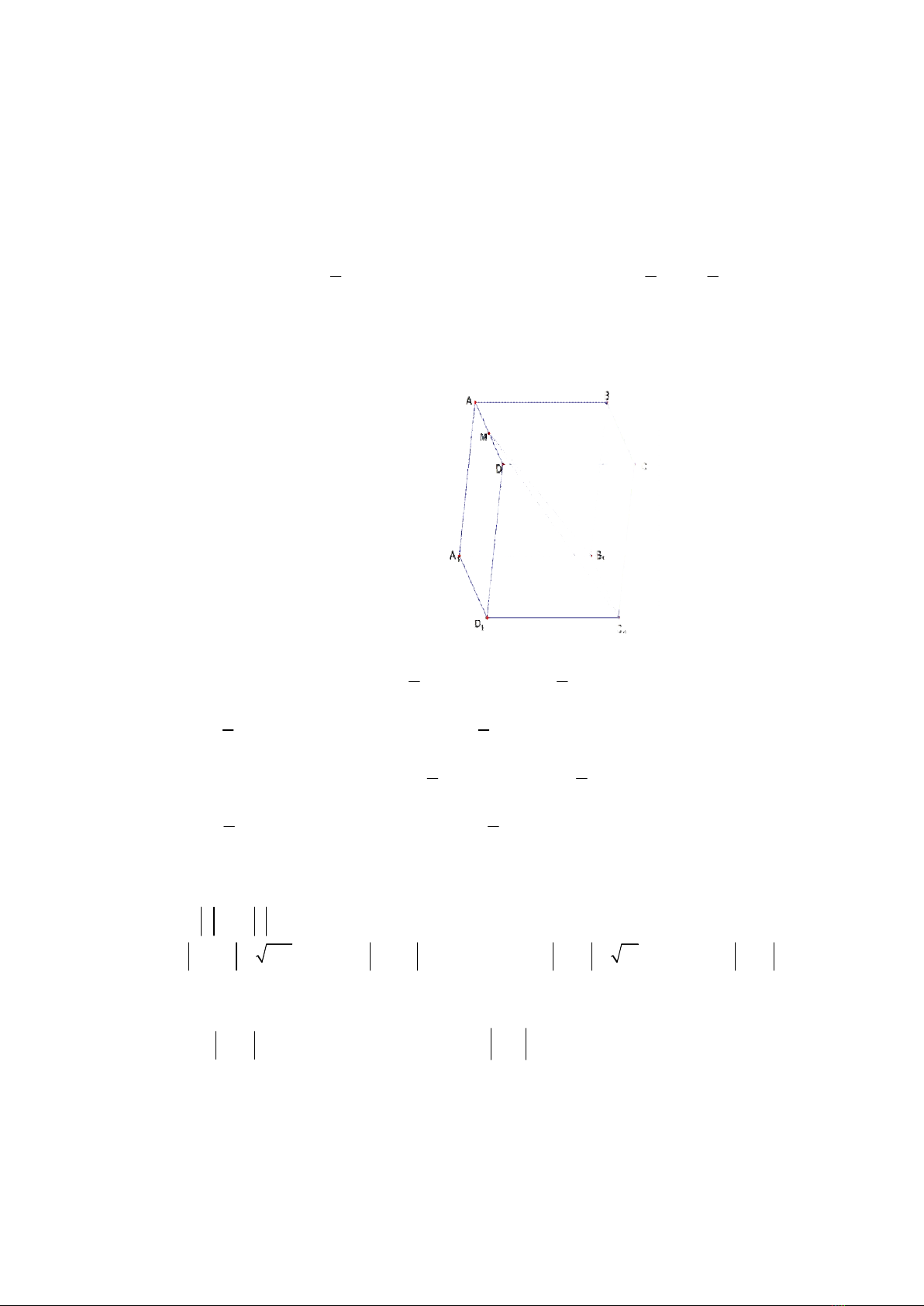
Câu 1. Cho hình hộp .
ABCD A B C D
có tâm
O
. Gọi
I
là tâm hình bình hành
ABCD
. Đặt
AC u
,
CA v
,
BD x
,
. Trong các đẳng thức sau, đẳng thức nào đúng?
A. 1
2 ( )
4
OI u v x y
. B. 1
2 ( )
4
OI u v x y
.
C. 1
2 ( )
2
OI u v x y
. D. 1
2 ( )
2
OI u v x y
.
Lời giải
Chọn B
+ Gọi
J
,
K
lần lượt là trung điểm của
AB
,
CD
.
+ Ta có:
1 1
2 ( )
2 4
OI OJ OK OA OB OC OD u v x y
.
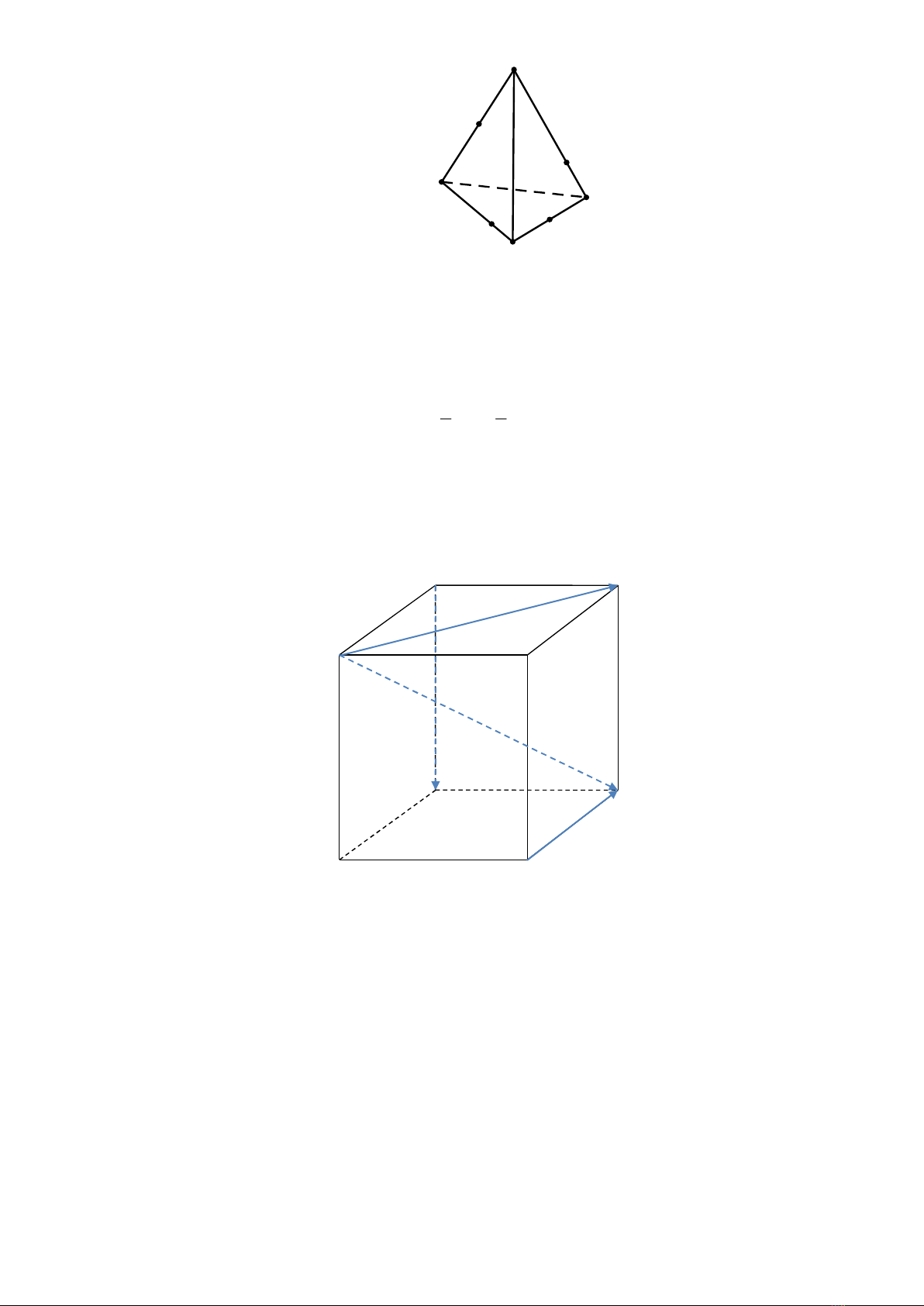
Câu 2. Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và CD. Trên các cạnh AD và BC lần
lượt lấy các điểm P, Q sao cho 3 2
AP AD
, 3 2
BQ BC
. Các vectơ , ,
MP MQ MN
đồng phẳng khi
chúng thỏa mãn đẳng thức vectơ nào sau đây:
A. 3 3
4 4
MN MP MQ
. B. 1 1
2 2
MQ MN MQ
.
C. 2 2
3 3
MN MP MQ
. D. 3 3
2 2
MN MP MQ
.
Lời giải
Chọn A
J
K
O
D
A’ B’
C’
D’
C
B
Trang 2/12 - Mã đề thi 145
Ta có
3 2 3 3 2 2
2 3 1
AP AD AM MP AM MD
AM MD MP

3 2 3 3 2 2
2 3 2
BQ BC BM MQ BM MC
BM MC MQ
Cộng
1
và
2
theo vế suy ra 3 3
4 4
MN MP MQ
.
Câu 3. Cho hình hộp
1 1 1 1
.
ABCD A B C D
. Tìm giá trị của
k
thích hợp điền vào đẳng thức vectơ:
1 1 1 1
AB B C DD k AC
A.
4
k
. B.
1
k
. C.
0
k
. D.
2
k
.
Lời giải
Chọn B
+ Ta có:
1 1 1 1 1
AB B C DD AB BC CC AC
. Nên
1
k
.
Câu 4. Trong không gian cho tam giác
ABC
. Tìm
M
sao cho giá trị của biểu thức
2 2 2
P MA MB MC
 đạt giá trị nhỏ nhất.
A.
M
là tâm đường tròn nội tiếp tam giác
ABC
.
B.
M
là tâm đường tròn ngoại tiếp tam giác
ABC
.
C.
M
là trực tâm tam giác
ABC
.
D.
M
là trọng tâm tam giác
ABC
.
Lời giải
Chọn D
Gọi
G
là trọng tâm tam giác
ABC G
cố định và
0.
GA GB GC
  
A
B
C
D
P
Q
M
N
D
A1 B1
C1
D1
C
B
Trang 3/12 - Mã đề thi 145
2 2 2
2 2 2 2
2 2 2 2 2 2 2
3 2 .
3 .
P MG GA MG GB MG GC
MG MG GA GB GC GA GB GC
MG GA GB GC GA GB GC
     
   
Dấu bằng xảy ra
.M G
Vậy
2 2 2
min
P GA GB GC
với
M G
là trọng tâm tam giác
.ABC
Chọn đáp án A.
Câu 5. Cho hình hộp
1 1 1 1
.
ABCD A B C D
. Gọi
M
là trung điểm
AD
. Chọn đẳng thức đúng.
A.
1 1 1 1 1 1
1
2
C M C C C D C B
. B.
1 1 1 1 1 1
1 1
2 2
C M C C C D C B

.
C. 1 1 1 1 1 1
2
BB B A B C B D
. D.
1 1 1 1 1 1
B M B B B A B C
.
Lời giải
Chọn A
A Sai vì
1 1 1 1 1 1 1 1
1 1
2 2
B M B B BM BB BA BD BB B A B D
 
1 1 1 1 1 1 1 1 1 1 1 1
1 1
2 2
BB B A B A B C BB B A B C
 
.
B Đúng vì
1 1 1 1 1 1 1 1
1 1
2 2
C M C C CM C C CA CD C C C A C D
  
1 1 1 1 1 1 1 1 1 1 1 1
1 1
2 2
C C C B C D C D C C C D C B
.
C Sai. theo câu B suy ra.
D Sai vì
1 1 1 1 1 1 1
BB B A B C BA BC BD
.
Câu 6. Cho
3, 5
a b góc giữa và bằng
120
. Chọn khẳng định sai trong các khẳng định sau?
A.
2 139
a b
. B.
2 9
a b
. C.
19
a b
. D.
7
a b
.
Lời giải
Chọn C
Ta có:
22 2
2 . .cos , 19
a b a b a b a b
Câu 7. Cho hình hộp
1 1 1 1
.
ABCD A B C D
. Chọn khẳng định đúng?
A.
BD
,
1
BD
,
1
BC
đồng phẳng. B.
1
CD
,
AD
,
1 1
A B
đồng phẳng.
C.
1
CD
,
AD
,
1
AC
đồng phẳng. D.
AB
,
AD
,
1
C A
đồng phẳng.
Lời giải
a
b
a b a b a.b.cos a,b
22 2
2 19
Trang 4/12 - Mã đề thi 145
Chọn C
M
,
N
,
P
,
Q
lần lượt là trung điểm của
AB
,
1
AA
,
1
DD
,
CD
.
Ta có
1//
CD MNPQ
,
//
AD MNPQ
,
1//
AC MNPQ
1
CD
,
AD
,
1
AC
đồng phẳng.
Câu 8. Cho tứ diện
ABCD
có các cạnh đều bằng
a
. Hãy chỉ ra mệnh đề sai trong các mệnh đề sau đây:
A.
AB CD
hay
. 0
AB CD
. B.
0
AD CB BC DA
.
C.
2
.
2
a
AB BC
. D.
. .AC AD AC CD

.
Lời giải
Chọn D
Vì
ABCD
là tứ diện đều nên các tam giác
ABC
,
BCD
,
CDA
là các tam giác đều.
A Đúng vì
0
AD CB BC DA DA AD BC CB
.
B Đúng vì
2
. . . .cos60
2
a
AB BC BA BC a a
.
C Sai vì
2
. . .cos 60
2
a
AC AD a a
,
2
. . . .cos60
2
a
AC CD CACD a a
.
D Đúng vì
. 0
AB CD AB CD
.
Câu 9. Cho hình hộp .
ABCD A B C D
. Gọi
I
và
K
lần lượt là tâm của hình bình hành
ABB A
và
BCC B
. Khẳng định nào sau đây sai?
A. 2 2
BD IK BC
. B. Bốn điểm
I
,
K
,
C
,
A
đồng phẳng.
C. 1 1
2 2
IK AC A C

. D. Ba vectơ ; ;
BD IK B C

không đồng phẳng.
Lời giải
Chọn D
D
A1 B1
C1
D1
C
B
Trang 5/12 - Mã đề thi 145
A Đúng vì
IK
,
AC
cùng thuộc
B AC
.
B Đúng vì
1 1 1 1 1
2 2 2 2 2
IK IB B K a b a c b c AC A C
.
C Sai vì
1 1 1
2 2 2
IK IB B K a b a c b c
.
2 2 2
BD IK b c b c c B C
ba véctơ đồng phẳng.
D Đúng vì theo câu C 2 2 2 2
BD IK b c b c c B C BC
.
Câu 10. Trong không gian cho tam giác
ABC
có trọng tâm
G
. Chọn hệ thức đúng?
A.
2 2 2 2 2 2
4
AB AC BC GA GB GC
. B.
2 2 2 2 2 2
3
AB AC BC GA GB GC
.
C.
2 2 2 2 2 2
2
AB AC BC GA GB GC
. D.
2 2 2 2 2 2
AB AC BC GA GB GC
.
Lời giải
Chọn B
Cách 1
Ta có
2
2 2 2
2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2
0
2 . 2 . 2 . 0
0
3
GA GB GC
GA GB GC GAGB GAGC GB GC
GA GB GC GA GB AB GA GC AC GB GC BC
AB AC BC GA GB GC
Cách 2: Ta có:
2 2 2
22 2 2
24
2 4
.
9 2 4
2
3
AB AC BC
MA
AB AC BC
GA
GA MA
Tương tự ta suy ra được
2 2 2 2 2 2 2 2 2
2 2 2
2 2 2
2 2 2 2 2 2
4
.
9 2 4 2 4 2 4
1.
3
3
AB AC BC BA BC AC CA CB AB
GA GB GC
AB BC CA
GA GB GC AB BC CA

Cách 3: Chuẩn hóa giả sử tam giác
ABC
đều có cạnh là
1.
Khi đó
2 2 2
2 2 2 2 2 2
2 2 2
3
3 .
1
AB BC CA
GA GB GC AB BC CA
GA GB GC
Câu 11. Cho hình lập phương .
ABCD A B C D
có cạnh bằng
a
. Hãy tìm mệnh đề sai trong những mệnh đề
sau đây:
A.
3AC a
. B.
2
.
AD AB a
.
C.
. 0
AB CD
. D.
2 0
AB B C CD D A
.
Lời giải
Chọn D