1
PHÒNG GD & ĐT THANH OAI Đề THI OLYMPIC TOÁN 7
Trường THCS Thanh Văn Năm học 2013-2014
(Thời gian 120 phút )
Câu 1. (5điểm )
1. Cho c2=ab Chứng minh rằng:
a ;
b
a
c
b
ca
22
22
b; 22
22
c
a
ab
=
a
ab
2. Ba phân số có tổng bằng
70
213 , các tử của chúng tỉ lệ vối 3;4;5, các
mẫu của chúng tỉ lệ vối 5;1;2 .Tìm ba phân số đó.
Câu 2. (6 điểm )
1. Cho đa thức:
f(x) = x17- 2000x16 + 2000x15 - 2000x14 +….+ 2000x – 1
Tính giá trị của đa thức tại x = 1999.
2. Chứng minh rằng nếu m và n là các số tự nhiên thì số:
A = (5m + n + 1) (3m – n + 4) là số chẵn.
Câu 3.(2 điểm ).
Tìm số tự nhiên x để phân số
3
2
87
x
x có giá trị lớn nhất.
Câu 4. (7 điểm ).
1. Cho tam giác ABC cân tại A,
B
= 500.Gọi K là điểm trong tam giác
sao cho KBC
=100, KCB
= 300.
a, Chứng minh BA=BK
b, Tính số đo
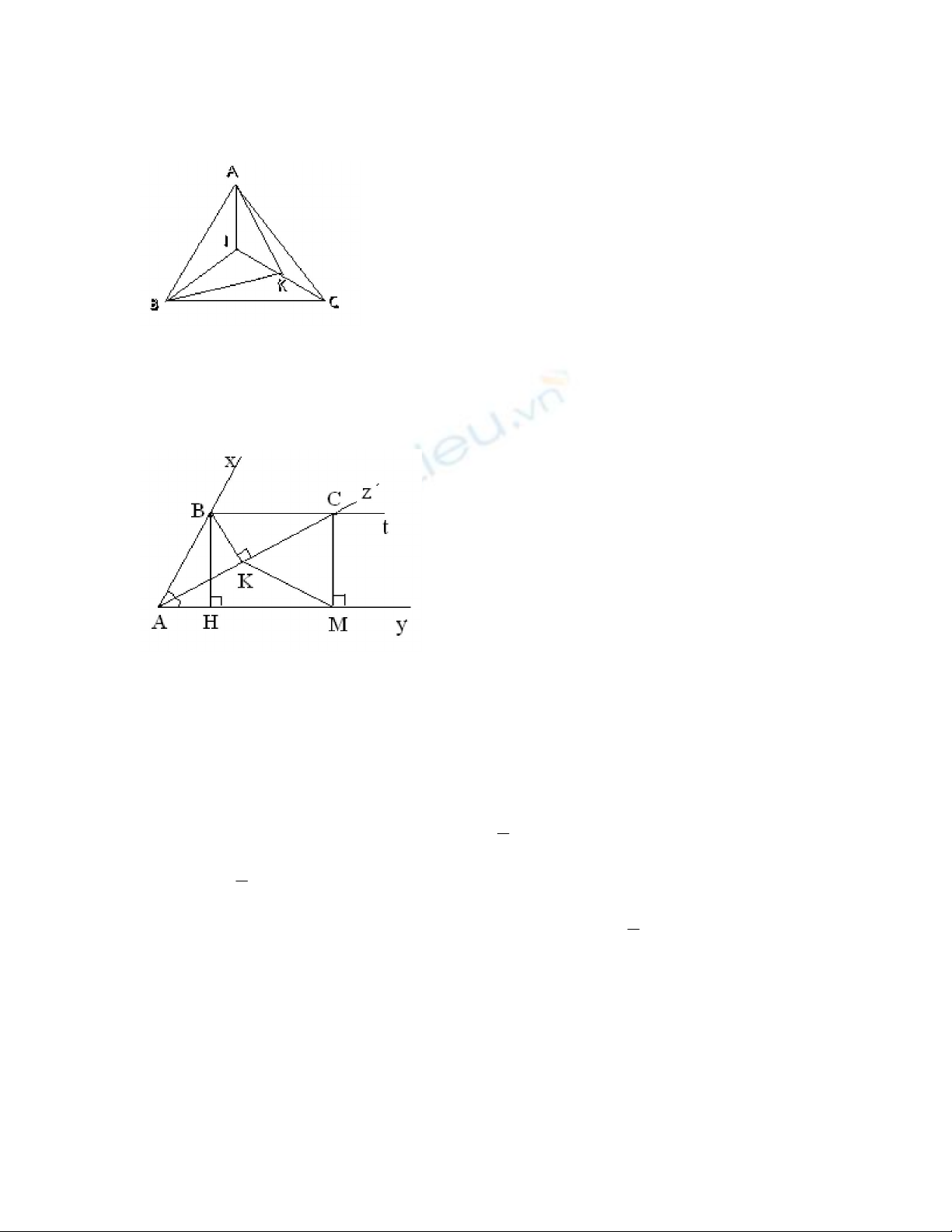
2. Cho
xAy = 600 có tia phân giác Az. Từ điểm B trên Ax kẻ BH
vuông góc với Ay tại H, kẻ BK vuông góc với Az và Bt song song với Ay
,Bt cắt Az tại C. Từ C kẻ CM vuông góc với Ay tại M. Chứng minh :
a, K là trung điểm của AC
b,
KMC là tam giác đều
c, Cho BK = 2 cm . Tính các cạnh
AKM
- Hết-
Duyệt của BGH Người ra đề
Nguyễn Thị Lan Hương
2
ĐÁP ÁN VÀ THANG ĐIỂM OLYMPIC
Môn: Toán 7( Năm 2013-2014)
Câu 1 . (5đ)
1.(2đ) a, Từ c2=a.b
b
c
c
a
b
a
bab
baa
bba
baa
bc
ca
b
c
c
a
.
.
.
2
2
22
22
2
2
2
2
b, Theo câu a ta có a
b
ca
cb
b
a
bc
ca
22
22
22
22
2
2
a
ab
c
a
ab
a
b
c
a
cb
a
b
c
a
cb
22
22
22
22
22
22
....11
2 .(3 đ) Gọi các phân số phải tìm là : a ; b ; c ta có : a+b+c =
70
213
Và a : b : c =
2
5
:
1
4
:
5
3 = 6 : 40 : 25 ……….
Suy ra a =
35
9 ; b =
7
12 ; c =
14
15
Câu 2.(6điểm )
1. (3đ)
f(x) =x17 – 1999x16 – x16 + 1999x15 + x15 – 1999x14 - x14+…+1999x + x – 1
f(1999) = 199917 - 199917 - 199916 + 199916 + 199915 - 199915-
199914+…+19992+1999 – 1
= 1999 – 1 = 1998.
2.(3đ)
Ta xét hiệu (5m + n +1) – (3m – n + 4) = ….. = 2m + 2n – 3
Với m, n
N thì 2m + 2n - 3 là một số lẻ . Do đó trong hai số
5m + n +1 và 3m – n +4 phải có một số chẵn.
Suy ra tích của chúng là một số chẵn .Vậy A là số chẵn.
Câu 3 . (2 đ)
.Đặt A= )32(2
5
2
7
)32(2
5)32(7
)32(2
)87(2
32
87
xx
x
x
x
x
x
Đặt B= )32(2
5
x Thì A lớn nhất khi và chỉ khi B lớn nhất
……GTLN của A=6 khi và chỉ khi x=2
Câu 4;(7 đ)
1.(4đ)
3
a,-vẽ tia phân giác
ABK
cắt CK ở I …. .Ta có IBC
cân nên IB=IC
….. CIABIA
(ccc)
…nên
BIA
CIA
=120o
Do đó
BIK
BIA
(gcg) BKBA
b, ……..Từ phần a ta tính được o
BAK 70
2.(3đ)
V ẽ h ình , GT _ KL
a,
ABC cân tại B do
( )
CAB ACB MAC
và BK là đường cao
BK là
đường trung tuyến
K là trung điểm của AC
b,
ABH =
BAK ( cạnh huyền + góc nhọn )
BH = AK ( hai cạnh t. ư ) mà AK =
1
2
AC
BH =
1
2
AC
Ta có : BH = CM ( t/c cặp đoạn chắn ) mà CK = BH =
1
2
AC
CM = CK
MKC là tam giác cân ( 1 )
Mặt khác :
MCB
= 900 và
ACB
= 300
MCK
= 600 (2)
Từ (1) và (2)
MKC là tam giác đều
c) Vì
ABK vuông tại K mà góc KAB = 300 => AB = 2BK =2.2 = 4cm
Vì
ABK vuông tại K nên theo Pitago ta có:
4
AK = 2 2
16 4 12
AB BK
Mà KC =
1
2
AC => KC = AK =
12
KCM đều => KC = KM =
12
Theo phần b) AB = BC = 4
AH = BK = 2
HM = BC ( HBCM là hình chữ nhật)
=> AM = AH + HM = 6