M
a
2
a
3
M
2
d
d
A
B
C
Hình 2
Hình 1
2
a
a
A
B
C
0
60
,
E F
q
a
a
a
M
P
2
P
M
x
y
z
A
B
C
D
Hình 3
P
Baøi 1: ( 2 ñieåm)
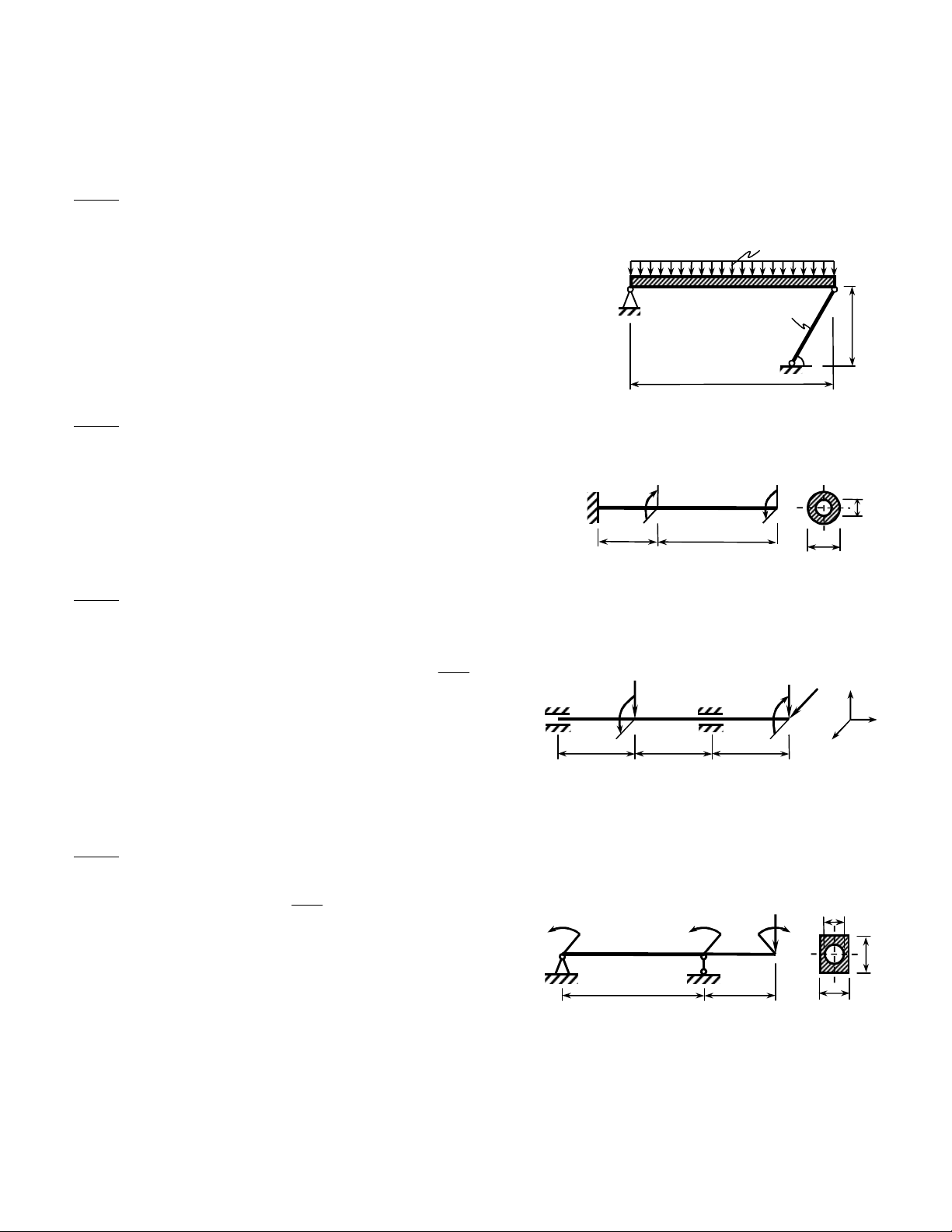
Thanh AB tuyeät ñoái cöùng chòu lieân keát goái coá ñònh taïi A, ñaàu B ñöôïc giöõ bôûi thanh BC nhö hình 1. Thanh
BC laøm baèng vaät lieäu coù moâñun ñaøn hoài
E
, öùng suaát cho pheùp
vaø coù dieän tích maët caét ngang
F
.
Bieát
2
250 / ; 1,5 ; 25 /
q kN m a m kN cm
a) Xaùc ñònh phaûn löïc lieân keát taïi goái A vaø öùng löïc trong BC theo
q
vaø
a
.
b) Xaùc ñònh trò soá
F
ñeå thanh BC beàn.
c) Tính bieán daïng cuûa thanh BC theo
, , ,
q a E F
.
Baøi 2: (2 ñieåm)
Truïc AC coù maët caét ngang hình vaønh khaên, lieân keát, chòu löïc vaø coù kích thöôùc nhö hình 2.
Bieát
2
50 . ; 0,3 ; 12 / ;
M kN m a m kN cm
a) Veõ bieåu ñoà noäi löïc xuaát hieän trong truïc theo
M
.
b) Xaùc ñònh kích thöôùc maët caét ngang
d
ñeå truïc beàn.
c) Tính goùc xoay cuûa maët caét ngang taïi C so vôùi maët caét ngang
taïi A.
Baøi 3: (3,5 ñieåm)
Truïc AD ñoàng chaát, coù maët caét ngang hình troøn ñöôøng kính d, ñöôïc ñôû treân hai oå laên taïi A vaø C (Boû qua
ma saùt taïi caùc oå laên naøy). Caùc taûi troïng taùc duïng leân truïc vaø kích thöôùc nhö hình 3.
Bieát:
.
M P a
; 30
P KN
;
30
a cm
;
2
cm
KN
12
.
a) Xaùc ñònh phaûn löïc taïi caùc oå laên A , C theo
P
.
b) Veõ caùc bieåu ñoà noäi löïc xuaát hieän trong truïc theo
,
P a
.
c) Boû qua aûnh höôûng cuûa löïc caét, xaùc ñònh ñöôøng kính
d cuûa truïc theo thuyeát beàn thöù ba (thuyeát beàn öùng
suaát tieáp).
Baøi 4: (2,5 ñieåm)
Daàm AC ñoàng chaát, maët caét ngang khoâng ñoåi, lieân keát, chòu löïc vaø coù kích thöôùc nhö hình 4.
Bieát: 150
P KN
;
2
cm
KN
12
;
1,2
a m
.
a) Xaùc ñònh phaûn löïc taïi A , B theo
P
.
b) Veõ caùc bieåu ñoà noäi löïc xuaát hieän trong truïc theo
,
P a
.
c) Boû qua aûnh höôûng cuûa löïc caét, xaùc ñònh kích thöôùc
maët caét ngang
b
theo ñieàu kieän beàn
--------------- Heát ---------------
Ghi chuù:
- Caùn boä coi thi khoâng giaûi thích ñeà thi.
ÑAÏI HOÏC SÖ PHAÏM KYÕ THUAÄT
TP.HCM
Khoa Xaây Döïng & Cô Hoïc ÖÙng Duïng
Boä moân Cô Hoïc
Ñeà thi moân:
Söùc Beàn Vaät Lieäu
Maõ moân hoïc: 1121100
Ñeà soá: 01. Ñeà thi coù 01 trang
Thôøi gian: 90 Phuùt
Khoâng söû duïng taøi lieäu
Ngaøy 25 thaùng 05 naêm 2010
Chuû nhieäm Boä Moân
a
M Pa
3
M
2
a
P
M
A
B
C
2
b
3
b
b
Hình
4
Hình 1
2
a
A
B
0
60
q
A
Y
A
X
B
N
ÑAÙP AÙN SBVL. Maõ moân hoïc: 1121100. Ñeà soá: 1. Ngaøy thi: 26/ 06 / 2010.
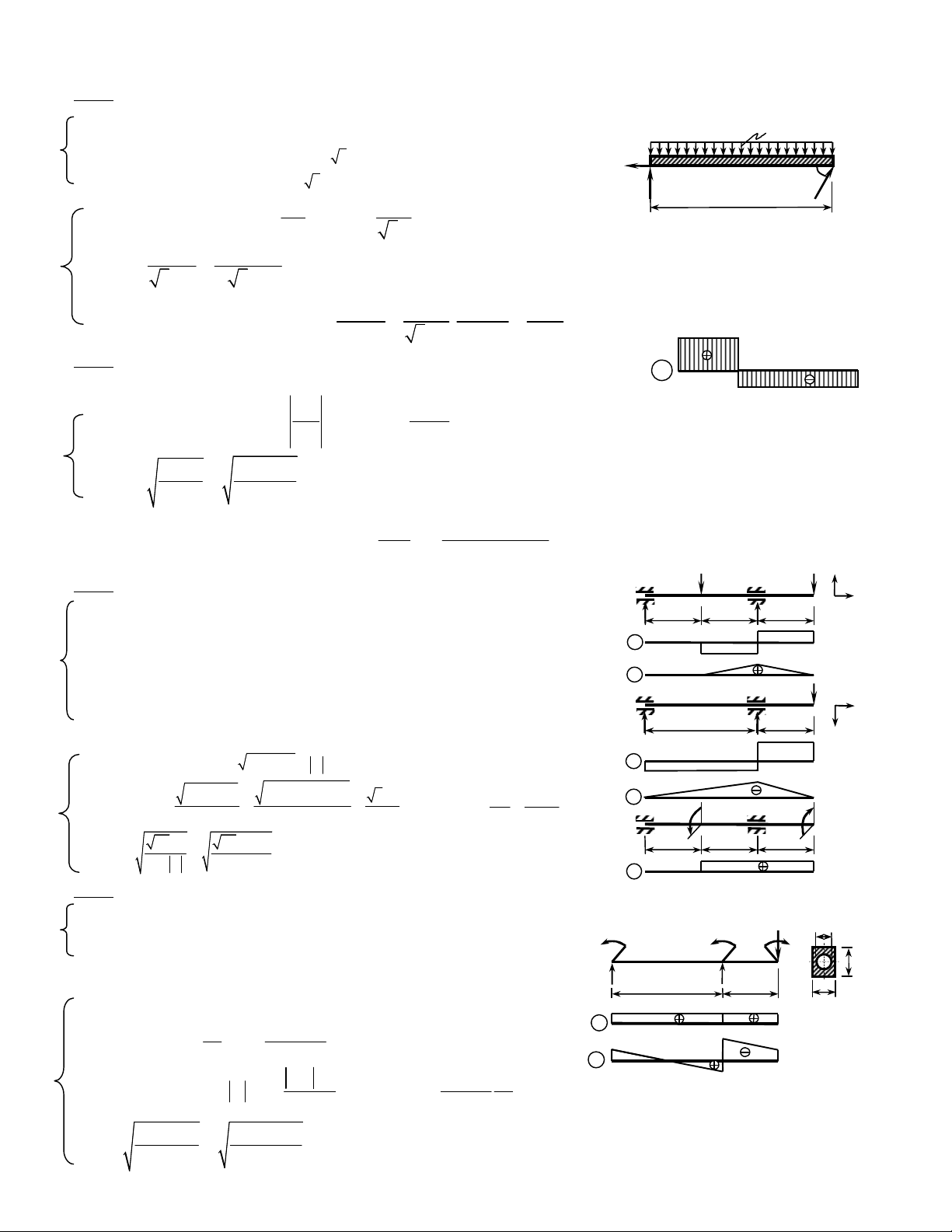
Baøi 1: <2 Ñieåm>
a) Xaùc ñònh phaûn löïc: xeùt caân baèng thanh AC nhö hình 1. -----------(0,25ñ)
2 .2 . 0
B A
m Y a q a a
A
Y qa
------------------------------ (0,25ñ)
0
2 sin 60 0
y A B
F Y qa N
2 / 3
B
N qa ------------------ (0,25ñ)
0
cos60 0
x A B
F X N
/ 3
A
X qa ---------------------- (0,25ñ)
b) Theo điều kiện bền:
2
3
B
z
N qa
FF
......... (0,25ñ)
2
2 2.250.1,5 17,32
3 3.25
qa
F cm
---------- (0,25ñ) Chọn
2
17,4
F cm
-------------- (0,25ñ)
c) Biến dạng của thanh BC:
2
0
2 4
.
EF cos30 3
3
B BC
BC
N L
qa a qa
L
EF
EF
----------------------- (0,25ñ)
Baøi 2: <2 Ñieåm>
a) Biểu đồ nội lực nhö hình 2. -----------(0,75ñ)
b) Theo điều kiện bền:
ax 3
max
2
W 1,5
z
m
M M
d
........ (0,25ñ)
2
3
32 2.50.10
8, 22
1,5 1,5.12
M
d cm
------------- (0,25ñ) Chọn
8,3
d cm
-------------- (0,25ñ)
c) Goùc xoay của mặt cắt tại A:
2
4
1
.2 2 .
0
.1,5
z
M
AC
ii
SM a M a
GJ G d
--------------------- (0,5ñ)
Baøi 3: <3,5 Ñieåm>
a) Trong maët phaúng (yz):
. .2 .3 0
A C
m P a Y a P a
2
C
Y P
------------------------- (0,25ñ)
.2 . . 0
C A
m Y a P a P a
0
A
Y
---------------------------- (0,25ñ)
Trong maët phaúng (xz):
.2 2 .3 0
A C
m X a P a
3
C
X P
--------------------------- (0,25ñ)
.2 2 . 0
C A
m X a P a
A
X P
----------------------------- (0,25ñ)
b) Bieåu ñoà noäi löïc nhö hình 3 ---------------------------- (1,5ñ)
c) Theo thuyeát beàn 3: 2 2
4
(*)
Trong ñoù:
2 2
2 2
3 3
2
5
0,1 0,1
x y
x
M M Pa Pa
Pa
W d d
----(0,25ñ)
3
0,2
z
M Pa
W d
-- (0,25ñ)
(*) 3
324 24.30.30
12,24
0,2 0,2.12
Pa
d cm
-------(0,25ñ) Choïn
12,3
d cm
---- (0,25ñ)
Baøi 4: <2,5 Ñieåm>
a) Xaùc ñònh phaûn löïc: xeùt caân baèng daàm AC nhö hình 4.
.2 3 .3 0
A C
m Pa Y a Pa P a Pa
0
C
Y
---------------- (0,25ñ)
.2 3 . 0
C A
m Y a Pa Pa P a Pa
A
Y P
------------------ (0,25ñ)
b) Bieåu ñoà noäi löïc nhö hình 4 -------------------------------- (1 ñ)
c) Choïn maët caét khaûo saùt taïi B:
3
4 4
max
2 . 3
3
2 ; ; 0,05 4,45
2 12
x x
b b
b
M Pa y J b b
------------ (0,25ñ)
Theo ñieàu kieän beàn:
max max 4
ax
2 3
.
J 4,45 2
x
m
x
MPa b
yb
------- (0,25ñ)
3
33 3.150.120 10,03
4,45. 4,45.12
Pa
b cm
----------- (0,25ñ) Choïn
10,1
b cm
---------- (0,25ñ)
1ñ
1ñ
M
2
M
z
M
Hình
2
0,75ñ
a
a
a
P
P
x
y
z
A
B
C
D
x
Q
x
M
y
M
z
M
2
a
a
2
P
z
A
C
D
y
Q
A
Y
C
Y
P
P
Pa
a
a
a
M
M
A
B
C
D
A
X
C
X
2
P
P
2
Pa
Pa
Hình 3
1ñ
1ñ
a
M Pa
3
M
2
a
P
M
A
B
C
2
b
3
b
b
P
Pa
Pa
Pa
2
Pa
y
Q
x
M
Hình
4
A
Y
C
Y
0,5ñ
1ñ
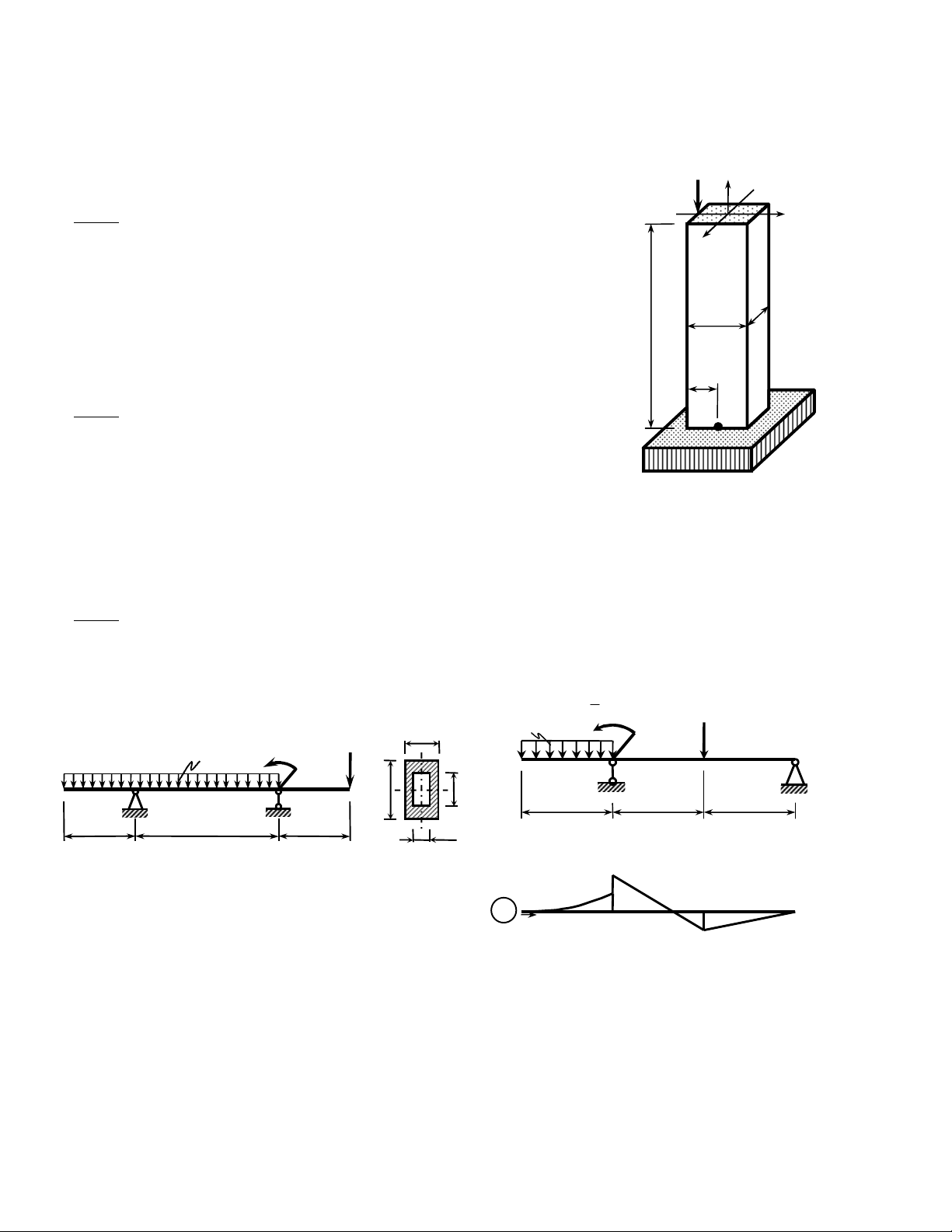
Baøi 1: (4 ñieåm)
Coät AB coù maët caét ngang hình chöõ nhaät kích thöôùc 2
b b
lieân keát vaø chòu löïc
nhö hình 1. Boû qua troïng löôïng baûn thaân coät.
a) Veõ bieåu ñoà noäi löïc xuaát hieän trong coät theo
,
P b
.
b) Vieát phöông trình ñöôøng trung hoøa cuûa maët caét taïi A theo
b
.
c) Xaùc ñònh öùng suaát keùo vaø öùng suaát neùn lôùn nhaát trong coät theo
,
P b
.
d) Xaùc ñònh öùng suaát phaùp taïi ñieåm O theo
,
P b
.
Baøi 2: ( 4 ñieåm)
Daàm AD coù maët caét ngang , lieân keát, chòu löïc vaø kích thöôùc nhö hình 2. Daàm
laøm cuøng moät loaïi vaät lieäu öùng suaát cho pheùp
.
Bieát
2
10 / ; 0.8 ; 12 /
q kN m a m kN cm
d) Xaùc ñònh phaûn löïc lieân keát taïi caùc goái B, C theo
q
vaø
a
.
e) Veõ bieåu ñoà löïc caét, moâmen uoán phaùt sinh trong daàm theo
q
vaø
a
.
f) Boû qua aûnh höôûng cuûa löïc caét, xaùc ñònh kích thöôùc maët caét ngang (
b
) cuûa daàm theo ñieàu kieän beàn.
Baøi 3: (2 ñieåm)
Cho daàm AC coù ñoä cöùng choáng uoán
EJ const
, lieân keát vaø chòu löïc nhö hình 3a. Bieåu ñoà moâmen uoán
x
M
phaùt sinh trong daàm nhö hình 3b. Tính chuyeån vò thaúng ñöùng cuûa maët caét taïi A theo
, ,
q a EJ
.
--------------- Heát ---------------
Ghi chuù:
- Caùn boä coi thi khoâng giaûi thích ñeà thi.
ÑAÏI HOÏC SÖ PHAÏM KYÕ THUAÄT TP.HCM
Khoa Xaây Döïng & Cô Hoïc ÖÙng Duïng
Boä moân Cô Hoïc
Ñeà thi moân:
Söùc Beàn Vaät Lieäu.
Maõ moân hoïc: 1121080.
Ñeà soá: 01. Ñeà thi coù 01 trang.
Thôøi gian: 90 Phuùt
Khoâng söû duïng taøi lieäu.
Ngaøy
21
thaùng
05
naêm
200
9
Chuû nhieäm Boä Moân
q
a
a
2a
Hình
2
M=3qa
2
P=qa
A
B
C
D
4b
2b
4b
7b
A
O
B
a
b
2
y
x
P
z
b
Hình
1
P=2
qa
q
a
a
a
A
B
C
D
2
0,5
qa
2
qa
2
0,5
qa
Mx
Hình
3a
Hình
3b
2
1
2
M qa
ÑAÙP AÙN SBVL. Maõ moân hoïc: 1121080. Ñeà soá: 1. Ngaøy thi: 11/ 06 / 2009.
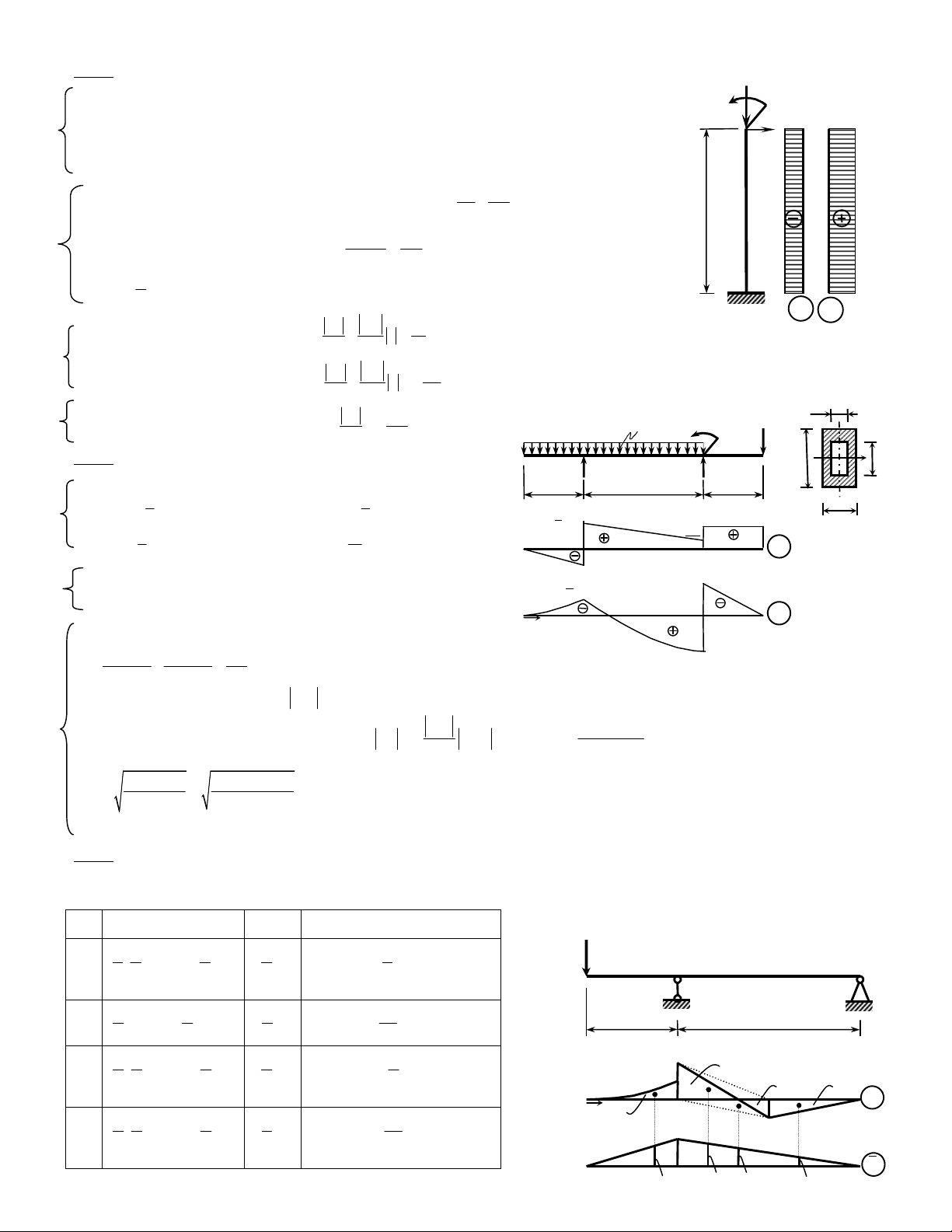
Baøi 1: <4 Ñieåm>
a) Veõ bieåu ñoà noäi löïc
Sô ñoà tính cuûa coät nhö hình 1a --------------------------------------------- (0,5ñ)
Bieåu ñoà löïc doïc
z
N
nhö hình 1b-------------------------------------------- (0.5ñ)
Bieåu ñoà moâmen uoán
y
M
nhö hình 1c -------------------------------------- (0,5ñ)
b) Phöông trình ñöôøng trung hoøa cuûa maët caét taïi A:
0
y
z
y
M
Nx
F J
(0,25ñ)
Trong ñoù:
3
4
22
2
; 2 ; ;
12 3
z y y
b b
b
N P F b M Pb J -------------- (0,5ñ)
3
b
x
----------------------------------------------------------- (0,25ñ)
c) ÖÙng suaát keùo lôùn nhaát: max
2
y
z
y
M
N
P
x
F J b
------------- (0,5ñ)
ÖÙng suaát neùn lôùn nhaát: min
2
2
y
z
y
M
N
P
x
F J b
----------- (0,5ñ)
d) ÖÙng suaát phaùp taïi ñieåm O:
2
2
z
z
N
P
F b
----------------- (0,5ñ)
Baøi 2: <4 Ñieåm>
d) Xaùc ñònh phaûn löïc: xeùt caân baèng thanh AD nhö hình 2a.
2
1
3 3 2 3 0
2
B C
m q a a qa N a qa a
3
4
C
N qa
----------- (0,25ñ)
2
3
3 2 3 . 0
2
C B
m q a a N a qa qa a
13
4
B
N qa
------------- (0,25ñ)
e) Bieåu ñoà löïc caét
y
Q
nhö hình 2b .............................. (0,75ñ)
Bieåu ñoà moâmen uoán
x
M
nhö hình 2c --------------- (0,75ñ)
f) Xaùc ñònh
b
theo ñieàu kieän beàn
3 3
4 4
4 . 7 2 . 4 311
103,67
12 12 3
x
b b b b
J b b
----------------------------------------- (0,5ñ)
Choïn maët caét khaûo saùt taïi C: 2
max
max
2 ; 3,5
x
M qa y b
-------------- (0,25ñ)
Theo ñieàu kieän beàn öùng suaát phaùp:
max
max
C
x
z
x
My
J
2
4
23,5
103,67
qa b
b
----------- (0,5ñ)
2 2
3
34
2.3,5. 2.3,5.10.0,8
0,0153
103,67 103, 67.12.10
qa
b m
----------------- (0,5)
Choïn 1,6
b cm
------------------------------------------ (0,25ñ)
Baøi 3: <2 Ñieåm>
Bieåu ñoà moâmen uoán ôû traïng thaùi “m” (hình 3b); Traïng thaùi “k” (hình 3a); Bieåu ñoà moâmen uoán ôû traïng thaùi
“k” (hình 3c) ------------------------------------------------------------- (0,5ñ)
TT
i
i
c
f
i
i c
f
1
2 3
1 1 1
. .
3 2 6
qa a qa
3
4
a
4
1
8
qa
2
2 3
1 1
.
2 2
qa a qa
5
6
a
4
5
12
qa
3
2 3
1 1 1
. .
2 2 4
qa a qa
2
3
a
4
1
6
qa
4
2 3
1 1 1
. .
2 2 4
qa a qa
1
3
a
4
1
12
qa
0,5ñ
2ñ
A
a
x
M
=Pb
P
B
Nz My
a)
b)
c)
P
P
b
Hình 1
1,5ñ
0,5
ñ
1ñ
1ñ
q
M=3qa
2
P=q
a
a
2a
a
9
4
qa
qa
4
qa
qa
2
1
2
qa
2
2
qa
2
qa
Qy
M
x
a)
b)
c)
NBNC
A
B
C
D
4b
2b
4b
x
Hình
2
d)
7b
1,5
ñ
(0,5ñ)
(0,25ñ)
(
0,
2
5ñ
)
P
k
=
1
a
2a
A
B
D
2
0,5
qa
a
2
qa
2
0,5
qa
2
1
c
f
3
4
2
c
f
3
c
f
4
c
f
1
a)
b)
c)
Hình
3
M
x
x
M
(0,25ñ)

3
1
1
i
A i C
i
f
EJ
4 4
70,2917
24
qa qa
EJ EJ
(0,25ñ)










![Đề thi Cơ học kết cấu 2 học kì 1 năm 2023-2024 có đáp án [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250206/gaupanda072/135x160/9031738814568.jpg)


![Câu hỏi ôn tập Tổ chức thi công [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251015/khanhchi0906/135x160/38451768553582.jpg)












