PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HUYỆN NÔNG CỐNG
ĐỀ THI THỬ VÀO LỚP 10 THPT
NĂM HỌC: 2024-2025
MÔN: TOÁN
Thời gian làm bài:120 phút
(Không kể thời gian giao đề)
Ngày thi: 25/5/2024
(Đề thi có 5 câu và 1 trang)
Câu 1. (2 điểm)
Cho biểu thức:
241
:
1
11 1
aaa
Aa
aa a

−
= −+


−
+− +

( a
≥
0; a
1≠
)
1. Rút gọn biểu thức A
2. Tính giá trị của biểu thức A khi
4 23a= −
Câu 2. (2 điểm)
1. Giải hệ phương trình:
47
35
xy
xy
−=
+=
2. Viết phương trình đường thẳng (d) đi qua hai điểm M(1;5) và N(2;8).
Câu 3. (2 điểm)
1. Giải phương trình
2
7 10 0xx−+=
2. Cho phương trình
với 𝑚𝑚 là tham số. Tìm 𝑚𝑚 để phương
trình có hai nghiệm phân biệt 𝑥𝑥1,𝑥𝑥2 thỏa mãn:
Câu 4. (3 điểm)
Cho đường tròn
( )
O
, bán kính
( )
>0RR
và dây cung BC cố định. Một điểm A chuyển động
trên cung lớn BC sao cho tam giác ABC có ba góc nhọn. Kẻ các đường cao AD, BE của tam
giác ABC cắt nhau tại H và BE cắt đường tròn
( )
O
tại F (F khác B).
1. Chứng minh rằng tứ giác DHEC nội tiếp.
2. Kẻ đường kính AM của đường tròn
( )
O
và OI vuông góc với BC tại I. Chứng minh rằng
I là trung điểm của HM và tính AF biết
=3.BC R
3. Khi BC cố định, xác định vị trí của A trên đường tròn
()O
để DH.DA lớn nhất.
Câu 5. (1 điểm)
Cho
a,b,c
là ba số thực dương thỏa mãn
ab bc ca 3abc++=
. Tìm giá trị lớn nhất của biểu
thức:
2 22
abc
Ma bc b ca c ab
=++
+++
----------------------------------------------Hết-------------------------------------------
Cán bộ goi thi không giải thích gì thêm!
Họ và tên thí sinh:………………………………........ Số báo danh:…………..
HƯỚNG DẪN CHẤM
Câu Đáp án
Thang
điểm
Câu 1:
Cho biểu thức:
241
:
1
11 1
aaa
Aa
aa a

−
= −+


−
+− +

( a
≥
0; a
1≠
)
1. Rút gọn biểu thức A
2. Tính giá trị của biểu thức A khi
4 23a= −
( 2
điểm)
ĐKXĐ :
0, 1aa≥≠
1)
( )( ) ( )
( )( ) ( )( ) ( )
1
( 1) 2 4 .1
11 11 11
aa
aa a
Aa
aa aa aa

+
−−

= −+ +

+− +− +−

( )( ) ( )
24
.1
11
aaaa a
Aa
aa
−−−+ −
= +
+−
( )( ) ( )
4.1
11
Aa
aa
−
= +
+−
4
1
Aa
−
=−
Vậy
4
1
Aa
−
=−
với
0, 1aa≥≠
0,25
0,25
0,25
0,25
2) Với
0, 1aa≥≠
ta có :
4
1
Aa
−
=−
Ta có:
( )
2
4 23 3 1a=−=−
( thoả mãn ĐKXĐ )
31a⇒=−
Khi đó:
( )
( )( )
4 32
44 43 8
311 3 2 32 32
A
−+
−−
= = = = +
−− − −+
Vậy
43 8A= +
khi
4 23a= −
0,25
0,5
0,25
Câu 2
1. Giải hệ phương trình:
47
35
xy
xy
−=
+=
2. Viết phương trình đường thẳng (d) đi qua hai điểm M(1;5) và
N(2;8).
( 2
điểm)
47
35
xy
xy
−=
+=
12x 3 21
35
y
xy
−=
⇔+=
13x 26
4x 7y
=
⇔= −
2
4.2 7
x
y
=
⇔= −
2
1
x
y
=
⇔=
Vậy hệ phương trình có nghiệm duy nhất là:
( ) ( )
; 2;1xy =
0,75
0,25
Vì
( )
12
MN
xx≠≠
nên phương trình đường thẳng cần tìm có dạng
(d) : y ax b= +
0,25
Vì đường thẳng (d) đi qua điểm
( )
M 1; 5
nên:
ab5+=
và (d) đi qua
điểm
( )
N 2;8
nên:
2a b 8.+=
Ta có:
ab5
2a b 8
+=
+=
a3
b2
=
⇔=
Vậy phương trình đường thẳng
(d) : y 3x 2= +
0,25
0,25
0,25
Câu 3
1. Giải phương trình
2
7 10 0xx−+=
2. Cho phương trình
22
2 1 40x ( m )x m m− − + − −=
với 𝑚𝑚 là tham
số. Tìm 𝑚𝑚 để phương trình có hai nghiệm phân biệt 𝑥𝑥1,𝑥𝑥2 thỏa
mãn:
( 2
điểm)
1. Ta có
( )
2
24 7 4110 9 0b ac . .∆= − = − − = >
1
75
22
b
xa
− + ∆ +3
⇒= = =
;
2
72
22
b
xa
− − ∆ −3
= = =
Phương trình có hai nghiệm phân biệt:
15x=
;
22x=
0,25
0,5
0,25
2. Ta có:
5
'
m∆=− +
Để phương trình có hai nghiệm phân biệt 𝑥𝑥1,𝑥𝑥2 thì:
0 50 5
'mm∆>⇔−+>⇔ <
Theo hệ thức Vi-et ta có:
12
2
12
22 1
42
x x m ()
x .x m m ( )
+= −
= −−
Theo đề bài ta có:
( )
( )( ) ( )
( )( )
( )
22
1 22
22 2
122
22
1 2 2 12 1 2
22
1 12 2 1 2
121 2 12
121 2
12
12
12 12
2 2 50
2 4 44 40
24 2 0
2 22 0
22 0
2 20
0
2 20 2 23
x x (x ) m m
x x xmm m
x x x xx x x
x xx x x x
xx x x xx
xx x x
x x Loai
xx
xx x x ()
− −+ − =
⇔ − + + − −− +=
⇔− + + − + =
⇔+ − − + =
⇔− + − −=
⇔ − + −=
=
−=
⇔⇔
+ −= +=
Từ (1) và (3) ta có:
12 1
12 2
22 46
2 2 42
xx m x m
xx x m
+= − = −

⇒

+= =−

Thay vào (2) ta được:
( )( )
( )( )
2
22
2
4 642 4
16 24 8 12 4
9 29 20 0
1 9 20 0
1
10 20
9 20 0 9
m mmm
m m mm m
mm
mm
m (t / m)
m
mm (t / m)
− − = −−
⇔ − − + = −−
⇔ − +=
⇔− − =
=
−=
⇔⇔
−= =
Vậy:
20
19
m ;m= =
0,25
0,25
0,25
0,25
Câu 4:
Cho đường tròn
( )
O
, bán kính
( )
>0RR
và dây cung BC cố định.
Một điểm A chuyển động trên cung lớn BC sao cho tam giác ABC có ba
( 3
điểm)
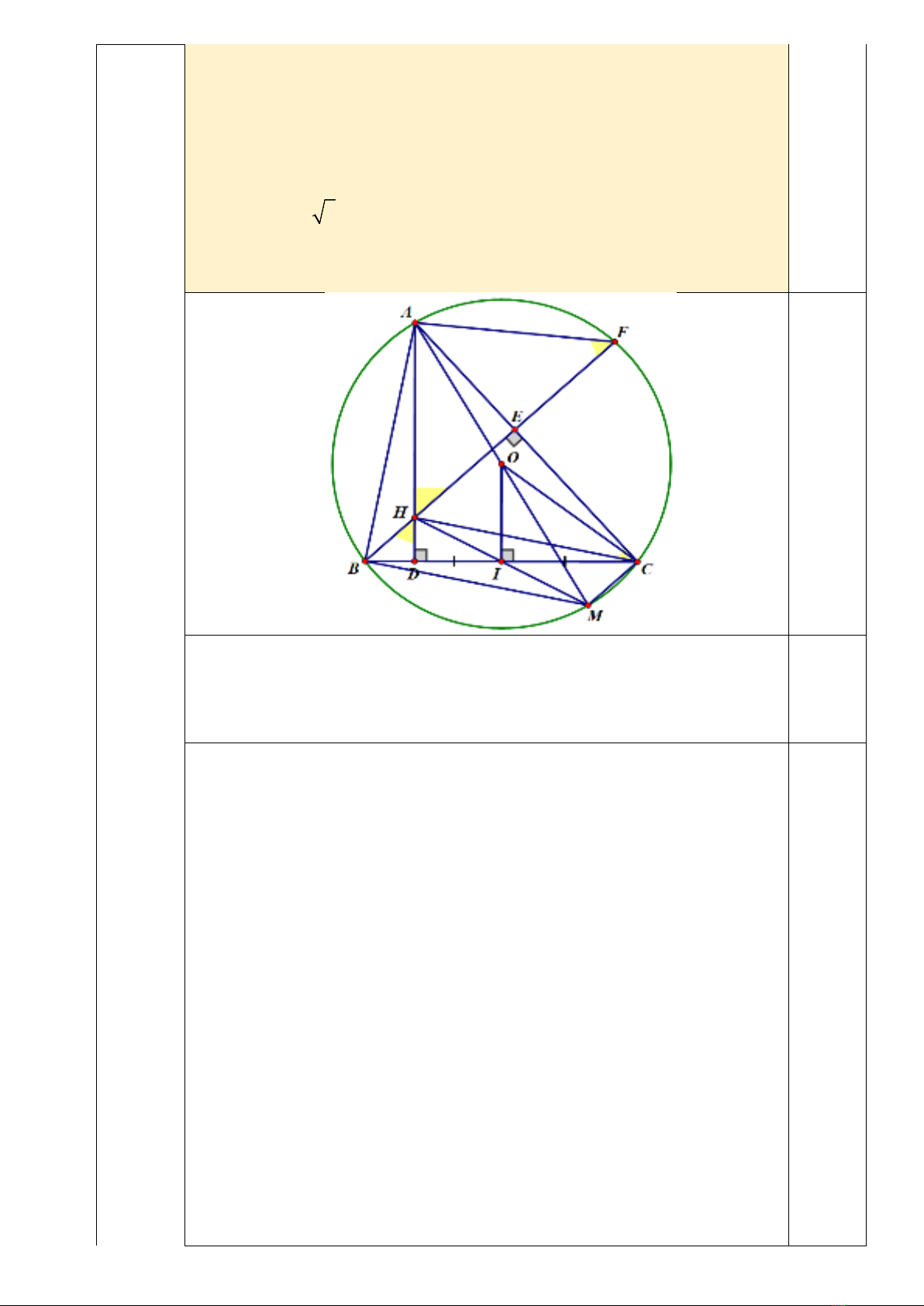
góc nhọn. Kẻ các đường cao AD, BE của tam giác ABC cắt nhau tại H và
BE cắt đường tròn
( )
O
tại F (F khác B).
1. Chứng minh rằng tứ giác DHEC nội tiếp.
2. Kẻ đường kính AM của đường tròn
( )
O
và OI vuông góc với BC
tại I. Chứng minh rằng I là trung điểm của HM và tính AF biết
=3.BC R
3. Khi BC cố định, xác định vị trí của A trên đường tròn
()O
để
DH.DA lớn nhất.
Vì
;AD BC BE AC⊥⊥
nên:
90 ; 90HDC HEC=°=°
90 90 180HDC HEC⇒ + = °+ °= °
⇒
Tứ giác DHEC nội tiếp.
Vậy: Tứ giác DHEC nội tiếp.
1đ
Trong tam giác
ABC
có
,BE AD
là hai đường cao cắt nhau tại
H
H⇒
là trực tâm tam giác
ABC
CH AB⇒⊥
Trong
( )
O
có:
ABM
,
ACM
là hai góc nội tiếp cùng chắn nửa đường tròn
đường kính
AM
.
90⇒==°ABM ACM
.
⊥
⇒⊥
MB AB
MC AC
mà
()
()
⊥
⊥
CH AB cmt
BH AC GT
Suy ra:
//MB CH
,
//MC BH
⇒BHCM
là hình bình hành
( )
1
Lại có, trong
( )
O
có
OI BC⊥
tại
I
(GT)
⇒I
là trung điểm của
BC
( )
2
(đường kính vuông góc với dây).
Từ
( )
1
và
( )
2
, suy ra
I
là trung điểm của
HM
.
Trong đường tròn
( )
O
có
ACB AFB=
( cùng chắn cung
AB
)
Lại có : Tứ giác
DHEC
nội tiếp đường tròn (c/m trên) có
DCE AHF=
(góc trong bằng góc ngoài đỉnh đối diện) hay
= ACB AHF
Suy ra
AFB AHF=
⇒∆AHF
cân tại
A
0,5
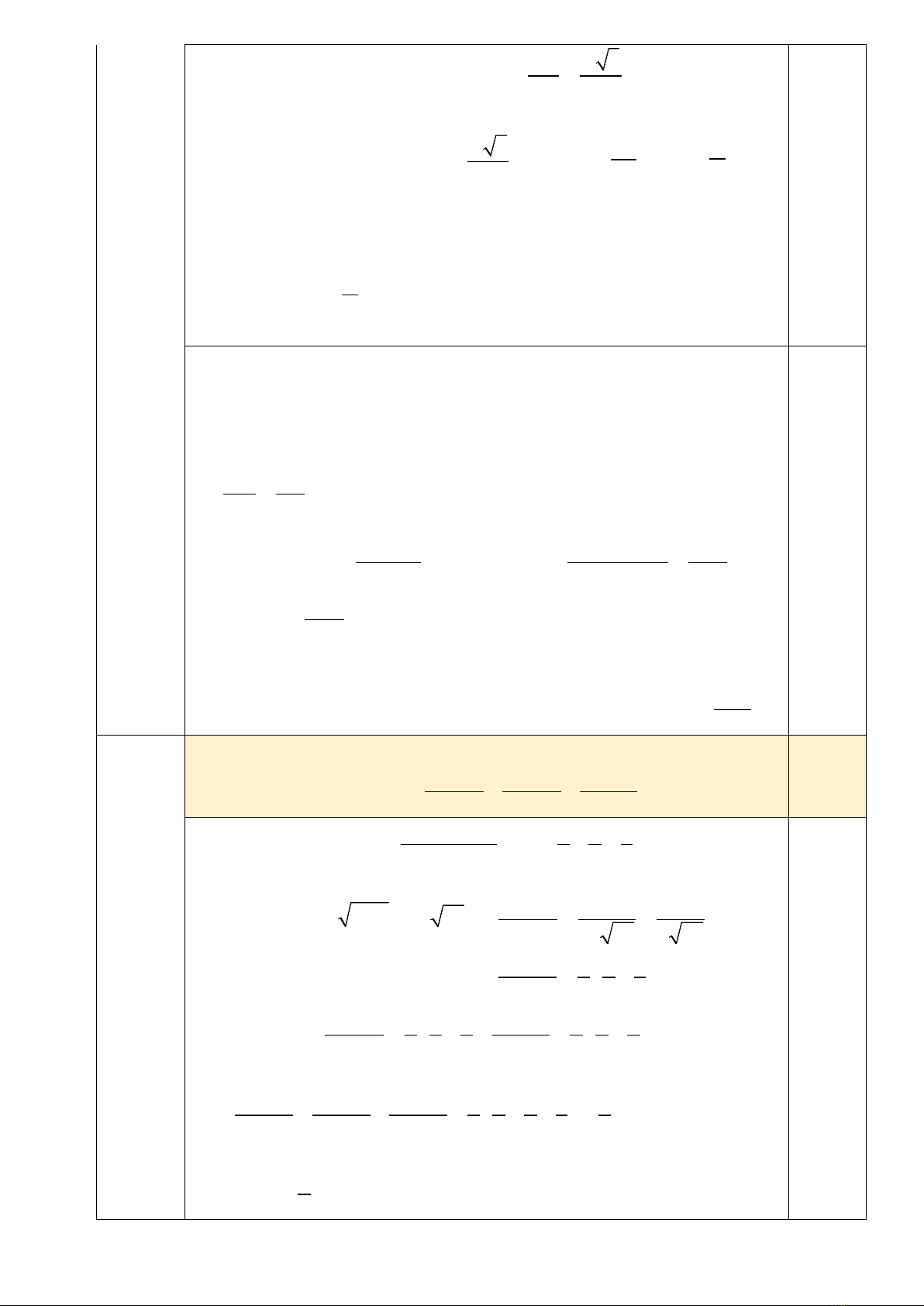
Vì
I
là trung điểm của
BC
3
22
⇒== =
BC R
BI CI
Áp dụng định lí py-ta-go vào
∆CIO
vuông tại
I
ta có:
2 22
= +OC OI CI
2
22 3
2

⇒= +


R
R OI
2
2
4
⇔=
R
OI
2
⇒=
R
OI
.
Xét
∆AHM
có:
O
là trung điểm của
AM
(GT) ,
I
là trung điểm của
HM
(c/m trên)
⇒OI
là đường trung bình của
∆AHM
.
2. 2. 2
⇒= ==
R
AH OI R
mà
AF AH=
(vì
∆AHF
cân tại
A
)
⇒=AF R
0,5
Xét
DHB∆
và
DCA∆
có
90BDH ADC= = °
(vì
AD BC⊥
)
HBD DAC=
(cùng phụ
ACB
)
(.)DHB DCA g g⇒∆ ∆∽
⇒=
DH DB
DC DA
..DH DA DB DC⇒=
Áp dụng BĐT
( )
2
4
ab
ab +
≤
, ta có:
( )
22
.44
DB DC BC
DB DC +
≤=
2
.4
BC
DH DA⇒≤
không đổi vì
BC
cố định
Dấu
""=
xảy ra khi
DB DC=
A⇔
là điểm chính giữa cung lớn
BC
Vậy
A
là điểm chính giữa cung lớn
BC
thì GTLN(
.DH DA
) =
2
4
BC
0,5
0,5
Cho
a,b,c
là ba số thực dương thỏa mãn
ab bc ca 3abc++=
. Tìm giá trị
lớn nhất của biểu thức:
2 22
abc
Ma bc b ca c ab
=++
+++
1 điểm
Câu 5
Từ điều kiện đề bài ta có
ab bc ca 1 1 1
33
abc a b c
++=⇔++=
.
Áp dụng bất đẳng thức AM-GM cho hai số dương, ta có:
22
a bc 2 a bc 2a bc+≥ =
2
a a1
a bc 2a bc 2 bc
⇒≤=
+
2
a 11 1
a bc 4 b c

⇒ ≤+

+
Tương tự, ta có
22
b 11 1 c 11 1
;
b ca 4 c a c ab 4 a b

≤+ ≤+

++

.
Cộng theo vế các bất đẳng thức trên ta được:
2 22
a b c 11 1 1 3
Ma bc b ca c ab 2 a b c 2

= + + ≤ ++ =

+++

.
Dấu “=” xảy ra a = b = c = 1
Vậy
Max
3
M a b c 1.
2
= ⇔===
1đ
Ghi chú