UBND HUYỆN CHÂU ĐỨC KỲ THI THỬ TUYỂN SINH LỚP 10 THPT NĂM HỌC 2024-2025
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO MÔN: TOÁN (CHUNG)
Thời gian làm bài: 120 phút (Không tính thời gian phát đề)
ĐỀ CHÍNH THỨC
Bài 1. (2.5 điểm)
a) Rút gọn các biểu thức sau:
32212
A
và
3
6
32
3
B
.
b) Giải các phương trình
0232
2
xx
.
c) Giải hệ phương trình sau
96
14
yx
yx
.
Ba:i 2. (1,5 điểm)
a) Vẽ đồ thị (P) của hàm số
2
2
1xy
và đường thẳng (d)
1
2
1 xy
trên cùng một hệ trục toạ độ.
b) Tìm toạ độ các giao điểm của (P) và (d) bằng phép toán.
Ba:i 3. (2,0 điểm)
a) Hai người thợ cùng quét sơn một ngôi nhà thì trong 6 ngày xong việc. Nếu họ làm riêng thì người
thợ thứ nhất hoàn thành công việc chậm hơn người thợ thứ hai là 9 ngày. Hỏi nếu làm riêng thì mỗi
người thợ phải làm trong bao nhiêu ngày để xong việc.
b) Tìm m để phương trình
012 22 mmmxx
có hai nghiệm x1, x2 thỏa mãn
5,4
2
1
2
2
1 mxx
.
c) Giải các phương trình
5433 22 xxxx
.
Bài 4. (3,5 điểm) Cho đường tròn (O). Đường thẳng (d) không đi qua tâm (O) cắt đường tròn tại hai
điểm A và B, C là điểm thuộc (d) ở ngoài đường tròn (O) sao cho A nằm giữa C và B. Vẽ đường kính
MN vuông góc với dây AB tại D (M thuộc cung lớn AB), Tia CM cắt đường tròn (O) tại điểm thứ hai là
I, IN cắt AB tại K.
a) Chứng minh tứ giác MDKI nội tiếp đường tròn.
b) Chứng minh CI.CM = CK.CD.
c) Chứng minh IC là phân giác của góc ngoài ở đỉnh I của tam giác AIB.
d) Cho ba điểm A, B, C cố định. Đường tròn (O) thay đổi nhưng vẫn đi qua A và B. Chứng minh rằng
IN luôn đi qua một điểm cố định.
Bài 5. (0,5 điểm) Cho hai số dương x, y thỏa mãn đẳng thức
. Tìm giá trị lớn nhất của biểu
thức
224224 2
1
2
1
yxxyxyyx
P
.
---------Hết--------
Thí sinh không được sử dụng tài liệu, cán bộ coi thi không giải thích gì thêm
Họ và tên thí sinh: ………………………………..
Số báo danh:………………………………………
Chữ ký của CBCT số 1: ………………………………....
Chữ ký của CBCT số 2: …………………………………
UBND HUYỆN CHÂU ĐỨC
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM ĐỀ THI THỬ LỚP 10 THPT NĂM HỌC 2024-2025
MÔN: TOÁN (CHUNG)
Bài 1: (2.5 điểm)
a) Rút gọn các biểu thức sau:
32212
A
và
3
6
32
3
B
.
b) Giải các phương trình
0232 2 xx
. c) Giải hệ phương trình sau
96
14
yx
yx
.
Bài Nội dung Điểm
1
(2,5đ) a)
3243223232212
A
0.25x2
332332
3
6
32
3
B
0.25x2
b)
025
0.25
Tìm được
2
1
;2 21
xx
0.25x2
c)
3
1
14
1
14
1010
96
14
y
x
y
x
yx
x
yx
yx
0.25x3
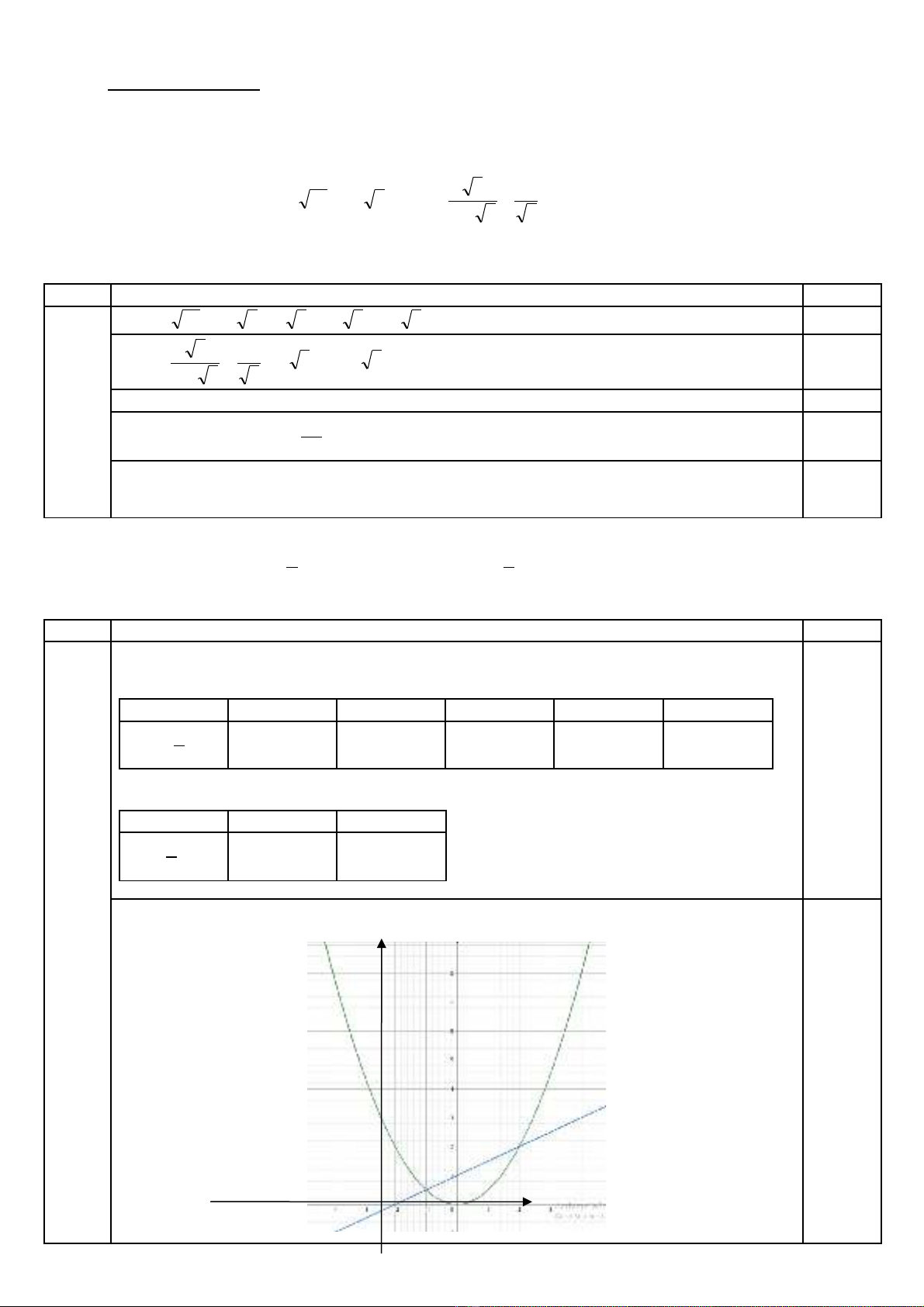
Ba:i 2. (1,5 điểm)
a) Vẽ đồ thị (P) của hàm số
2
2
1xy
và đường thẳng (d)
1
2
1 xy
trên cùng một hệ trục toạ độ.
b) Tìm toạ độ các giao điểm của (P) và (d) bằng phép toán.
Bài Nội dung Điểm
2
(1,5đ) a) - Lập bảng giá trị đúng 3/5 điểm đạt 0.5 điểm
- Lập bảng giá trị đúng 1/5 điểm đạt 0.25 điểm
x
- 4 - 2 0 2 4
2
2
1xy
8 2 0 2 8
- Lập bảng giá trị đúng 1/2 điểm đạt 0.25 điểm
x
0 - 2
1
2
1
xy
1 0
0.5
Vẽ đúng cả hai đồ thị đạt thêm 0.5 điểm (Không có bảng giá trị mà vẽ đúng hai đồ thị vẫn
đat 1,0đ)
0.5
x
y(P)
(d)
b) PTHĐGĐ của (P) và (d) là :
1
2
1
2
1
2
xx
0.25
2;102
21
2
xxxx
Với
2
1
1
2
1
1
2
11
yx
Với
22.
2
1
2
2
12
yx
Vậy tọa độ giao điểm của (P) và (d) là
2
1
;1
và
2;2
.0.25
Ba:i 3. (2,0 điểm)
a) Hai người thợ cùng quét sơn một ngôi nhà thì trong 6 ngày xong việc. Nếu họ làm riêng thì người thợ thứ
nhất hoàn thành công việc chậm hơn người thợ thứ hai là 9 ngày. Hỏi nếu làm riêng thì mỗi người thợ phải làm
trong bao nhiêu ngày để xong việc.
b) Tìm m để phương trình
012 22 mmmxx
có hai nghiệm x1, x2 thỏa mãn
5,4
2
1
2
2
1
mxx
.
c) Giải các phương trình
5433 22 xxxx
.
Bài Nội dung Điểm
3
(2,0đ)
a) Gọi x (ngày) là thời gian người thợ thứ hai hoàn thành công việc một mình (x > 6) 0.25
Thời gian người thợ thứ nhất hoàn thành công việc một mình là x + 9 (ngày)
Trong 1 ngày:
- Người thợ thứ nhất làm được
9
1
x
(công việc)
- Người thợ thứ hai làm được
x
1
(công việc)
- Cả hai người thợ làm được
6
1
(công việc)
0.25
Từ đó ta có phương trình
6
11
9
1
xx
0.25
Giải pt ta được:
9
x
(n);
6
x
(l)
Vậy người thợ thứ hai hoàn thành công việc một mình là 9 ngày; người thứ nhất là 18
ngày.
0.25
b) Để phương trình
012 22 mmmxx
có hai nghiệm x1, x2 thì
01
/
m
1 m
0.25
Theo Vi-ét ta có:
1.
2
2
21
21
mmxx
mxx
Theo đề ta có:
9925,4
2
1
221
2
12
2
12
2
1
xxxxmxxmxx
010391499
222
21
2
21
2
221
2
1
mmmmmxxxxxxxx
)(2;)(
3
5
21
lmnm
Vậy
3
5
m
0.25
c)
5433 22 xxxx
(*)
Đặt
txx 3
2
5;10545)4.((*) 21
2 ttttttPt
0.25
*
2
133
;
2
133
013131 21
22
1
xxxxxxtt
*
ptvnxxxxtt 053535 22
2
Vậy pt(*) có hai nghiệm phân biệt là
2
133
;
2
133
21
xx
0.25
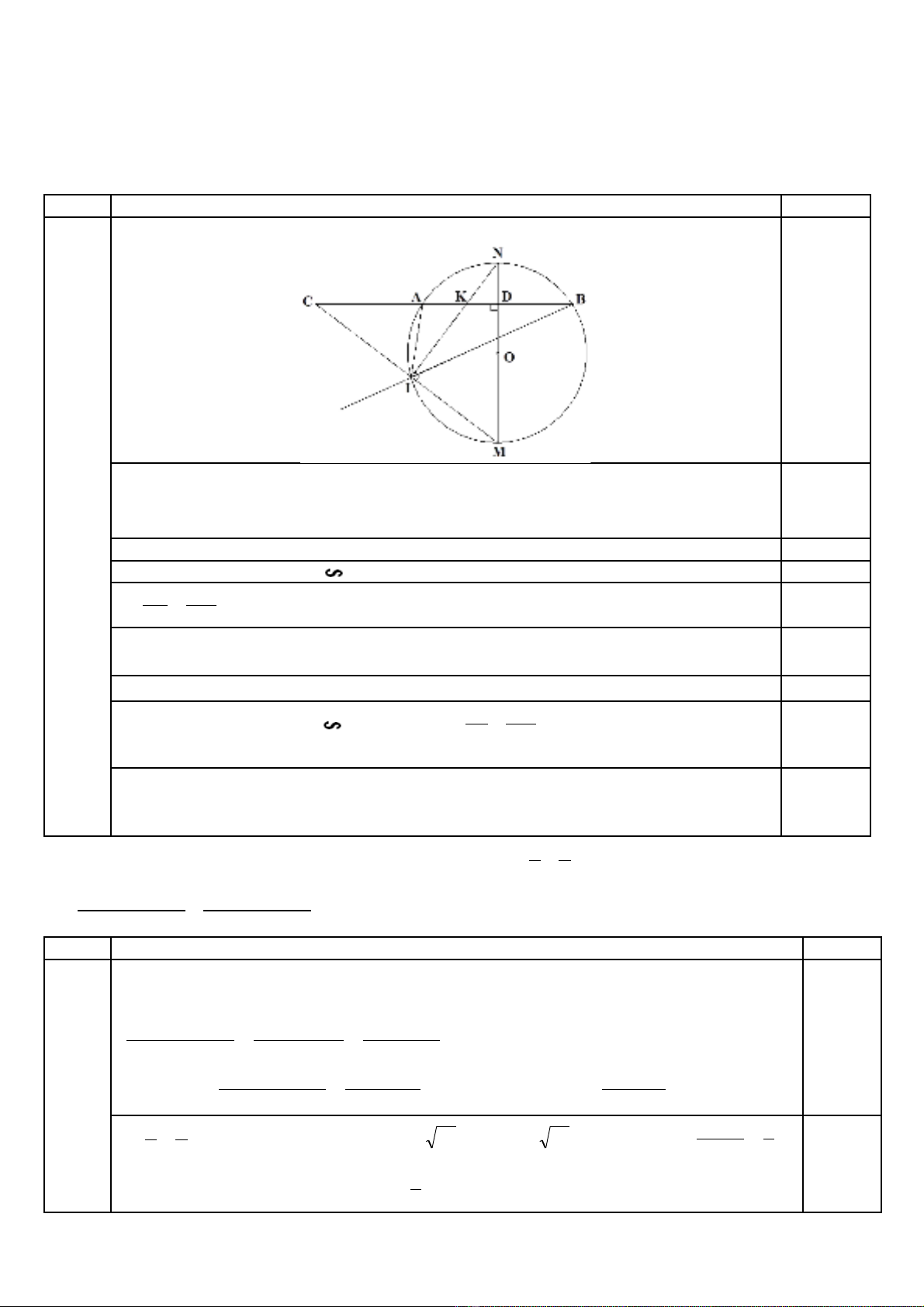
Bài 4. (3,5 điểm) Cho đường tròn (O). Đường thẳng (d) không đi qua tâm (O) cắt đường tròn tại hai điểm A và
B, C là điểm thuộc (d) ở ngoài đường tròn (O) sao cho A nằm giữa C và B. Vẽ đường kính MN vuông góc với
dây AB tại D (M thuộc cung lớn AB), Tia CM cắt đường tròn (O) tại điểm thứ hai là I, IN cắt AB tại K.
a) Chứng minh tứ giác MDKI nội tiếp đường tròn. b) Chứng minh CI.CM = CK.CD.
c) Chứng minh IC là phân giác của góc ngoài ở đỉnh I của tam giác AIB.
d) Cho ba điểm A, B, C cố định. Đường tròn (O) thay đổi nhưng vẫn đi qua A và B. Chứng minh rằng IN luôn đi
qua một điểm cố định.
Bài Nội dung Điểm
4
(3,5đ)
Vẽ hình đúng đạt 0.5 điểm
0.5
a) Tứ giác MDKI, có:
0
90
ˆKIM
(góc nội tiếp chắn nữa đường tròn)
0
90
ˆKDM
(gt)
0.5-0.25
Vậy tứ giác MDKI nội tiếp đường tròn đường kính MK 0.25
b) Chứng minh được
CIK
CDM
(g-g) 0.5
CDCKCMCI
CM
CK
CD
CI ..
0.25x2
c) Ta có:
nên N là trung điểm của cung AB suy ra cung NA bằng cung NB
NIBNIA ˆˆ
IN
là tia phân giác của
BIAˆ
0.25
mà
INIC
nên
IC
là phân giác của góc ngoài ở đỉnh I của tam giác AIB. 0.25
d) Chứng minh được
CIB
CAM
(g-g)
CBCACMCI
CM
CB
CA
CI ..
mà
CDCKCMCI ..
(cmt) nên
CBCACDCK ..
0.25
Do
CBA ,,
cố định và
DABMN
nên D cũng cố định
mà
CBCACDCK ..
nên K cố định
Vậy IN luôn đi qua một điểm cố định.
0.25
Bài 5. (0,5 điểm) Cho hai số dương x, y thỏa mãn đẳng thức
2
11
yx
. Tìm giá trị lớn nhất của biểu thức
224224
2
1
2
1
yxxyxyyx
P
.
Bài Nội dung Điểm
1
(2,5đ) Với
0;0
yx
ta có:
22224224224
2
2
2222020 xyyxxyyxyxyxyyxxyx
)1(
2
1
22
1
2
1
22224
yxxyxyyxxyyx
Tương tự có
)2(
2
1
2
1
224
yxxyyxxy
. Từ (1) và (2)
yxxy
P
1
0.25
Vì
xyyx
yx 22
11
mà
2
1
2
1
1222
2
xy
Pxyxyxyxyyx
Vậy giá trị lớn nhất của biểu thức P là
1
2
khi
1
yx
0.25
(Cách giải đúng khác vẫn cho điểm tối đa)