SỞ GIÁO DỤC VÀ ĐÀO T
ẠO
( Đề chính thức)
Trường THPT Nghĩa Lộ
ĐỀ THI THỬ TỐT NGHIỆP THPT
NĂM HỌC 2012
Môn: TOÁN
Đề thi gồm: 01 trang Thời gian làm bài: 150 phút
(không kể thời gian giao đề)
I. PHẦN CHUNG DÀNH CHO TẤT CẢ CÁC THÍ SINH (7,0 điểm)
Câu 1 (3,0 điểm). Cho hàm số
1
1
x
x
y
1) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
2) Tính diện tích hình phẳng giới hạn bởi (C), trục Ox và các đường thẳng x=1, x=3.
Câu 2 (3,0 điểm)
1) Giải phương trình 02)1(log)1(log4 2
2
4 xx trên tập số thực.
2) Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 15)( 23 xxxxf trên
3;0 .
3) Tính tích phân: 2
0
(2 1).sin
I x xdx
Câu 3 (1,0 điểm). Cho hình chóp tứ giác đều ABCDS. biết aAB
, góc giữa mặt bên
và đáy bằng 600. Tính thể tích của khối chóp ABCDS..
II. PHẦN RIÊNG (3,0 điểm)
Thí sinh chỉ được chọn một trong hai phần sau ( phần 1 hoặc phần 2).
1. Theo chương trình Chuẩn:
Câu 4a (2,0 điểm). Trong không gian Oxyz cho điểm )4;2;4(
Avà đường thẳng (d)
có phương trình
4
1
1
1
2
3
zyx .
1) Viết phương trình mặt phẳng )(P qua điểm
A
và vuông góc với đường thẳng (d).
2) Tìm toạ độ điểm
A
đối xứng với điểm
A
qua đường thẳng (d).
Câu 5a (1,0 điểm) Giải phương trình 0532 2 zz trên tập số phức.
2. Theo chương trình Nâng cao:
Câu 4b (2,0 điểm). Trong không gian Oxyz cho mặt phẳng )(
và đường thẳng (d) có
phương trình: )(
:0122
zyx và (d):
2
2
1
1
1
zyx
1) Gọi
A
là giao điểm của đường thẳng (d) với mặt phẳng )(
, hãy viết phương trình
tham số của đường thẳng OA
2) Tìm điểm
M
thuộc đường thẳng (d) sao cho khoảng cách từ điểm
M
đến mặt
phẳng )(
bằng 2.
Câu 5b (1,0 điểm). Giải phương trình 03)2(
2 iziz trên tập số phức.
............ Hết ..............
HƯỚNG DẪN CHẤM
Bản hướng dẫn gồm có 04 trang
A. Phần
chung ĐÁP ÁN ĐIỂM
Câu 1
(3,0 điểm)
1. (2,0 điểm)
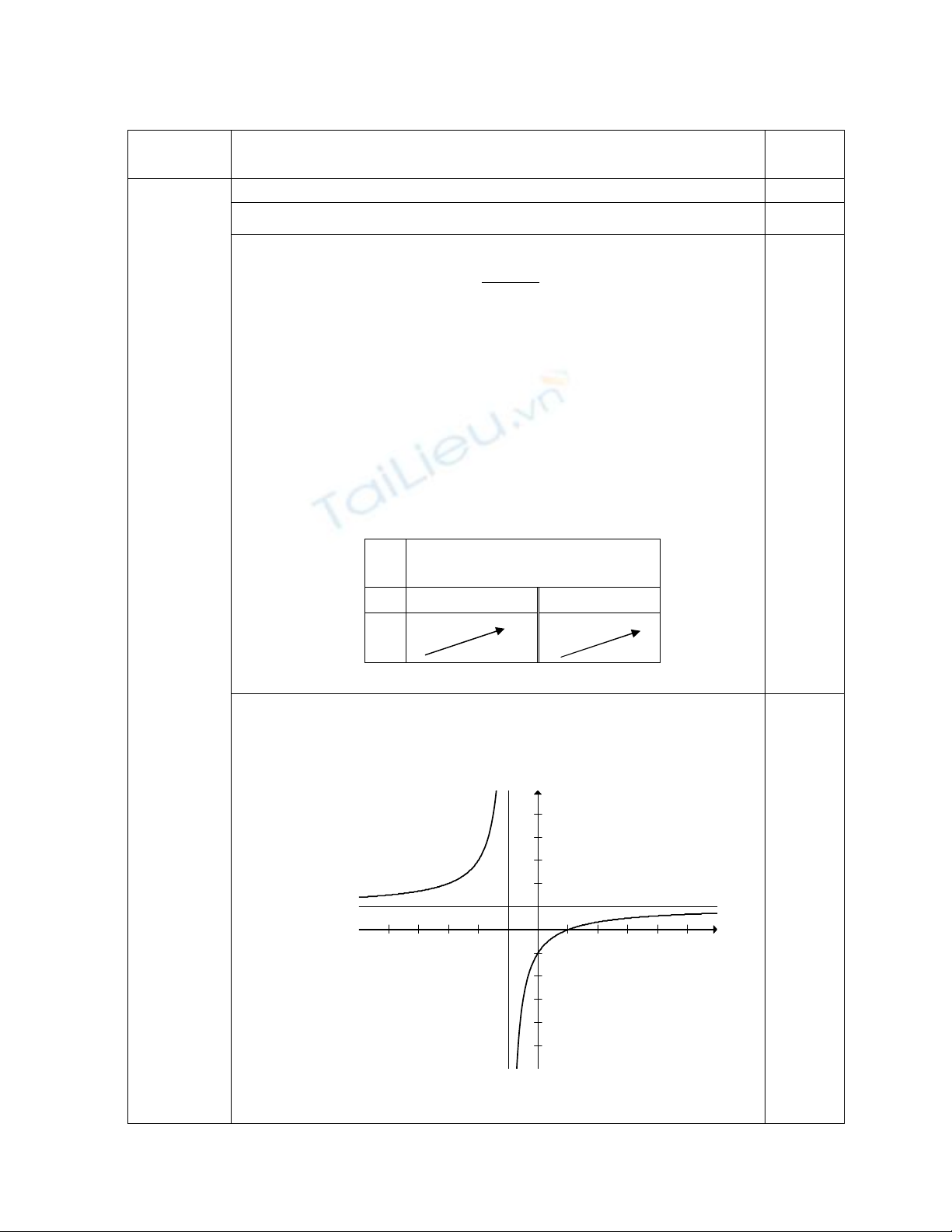
a) Tập xác định: D =
1\R 0,25
b) Sự biến thiên
+) Chiều biến thiên: có 2
'
)1(
2
x
y> 0 với xD
Hàm số đồng biến trên mỗi khoảng
1; và
;1
+) Cực trị: Hàm số đã cho không có cực trị
+) Giới hạn và tiệm cận:
1lim
 y
x, 1lim
 y
x
Suy ra, đồ thị hàm số có tiệm cận ngang là đường thẳng y=2

y
x
lim
)1(
, 
y
x
lim
)1(
Suy ra, đồ thị hàm số có tiệm cận đứng là đường thẳng x=1
+) Bảng biến thiên
x

-1

y
’
+ +
y

1 1

0,25
0,25
0,25
0,25
0,25
c) Đồ thị
Đồ thị cắt trục tung tại điểm
1;0
Đồ thị cắt trục hoành tại điểm
0;1
0,5
-5 -4 -3 -2 -1 1 2 3 4 5
-5
-4
-3
-2
-1
1
2
3
4
5
x
y
0
y=1
x = - 1
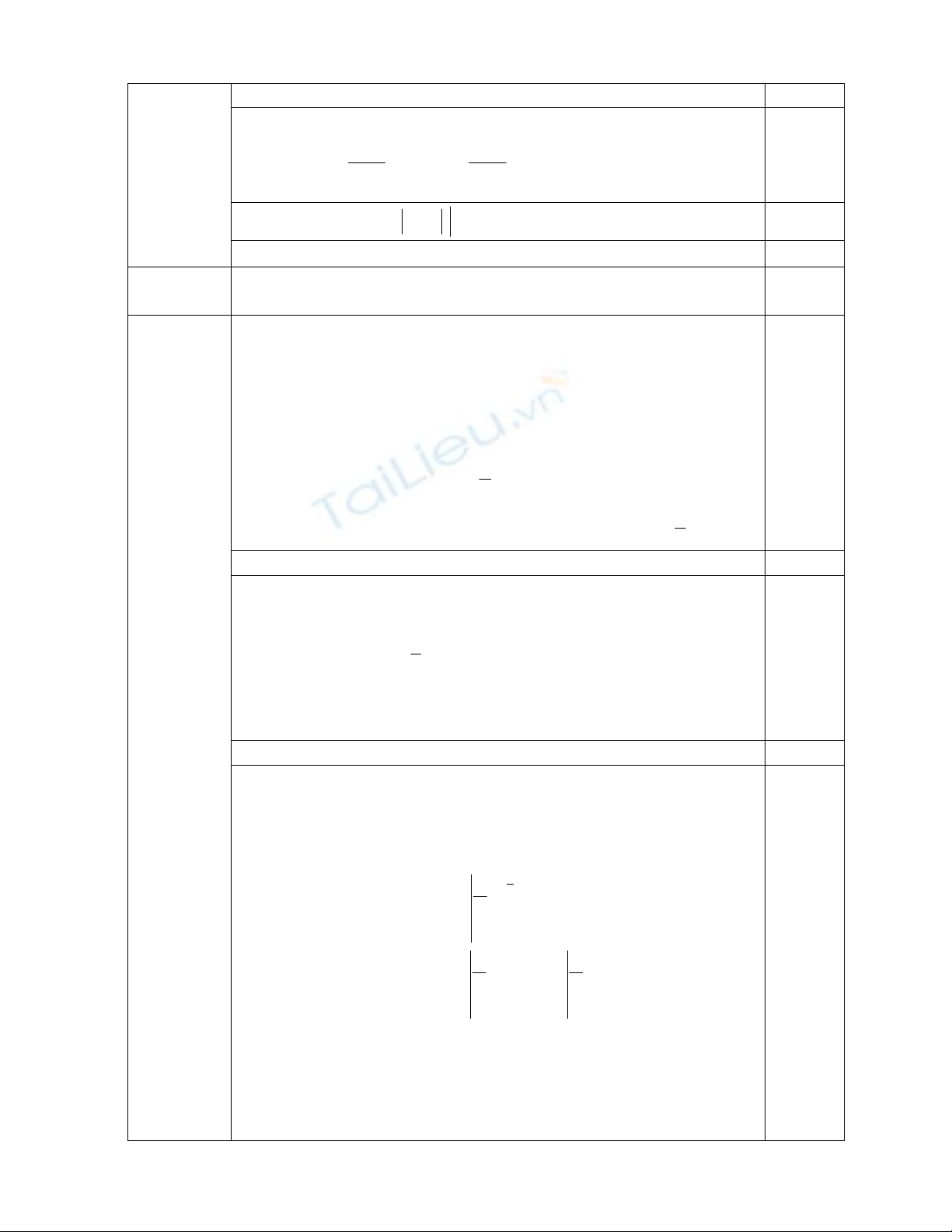
2. (1,0điểm )
Diện tích hình phẳng cần tìm là
S= dx
x
dx
x
x
3
1
3
11
2
1
1
1
0,25
3
1
1ln2 xx 0,5
4ln2)2ln21()4ln23(
0,25
Câu 2
(3,0 điểm)
1. (1,0 điểm)
+) ĐK x > -1
+) Ta có 02)1(log)1(log4 2
2
4 xx
02)1(log)1(log 2
2
2 xx
2)1(log
1)1(log
2
2
x
x
4
3
1
x
x
thoả mãn điều kiện
Vậy phương trình đã cho có hai nghiệm là ,1
x
4
3
x
0,25
0,25
0,25
0,25
2.( 1,0 điểm)
+) Ta có 523)(' 2 xxxf
+)
3
5
1
0)(' x
x
xf Trên
3;0 có 10)('
xxf
+) 1)0(
f, 2)1(
f, 22)3(
f
+) Vậy
22)3()(
3;0 fxfMax ,
2)1()(
3;0 fxfMin
0,25
0,25
0,25
0,25
3.(1,0 điểm)
+) Đặt 2 1 2
sin cos
u x du dx
dv xdx v x
+) Ta được I = xx cos)21(
0
2
xdx
2
0
cos2
= xx cos)21(
0
2
xsin2
0
2
=1
0,5
0,5
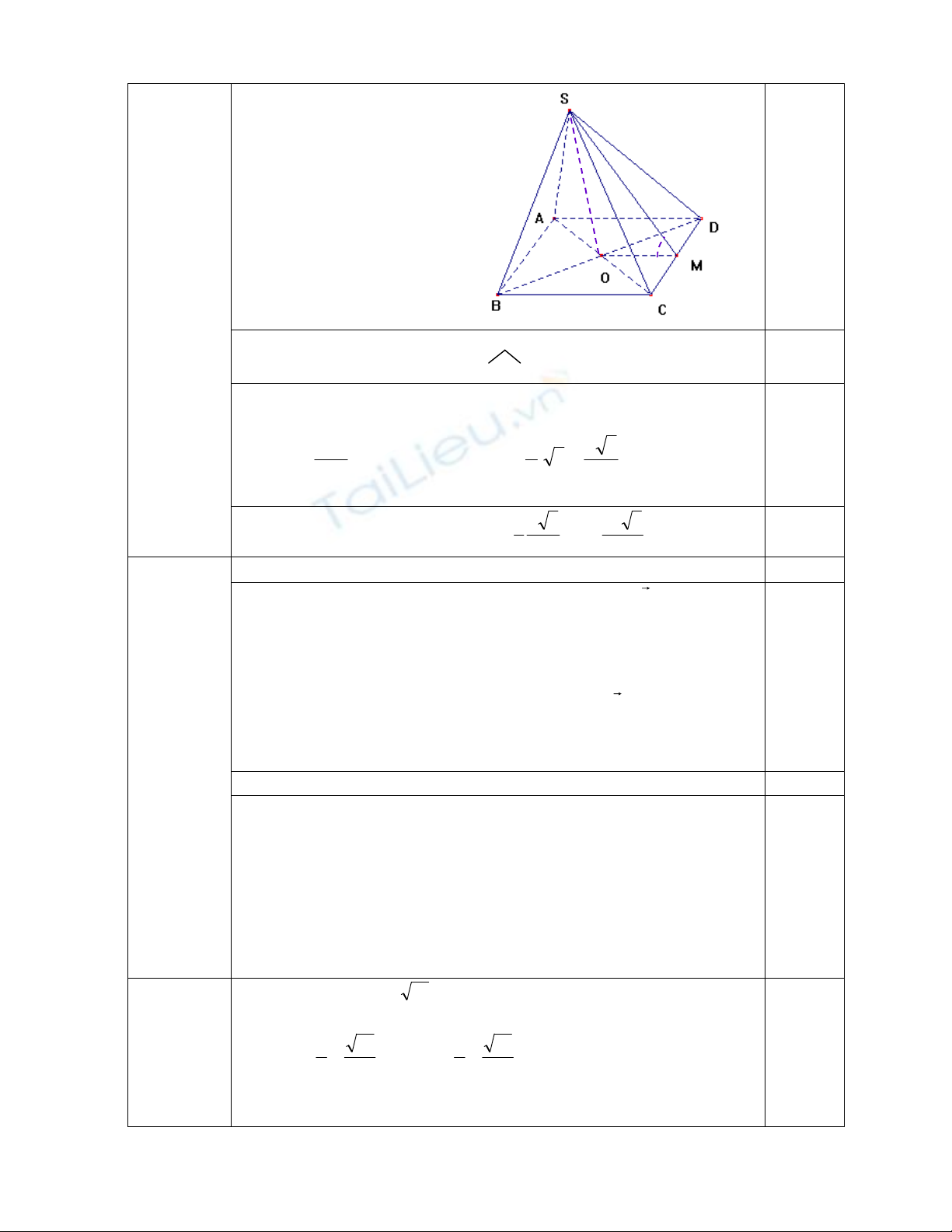
Câu 3
(1,0 điểm)
+) Gọi BDACO
,
M
là trung điểm của CD
Ta có CDSMCDOM
,=> 0
60SMO
0,25
+) Vì hình chóp ABCDS. là hình chóp đều suy ra SO là đường
cao của hình chóp . Trong tam giác vuông SOM ta có
OM
SO
0
60tan =>
2
3
3.
2
60tan. 0aa
OMSO
+) Diện tích đáy của hình chóp bằng 2
a
0,25
0,25
+) Thể tích của khối chóp là:
6
3
.
2
3
3
13
2a
a
a
V 0,25
B. Phần
riêng
Câu 4a
(2,0 điểm)
1. (1,0 điểm)
+) Đường thẳng (d) có một véc tơ chỉ phương là )4;1;2( u
+) Vì mặt phẳng )(Pvuông góc với đường thẳng (d), nên véc
tơ chỉ phương của đường thẳng (d) là véc tơ pháp tuyến của
mặt phẳng )(P
+) Mặt phẳng )(P qua điểm )4;2;4(
Anhận )4;1;2( u là véc
tơ pháp tuyến nên phương trình của mặt phẳng )(P là
0)4(4)2(1)4(2
zyx 01042
zyx
0,25
0,25
0,5
2. ( 1,0 điểm)
+) gọi )(PdH
suy ra toạ độ
H
là nghiệm của hệ
tz
ty
tx
zyx
41
1
23
01042
=> )3;0;1(1

Ht
+) Điểm
A
đối xứng với điểm
A
qua đường thẳng (d)
suy ra )2;2;2('A
0,5
0,5
Câu 5a
(1,0 điểm)
+) Ta có
31
=( 31 i)
2
+) Suy ra, phương trình có hai nghiệm là
iz
4
31
4
3
1 và iz
4
31
4
3
2
0,5
0,5
Câu 4b
(2,0 điểm)
1. ( 1,0 điểm )
+) Tìm được toạ độ của điểm
1;2;
2
3
A
+) Đường thẳng OA nhận
1;2;
2
3
OA là một véc tơ chỉ
phương nên phương trình tham số của đường thẳng OA là
tz
ty
tx
2
2
3
0,5
0,5
2. (1,0 điểm )
+) )(dM
=> )2;21;1( tttM
+) Khoảng cách từ điểm
M
đến mặt phẳng )(
là
3
42
212
1)2(2)21()1(2
222
tttt
d
+) Khoảng cách từ điểm
M
đến mặt phẳng )(
bằng 2
2
1
2
3
42
t
t
t
+) Vậy được hai điểm thoả mãn điều kiện đầu bài là
)2;1;0(
1M và )4;5;3(
2M
0,25
0,25
0,25
0,25
Câu 5b
(1,0 điểm)
+) Ta có
9
=( i3)
2
+) Phương trình đã cho có hai nghiệm
i
ii
z21
2
32
1
và i
ii
z
1
2
32
2
0,5
0,5
-------------------Hết-----------------