SỞ GIÁO DỤC PHÚ THỌ
ĐỀ THAM KHẢO
KÌ THI TUYỂN SINH VÀO LỚP 10 THPT
NĂM HỌC 2022-2023
Bài thi: TOÁN
Thời gian làm bài 120 phút, không kể thời gian phát đề
GV giải đề: Vũ Hưng – Nguyễn Quang
Đề có 02 trang
LỜI GIẢI CHI TIẾT THAM KHẢO
THCS.TOANMATH.com
Phần I. Trắc Nghiệm Khách Quan (2,5 điểm)
Câu 1. Kết quả rút gọn biểu thức
2
4 3 7
A.
4 3 7.
B.
7 4 3.
C.
D.
3 3.
Câu 2. Trong các hàm số sau, hàm số nào là hàm số bậc nhất nghịch biến trên
?
A.
2
2.yx
B.
5 (3 ).yx
C.
2 7.yx
D.
3 4 .yx
Câu 3. Cho đường thẳng
: 2 4.d y x
Gọi
,AB
lần lượt là giao điểm của
d
với trục
hoành và trục tung. Diện tích
OAB
bằng
A.
3.
B.
2.
C.
4.
D.
8.
Câu 4. Khi
1m
hệ phương trình
2
23
6
mx y
m x y


có nghiệm
;xy
là
A.
15;9 .
B.
3;3 .
C.
9;3 .
D.
15;9 .
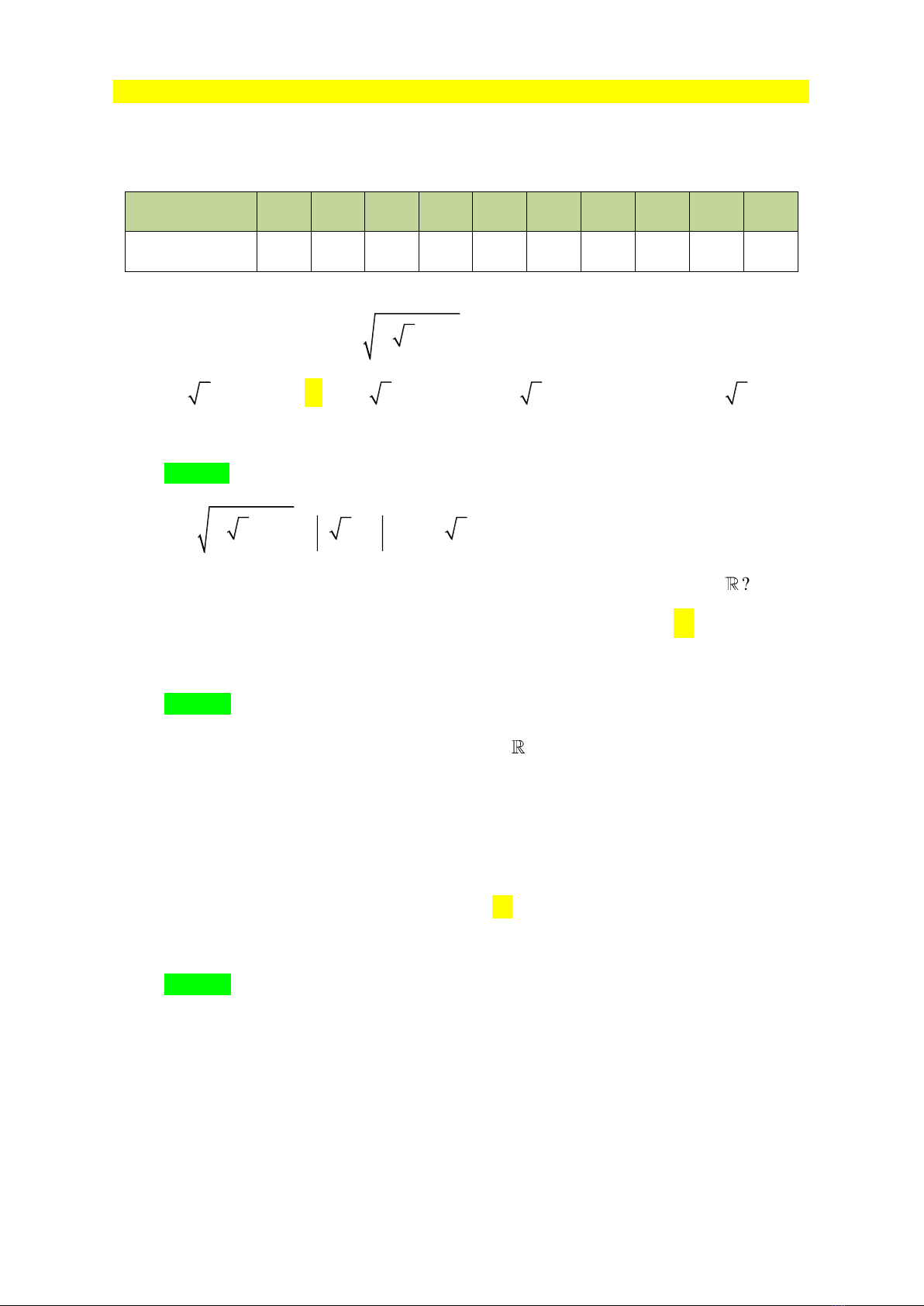
Câu 5. Đồ thị của hình bên là đồ thị của hàm số nào trong các hàm số sau?
A.
2
4.x
B.
2
2.yx
C.
2
1.
4
yx
D.
2
1.
2
yx
Câu 6. Gọi
12
,xx
là hai nghiệm của phương trình
25 3 0.xx
Khi đó
1 2 1 2
x x x x
bằng
A.
8.
B.
2.
C.
8.
D.
2.
Câu 7. Điều kiệnc của
m
để phương trình
270x mx
có hai nghiệm phân biệt là
A.
27m
hoặc
2 7.m
B.
2 7.m
C.
2 7 2 7.m
D.
2 7.m
Câu 8. Cho
ABC
vuông tại
A
có
12AB cm
và
1
tan .
3
B
Độ dài cạnh
AC
là
A.
36 .cm
B.
8 2 .cm
C.
24 2 .cm
D.
4.cm
Câu 9. Trên một cái thang dài
3,5m
người ta ghi: “ Để đảm bảo an toàn khi sử dụng, phải
đặt thang tạo với mặt đất một góc có độ lớn từ
60
đến
70
”. Gọi
,xm
0x
là
khoảng cách từ chân thang đến chân tường. Để đảm bảo an toàn khi sử dụng thì điều
kiện của
x
là
A.
1,2 1,75.x
B.
1,2 1,75.x
C.
1,2.x
D.
1,75.x
Câu 10. Cho tam giác nhọn
ABC
nội tiếp đường tròn tâm
.O
Các cung nhỏ
,,AB BC CA
có số đo lần lượt là
75 ;2 26 ;3 23x x x
. Số đo
ACB
của
ABC
là
A.
47 .
B.
60 .
C.
61 .
D.
59 .
Phần II. Tự Luận (7,5 điểm)
Câu 1 (1,5 điểm). Cho biểu thức
1 1 2
.
444
xx
Pxx x x





với
0, 4.xx
a) Tính giá trị của biểu thức
P
khi
9.x
b) Rút gọn biểu thức
.P
c) Tìm
x
để
1.P
Câu 2 (2,0 điểm). Cho parabol
2
:P y x
và đường thẳng
: 3 2.d y mx
a) Viết phương trình đường thẳng đi qua hai điểm
A
và
.B
Biết hai điểm
A
và
B
đều thuộc parabol
P
có hoành độ lần lượt là
1;2.
b) Tìm
m
để đường thẳng
d
cắt parabol
P
tại hai điểm phân biệt
11
;;C x y
22
;D x y
sao cho
22
2 1 2 1
10T y y x x
đạt giá trị nhỏ nhất.
Câu 3 (3,0 điểm). Cho đường tròn
O
và dây
BC
không đi qua
.O
Điểm
A
thuộc cung
lớn
BC
(
A
khác
,BC
),
M
là điểm chính giữa cung nhỏ
.BC
Hai tiếp tuyến của
O
tại
C
và
M
cắt nhau ở
.N
Gọi
K
là giao điểm của đường thẳng
AB
và
,CM
tia
AM
cắt tia
CN
tại
,P
hai đoạn thẳng
AM
và
BC
cắt nhau tại
.Q
Chứng minh rằng
a) Tứ giác
nội tiếp đường tròn
b)
MN
song song với
.BC
c)
1 1 1 .
CN KP CQ

Câu 4 (1,0 điểm). Giải hệ phương trình sau
2
2
7 4 3 1 .
2 3 2
xy
y xy x
………. Hết………..
ĐÁP ÁN CHI TIẾT ĐỀ MINH HỌA VÀO LỚP 10 THPT NĂM HỌC 2022-2023
Phần I. Trắc Nghiệm Khách Quan (2,5 điểm)
BẢNG ĐÁP ÁN
Câu
1
2
3
4
5
6
7
8
9
10
Đáp án
B
D
C
A
B
C
A
D
B
C
Câu 1. Kết quả rút gọn biểu thức
2
4 3 7
A.
4 3 7.
B.
7 4 3.
C.
3 3.
D.
3 3.
Lời giải
Chọn B.
Ta có:
2
4 3 7 4 3 7 7 4 3.
Câu 2. Trong các hàm số sau, hàm số nào là hàm số bậc nhất nghịch biến trên
?
A.
2
2.yx
B.
5 (3 ).yx
C.
2 7.yx
D.
3 4 .yx
Lời giải
Chọn D.
Để hàm số
y ax b
nghịch biến trên khi và chỉ khi:
0.a
Vậy hàm số:
34yx
nghịch biến vì
4 0.a
Câu 3. Cho đường thẳng
: 2 4.d y x
Gọi
,AB
lần lượt là giao điểm của
d
với trục
hoành và trục tung. Diện tích
OAB
bằng
A.
3.
B.
2.
C.
4.
D.
8.
Lời giải
Chọn C.
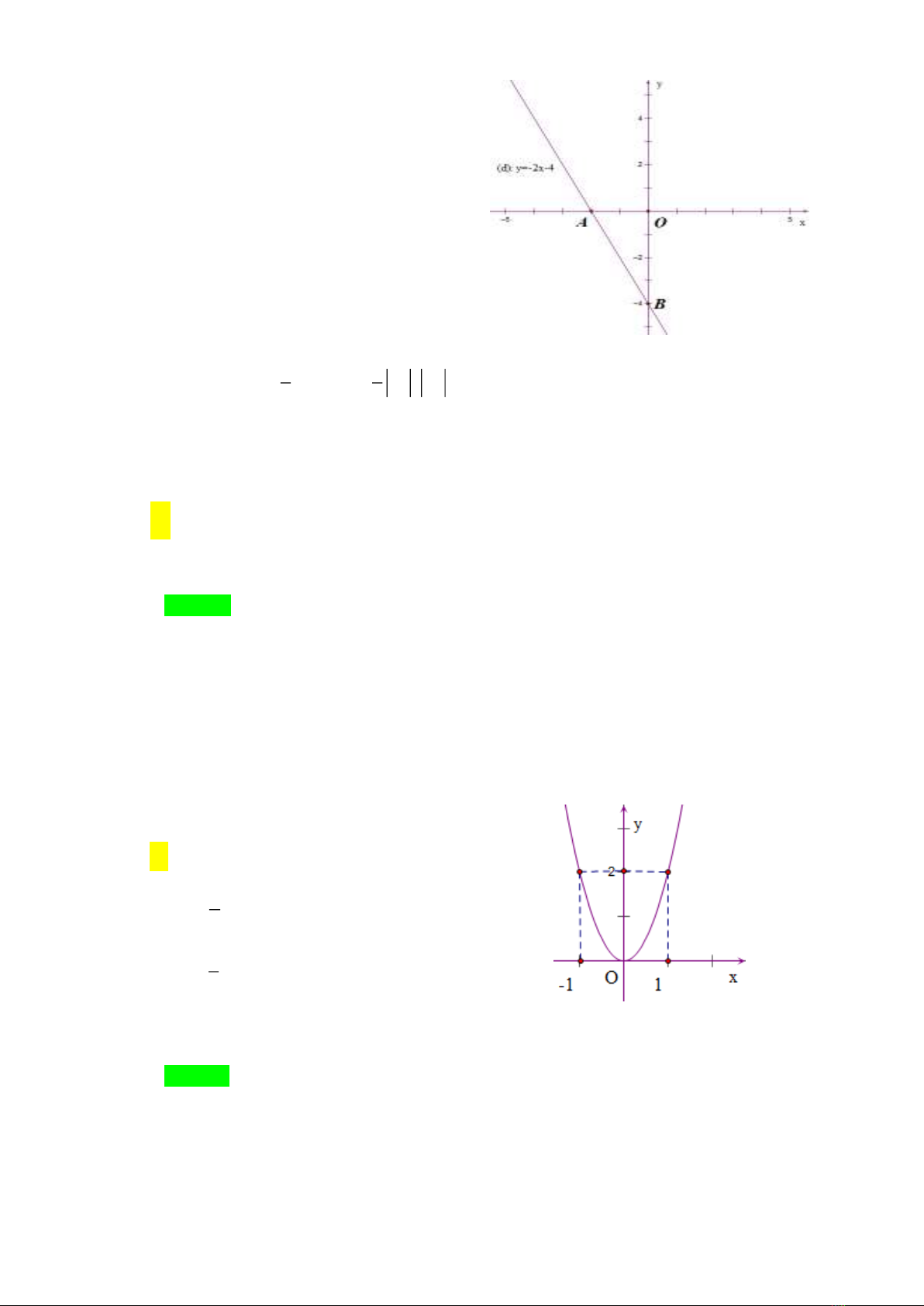
0
: 2;0 .
2
y
d Ox A
x

0
: 0; 4 .
4
x
d Oy B
y

Ta có:
11
. 2 . 4 4 .
22
OAB
S OAOB dvdt
Câu 4. Khi
1m
hệ phương trình
2
23
6
mx y
m x y


có nghiệm
;xy
là
A.
15;9 .
B.
3;3 .
C.
9;3 .
D.
15;9 .
Lời giải
Chọn A.
Thay
1m
vào hệ ta được:
23
.
6
xy
xy

Bấm máy tính casio ta được nghiệm hệ:
; 15;9 .xy
Câu 5. Đồ thị của hình bên là đồ thị của hàm số nào trong các hàm số sau?
A.
2
4.x
B.
2
2.yx
C.
2
1.
4
yx
D.
2
1.
2
yx
Lời giải
Chọn B.
Giả sử hàm số có dạng:
2.y ax
Theo giả thiết, đồ thị đi qua điểm
1;2
nên:
2
2 .1 2.aa
Vậy hàm số có dạng
2
2.yx