Câu 1 (1,0 đim). Tm điu kin đ biu thc sau c ngha
2
23 2
xx

.
Câu 2 (1,0 đim). Không s dng my tnh gii phương trnh sau:
22( 3 1) 2 3 3 0xx
.
Câu 3 (1,0 đim). Cho hàm số
2
y (3 2m)x
với
3
2
m
. Tm m đ hàm số nghịch biến
khi
0x
.
Câu 4 (1,0 đim). Cho (P)
2
yx
và đường thẳng (d)
2y x m
. Xc định m đ
đường thẳng (d) cắt parabol (P) tại hai đim phân bit A và B, biết một đim c hoành
độ
. Tm hoành độ đim còn lại.
Câu 5 (1,0 đim). Rút gọn biu thc A=
3x 9x 3 1 1 1
:x1
x x 2 x 1 x 2






, biết
0 x,x 1
.
Câu 6 (1,0 đim). Một ô tô dự định đi từ A và đến B lúc 12 giờ trưa. Nếu xe đi với vận
tốc 35km/h th đến B chậm 2h so với dự định. Nếu xe đi với vận tốc 50km/h th đến B
sớm hơn 1h so với dự định. Tnh quãng đường AB và thời đim xe xuất pht từ A.
Câu 7 (1,0 đim). Cho tam gic ABC vuông tại A, đường cao AH. Biết
AC 5
AB 3
,
30AH cm
. Tnh HB, HC?
Câu 8 (1,0 đim). Cho hnh vuông ABCD c cạnh là 2 cm. Đường tròn tâm O ngoại
tiếp hnh vuông. Tnh din tch hnh tròn tâm O?
Câu 9 (1,0 đim). Cho hai đường tròn (O) và (O’) cắt nhau tại A và B. Qua A vẽ hai ct
tuyến CAD và EAF (C,E (O); D,F (O’)). Đường thẳng CE cắt đường thẳng DF tại
P. Chng minh t gic BEPF nội tiếp.
Câu 10 (1,0 đim). Cho tam gic ABC nhọn nội tiếp đường tròn (O), gọi BD, CE là
cc đường cao của tam gic ABC. Chng minh OA DE.
........... Hết ............
Cn b coi thi không phi gii thch g thêm !
Họ và tên thí sinh:..................................................................... Số báo danh:.............................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO THÁI NGUYÊN
TRƯỜNG THPT NGÔ QUYỀN
ĐỀ THI THỬ TUYỂN SINH VÀO LỚP 10 THPT
NĂM HC 2022
-
2023
MÔN THI: TOÁN HC
Thời gian làm bài:120 phút (không kể thời gian phát đề)
SỞ
GIÁO DỤC VÀ ĐÀO TẠO THÁI NGUYÊN
TRƯỜNG THPT NGÔ QUYỀN
ĐP
N ĐỀ
THI TH
TUYỂN SINH VÀO LỚP
10
THPT
-
MÔN TON
NĂM HỌC 2022-2023
Câu 1
ĐK
2 3 0
20
x
x


3
2
2
x
x
0,5đ
0,5đ
Câu 2.
Ta c
1; 2( 3 1); 2 3 3a b c
V a+b+c= 0 nên phương trnh c nghim
12
1; 2 3 3
c
xx
a
0,25đ
0,25 đ
0,5đ
Câu 3.
Hs nghch bin khi x < 0 th a > 0
3-2m > 0
3
2
m
Vy
3
2
m
th hm s nghch bin khi x < 0
0,25đ
0,5
0,25 đ
Câu 4. Xt pt: x2 = 2x+m
220x x m
V phương trnh c nghim x = -1 nên ta c (-1)2 – 2.(-1) – m = 0
3 0 3mm
Vi m = 3 ta c pt x2 -2x - 3=0 , s dng HQ Vi-t ta c
12
1; 3xx
Vi x1 = -1 thay vo HS y = x2 ta đưc y1 = 1, do đ A(-1;1)
Vi x2 = 3 thay vo HS y = x2 ta đưc y2 = 9, do đ B(3;9)
0,25đ
0,25đ
0,25đ
0,25đ
Câu 5.
3x 9x 3 1 1 1
:x1
x x 2 x 1 x 2






=
3 3 2 1 1
( ): 1
( 1)( 2)
x x x x
x
xx

0,25đ
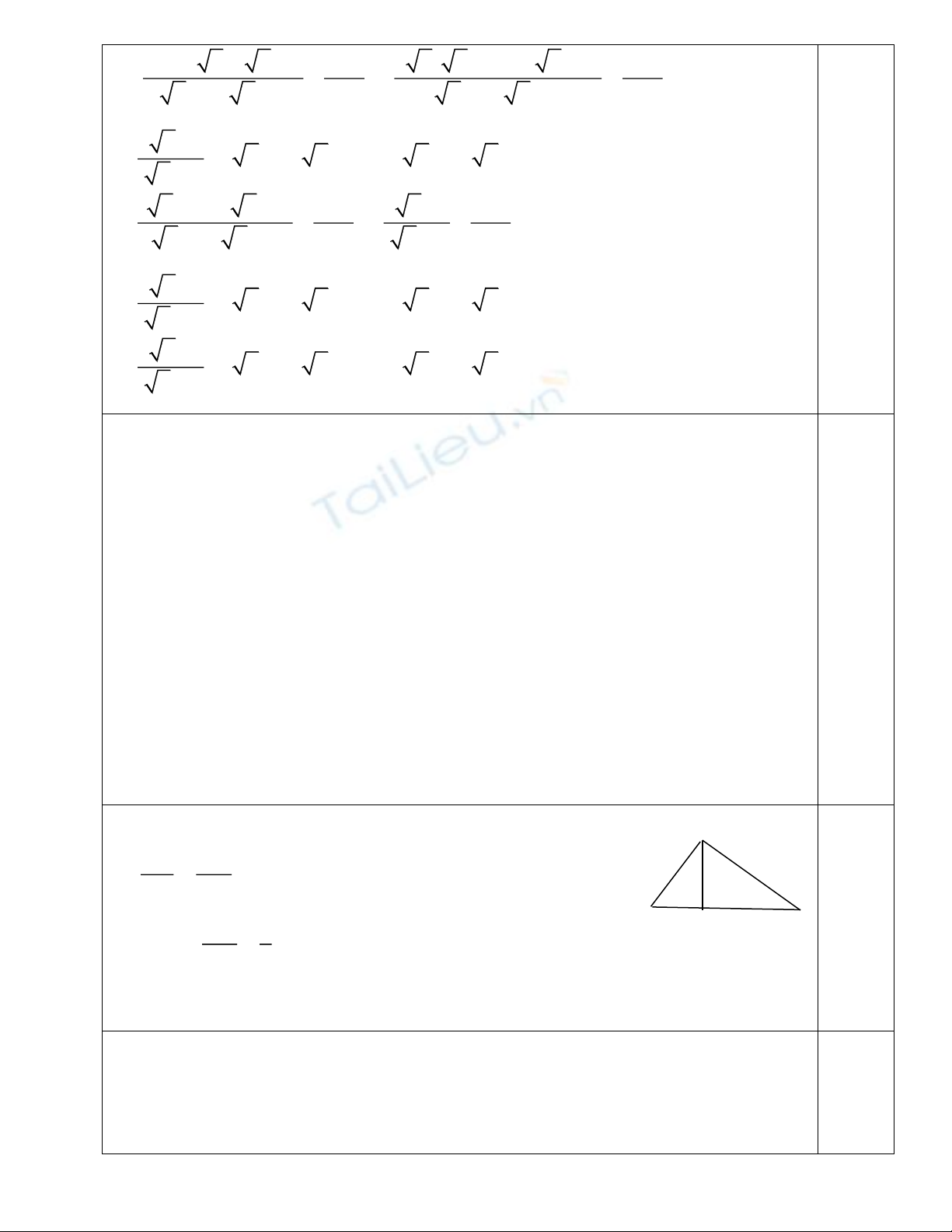
3 6 2 1 3 ( 2) ( 2) 1
( ): ( ):
11
( 1)( 2) ( 1)( 2)
x x x x x x
xx
x x x x


31
( ):( 1)( 1) (3 1)( 1)
1
xx x x x
x
( 2)(3 1) 1 3 1 1
( ): ( ):
11
( 1)( 2) 1
x x x
xx
x x x


31
( ):( 1)( 1) (3 1)( 1)
1
xx x x x
x
31
( ):( 1)( 1) (3 1)( 1)
1
xx x x x
x
0,25đ
0,25đ
0,25đ
Câu 6. Gọi độ di quãng đường AB l x (km; x> 0) v thời gian dự đnh l y (h;
y > 1)
Thời gian xe chạy ht quãng đường vi vn tc 30 km/h l y + 2 ( giờ)
Theo bi ra ta c phương trnh:
x = 35 ( y + 2)
Thời gian xe chạy ht quãng đường vi vn tc 50 km/h l y - 1 ( giờ)
Theo bi ra ta c phương trnh:
x = 50 ( y - 1)
Do đ ta c h phương trnh
)(
)(
150
235
yx
yx
5050
7035
yx
yx
350
8
x
y
(TMĐK)
Vy quãng đường ô AB l 350 km v thời điểm xuất phát của ô tô tại A l
12 - 8 = 4 ( giờ sáng)
0,25
0,5
0,25
Câu 7. V hnh
V
AC AH
AB BH
Nên ta c
30 5
3BH
, do đ BH = 18 cm
M
2.AH BH CH
nên ta c CH= 50 cm
0,25đ
0,25đ
0,25đ
0,25đ
Câu 8. (Không c điểm v hnh)
Tâm O của đường trn ngoại tip hnh vuông l trung điểm của đoạn AC, bán
knh của đường trn l R= OA=OC=OB
0,25đ
A
C
H
B
Ch : Hc sinh lm theo cch khc m đng th vn cho đim ti đa
2 2 2 2
2 2 2 2AC AB BC cm
2
2
AC
R cm
Vy din tch hnh trn cn tm l
2 2 2
( 2) 2S R cm
0,25đ
0,25đ
0,25đ
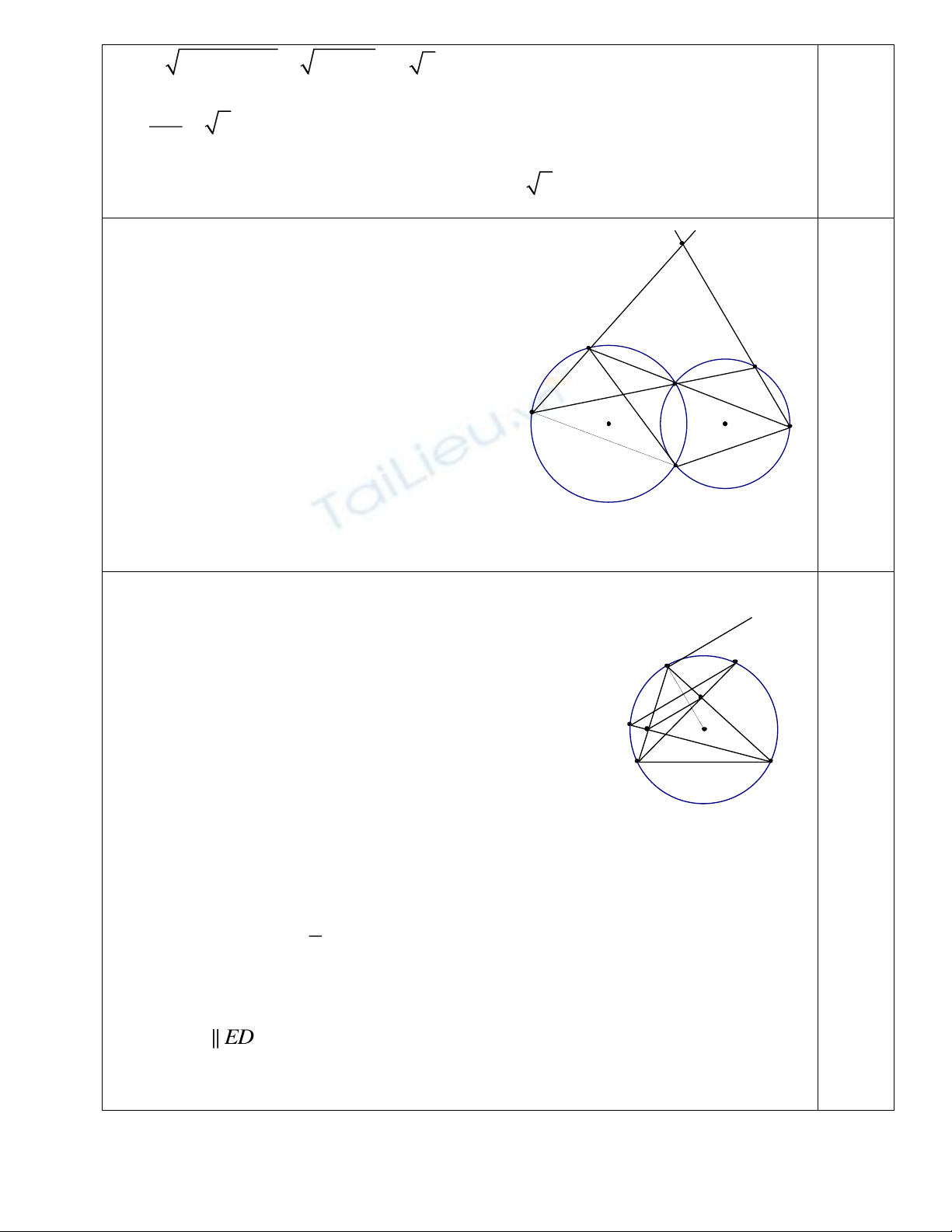
Câu 9. V hnh
Ta c
BEP ECB EBC
(gc ngoi BCE)
m
ECB BAF
(gc ngoi của tứ giác ABCE
nội tip)
EBC EAC DAF
nên
BEP BAF DAF BAD
M tứ giác ABFD nội tip nên
0
180BAD BFD
0
180BEP BFP
BEPF l tứ giác nội
tip.
0,25đ
0,25đ
0,25đ
0,25đ
Câu 10. V hnh
Gọi M,N ln lưt l giao điểm của đường thng BD,
CE vi đường trong tâm O
Ta c
ACN ABM AM AN
(gc c cp cạnh tương
ứng vuông gc)
Do đ A l điểm chnh giữa của cung MN
OA MN (1)
Tứ giác BEDC nội tip v
0
90BEC BDC
Suy ra
1d
2
DEC DBC s DC
M
DBC MNC
( Hai gc nội tip cng chn cung MC)
Do đ
MN ED
(2)
T (1) v (2) OA DE
0,25đ
0,25đ
0,25đ
0,25đ
B
A
P
O
O'
E
F
C
D
x
D
E
O
A
B
C
M
N