WWW.VNMATH.COM
Đ s 34ề ố
Đ THI TH H C KÌ 2 – Năm h c 2010 – 2011Ề Ử Ọ ọ
Môn TOÁN L p 11ớ
Th i gian làm bài 90 phútờ
I. Ph n chung:ầ (7,0 đi m)ể
Câu 1: (2,0 đi m) Tìm các gi i h n sau:ể ớ ạ
a)
n n
n n
3 4 1
lim 2.4 2
− +
÷
÷
+
b)
( )
x
x x x
2
lim
→+∞ − −
Câu 2: (1,0 đi m) Xét tính liên t c c a hàm s sau t i đi m ể ụ ủ ố ạ ể x = 3:
xkhi x
x
f x
khi x
x
2
33
9
( ) 13
12
−<
−
=
≥
Câu 3: (1,0 đi m) Tính đ o hàm c a các hàm s sau:ể ạ ủ ố
a)
x x
yx
2
2 6 5
2 4
− +
=+
b)
x x
yx x
sin cos
sin cos
+
=−
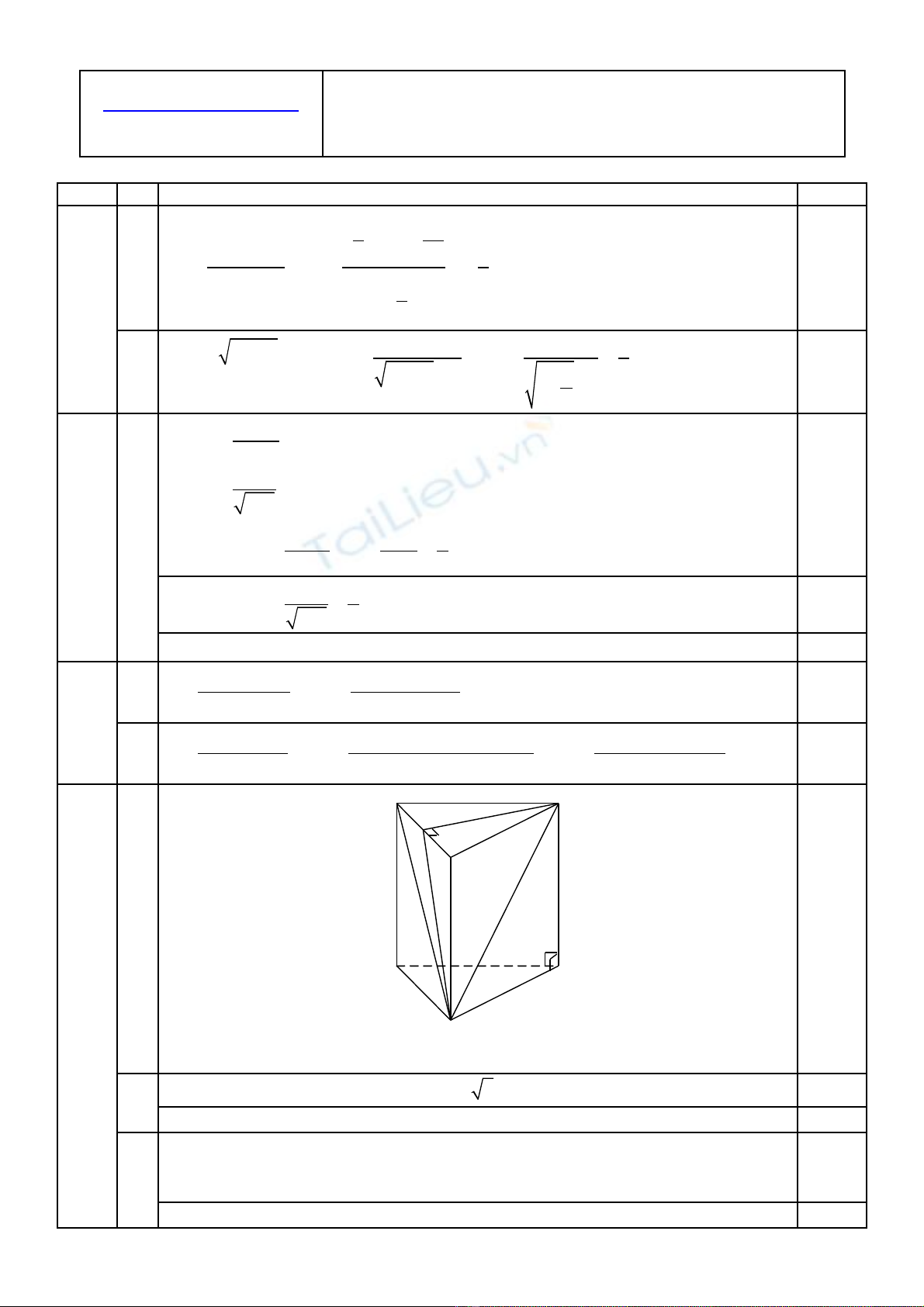
Câu 4: (3,0 đi m) Cho hình lăng tr đ ng ABC.Aể ụ ứ ′B′C′ có AB = BC = a, AC =
a2
.
a) Ch ng minh r ng: BC ứ ằ ⊥ AB′.
b) G i M là trung đi m c a AC. Ch ng minh (BCọ ể ủ ứ ′M) ⊥ (ACC′A′).
c) Tính kho ng cách gi a BBả ữ ′ và AC′.
II. Ph n riêng:ầ (3,0 đi m) ểThí sinh ch đ c ch n m t trong hai ph n sau:ỉ ượ ọ ộ ầ
1. Theo ch ng trình Chu nươ ẩ
Câu 5a: (1,0 đi m) Tính gi i h n:ể ớ ạ
n
n n
2
1 2 ...
lim 3
+ + +
+
.
Câu 6a: (2,0 đi m) ể
a) Cho hàm s ố
. Ch ng minh: ứ
y y 0
′′+ =
.
b) Vi t ph ng trình ti p tuy n c a đ th hàm s ế ươ ế ế ủ ồ ị ố
y x x
3 2
3 2= − +
t i đi m M ( –1; –2).ạ ể
2. Theo ch ng trình Nâng caoươ
Câu 5b: (1,0 đi m) Tìm ểx đ ba s ể ố a, b, c l p thành m t c p s c ng, v i: ậ ộ ấ ố ộ ớ
a x10 3= −
,
b x2
2 3= +
,
c x7 4
= −
.
Câu 6b: (2,0 đi m)ể
a) Cho hàm s : ố
x x
y
22 2
2
+ +
=
. Ch ng minh r ng: ứ ằ
y y y 2
2 . 1
′′ ′
− =
.
b) Vi t ph ng trình ti p tuy n c a đ th hàm s ế ươ ế ế ủ ồ ị ố
y x x
3 2
3 2= − +
, bi t ti p tuy n vuông góc v iế ế ế ớ
đ ng th ng d: ườ ẳ
y x
12
9
= − +
.
--------------------H t-------------------ế
H và tên thí sinhọ: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . SBD :. . . . . . . . . .
1
WWW.VNMATH.COM
Đ s 34ề ố
ĐÁP ÁN Đ THI TH H C KÌ 2 – Năm h c 2010 – 2011Ề Ử Ọ ọ
Môn TOÁN L p 11ớ
Th i gian làm bài 90 phútờ
Câu Ý N i dungộĐi mể
1a)
3 1
1
4
3 4 1 1
4
lim lim 2
2.4 2 1
22
n
n n n
n n n
− +
÷
− +
= = −
÷
÷
+
+ ÷
1,00
b)
( )
2
2
1 1
lim lim lim 2
1
1 1
x x x
x
x x x
x x x
x
→+∞ →+∞ →+∞
− −
− − = = =
− + − +
1,00
2
xkhi x
x
f x
khi x
x
2
33
9
( ) 13
12
−<
−
=
≥
x x x
x
f x x
x
2
3 3 3
3 1 1
lim ( ) lim lim 3 6
9
− − −
→ → →
−
= = =
+
−
0,25
x x
f x f
x
3 3
1 1
lim ( ) lim (3)
6
12
+ +
→ →
= = =
0,50
⇒
f x( )
liên t c t i ụ ạ x = 3 0,25
3a)
x x x x
y y
xx
2 2
2
2 6 5 4 16 34
'
2 4 (2 4)
− + + −
= ⇒ =
++
1,00
b)
x x x x x x x
y y y
x x x x x x
2
2 2
sin cos (cos sin ) cos2 sin2 cos2 1
' '
sin cos (sin cos ) (sin cos )
+ − − − − −
= ⇒ = ⇒ =
−− −
1,00
4
A B
C
A’
C’
B’
M
0,25
a) Tam giác ABC có
2 2 2 2 2
2 ( 2)AB BC a a AC+ = = = ⇒
∆ABC vuông t i Bạ0,25
, '( ) (AA ' ' ) 'BC AB BC BB gt BC B B BC AB⇒ ⊥ ⊥ ⇒ ⊥ ⇒ ⊥
0,50
b) G i M là trung đi m c a AC. Ch ng minh (BCọ ể ủ ứ ′M) ⊥ (ACC′A′).
*) Tam giác ABC cân t i B, MA = MC ạ
, '( ' ( )) (AA ' ' )BM AC BM CC CC ABC BM C C⇒ ⊥ ⊥ ⊥ ⇒ ⊥
0,50
( ' ) ( ' ) ( ' ')BM BC M BC M ACC A⊂ ⇒ ⊥
0,50
2
c) Tính kho ng cách gi a BBả ữ ′ và AC′.
BB′ // (AA′C′C) ⇒
d BB AC d BB AA C C d B AA C C( , ) ( ,( )) ( ,( ))
′ ′ ′ ′ ′ ′ ′
= =
0,50
AC a
BM AA C C d B AA C C BM 2
( ) ( ,( )) 2 2
′ ′ ′ ′
⊥ ⇒ = = =
0,50
5a Tính gi i h n:ớ ạ
2
1 2 ...
lim 3
n
I
n n
+ + +
=+
.
Vi t l i ế ạ
n n n n
n n n
n n
2
1 2 3 ... ( 1) 1
2 ( 3) 2( 3)
3
+ + + + + +
= =
+ +
+
0,50
nn
In
n
1
1
1 1
lim lim 6
2 6 2
2
+
+
= = =
++
0,50
6a a) Cho hàm s ố
. Ch ng minh: ứ
y y 0
′′+ =
.
y x x2010sin 2011cos
′= − +
,
" 2010cos 2011siny x x= − −
0,50
" 2010cos 2011sin 2010cos 2011sin 0y y x x x x+ = − − + + =
0,50
b) Vi t PTTT c a đ th hàm s ế ủ ồ ị ố
y x x
3 2
3 2= − +
t i đi m M ( –1; –2).ạ ể
y x x k y
2
3 6 ( 1) 9
′ ′
= − ⇒ = − =
0,50
Ph ng trình ti p tuy n là ươ ế ế
y x9 7= +
0,50
5b Tìm x đ ba s ể ố a, b, c l p thành CSC, v i: ậ ớ
a x10 3
= −
,
b x2
2 3= +
,
c x7 4
= −
.
Có
a c b x x
2
2 17 7 4 6+ = ⇔ − = +
0,50
x
x x x
2
1
4 7 11 0 11
4
=
⇔ + − = ⇔ −
=
0,50
6b a) Cho hàm s : ố
x x
y
22 2
2
+ +
=
. Ch ng minh r ng: ứ ằ
y y y 2
2 . 1
′′ ′
− =
.
y x y' 1 " 1= + ⇒ =
0,50
y y x x x x x y
2 2 2 2
2 . " 1 ( 2 2).1 1 2 1 ( 1) ′
− = + + − = + + = + =
0,50
b) Vi t ếPTTT c a đ th hàm s ủ ồ ị ố
y x x
3 2
3 2= − +
, bi t TT vuông góc v i đ ngế ớ ườ
th ng d: ẳ
y x
12
9
= − +
.
*) Vì TT vuông góc v i d: ớ
y x
12
9
= − +
nên h s góc c a TT là ệ ố ủ k = 9
0,25
G i ọ
x y
0 0
( ; )
là to đ c a ti p đi m.ạ ộ ủ ế ể
y x k x x x x
2
0 0 0 0 0
( ) 3 6 9 0 1, 3
′= ⇔ − − = ⇔ = − =
0,25
V i ớ
x y PTTT y x
0 0
1 2 : 9 7= − ⇒ = − ⇒ = +
0,25
x y PTTT y x
0 0
3 2 : 9 25= ⇒ = ⇒ = −
0,25
3