CH NG I. ĐI N TÍCH . ĐI N TR NGƯƠ Ệ Ệ ƯỜ
ĐNH LU T CULOMBỊ Ậ
A. LÝ THUY TẾ
1. Hai lo i đi n tích: ạ ệ
- Đi n tích d ng và đi n tích âmệ ươ ệ
- Đi n tích d ng nh nh t là c a proton, đi n tích âm nh nh t là đi n tích c a electron. Giá tr tuy t đi c a chúng là e =ệ ươ ỏ ấ ủ ệ ỏ ấ ệ ủ ị ệ ố ủ
1,6.10-19C
2. T ng tác gi a hai đi n tích đi m đng yên.ươ ữ ệ ể ứ
- Đi m đt: T i đi n tích đang xét.ể ặ ạ ệ
- Giá: Là đng th ng n i hai đi n tích.ườ ẳ ố ệ
- Chi u: là l c đyn u hai đi n tích cùng d u, l c hút n u hai đi n tích trái d u.ề ự ẩ ế ệ ấ ự ế ệ ấ
- Đ l n: ộ ớ
1 2
2
q q
F k r
=ε
Trong đó k = 9.109
( )
2 2
Nm / c
.
ε
: là h ng s đi n môi.ằ ố ệ
3. Đnh lu t b o toàn đi n tích:ị ậ ả ệ
Trong m t h cô l p v đi n, t ng đi s các đi n tích là m t h ng sộ ệ ậ ề ệ ổ ạ ố ệ ộ ằ ố
4. Khi đi n tích ch u tác d ng c a nhi u l c:ệ ị ụ ủ ề ự
H p l c tác d ng lên đi n tích Là: ợ ự ụ ệ
1 2 n
F F F ... F= + + +
r r r r
(1)
a. Ph ng pháp chi u:ươ ế
- Ch n h tr c t a đ Oxy phù h p v i đi u ki n c a bài toán.ọ ệ ụ ọ ộ ợ ớ ề ệ ủ
- Chi u (1) lên Ox, Oy:ế
x 1x 2x nx 2 2
x y
y 1y 2 y ny
F F F ... F F F F
F F F ... F
= + + +
= +�
= + + +
F
r
h p v i tr c Ox m t góc : αợ ớ ụ ộ
y
x
F
tan F
α =
b. Ph ng pháp hình h c:ươ ọ
Xét tr ng h p ch có hai l c:ườ ợ ỉ ự
1 2
F F F= +
r r r
a. Khí
1
F
r
cùng h ng v i ướ ớ
: F = F1 + F2;
F
r
cùng h ng v i ướ ớ
1
F
r
,
:
b. Khi
1
F
r
ng c h ng v i ượ ướ ớ
:
1 2
F F F= −
;
F
r
cùng h ng v i ướ ớ
11 2
21 2
F khi : F F
F khi : F F
>
<
r
r
c. Khi
1 2
F F⊥
r r
:
2 2
1 2
F F F= +
;
F
r
h p v i ợ ớ
1
F
r
m t góc ộ
α
xác đnh b i:ị ở
2
1
F
tan F
α =
d. Khi F1 = F2 và
ﾷ
12
F , F = α
r
:
1
F 2F cos 2
α
� �
=� �
� �
;
F
r
h p v i ợ ớ
1
F
r
m t góc ộ
2
α
e. T ng quát: khi ổ
1
F
r
h p v i ợ ớ
m t góc :αộ
2 2
1 2 1 2
F F F 2F F cos= + + α
1
B. BÀI T P VÍ D :Ậ Ụ
Bài 1: Hai đi n tích đi m cách nhau m t kho ng r =3m trong chân không hút nhau b ng m t l c F=6.10ệ ể ộ ả ằ ộ ự -9N. Đi n tích t ng c ngệ ổ ộ
c a hai đi n tích đi m là Q=10ủ ệ ể -9C. Tính đi n đích c a m i đi n tích đi m.ệ ủ ỗ ệ ể
H ng d n gi i:ướ ẫ ả
Áp d ng đnh lu t Culong: ụ ị ậ
1 2
2
q q
F k r
=ε
( )
2
18 2
1 2
Fr
q q 6.10 C
k
−
ε
= =�
(1)
Theo đ: ề
9
1 2
q q 10 C
−
+ =
(2)
Gi h (1) và (2) ả ệ
9
1
9
2
q 3.10 C
q 2.10 C
−
−
=
= −
Bài 2: Hai qu c u gi ng nhau mang đi n, cùng đt trong chân không, và cách nhau kho ng r = 1m thì chúng hút nhau m t l cả ầ ố ệ ặ ả ộ ự
F1=7,2N. Sau đó cho hai qu c u đó ti p xúc v i nhau và đa tr l i v trí cũ thì chúng đy nhau m t l c Fả ầ ế ớ ư ở ạ ị ả ộ ự 2=0,9N. tính đi n tích m iệ ỗ
qu c u tr c và sau khi ti p xúc.ả ầ ướ ế
H ng d n gi i:ướ ẫ ả
Tr c khi ti p xúc ướ ế
( )
2
10 2
1 2
Fr
q q 8.10 C
k
−
ε
= = −�
(1)
Đi n tích hai qu c u sau khi ti p xúc:ệ ả ầ ế
, , 1 2
1 2
q q
q q 2
+
= =
2
1 2
5
2 1 2
2
q q
2
F k q q 2.10 C
r
−
+
� �
� �
� �
= + =� �
ε
(2)
T h (1) và (2) suy ra: ừ ệ
5
1
5
2
q 4.10 C
q 2.10 C
−
−
=
=
m
Bài 3: Hai đi n tích qệ1, q2 đt cách nhau m t kho n r=10cm thì t ng tác v i nhau b ng l c F trong không khí và b ng ặ ộ ả ươ ớ ằ ự ằ
F
4
n u đtế ặ
trong d u. Đ l c t ng tác v n là F thì hai đi n tích ph i đt cách nhau bao nhiêu trong d u?ầ ể ự ươ ẫ ệ ả ạ ầ
H ng d n gi i:ướ ẫ ả
1 2 1 2 ,
2 ,2
q q q q r
F k k r 5cm
r r
= = = =�
εε
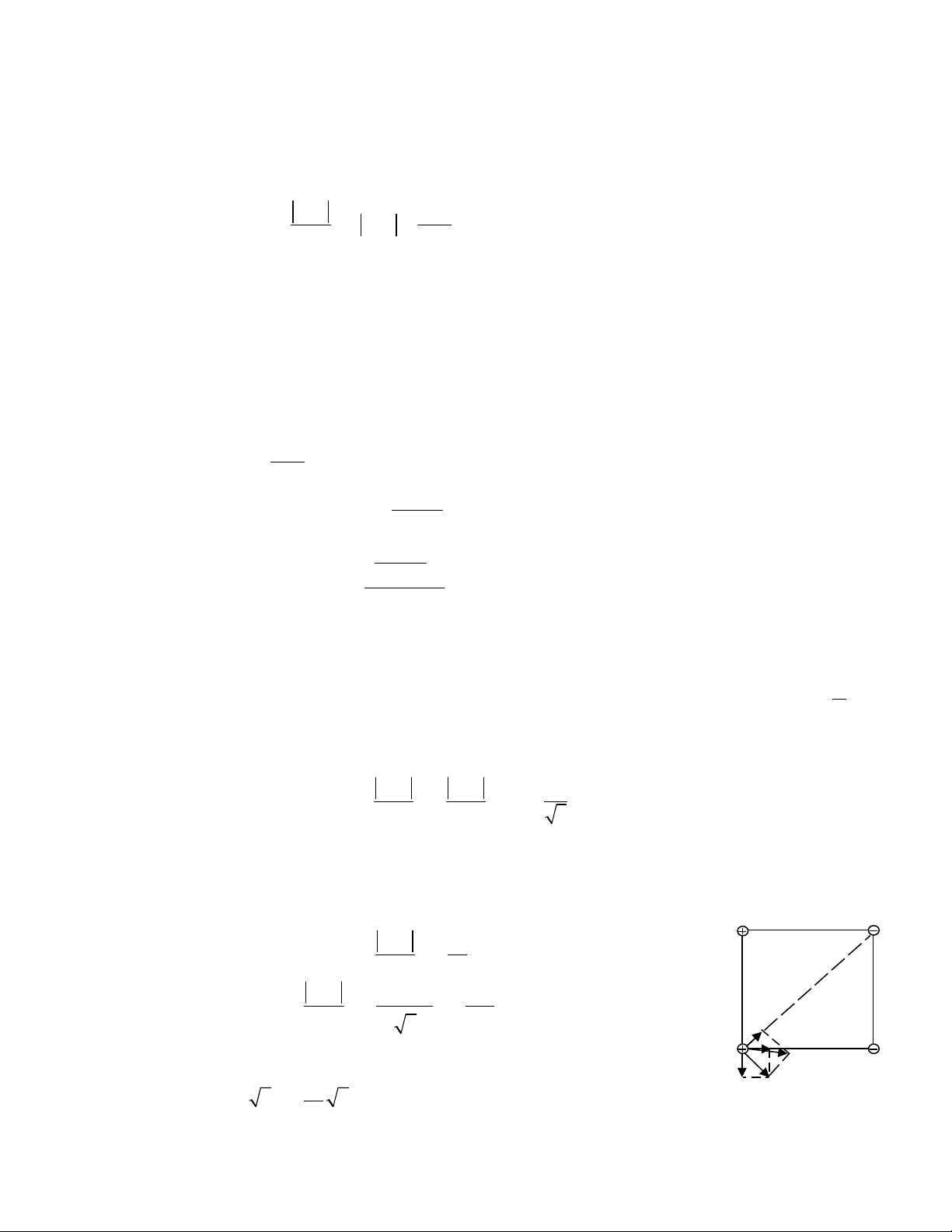
Bài 4: Cho hai đi n tích b ng +q (q>0) và hai đi n tích b ng –q đt t i b n đnh c a m t hình vuông ABCD c nh a trong chânệ ằ ệ ằ ặ ạ ố ỉ ủ ộ ạ
không, nh hình v . Xác đnh l c đi n t ng h p tác d ng lên m i đi n tích nói trênư ẽ ị ự ệ ổ ợ ụ ỗ ệ
H ng d n gi i:ướ ẫ ả
Các l tác d ng lên +q D nh hình v , ta cóự ụ ở ư ẽ
2
1 2
AD CD 2 2
q q q
F F k k
r a
= = =
( )
2 2
1 2
BD 2
2 2
q q q q
F k k k
r 2a
a 2
= = =
D AD CD BD 1 BD
F F F F F F= + + = +
r r r r r r
2
1 AD 2
q
F F 2 k 2
a
= =
;
1
F
r
h p v i CD m t góc 45ợ ớ ộ 0.
2
FBD
FCD
A B
C
D
2
2 2
D 1 BD 2
q
F F F 3k 2a
= + =
Đây cũng là đ l n l c tác d ng lên các đi n tích khácộ ớ ự ụ ệ
Bài 5: Cho hai đi n tích qệ1=
4 Cµ
, q2=9
Cµ
đt t i hai đi m A và B trong chân không AB=1m. Xác đnh v trí c a đi m M đ đtặ ạ ể ị ị ủ ể ể ặ
t i M m t đi n tích qạ ộ ệ 0, l c đi n t ng h p tác d ng lên qự ệ ổ ợ ụ 0 b ng 0, ch ng t r ng v trí c a M không ph thu c giá tr c a qằ ứ ỏ ằ ị ủ ụ ộ ị ủ 0.
H ng d n gi i:ướ ẫ ả
Gi s qả ử 0 > 0. H p l c tác d ng lên qợ ự ụ 0:
10 20
F F 0+ =
r r r
Do đó:
1 0 1 0
10 20 2
q q q q
F F k k AM 0, 4m
AM AB AM
= = =� �
−
Theo phép tính toán trên ta th y AM không ph thu c vào qấ ụ ộ 0.
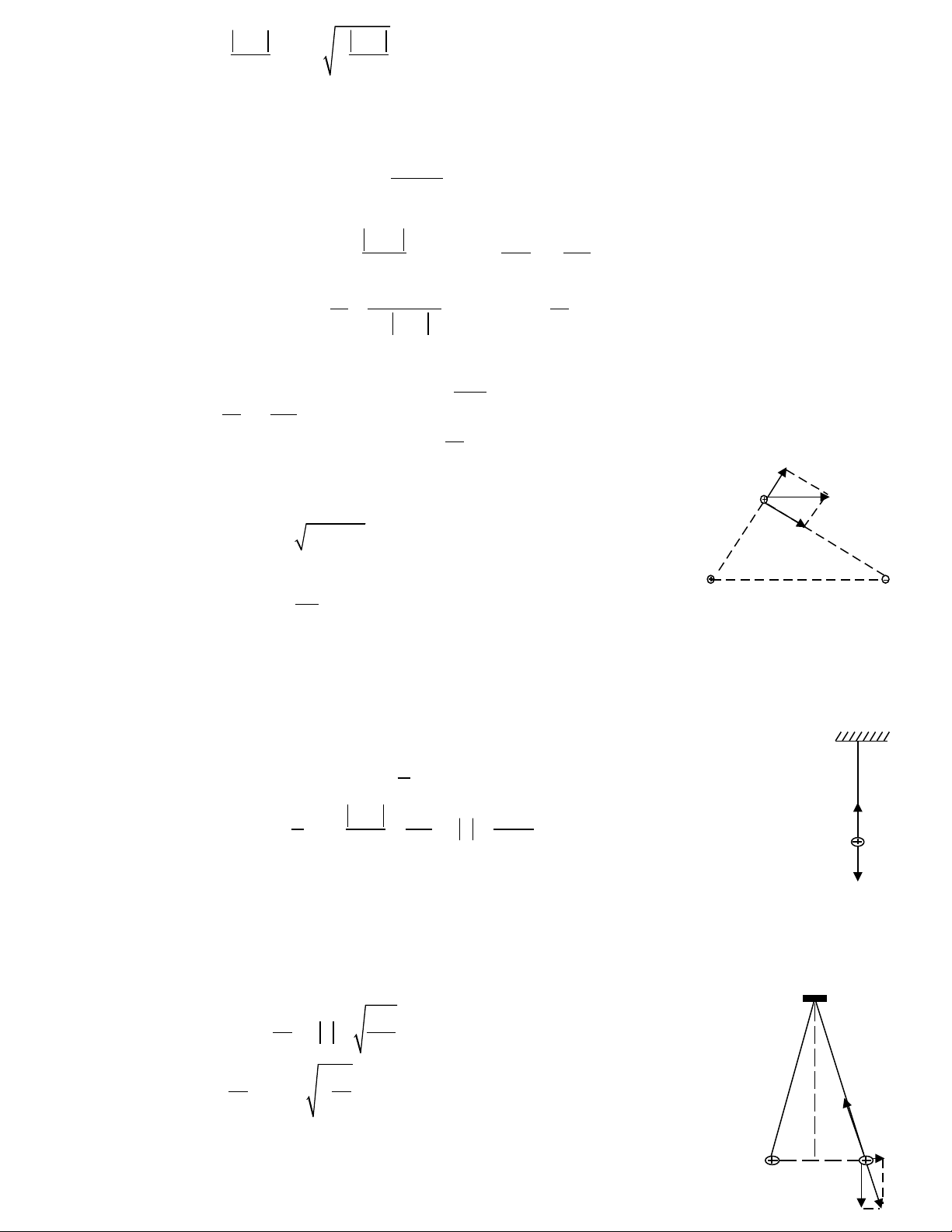
Bài 6: Cho hai đi n tích đi m qệ ể 1=16
Cµ
và q2 = -64
Cµ
l n l t đt t i hai đi m A và B trong chân không cách nhau AB = 100cm.ầ ượ ặ ạ ể
Xác đnh l c đi n t ng h p tác d ng lên đi n tích đi m qị ự ệ ổ ợ ụ ệ ể 0=4
Cµ
đt t i:ặ ạ
a. Đi m M: AM = 60cm, BM = 40cm.ể
b. Đi m N: AN = 60cm, BN = 80cmể
H ng d n gi i:ướ ẫ ả
a. Vì MA + MB = AB v y 3 đi m M, A, B th ng hàng M n m gi a AB. ậ ể ẳ ằ ữ L c đi n t ng h p tác d ng lên qự ệ ổ ợ ụ 0:
10 20
F F F= +
r r r
Vì
10
F
r
cùng h ng v i ườ ớ
20
F
r
nên:
1 0 2 0
10 20 2 2
q q q q
F F F k k 16N
AM BM
= + = + =
F
r
cùng h ng v i ườ ớ
10
F
r
và
20
F
r
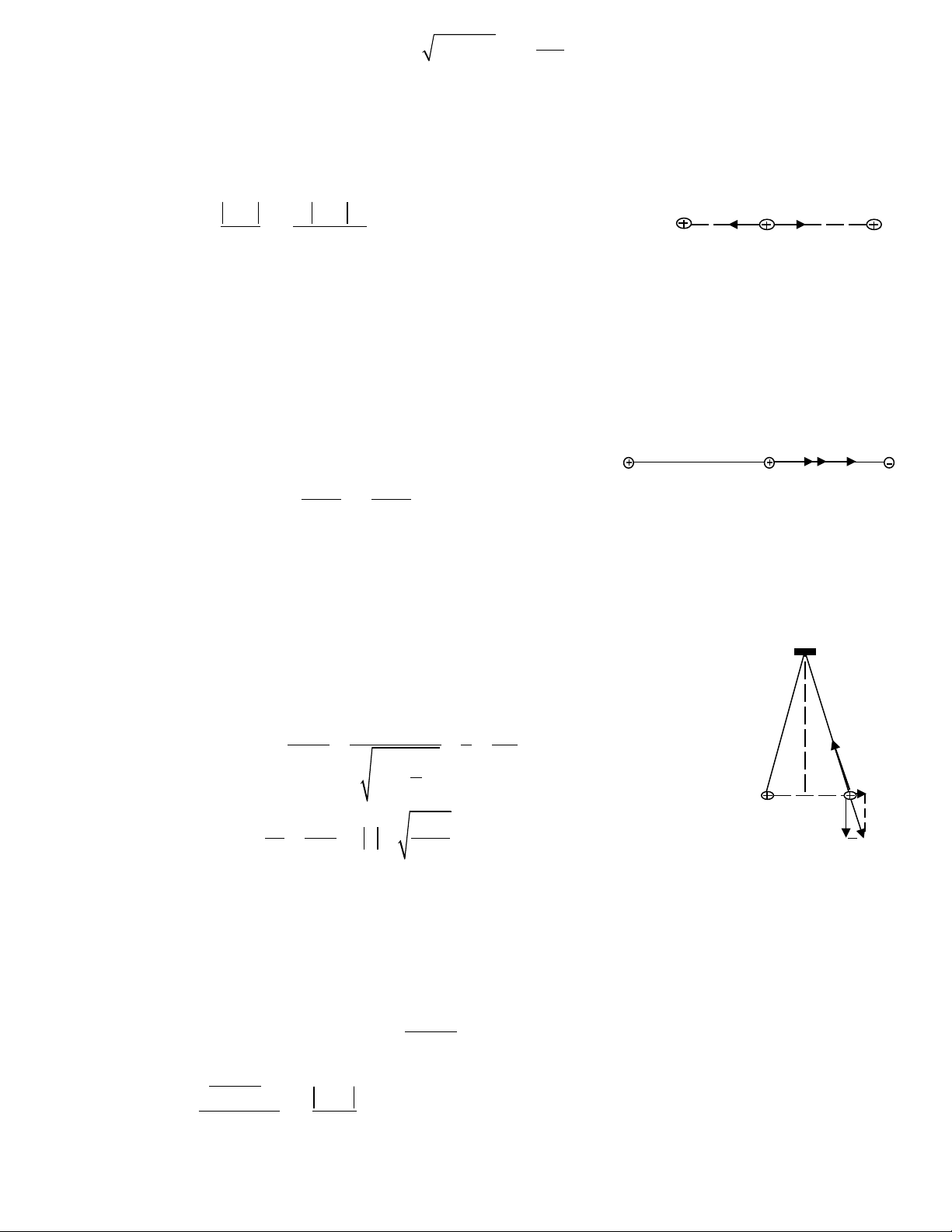
Bài 7: Ng i ta treo hai qu c u nh có kh i l ng b ng nhau m = 0,01g b ng nh ng s i dây có chi u dài b ng nhau (kh i l ngườ ả ầ ỏ ố ượ ằ ằ ữ ợ ề ằ ố ượ
không đáng k ). Khi hai qu c u nhi m đi n b ng nhau v đ l n và cùng d u chúng đy nhau và cách nhau m t kho ng r=6cm.ể ả ầ ễ ệ ằ ề ộ ớ ấ ẩ ộ ả
L y g=9,8m/sấ2. Tính đi n tích m i qu c uệ ỗ ả ầ
H ng d n gi iướ ẫ ả :
Ta có:
P F T 0+ + =
ur r ur r
T hình v :ừ ẽ
2
2
2 3
9
2
r r r F
tan 2.OH 2 mg
r
2 l 2
q rmg r mg
k q 1,533.10 C
r 2l 2kl
−
α = = =
��
−��
��
= = =� �
Bài 8: Hai qu c u kim lo i nh hoàn toàn gi ng nhau mang đi n tích qả ầ ạ ỏ ố ệ 1=1,3.10-9C và q2 = 6.5.10-9C, đt trong không khí cách nhauặ
m t kho ng r thì đy nhau v i l c F. Cho hai qu c u ti p xúc nhau, r i đt chúng trong m t l p đi n môi l ng, cũng cách nhauộ ả ẩ ớ ự ả ầ ế ồ ặ ộ ớ ệ ỏ
m t kho ng r thì l c đy gi a chúng cũng b ng Fộ ả ự ẩ ữ ằ
a. Xác đinh h ng s đi n môi ằ ố ệ
ε
b. Bi t l c tác d ng F = 4,6.10ế ự ụ -6N. Tính r.
H ng d n gi i:ướ ẫ ả
a. Khi cho hai qu c u ti p xúc nhau thì: ả ầ ế
, , 1 2
1 2
q q
q q 2
+
= =
Ta có:
2
1 2
1 2
,
2 2
q q
q .q
2
F F k k 1,8
r r
+
� �
� �
� �
= = ε =� �
ε
3
q1 q0 q2
A B
F20 F10
A M F10 F20 F B
q1 q0 q2
O
αl
T
F
P Q
H
r
b. Kho ng cách r: ả
1 2 1 2
2
q q q q
F k r k 0,13m
r F
= = =�
Bài 9: Hai qu c u kim lo i gi ng nhau, mang đi n tích qả ầ ạ ố ệ 1, q2 đt cách nhau 20cm thì hút nhau b i m t l c F ặ ợ ộ ự 1 = 5.10-7N. N i haiố
qu c u b ng m t dây d n, xong b dây d n đi thì hai qu c u đy nhau v i m t l c Fả ầ ằ ộ ẫ ỏ ẫ ả ầ ẩ ớ ộ ự 2 = 4.10-7 N. Tính q1, q2.
H ng d n gi i:ướ ẫ ả
Khi cho hai qu c u ti p xúc nhau thì: ả ầ ế
, , 1 2
1 2
q q
q q 2
+
= =
Áp d ng đnh lu t Culong:ụ ị ậ
2
1 2 16
1
1 1 2
2
q .q F r 0, 2
F k q .q .10
r k 9
−
= = − = −�
( )
2
1 2 8
2
1 2
1 1 2
q q
F 4
q q .10 C
F 4 q q 15
−
+
= + =� �
V y qậ1, q2 là nghi m c a ph ng trình:ệ ủ ươ
8
2 19
8
10 C
4 0, 2 3
q q .10 0 q
15 9 110 C
15
−
−
−
− = =� �
b. Vì
2 2 2
NA NB AB NAB+ = ∆�
vuông t i N. H p l c tác d ng lên qạ ợ ự ụ 0 là:
10 20
F F F= +
r r r
2 2
10 20
F F F 3,94V= + =
F
r
h p v i NB m t góc ợ ớ ộ
α
:
tan
0
10
20
F0, 44 24
F
α = = α =�
Bài 10: M t qu c u nh có kh i l ng m = 1,6g, tích đi n q = 2.10ộ ả ầ ỏ ố ượ ệ -7C đc treo b ng m tượ ằ ộ
s i dây t m nh có chi u dài l = 1m. phía trên nó t i đi m treo c a s i dây c n ph i đt m t đi n tích qợ ơ ả ề Ở ạ ể ủ ợ ầ ả ặ ộ ệ 2 nh th nào đ l cư ế ể ự
căng dây gi m đi m t n a.ả ộ ử
H ng d n gi i:ướ ẫ ả
L c căng c a s i dây khi ch a đt đi n tích: T = P = mgự ủ ợ ư ặ ệ
L c căng c a s i dây khi đt đi n tích: T = P – F = ự ủ ợ ặ ệ
P
2
2
1 2 7
2
1
q q
P mg mgr
F k q 4.10 C
2 r 2 2kq
−
= = = =� � �
V y qậ2 > 0 và có đ l n qộ ớ 2 = 4.10-7C
Bài 11: Hai đi n tích đi m b ng nhau đt trong chân không, cách nhau kho ng rệ ể ằ ặ ả 1=4cm. L c đy tĩnh đi n gi aự ẩ ệ ữ
chúng là F = -10-5N
a. Tính đ l n m i đi n tích.ộ ớ ỗ ệ
b. Tìm kho ng cách rả2 gi a chúng đ l c đy tĩnh đi n là Fữ ể ự ẩ ệ 2 = 2,5.10-6N.
H ng d n gi i:ướ ẫ ả
a. Đ l n m i đi n tích:ộ ớ ỗ ệ
2
2
9
1 1
12
1
F rq
F k q 1,3.10 C
r k
−
= = =�
Kho ng cách rả2:
2 2
2
2 2
2
2 2
q q
F k r k 8.10 m
r F
−
= = =�
4
O
α
l
T
H F
q q
P Q
T
P
F10
N
q F
F20
A B
q1 q2
Bài 12: Hai qu c u nh gi ng nhau, cùng kh i l ng m = 0,2kg, đc treo t i cùng m t đi m b ng hai s i t m nh dài l = 0,5m.ả ầ ỏ ố ố ượ ượ ạ ộ ể ằ ợ ơ ả
Khi m i qu c u tích đi n q nh nhau, chúng tách nhau ra m t kho ng a=5cm. Xác đinh q.ỗ ả ầ ệ ư ộ ả
H ng d n gi i:ướ ẫ ả
Qu c u ch u tác d ng c a ba l c nh hình v . Đi u ki n cân b ng: ả ầ ị ụ ủ ự ư ẽ ề ệ ằ
P F T 0+ + =
ur r ur r
2
2
a
F2
tan Pa
l4
α = =
−
2
2
2
2
qa
ka2
mg a
l4
=
−
9
2 2
amg
q a. 5,3.10 C
k 4l a
−
= =�−
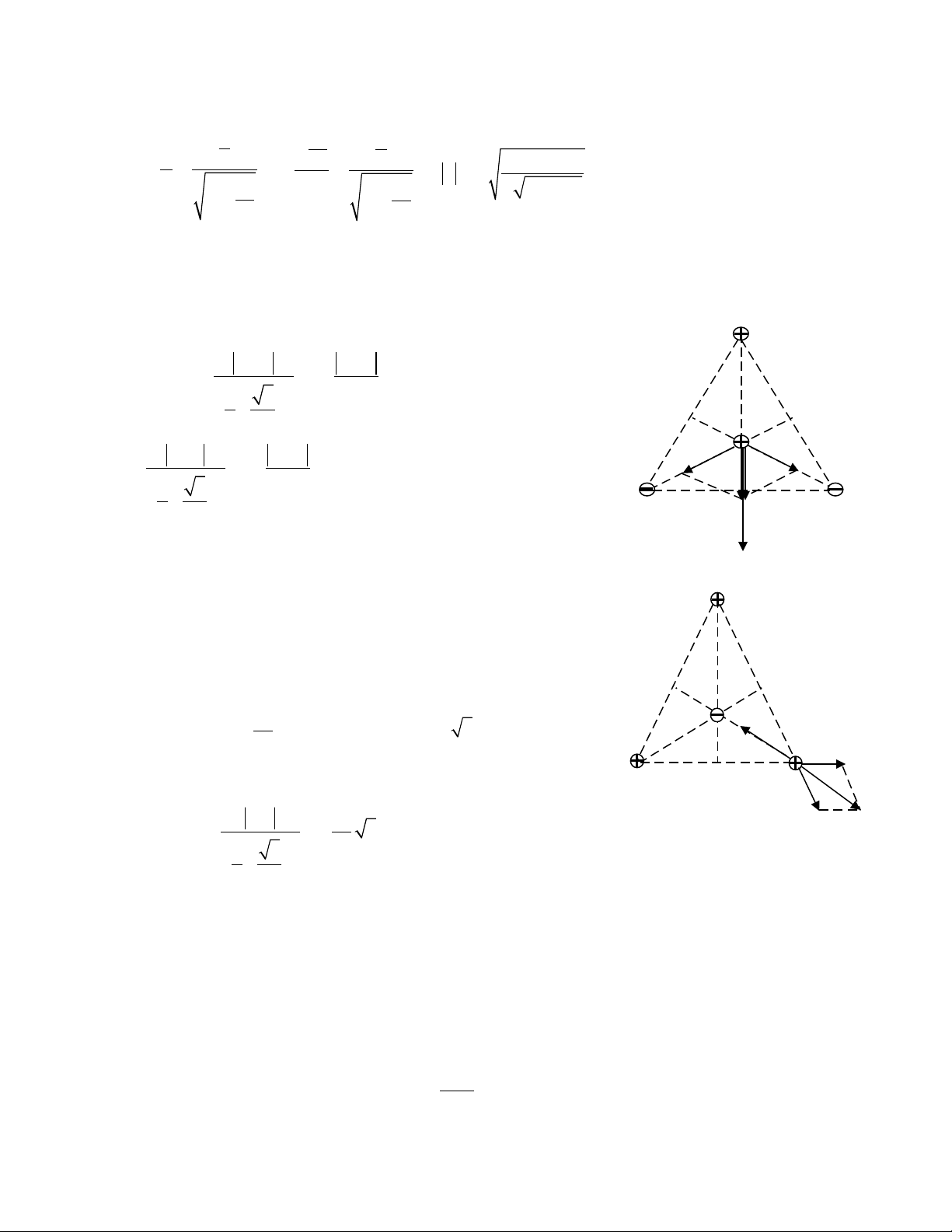
Bài 13: Ng i ta đt ba đi n tích qườ ặ ệ 1 = 8.10-9C, q2=q3=-8.10-C t i ba đnh c a m t tam giác đu ABC c nh a = 6cm trong khôngạ ỉ ủ ộ ề ạ
khí. Xác đnh l c tác d ng lên đi n tích qị ự ụ ệ 0= 6.10-9C đt t i tâm O c a tam giác.ặ ạ ủ
H ng d n gi i:ướ ẫ ả
L c t ng h p tác d ng lên qự ổ ợ ụ 0:
1 2 3 1 23
F F F F F F= + + = +
r r r r r r
1 0 1 0 5
122
q .q q .q
F k 3k 36.10 N
a
2 3
a
3 2
−
= = =
� �
� �
� �
2 0 1 0 5
2 3 22
q q q .q
F F k 3k 36.10 N
a
2 3
a
3 2
−
= = = =
� �
� �
� �
;
0
23 2 2
F 2F cos120 F= =
V y F = 2Fậ1 = 72.10-5N
Bài 14: T i ba đnh c a m t tam giác đu, ng i ta đt ba đi n tích gi ng nhauạ ỉ ủ ộ ề ườ ặ ệ ố
q1=q2=q3=6.10-7C. H i ph i đt đi n tích th t qỏ ả ặ ệ ứ ư 0 t i đâu, có giá tr bao nhiêu đạ ị ể
h th ng đng yên cân b ng.ệ ố ứ ằ
H ng d n gi i:ướ ẫ ả
Đi u ki n cân b ng c a đi n tích qề ệ ằ ủ ệ 3 đt t i Cặ ạ
13 23 03 3 03
F F F F F 0+ + = + =
r r r r r r
2
0
13 23 3 13 13
2
q
F F k F 2F cos30 F 3
a
= = = =�
có ph ng là phân giác c a góc C. Suy ra ươ ủ
03
F
r
cùng giá ng c chi u v i ượ ề ớ
.
Xét t ng t v i qươ ự ớ 1, q2 suy ra q0 ph i n m t i tâm c a tam giác.ả ằ ạ ủ
2
07
03 3 0
22
q q q
F F k k 3 q 3, 46.10 C
a
2 3
a
3 2
−
= = = −� �
� �
� �
� �
Bài 15: Hai qu c u nh gi ng nhau đc treo vào m t s i dây nh , cách đi n và không giãn. Kho ng cách gi a các qu c u là 4ả ầ ỏ ố ượ ộ ợ ẹ ệ ả ữ ả ầ
cm. Tính l c căng c a các đo n ch n i các qu c u n u các qu c u này mang đi n tích cùng đ l n 4.10ự ủ ạ ỉ ố ả ầ ế ả ầ ệ ộ ớ -8C, kh i l ng m i quố ượ ỗ ả
c u là 1 g. L y g = 10 m/sầ ấ 2, kh o sát hai tr ng h p:ả ườ ợ
a. Hai đi n tích cùng d u.ệ ấ
b. Hai đi n tích trái d u.ệ ấ
H ng d n gi i:ướ ẫ ả
a. Khi hai đi n tích cùng d u: Xét các l c tác d ng lên qu c u phía d i, ta có: ệ ấ ự ụ ả ầ ướ
( )
2
2
22
q
T F mg k mg 1,9.10 N .
BC
−
= + = + =
b. Khi hai qu c u tích đi n trái d u: ả ầ ệ ấ
5
A
O
F2 F3
B C
F1 F23
F
q1 A
O
q0
F03
B C F23
F13 F3