ĐIỆ N XOAY CHIỀ U
ĐIỆ N XOAY CHIỀU TỔNG HỢP
Câu 1: Cho hai hộp kín X, Y chỉchứa 2 trong ba phần tử: R, L
(thuần), C mắc nối tiếp. Khi mắ c hai điể m A, M vào hai cực của
một nguồ n điệ n một chiều thì Ia= 2(A), UV1 = 60(V). Khi mắc hai
điể m A, B vào hai cực của một nguồ n điện xoay chiều tần số50Hz
thì Ia= 1(A), Uv1 = 60V; UV2 = 80V,UAM lệch pha so với UMB một góc 1200, xác đị nh X, Y và các giá trị
của chúng.
Giả i:
* Vì X cho dòng điệ n một chiề u đi qua nên X không chứ a tụ điệ n. Theo đề bài thì X chứa 2 trong ba phần
tửnên X phải chứ a điệ n trởthuần (RX) và cuộn dây thuần cảm (LX). Cuộn dây thuần cảm không có tác
dụng với dòng điệ n một chiều nên: RX=
60
130( )
2
UV
I= = Ω
* Khi mắc A, B vào nguồ n điệ n xoay chiều:ZAM =
60 2 2
160( )
1
UV
R Z
X L
IX
= = Ω = +
2 2 2
60 30 3.30 30 3( )
X
Z Z
L L
X
⇒ = − = ⇒ = Ω
; tanϕAM =
0
3 60
X
X
ZL
AM
R
= ⇒ =
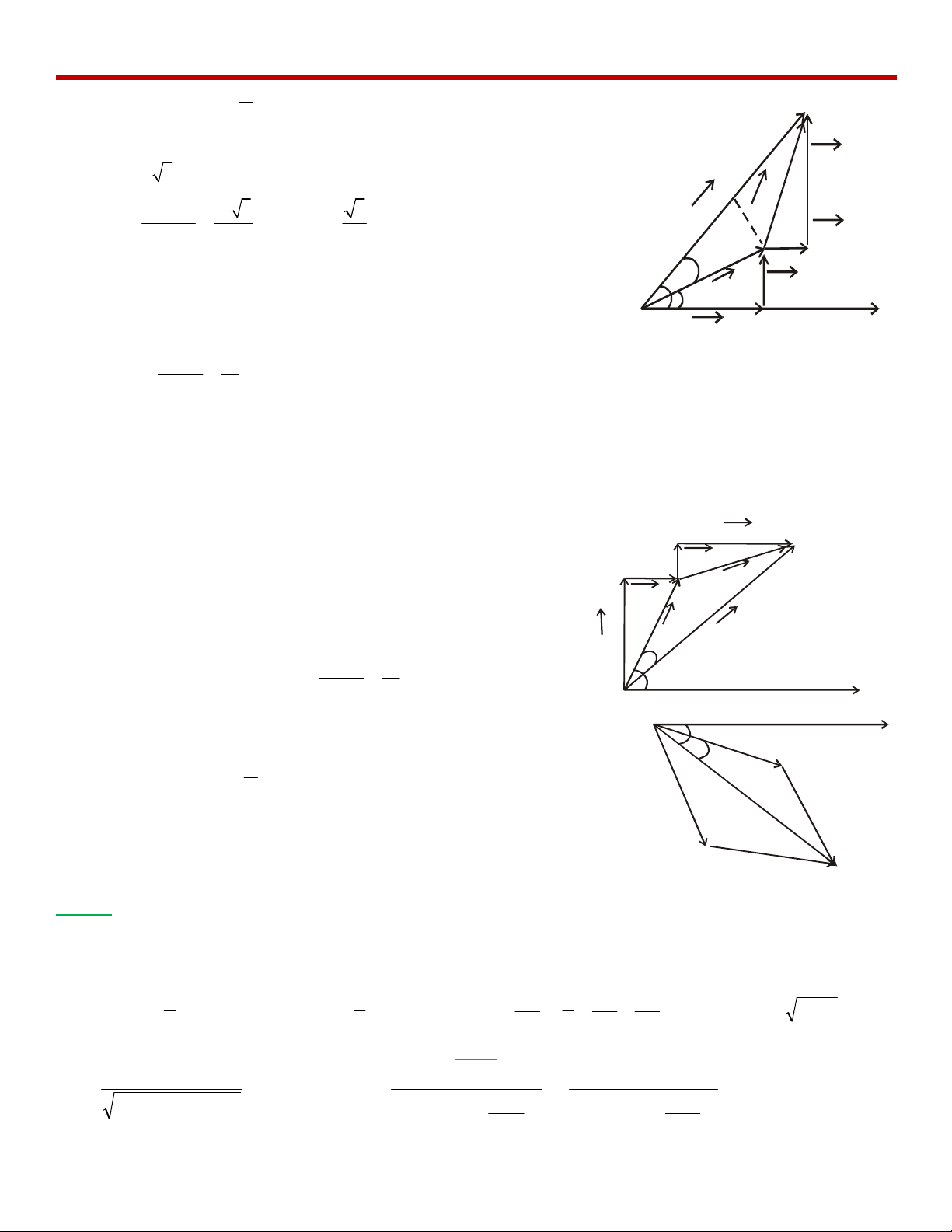
* Vẽgiả n đồ véc tơ cho đoạ n AM. Đoạ n mạ ch MB tuy chư a biế t như ng chắ c chắn trên giả n đồ nó là một
véctơ tiế n theo chiều dòng điệ n, có độ dài =
2
V
U
= 80V và hợp vớ i véc tơ
AB

một góc 1200⇒ta vẽ đư ợ c
giả n đồ véc tơ cho toàn mạ ch
.Từgiả n đồ véc tơ ta thấ y
MB
buộc phải chéo xuống thì mới
tiến theo chiều dòng điệ n, do đó Y phả i chứ a điệ n trởthuần (RY)
và tụ điệ n CY.
+ Xét tam giác vuông MDB
40 40( )
1
UR
Y
RYI
⇒ = = = Ω
3
0
cos30 80. 40 3( ) 40 3( )
2
40 3 0,4 3 ( )
100
U U V Z
L MB L
Y Y
L H
Y
= = = ⇒ = Ω
⇒ = =
Câu 2: Một mạ ch điệ n xoay chiề u có sơ đồ như hình vẽ.Trong hộp
X và Y chỉcó một linh kiện hoặ c điệ n trở, hoặc cuộn cảm, hoặc là tụ
điệ n. Ampe kếnhiệt (a) chỉ1A; UAM = UMB = 10VUAB = 10
V3
.
Công suất tiêu thụcủ a đoạ n mạch AB là P = 5
6
W. Hãy xác đị nh linh kiệ n trong X và Y và độ lớn của
các đạ i lư ợ ng đặ c trư ng cho các linh kiệ n đó. Cho biế t tần sốdòng điệ n xoay chiều là f = 50Hz.
Giải:
Hệsốcông suất:
cos P
UI
=
5 6 2
cos 2 4
1.10 3
⇒ = = ⇒ = ±
AB
MY
aX
v1v2
i
UAM
Ulx
Urx
A
M
AM
600
i
A
Ury
UAB
Urx
Ucy
UAM
MD
UMB
Ulx
300
B
300
30
0
120
0
AB
MY
aX
ĐIỆ N XOAY CHIỀ U
Tr.hợp 1: uAB sớm pha
4
so với i⇒giả n đồ véc tơ
Vì:
3
U UMB
AM
U U
AB AM
=
=
⇒ ∆AMB là ∆cân và UAB = 2UAMcosα
⇒cosα=
10 3
2 2.10
UAB
UAM
=
⇒cosα=
0
330
2
⇒ =
a. uAB sớ m pha hơ n uAM một góc 300
⇒UAM sớ m pha hơ n so vớ i i 1 góc ϕX= 450- 300= 150
⇒X phải là 1 cuộn cảm có tổng trởZXgồ m điệ n trởthuận RXvà độ tự
cảm LX
Ta có:
10 10( )
1
UAM
ZXI
= = = Ω
.Xét tam giác AHM:
+
0 0
cos15 cos15U U R Z
R X X X
X= ⇒ =
⇒RX= 10.cos150= 9,66(Ω)
+
0 0 0
sin15 sin15 10sin15 2,59( )U U Z Z
L X L X
X X
= ⇒ = = = Ω
2,59 8, 24( )
100
L mH
X
⇒ = =
Xét tam giác vuông MKB:
MBK
= 150(vì đố i xứng)⇒UMB sớm pha so với i một góc ϕY= 900- 150= 750
⇒Y là một cuộn cảmcó điệ n trởRYvà độ tựcảm LY
+ RY=
X
ZL
(vì UAM = UMB. ⇒RY= 2,59(Ω)
+
YX
Z R
L=
= 9,66(Ω)⇒LY= 30,7m(H)
b. uAB trễ pha hơ n uAM một góc 300
Tư ơ ng tự ta có:
+ X là cuộn cảm có tổng trởZX=
10 10( )
1
UAM
I= = Ω
Cuộn cả m X có điệ n trởthuần RXvà độ tựcảm LXvới RX= 2,59(Ω);
RY=9,66(Ω)
* Tr.hợp 2: uAB trễpha
4
π
so vớ i i, khi đó uAM và uMB cũng trễ pha hơ n i
(góc 150và 750). Như vậ y mỗi hộp phải chứa tụ điệ n có tổng trởZX, ZX
gồ m điệ n trởthuần RX, RYvà
dung kháng CX, CY. Tr.hợp này không thểthoảmãn vì tụ điệ n không có
điệ n trở.
Câu 2: Đặ t điệ n áp xoay chiều u=U0cosωt (U0không đổ i và ωthay đổ i đư ợ c) vào hai đầ u đoạ n mạch gồm
điệ n trởthuần R,cuộn cảm thuầ n có độ tựcảm L và tụ điệ n có điệ n dung C mắc nối tiếp,vớiCR2< 2L. Khi
ω=ω1hoặcω=ω2thì điệ n áp hiệu dụng giữ a hai đầ u cuộn cảm có cùng một giá trị.Khi ω=ω0thì điệ n áp
hiệu dụng giữ a hai đầ u cuộn cảm có giá trịcự c đạ i.Hệthức liên hệgiữaω1,ω2và ω0là :
A.
)(
2
12
2
2
1
2
0
+=
B.
)(
2
1
210
+=
C.
2
0
1
=
2
1
(
2
1
1
+
2
2
1
)D. ω0=
21
Giải:
UL=
22 )( CL
L
ZZR
UZ
−+
. Do UL1 = UL2 ⇒
2
1
1
2
2
1
)
1
(C
LR
−+
=
2
2
2
2
2
2
)
1
(C
LR
−+
i
M
URX
ULX
K
U
A
B
U
Y
URY
ULY
AH
B
4
5
03
0
0
1
5
0
U
i
B
K
M
H
A
UAB
URY
UX
ULY
URX
ULX
300
450
UY
450
300
A
M
M’ B
i
ĐIỆ N XOAY CHIỀ U
⇒
2
1
22
C
L
R−
+
24
1
1
C
=
2
2
22
C
L
R−
+
24
2
1
C
⇒(2
C
L
- R2)(
2
2
1
-
2
1
1
) =
24
2
1
C
-
24
1
1
C
⇒(2
C
L
- R2) =
2
1
C
2
2
2
1
2
2
2
1
+
⇒
2
1
1
+
2
2
1
= C2(2
C
L
- R2) (1)
UL= ULmax khi
2
22
C
L
R−
+
24
1
C
+ L2có giá trịcực tiểu. ⇒
2
0
1
=
2
2
C
(2
C
L
- R2) (2)
Từ(1) và (2) suy ra:
2
0
1
=
2
1
(
2
1
1
+
2
2
1
) . Chọ n đáp án C. (Vớ i điề u kiện CR2< 2L)
Câu 3: Cho mạ ch điệ n như hình vẽ. Cuộ n dây có độ tựcảm
3
L
=
H, điệ n trởthuần r = 100Ω. Đặ t vào hai đầ u đoạ n mạch một
điệ n áp
100 2 cos100
AB
u t
=
(V). Tính giá trịcủ a C để vôn kếcó
giá trịlớn nhất và tìm giá trịlớn nhấ t đó củ a vôn kế.
A.
4
4 3 .10C
−
=
F và
max 120
C
U=
V. B.
4
3.10
4
C
−
=
F và
max 180
C
U=
V.
C.
4
3.10
4
C
−
=
F và
max 200
C
U=
V. D.
4
3.10C
−
=
F và
max 220
C
U=
V.
Giải.
Ta có:
3
100 . 100 3
L
Z L
= = = Ω
.
( )
2
2
2 2
m ax
100 100 3 400
100 3 3
L
C C
L
r Z
U Z Z
+
+
⇔ = = = Ω
.
4
1 1 3.10
400 4
100 . 3
C
CZ
−
⇒ = = =
F.
( )
2
2
2 2
max
100 100 100 3 200
100
L
C
U r Z
UR
+
+
= = =
V.
Câu 4: Cho đoạ n mạ ch điệ n xoay chiều ANB ,tần sốdòng điệ n 50Hz, đoạ n AN chứa R=10
3
Ω
và C
thay đổ i ,đoạ n NB Chứa L=
2.0
H . Tìm C để
AN
U
cự c đạ i :
A. 106
F
B. 200
F
C. 300
F
D. 250
F
Giải:
Dùng công thức: Khi
2 2
4
2
L L
C
Z R Z
Z+ +
=
thì
ax 2 2
2 R
4
RCM
L L
U
U
R Z Z
=+ −
= UAN
Lư u ý: R và C mắc liên tiếp nhau; Z L= ω.L = 100π.0,2/π=20Ω
Tính :
2 2
4
2
L L
C
Z R Z
Z+ +
=
=
2 2
20 4(10 3) 20 20 1200 400 30
2 2
+ + + +
= = = Ω
L,r
M
C
V
B
A
C
A
B
R
L,r
N
ĐIỆ N XOAY CHIỀ U
Mà
3
1 1 1 10 ( )
. 100 .30 3
C
C
Z C F
C Z
−
= ⇒ = = =
= 106
F
.
Câu 5: Cho đoạ n mạ ch điệ n xoay chiề u ANB ,đoạ n AN chứ a R và C thay đổ i ,đoạ n NB Chứa L=
5.1
H .
Biết f = 50Hz ,ngư ờ i ta thay đổ i C sao cho
AN
U
cự c đạ i bằng 2
AB
U
.Tìm R và C:
A.
C
Z
=200
Ω
; R=100
Ω
B.
C
Z
=100
Ω
; R=100
Ω
C.
C
Z
=200
Ω
; R=200
Ω
D.
C
Z
=100
Ω
; R=200
Ω
Giải:
Khi
2 2
4
2
L L
C
Z R Z
Z+ +
=
thì
ax 2 2
2 R
4
RCM
L L
U
U
R Z Z
=+ −
Lư u ý: R và C mắc liên tiếp nhau
Đề cho
AN
U
cự c đạ i bằng 2
AB
U
suy ra:
2 2
R
14
=+ −
L L
R Z Z
⇒
2 2 2 2 2 2
4 2 4 .+ − + + =
L L L L
R Z Z R Z Z R
2 2 2 2 4 2 2 4 2 2 2
3 2 2 4 9 12( ) 4 4 (4 )
L L L L L L L
R Z Z R Z R R Z Z Z R Z⇔ + = + ⇒ + + = +
4 2 2 2
9 (12 16 ) 0⇔ + − =
L L
R Z Z R
4 2 2
9 4 0⇔ − =
L
R Z R
2 2 2
(9 4 ) 0⇔ − =
L
R Z R
Do R khác 0 nên
2 2
(9 4 ) 0⇔ − =
L
R Z
2 2 2 2
(9 4 ) 0 150 100
3 3
L L
R Z R Z⇔ − = ⇒ = = = Ω
2 2
4
2
L L
C
Z R Z
Z+ +
=
=
2 2
150 4100 150 200
2
+ +
= = Ω
.
Câu 6: Đặ t mộ t điệ n áp xoay chiều u = U0cosωt (V) vào hai đầ u mộ t đoạ n mạch AB gồ m điệ n trởR, cuộn
dây cảm thuần L và tụ điệ n có điệ n dung C mắc nối tiếp. Tụ C có điệ n dung thay đổ i đư ợ c.Thay đổ i C, khi
ZC= ZC1 thì cư ờ ng độ dòng điệ n trễpha
4
so vớ i điệ n áp hai đầ u đoạ n mạch, khi ZC= ZC2 = 6,25ZC1 thì
điệ n áp hiệu dụng giữa hai tụ đạ t giá trịcự c đạ i. Tính hệsốcông suất của mạch.
A. 0,6 B. 0,8 C. 0,7 D. 0,9
Giải:
tanϕ1=
R
ZZ CL 1
−
= tan(
4
) = 1
⇒
R = ZL–ZC1
⇒
ZC1 = ZL- R
Ta có: UC2 = Ucmax
⇒
ZC2 =
L
L
Z
ZR 22 +
⇒
6,25ZC1ZL= R2+ZL2
⇒
6,25( ZL- R) ZL= R2+ZL2
⇒
5,25ZL2- 6,25RZL–R2= 0
⇒
21ZL2- 25RZL–4R2= 0
⇒
ZL=
3
4R
Ta có: ZC2 =
L
L
Z
ZR 22 +
=
3
49
16 2
2
R
R
R+
=
12
25R
⇒
cosϕ2=
2
Z
R
=
22 )
12
25
3
4
(RR
R
R
−+
=0,8.
Câu 7: Cho mạ ch điệ n RLC, Vớ i C thay đổ i đư ợ c. Điệ n áp đặ t vào hai đầ u đoạ n mạ ch có dạ ng
2cos ( ).u U t V
=
Khi
4
1
10 ( )C C F
−
= =
thì cư ờ ng độ dòng điệ n i trễ pha
4
so vớ i u. Khi
4
2
10 ( )
2,5
C C F
−
= =
thì điệ n áp hai đầ u tụ điệ n đạ t giá trị cự c đạ i. Tính tầ n số góc
. Biế t
2( )L H
=
A.
200 ( / )rad s
B.
50 ( / )rad s
C.
10 ( / )rad s
D.
100 ( / )rad s
Giả i:
ĐIỆ N XOAY CHIỀ U
Khi
4
1
10 ( )C C F
−
= =
thì dòng điệ n i trễ pha
4
so u nên:
RZZ
CL
=−
1
(1)
Khi
4
2
10 ( )
2,5
C C F
−
= =
thì điệ n áp hai đầ u tụ điệ n đạ t giá trịcự c đạ i nên :
L
L
CZ
ZR
Z
22
2
+
=
(2)
thay (1) vào (2) ta có pt:
01010.9
828244
2=+−
(3)
-giả i ta đư ơ c:
100=
rad/s và
2
50
=
Rad/s (loại) vì thay nghiệm này vào (1) thì không thỏa mãn
Câu 7: Cho mạ ch điệ n xoay chiều RLC mắc nối tiế p. Điệ n áp xoay chiề u đặ t vào hai đầ u đoạ n mạch có
biểu thức
u U 2cos t,= ω
tần sốgóc
ω
biế n đổ i. Khi
140 (rad / s)ω = ω = π
và khi
2360 (rad / s)ω = ω = π
thì
cư ờ ng độ dòng điệ n hiệu dụng qua mạ ch điệ n có giá trịbằ ng nhau. Để cư ờ ng độ dòng điệ n trong mạ ch đạ t
giá trịlớn nhất thì tần sốgóc
ω
bằng
A. 100
π
(rad/s). B. 110
π
(rad/s).
C. 200
π
(rad/s). D. 120
π
(rad/s).
Giải :
Cách 1:Nhớcông thức:Vớiω=ω1hoặcω=ω2thì I hoặcPhoặc URcó cùng một giá trịthì IMax hoặc PMax
hoặc URMax
khi đó ta có:
1 2
=
=120
π
(rad/s). Chọn D
Cách 2:I1= I1
⇒
Z1= Z1
⇒
(ZL1 –ZC1)2= (ZL2 –ZC2)2
Do ω1≠ ω2nên (ZL1 –ZC1) = - (ZL2 –ZC2)
⇒
ZL1 + ZL2 = ZC1 + ZC2
(ω1+ω2)L =
C
1
(
1
1
+
2
1
)
⇒
LC =
21
1
(1)
Khi I = Imax; trong mạch có cộ ng hư ở ng LC =
2
1
(2).
Từ(1) và (2) ta có =
21
=120(rad/s).
Câu 8: Đặ t mộ t điệ n áp u = U0cos
tω
( U0không đổ i,
ω
thay đổ i đư ợ c) vào 2 đầ u đoạ n mạch gồm R, L, C
mắc nối tiếp thỏa mãn điề u kiện: CR2< 2L. Gọi V1,V2, V3lầ n lư ợ t là các vôn kếmắ c vào 2 đầ u R, L, C.
Khi tăng dầ n tần sốthì thấy trên mỗi vôn kế đề u có 1 giá trịcự c đạ i, thứtựlầ n lư ợ t các vôn kếchỉgiá trị
cự c đạ i khi tăng dầ n tần sốlà
A. V1, V2, V3.B. V3, V2, V1.C. V3, V1, V2.D. V1, V3,V2.
Giải:
Ta gọi sốchỉcủa các vôn kếlà U: U1=IR =
22 )
1
(C
LR
UR
−+
U1= U1max khi trong mạch có sựcộ ng hư ở ng điệ n:
⇒
ω2=
LC
1
(1)
U2= IZL=
2
2
2
22
22222 2
1
)
1
(y
U
C
L
C
LR
UL
C
LR
LU =
−++
=
−+
U2= U2max khi y2=
2
2
2
42
2
11 L
C
L
R
C+
−
+
có giá trịcực tiểu y2min