Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN: 978-604-82-1710-5
68
ĐIỀU CHỈNH TRẠNG THÁI ỨNG SUẤT
TRONG THÂN ĐẬP BÊ TÔNG TRỌNG LỰC
THEO PHƯƠNG PHÁP PHẦN TỬ HỮU HẠN
Hà Thanh Dương, Nguyễn Quang Hùng, Vũ Hoàng Hưng
Đại học Thủy lợi, email: congty3t@gmail.com
1. ĐẶT VẤN ĐỀ
Hiện nay phương pháp phần tử hữu hạn
(PTHH) đã trở thành phương pháp phổ biến
trong phân tích ứng suất – biến dạng kết cấu
công trình. Trong phân tích đập trọng lực,
phương pháp này ưu điểm hơn phương pháp
sức bền vật liệu (SBVL) khi tính toán kết cấu
có hình dạng phức tạp, kết cấu trên nền đàn
hồi hoặc phân tích phi tuyến tính kết cấu.
Tuy nhiên do hạn chế của việc mô hình hóa
kết cấu đập và nền nên phương pháp PTHH
thường cho kết quả ứng suất rất lớn (ứng suất
tập trung) tại các vị trí có đột biến về hình
học hoặc kết cấu và có liên quan đến hình
thức phần tử và kích thước mạng lưới phần
tử. Nếu lấy giá trị ứng suất này làm tiêu
chuẩn khống chế và đánh giá an toàn ứng
suất sẽ không phản ánh đúng sự làm việc
thực tế của đập. Nhiều tác giả đã đề xuất lấy
ứng suất điểm lân cận, hoặc lấy giá trị bình
quân miền ứng suất kéo chính; sử dụng
PTHH tự thích ứng với mô hình h hoặc p, sử
dụng phần tử có khả năng nứt, hoặc cho nền
bị biến dạng dẻo để phân phối lại ứng suất,
giảm ứng suất tập trung. Phương pháp đầu
đơn giản nhưng có nhược điểm là phân bố
ứng suất không thỏa mãn phương trình cân
bằng; phương pháp sau phức tạp và có lượng
tính toán lớn đặc biệt khi phân tích động. Vì
vậy bài báo đề xuất sử dụng phương pháp
phối hợp phương pháp PTHH và phương
pháp SBVL (hay còn gọi là phương pháp ứng
suất tương đương phần tử hữu hạn) trong
phân tích đập bê tông trọng lực để điều chỉnh
lại trạng thái ứng suất trong toàn miền, loại
bỏ ứng suất tập trung nhưng vẫn phản ánh
được ảnh hưởng của các yếu tố được quy
định trong TCVN 9137-2012[[1]] đối với trạng
thái ứng suất – biến dạng trong thân đập.
2. PHƯƠNG PHÁP ỨNG SUẤT TƯƠNG
ĐƯƠNG PTHH
2.1. Nguyên lý tính toán
Phương pháp ứng suất tương đương phần
tử hữu hạn (Finite Element Equivalent Stress
Method) đầu tiên được tác giả người Trung
Quốc đề xuất khi phân tích ứng suất đập
vòm[2], [3] sau đó nhiều tác giả đã ứng dụng và
cải tiến phương pháp[4]~[6]. Tư tưởng cơ bản
của phương pháp là coi ứng suất trên một mặt
cắt ngang nào đó được lấy từ kết quả phân
tích PTHH tương đương với nội lực tác dụng
trên mặt cắt ngang này. Lợi dụng phương
pháp SBVL tính toán phân bố lại ứng suất
trên mặt cắt ngang để loại bỏ ứng suất tập
trung khi tính theo phương pháp PTHH.
2.2. Công thức tính toán
Từ kết quả tính toán phân bố ứng suất theo
phương đứng y bằng phương pháp PTHH,
tính toán nội lực tương đương trên một mặt
cắt ngang bất kỳ với bề rộng bằng 1 đơn vị:
L/2
yy
-L/2
N= σ dx
,
L/2
zy
-L/2
M = xσ dx
(1)
trong đó: N – lực dọc mặt cắt; M – mô men
mặt cắt; L – chiều dài mặt cắt; y - ứng suất
theo phương đứng tại vị trí x.
Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN: 978-604-82-1710-5
69
Với giả thiết ứng suất trên cạnh phần tử là
tuyến tính, từ giá trị ứng suất tại các điểm nút
tính toán nội lực theo công thức dưới đây[7], [8]:
yy
n-1 i i 1 i
i=1
y
Nl
2
=



(2a)
y y y y
n-1 i i 1 i i 1
i i i 1 i o
yy
i=1 i i 1
z2
M l x x x x
23
=







(2b)
trong đó:
y
i
,
y
i1
- ứng suất theo phương
đứng tại điểm nút có vị trí xi và xi+1; li = xi+1 -
xi; xo – vị trí trung tâm mặt cắt ; n - số điểm
nút trên mặt cắt.
Dựa vào công thức tính toán ứng suất của
cấu kiện chịu nén lệch tâm thu được ƯSTĐ
từ kết quả PTHH:
(3)
trong đó:
'y
i
- ƯSTĐ PTHH tại vị trí xi;
I - mô men quán tính của mặt cắt đối với xo.
2.3. So sánh kết quả tính toán ứng suất
đáy đập theo các phương pháp
Tiến hành phân tích đập trọng lực cao
H=100m, bề rộng đáy 70m, bề rộng đỉnh
10m; Mực nước thượng lưu 95m. Phạm vi
nền tính toán lấy về mỗi phía bằng 1,5 lần
chiều cao đập. Kích thước phần tử bằng
3,5m. Tham số vật liệu cho ở bảng 1.
Bảng 1. Tham số vật liệu đập và nền
Tham số
E (kN/m2)
Poisson
(T/m3)
Đập
2,65×107
0,173
2,450
Nền
Eđ(*)
0,250
2,700
(*) Giả thiết En=
Eđ
Để có cơ sở so sánh với phương pháp
SBVL, giả thiết nền tuyệt đối cứng (lấy giá
trị = 1000). Kết quả tính toán ứng suất theo
phương đứng trên mặt cắt đáy đập theo 3
phương pháp cho ở bảng 2 và hình 1.
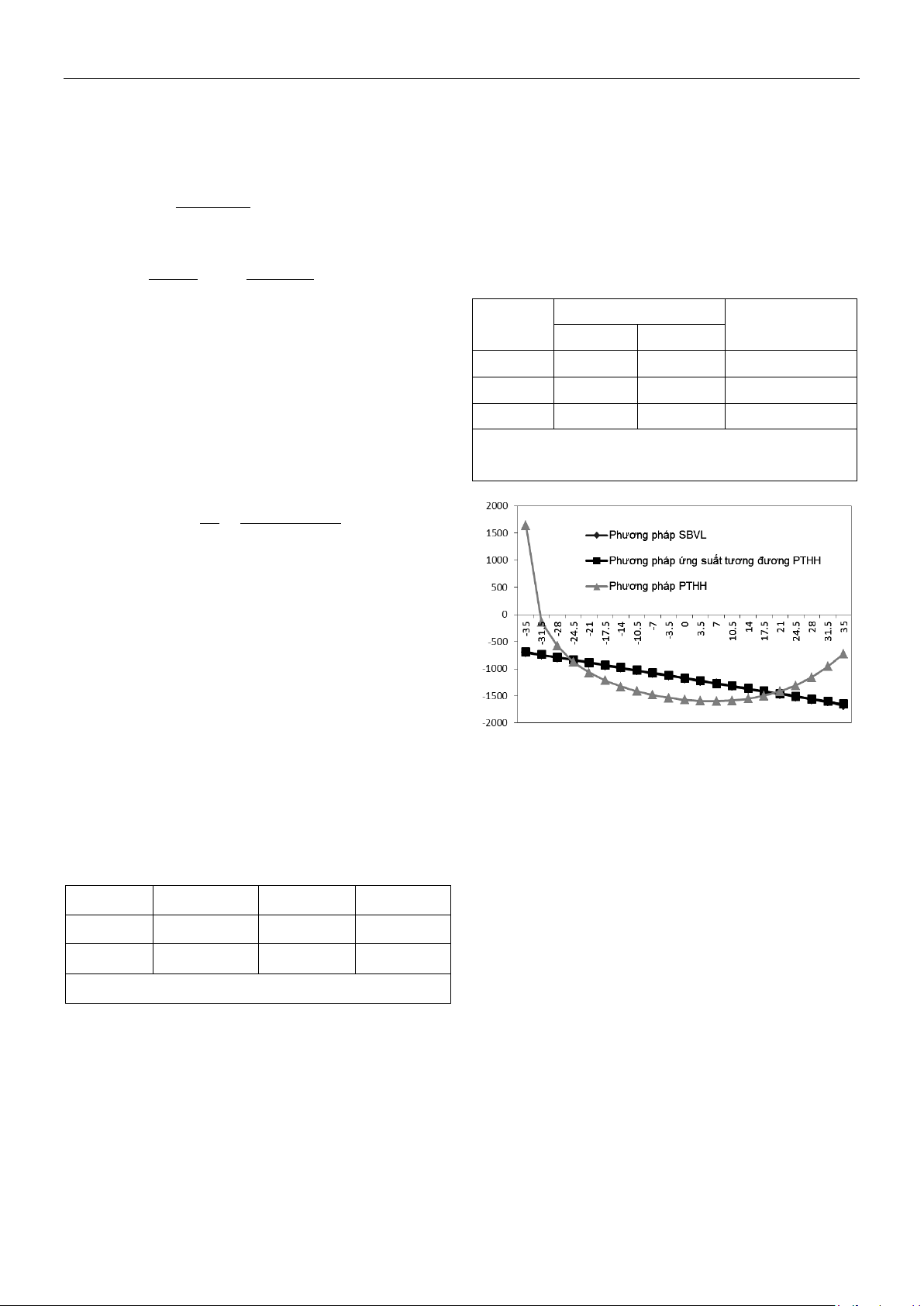
Từ kết quả ở bảng 2 và hình 1 cho thấy
tính toán theo phương pháp PTHH cho giá trị
ứng suất cục bộ y tại vị trí chân đập thượng
lưu khá lớn bằng 1642,9kN/m2 (chịu kéo)
trong khi phân bố ƯSTĐ hoàn toàn chịu nén
và chênh lệch không nhiều so với ứng suất
theo SBVL. Sự chênh lệch này liên quan đến
giả thiết cơ bản của SBVL có tính cứng. Các
mặt cắt ngang phía trên đáy đập cũng có quy
luật này nhưng càng lên cao độ chênh lệch
càng giảm dần.
Bảng 2. So sánh kết quả tính toán ứng suất
Phương
pháp
Ứng suất (kN/m2)
Chênh lệch %
với PP SBVL
TL
HL
SBVL
-700,3
-1679,7
-
PTHH
1642,9
-722,8
+334,6(-57,0)
ƯSTĐ
-690,7
-1651,9
-1,4(-1,65)
Giá trị trong () là chênh lệch ứng suất hạ lưu
(+) Ứng suất tăng ; (-) Ứng suất giảm
Hình 1. So sánh kết quả tính toán ứng suất
Kích thước mạng lưới phần tử cũng ảnh
hưởng đến giá trị ƯSTĐ. Khi kích thước
mạng lưới càng nhỏ, ƯSTĐ khá ổn định
(Bảng 3) trong khi kết quả tính toán từ PTHH
thay đổi rất lớn đặc biệt tại vị trí chân đập.
Ngoài ra ƯSTĐ được lấy từ kết quả của
phương pháp PTHH nên phương pháp ƯSTĐ
có thể giải quyết được một vài hạn chế của
phương pháp SBVL như sự khác nhau giữa
đặc trưng cơ học vật liệu đập và nền, sự có
mặt của hành lang, sự phân bố bê tông trong
từng vùng, tính không đồng nhất của nền,
trình tự thi công…
Ví dụ như để xem xét ảnh hưởng của độ
cứng nền đến phân bố ứng suất khi tính toán
theo phương pháp ƯSTĐ đã tiến hành thay
đổi độ cứng nền (thay đổi ). Từ bảng 4 cho
thấy phương pháp ƯSTĐ đã phản ánh được
ảnh hưởng của độ cứng nền đến phân bố ứng
Tuyển tập Hội nghị Khoa học thường niên năm 2015. ISBN: 978-604-82-1710-5
70
suất trong thân đập. Khi độ cứng nền càng
lớn, kết quả tính toán ứng suất sẽ tiệm cận
đến kết quả tính toán theo SBVL.
Bảng 3. So sánh kết quả tính toán khi kích
thước mạng lưới phần tử thay đổi
Mạng
lưới
Nội lực
Ứng suất y
(kN/m2)
N(kN)
M(kNm)
TL
HL
3,5m
-81993
-392479
-690
-1652
1,75m
-82644
-396971
-694
-1667
0,825m
-82971
-398389
-697
-1673
Bảng 4. Ảnh hưởng của độ cứng nền
TT
Hệ số độ cứng
nền
Ứng suất y (kN/m2)
TL
HL
1
1000
-690,7
-1651,9
2
1
-687,8
-1654,9
3
0,01
-683,1
-1659,5
3. ĐIỀU CHỈNH TRẠNG THÁI ỨNG
SUẤT ĐẬP TRỌNG LỰC BẰNG ANSYS
Bản thân phần mềm ANSYS không có mô
đun phân tích ƯSTĐ. Thông thường sau khi
phân tích ứng suất đập trọng lực theo phương
pháp PTHH, tiến hành xuất ứng suất tại các
mặt cắt ngang, sau đó sử dụng công thức (2)
tính toán ra nội lực mặt cắt và sử dụng công
thức (3) để xác định ƯSTĐ tại các mặt cắt.
Việc làm này mất khá nhiều thời gian và khó
phân vùng ứng suất cục bộ trên toàn bộ mặt
cắt ngang đập. Bài báo thông qua ngôn ngữ
APDL, tiến hành lập trình tính toán để tự
động xuất ƯSTĐ tại các điểm nút trên mặt
cắt từ đó vẽ đường đẳng trị từ các điểm ứng
suất này. Kết quả tính toán cho dưới dạng
bảng biểu, phổ màu, hoặc đường đẳng trị trên
toàn bộ mặt cắt ngang.
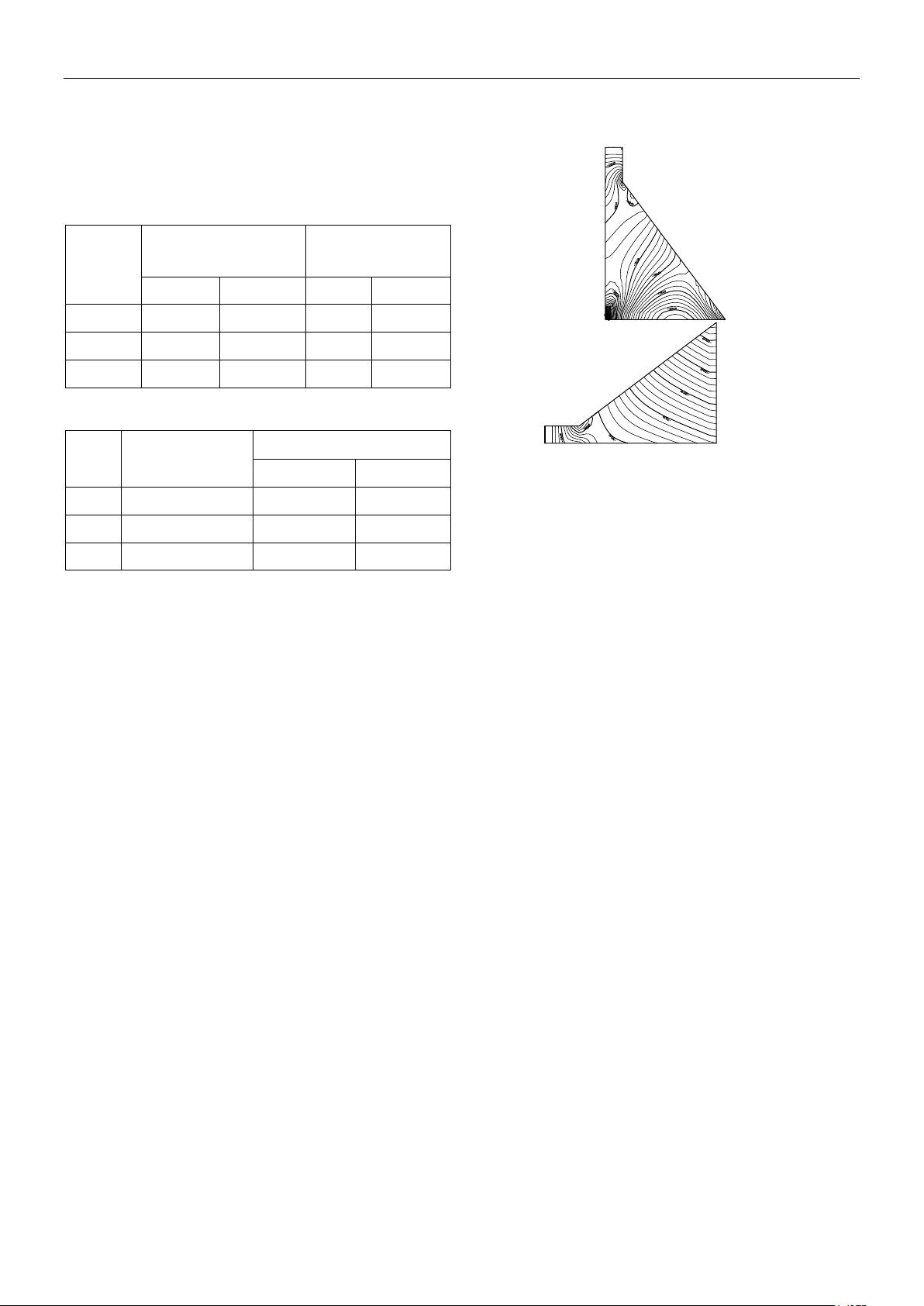
Ví dụ với mặt cắt đập cho ở mục 2 và tham
số vật liệu cho ở bảng 1 khi En = 8,23×106
kN/m2, tiến hành phân tích ƯSTĐ y trên
mặt cắt ngang đập trọng lực. Kết quả tính
toán cho ở hình 2 dưới dạng đường đẳng trị
trong hai trường hợp tính toán theo phương
pháp PTHH (hình 2a) và phương pháp ƯSTĐ
(hình 2b). Từ hình 2 cho thấy sau khi tính
toán ƯSTĐ đã loại bỏ được vùng ứng suất
cục bộ tại chân đập.
a) b)
Hình 2. Kết quả tính toán ứng suất đập
4. KẾT LUẬN
Kết quả tính toán ƯSTĐ đã loại bỏ được
hiện tượng tập trung ứng suất tại vị trí góc
đập trọng lực khi tính toán theo phương pháp
PTHH, ứng suất thu được khá ổn định và đã
cơ bản giải quyết vấn đề ứng suất chân đập
thay đổi khi mạng lưới phần tử thay đổi. Kiến
nghị trong phân tích độ bền đập bê tông trọng
lực cần bổ sung tính toán ƯSTĐ.
5. TÀI LIỆU THAM KHẢO
[1] Tiêu chuẩn Việt Nam, Công trình thủy lợi –
Thiết kế đập bê tông và bê tông cốt thép, TCVN
9137-2012.
[2] 朱伯芳 (1988), 国际拱坝学术讨论会
综述,水利发电, 1988, 8, 49-52.
[3] 博作新 (1989), 有限元法在拱坝设计中的
应用, 河海大学学报, 1991, 2, 8-15.
[4] 李同春, 温召旺 (2002), 拱坝应力分析中
的有限元内力法, 水力发电学报, 79(4): 18-
24.
[5] 李同春，章杭惠 (2004), 改进的拱坝等
效应 力分析方法, 河海大学学报, 31(1),
104-107.
[6] 李同春, 陈会芳, 章杭惠, 王仁坤 (2004),
网格尺寸对拱坝等效应力分析的影响,
水利学报, 9, 83-87.