Ch ng 4 ươ ĐO ĐI N TRỆ Ở
3.1 ĐO ĐI N TR B NG VÔN K VÀ AMPE K Ệ Ở Ằ Ế Ế
Đi n tr là m t trong nh ng đi l ng đi n quan tr ng . Ng i ta phân lo iệ ở ộ ữ ạ ượ ệ ọ ườ ạ
đi n tr theo giá tr Ohm c a chúng , đi n tr đc phân thành 3 c p ệ ở ị ủ ệ ở ượ ấ
Đi n tr có giá tr l n là đi n tr có giá tr t 0.1Mệ ở ị ớ ệ ở ị ừ tr lên ở
Đi n tr có giá tr trung bình t 1Kệ ở ị ừ đn 0.1Mế
Đi n tr có giá tr nh t 1Kệ ở ị ỏ ừ tr xu ng ở ố
Theo đnh lu t Ohm , ta có R = ị ậ
Nh v y đ xác đnh giá tr đi n tr ta s d ng ampe k và volt k . ư ậ ể ị ị ệ ở ử ụ ế ế Ở
ph ng pháp này , ta xác đnh giá tr đi n tr đang ho t đng ( đo nóng ) theo yêuươ ị ị ệ ở ạ ộ
c u . ầ
Có hai cách đu m ch là ấ ạ
“ M c r dài “ hay “Ampe k m c sau “ . Nghĩa là m c volt k tr c –ắ ẽ ế ắ ắ ế ướ
ampe k m c sau ế ắ
“ M c r ng n “hay “ampe k m c tr c “ . Nghĩa là m c ampe k tr cắ ẽ ắ ế ắ ướ ắ ế ướ
– volt k m c sau ế ắ
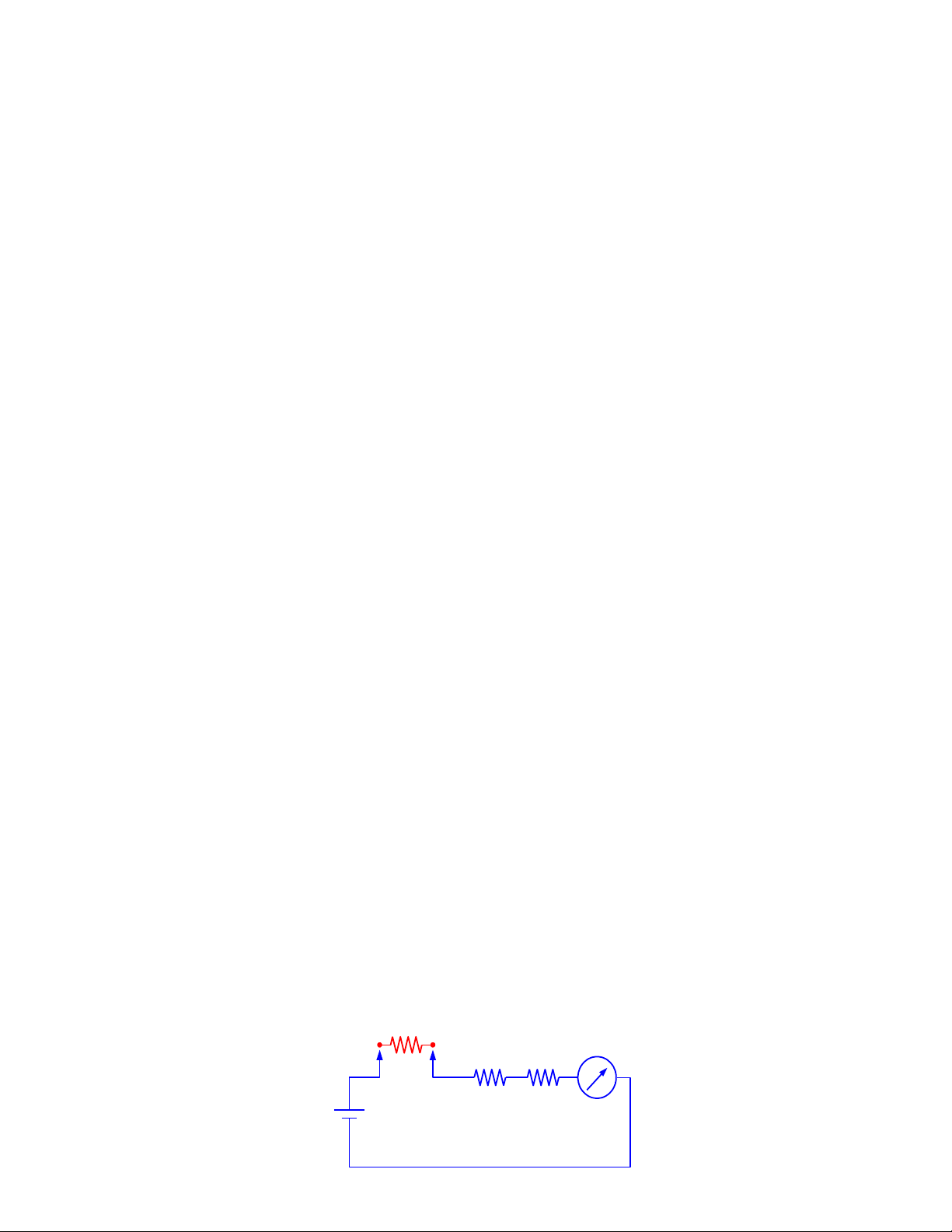
3.1.1 M c r ng n ( ampe k m c tr c ) ắ ẽ ắ ế ắ ướ
Do volt k m c song song v i đi n tr t i nên ta có ế ắ ớ ệ ở ả
IA = IV + IR
N u IếR >> IV thì sai s do nh h ng c a volt k không đáng k ố ả ưở ủ ế ể
Th t v y , n i tr c a volt k và đi n tr t i đi n tr t ng đng đc xácậ ậ ộ ở ủ ế ệ ở ả ệ ở ươ ươ ượ
đnh ị
Mắc rẽ dai
A
RX
V
U
A
RX
V
U
Mắc rẽ ngăn
RX’ = =
Sai s t ng đi c a phép đo (%) ố ươ ố ủ
% = 100% = ( - 1 ) 100%
Đ sai s (% nh nh t thì bi u th c ( 1 + ) ể ố ỏ ấ ể ứ 1
Nghĩa là 0 hay RV >> RX
Nh v y ph ng pháp này đc s d ng trong tr ng h p đi n tr c n đoư ậ ươ ượ ử ụ ườ ợ ệ ở ầ
RX có giá tr nh ho c volt k có n i tr l n ị ỏ ặ ế ộ ở ớ
3.1.2 M c r dài ( Ampe k m c sau ) ắ ẽ ế ắ
Do ampe k m c n i ti p v i đi n tr c n đo nên t ng tr đc xác đnhế ắ ố ế ớ ệ ở ầ ổ ở ượ ị
theo bi u th c ể ứ
RX’ = RA + RX hay U = UA + URX
Sai s t ng đi c a phép đo ố ươ ố ủ
% = = 100%
Đ gi m thi u sai s t ng đi ể ả ể ố ươ ố % thì RX >> RA ( nghĩa là URX >> UA )
Nh v y ph ng pháp này đc s d ng trong tr ng h p đi n tr c n đoư ậ ươ ượ ử ụ ườ ợ ệ ở ầ
có giá tr l n ho c ampe k có n i tr nh ị ớ ặ ế ộ ở ỏ
3.1.3 Ph ng pháp so sánh ươ
ph ng pháp này , ng i ta th ng dùng c u đo Wheatstone đ xác đnhỞ ươ ườ ườ ầ ể ị
giá tr đi n tr đc chính xác h n và th ng đc dùng trong phòng thí nghi m vìị ệ ở ượ ơ ườ ượ ệ
nh ng u đi m c a nó ữ ư ể ủ
Có hai ph ng pháp đo là ươ
Ph ng pháp cân b ng ươ ằ
Ph ng pháp không cân b ng ươ ằ
3.2 ĐO ĐI N TR B NG OHM K Ệ Ở Ằ Ế
3.2.1 S đ m ch đi n đo đi n tr ơ ồ ạ ệ ệ ở
Trong đng h đo v n năng còn cò tên g i khác là multimeter VOM , đây làồ ồ ạ ọ
lo i đng h dùng đ đo đi n áp , dòng đi n và đi n tr . trong tr ng h p dùngạ ồ ồ ể ệ ệ ệ ở ườ ợ
Ohm k đ đo đi n tr thì tr ng thái đo là ph n t đi n tr đo Rế ể ệ ở ạ ầ ử ệ ở X không có năng
l ng ( đo ngu i ) m ch đo s s d ng ngu n pin riêng ượ ộ ạ ẽ ử ụ ồ
R
X
E
R
1
R
m
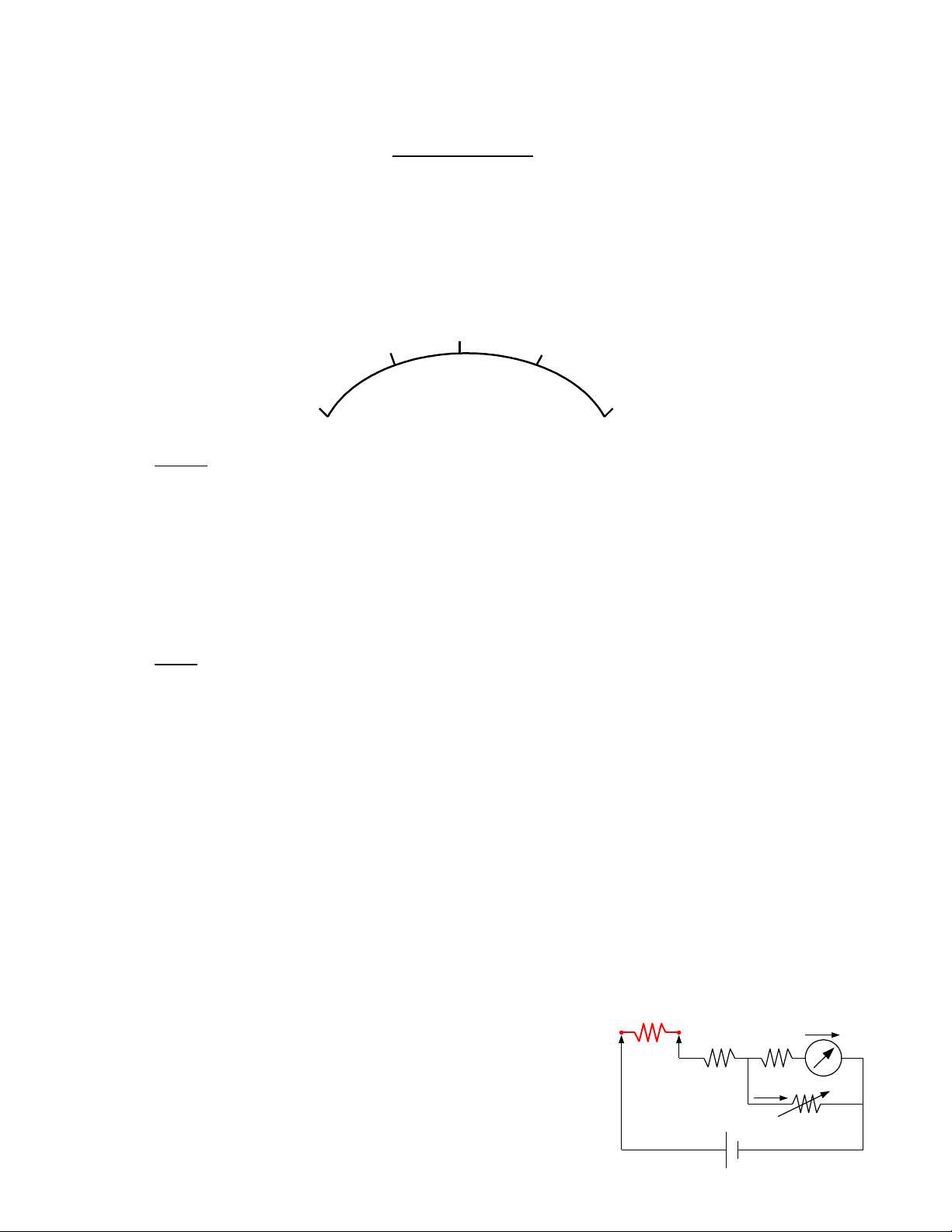
Đây là m ch Ohm k m c n i ti p , dòng đi n qua c c u ch th Iạ ế ắ ố ế ệ ơ ấ ỉ ị m
R1 đi n tr chu nệ ở ẩ
c a t m đo.ủ ầ
Rm đi n tr n i c a c c u.ệ ở ộ ủ ơ ấ
Khi Rx 0 , Im Imax ( dòng c c đi c a c c u t đi n )ự ạ ủ ơ ấ ừ ệ
Khi Rx , Im 0 ( không có dòng qua c c u )ơ ấ
Ví d ụ
Cho m ch đo đi n tr nh hình v . Bi t r ng đi n áp ngu n pin là Eạ ệ ở ư ẽ ế ằ ệ ồ b = 1.5V
và R1 + Rm = 15 k - Imax = 100A
a. Xác đnh đ l ch kim c a c c u đo khi ị ộ ệ ủ ơ ấ
b. RX đc n i t t ượ ố ắ
c. Xác đnh giá tr đi n tr Rị ị ệ ở X khi kim c c u đo l ch ½ Dơ ấ ệ m
Gi i ả
T s đ trên , ta nh n th y khi Rừ ơ ồ ậ ấ X = 0 ( n i t t ) thì dòng đi n qua c c u đoố ắ ệ ơ ấ
có giá tr l n nh t ( Iị ớ ấ m = Imax )
Th t v y , ta có Iậ ậ m = Imax = = = 100 A
Im = Imax = 100A
Khi kim c c u đo l ch ½ Dơ ấ ệ m , thì dòng đi n qua c c u đo có giá tr là ệ ơ ấ ị
Im = Imax = 50 A
T đó ta xác đnh đc giá tr c a đi n tr ừ ị ượ ị ủ ệ ơ ûRX là
RX = - ( R1 + Rm )
RX = 15 k
3.2.2 M ch đo đi n tr th c t ạ ệ ở ự ế
Trong th c t ngu n pin Eự ế ồ b có th thay đi .ể ổ
Khi Rx 0 , dòng đi n Iệm qua c c u không b ngơ ấ ằ
Imax do đó m ch đo có th m c thêm Rạ ể ắ 2 , bi n tr nàyế ở
dùng đ ch nh đi m ể ỉ ể “0” cho m ch đo khi b Eạ ị b
thay đi . Nh v y, tr c khi đo ta ph i ng n m chổ ư ậ ướ ả ắ ạ
mx
b
m
RRR
E
I
1
15
5
0
45
Thang ño khoâng tuyeán tính cuûa Omh keá
E
R
1
R
m
I
m
I
2
R
2
R
X
AB ( n i t t đi n tr Rố ắ ệ ở X đng tác ch p 2 que đo ) và đi u ch nh Rộ ặ ề ỉ 2 ( nút Adj c aủ
đ h VOM ) đ cho kim ch th c a Ohm k ch ồ ồ ể ỉ ị ủ ế ỉ “0” .
Theo m ch trên dòng Iạb
m21x
b
b
R//RRR
E
I
N u Rế2 // Rm << R1 thì :
1x
b
b
RR
E
I
Nh v y, đi n áp Vư ậ ệ m đc xác đnh ượ ị
mbm
RRIV //
2
Dòng đi n Iệm qua c c u ch th ơ ấ ỉ ị
m
mb
m
m
m
R
RRI
R
V
I//
2
Do đó m i l n đo ta cho ỗ ầ Rx 0 b ng cách đi u ch nh Rằ ề ỉ 2 đ cho ể
Đ cho khi Eểb có s thay đi thì s ch th Rự ổ ự ỉ ị X s không thay đi ẽ ổ
3.2.3 Nguyên lý đo Ohm k tuy n tính ế ế
Thang đo c a Ohm k theo nguyên lý dòng đi n nh đã đ c p trên khôngủ ế ệ ư ề ậ ở
tuy n tính theo đi n tr đo. Do đó các m ch đo Ohm k tuy n tính trong máy đoế ệ ở ạ ế ế
đi n t ch th kim ho c ch th s , chúng ta chuy n tr s đo đi n tr Rệ ử ỉ ị ặ ỉ ị ố ể ị ố ệ ở X sang đi nệ
áp đo VX b ng cách cung c p ngu n dòng đi n I không đi (b t ch p tr s Rx) . Vằ ấ ồ ệ ổ ấ ấ ị ố X
= RX.I .
Sau đó RX đc đo b i m ch đi n áp, Vượ ở ạ ệ X tuy n tính theo RếX
Nh v y, khi ư ậ Rx 0, Vx 0V
Khi Rx , VX giá tr l n nh t c a m ch đoị ớ ấ ủ ạ
Nh v y n u vôn k có đi n tr ch nh máy tr c khi đo, thì ph i ch nh ư ậ ế ế ệ ở ỉ ướ ả ỉ Rx
cho m ch đo. Không ch nh ạ ỉ Rx 0 nh m ch đo dùng nguyên lý dòng trongư ở ạ
ph n tr c ầ ướ
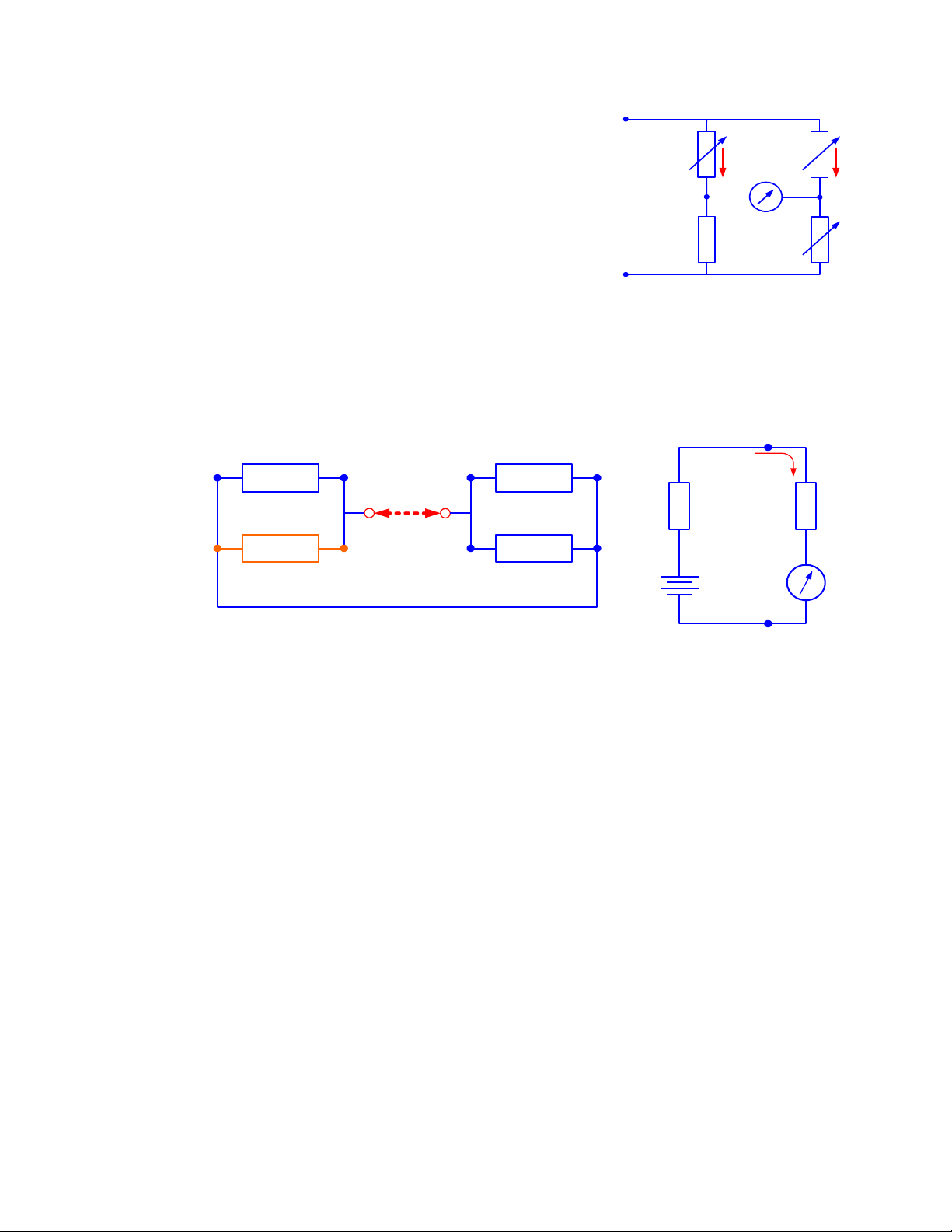
3.3. ĐO ĐI N TR B NG C U ĐOỆ Ở Ằ Ầ
3.3.1 Đo đi n tr dùng c u Wheatstone cân b ng ệ ở ầ ằ
C u Wheatstone đc m c nh hình v . ầ ượ ắ ư ẽ
Trong đó
R1 , R2 , R3 là các đi n tr m u ệ ở ẫ
G là đi n k ch th 0 ệ ế ỉ ị
RX là đi n tr c n đo ệ ở ầ
V n hành ậ
Ta ch nh các giá tr đi n tr Rỉ ị ệ ở 1 , R2 , R3 cho đn khi đi n k G ch zero . Khiế ệ ế ỉ
c u cân b ng , dòng đi n qua đi n k G b ng không ( zero ) nghĩa là Uầ ằ ệ ệ ế ằ C = UA
Hay UR1 = UR2 và URX = UR3
I1 R1 = I2 R2 và I1 RX = I2 R3
Suy ra = hay RX =
V i ph ng pháp đo này Rớ ươ X s đc so sánh v i các đi n tr m u ẽ ượ ớ ệ ở ẫ
Ta nh n th y , k t qu đo đi n tr Rậ ấ ế ả ệ ở X không ph thu c vào ngu n cung c pụ ộ ồ ấ
cho m ch đi n , đây là u đi m c a c u đo Wheatstone . Tuy nhiên ph ng phápạ ệ ư ể ủ ầ ươ
thao tác ph c t p vì ph i đi u ch nh các đi n tr m u nhi u l n và giá tr đi n trứ ạ ả ề ỉ ệ ở ẫ ề ầ ị ệ ở
r
R
1
R
X
R
2
R
3
Ñieän trôû r ngoõ ra
r
G
U
R
- U
S
R
g
I
g
Maïch Thevenin khi taûi laø
r
g
cuûa ñieän keá
R
1
R
2
R
X
R
3
A C
G
I
1
I
2