
Bài tập Tập hợp Q các số hữu tỉ có đáp án
----------------------------------------
Câu 1:
Nhiệt độ lúc 13 giờ ngày 24/01/2016 tại một số trạm đo được cho bởi bảng sau:
Các số chỉ nhiệt độ nêu trên có viết được dưới dạng phân số không?
Lời giải:
Các chỉ số nhiệt độ đã cho trong bảng trên là
−1,3 oC; −0,5 oC; 0,3 oC; −3,1 oC.
Ta có
−1,3=−13
10
;
−0,5=5
10
;
0,3=3
10
;
−3,1=−31
10
Vì các số
−13
10 ;5
10 ;3
10 ;−31
10
là các phân số
nên các số −1,3; −0,5; 0,3; −3,1 viết được dưới dạng phân số.
Vậy các số chỉ nhiệt độ −1,3 oC; −0,5 oC; 0,3 oC; −3,1 oC
viết được dưới dạng phân số.
Câu 2:
Viết các số
−3;0,5;23
7
dưới dạng phân số.
Lời giải:
Trang 1 | 15

Ta có:
−3=−3
1;0,5=5
10 ;23
7=2.7+3
7=17
7
.
Các số
−3
1;5
10 ;17
7
là các phân số.
Vậy các số
−3;0,5;23
7
viết được dưới dạng phân số lần lượt là
−3
1;5
10 ;17
7
.
Câu 3:
Các số 21 ; −12; ; −4,7; −3,05 có là số hữu tỉ không? Vì sao?
Lời giải:
Ta có
21=21
1;− 12=−12
1;− 4,7=−47
10 ;− 3,05=−305
100
Vì các số
21
1;−12
1;−7
−9;−47
10 ;−305
100
có dạng , với , b ≠ 0.
Nên các số
21
1;−12
1;−7
−9;−47
10 ;−305
100
là số hữu tỉ.
Vậy các số
21 ; −12 ;−7
−9; − 4,7; −3,05
là số hữu tỉ.
Câu 4:
Biểu diễn số hữu tỉ
7
10
trên trục số.
Lời giải:
Ta biểu diễn số hữu tỉ
7
10
trên trục số như sau:
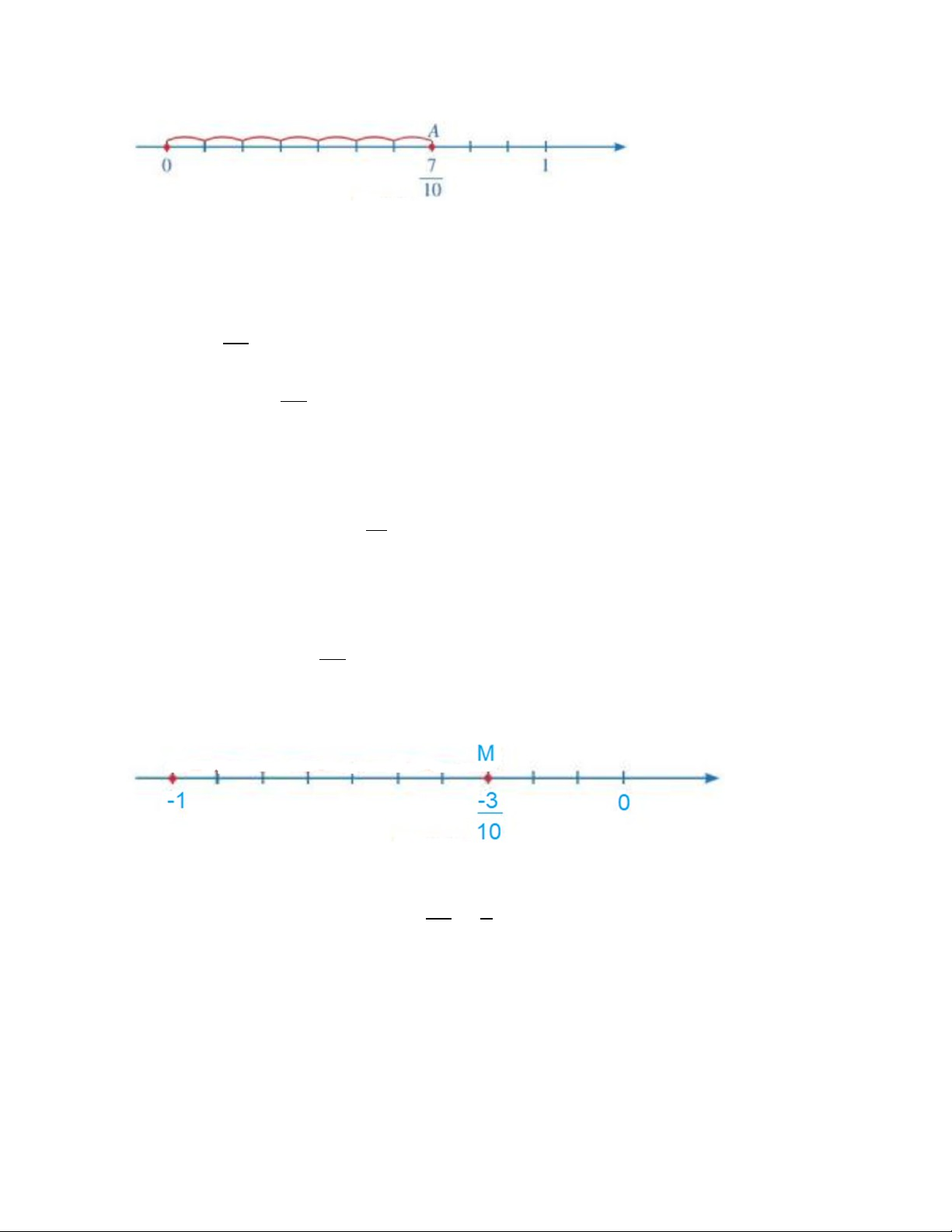
• Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1)
thành mười phần bằng nhau, lấy một đoạn làm đơn vị mới
(đơn vị mới bằng
1
10
đơn vị cũ);
• Đi theo chiều dương của trục số, bắt đầu từ điểm 0, ta lấy ra
7 đơn vị mới đến điểm A. Điểm A biểu diễn số hữu tỉ
7
10
(như hình vẽ).
Trang 2 | 15
Câu 5:
Biểu diễn số hữu tỉ − 0,3 trên trục số.
Lời giải:
Ta có:
−0,3=−3
10
.
Ta biểu diễn số hữu tỉ
−3
10
trên trục số như sau:
• Chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm −1
đến điểm 0) thành mười phần bằng nhau, lấy một đoạn
làm đơn vị mới (đơn vị mới bằng
1
10
đơn vị cũ);
• Đi theo ngược chiều dương của trục số, bắt đầu từ
điểm 0, ta lấy ra 3 đơn vị mới đến điểm M. Khi đó,
điểm M biểu diễn số hữu tỉ
−3
10
.
Vậy điểm M biểu diễn số hữu tỉ − 0,3 (như hình vẽ).
Câu 6:
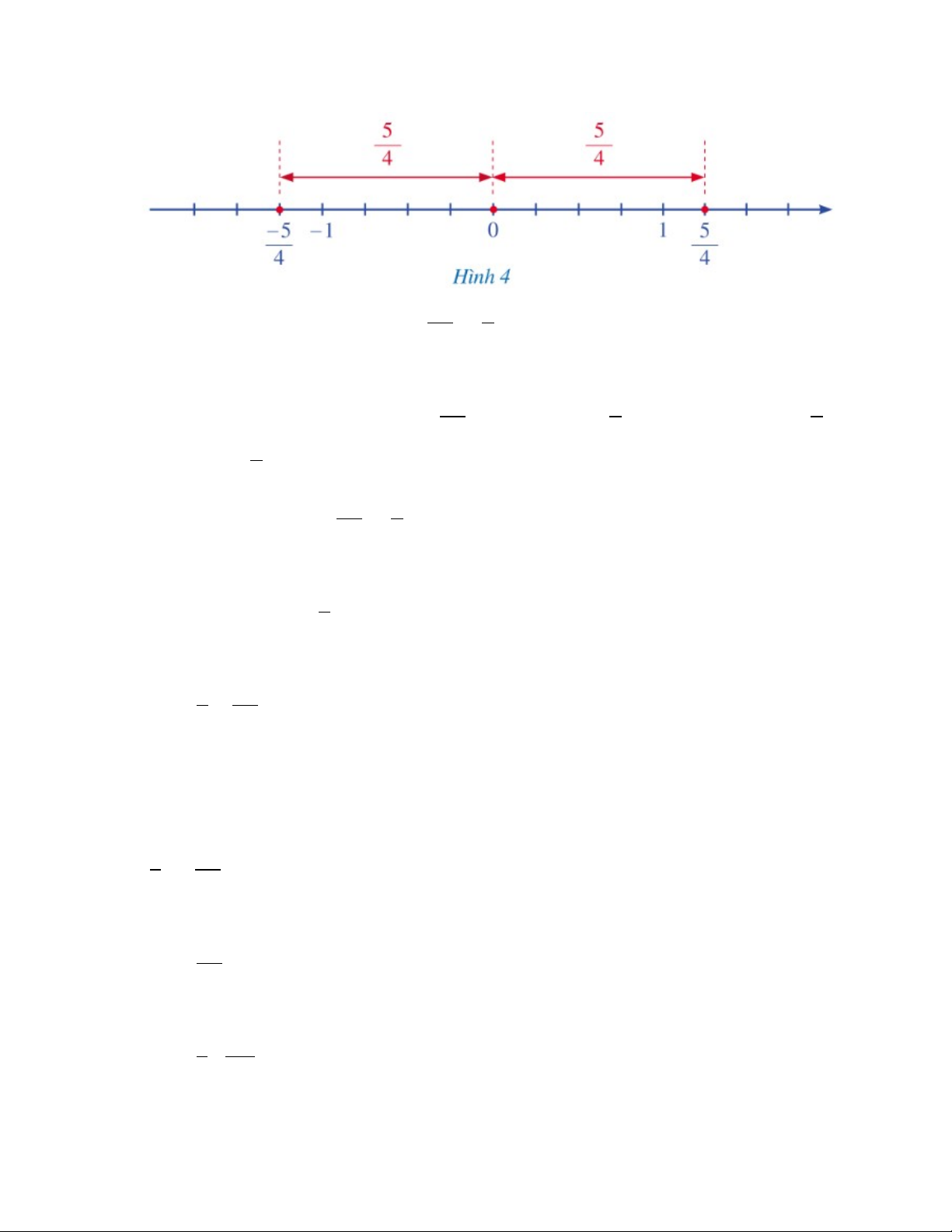
Quan sát hai điểm biểu diễn các số hữu tỉ
−5
4
và
5
4
trên trục số sau: (Hình 4)
Trang 3 | 15
Nêu nhận xét về khoảng cách từ hai điểm
−5
4
và
5
4
đến điểm gốc 0.
Lời giải:
Dựa vào hình vẽ trên, khoảng cách từ điểm
−5
4
đến điểm gốc 0 là
5
4
và khoảng cách từ điểm
5
4
đến điểm gốc 0 là
5
4
.
Vậy khoảng cách từ hai điểm
−5
4
và
5
4
đến điểm gốc 0 bằng nhau.
Câu 7:
Tìm số đối của mỗi số sau:
2
9; − 0,5
Lời giải:
Số đối của
2
9
là
−2
9
.
Số đối của − 0,5 là − (−0,5) = 0,5.
Câu 8:
So sánh:
a)
−1
3
và
−2
5
;
b) 0,125 và 0,13;
c) – 0,6 và
−2
3
.
Lời giải:
a) Ta có
−1
3=−1
3
.
Trang 4 | 15

Các số
−1
3
và
−2
5
là các phân số có mẫu số dương.
Thực hiện quy đồng mẫu các phân số, ta được:
−1
3=
(
−1
)
.5
3.5=−5
15
;
−2
5=
(
−2
)
.3
5.3=−6
15
.
Vì − 5 > − 6 nên
−5
15 >−6
15
hay
−1
3>−2
5
.
Vậy
−1
3>−2
5
.
b) Cách 1: Hai số 0,125 và 0,13 đều có phần số nguyên là 0.
Ta so sánh chữ số phần thập phân của hai số:
- Chữ số hàng phần mười của hai số đều là 1.
- Chữ số hàng phần trăm của số 0,125 là 2 và của số 0,13 là 3.
Vì 2 < 3 nên 0,125 < 0,13.
Vậy 0,125 < 0,13.
c) – 0,6 và
−2
3
.
Ta có
−0,6=−6
10 =−3
5
.
Thực hiện quy đồng mẫu số hai phân số, ta được:
−3
5=
(
−3
)
.3
5.3=−9
15 ;−2
3=
(
−2
)
.5
3.5=−10
15
Vì – 9 > – 10 nên
−9
15 >−10
15
hay
−0,6>−2
3
.
Vậy
−0,6>−2
3
.
Câu 9:
So sánh:
a) – 3,23 và – 3,32;
b)
−7
3
và – 1,25.
Lời giải:
Trang 5 | 15


























