Bài tập Tổng các góc trong một tam giác có đáp án
----------------------------------------
Câu 1:
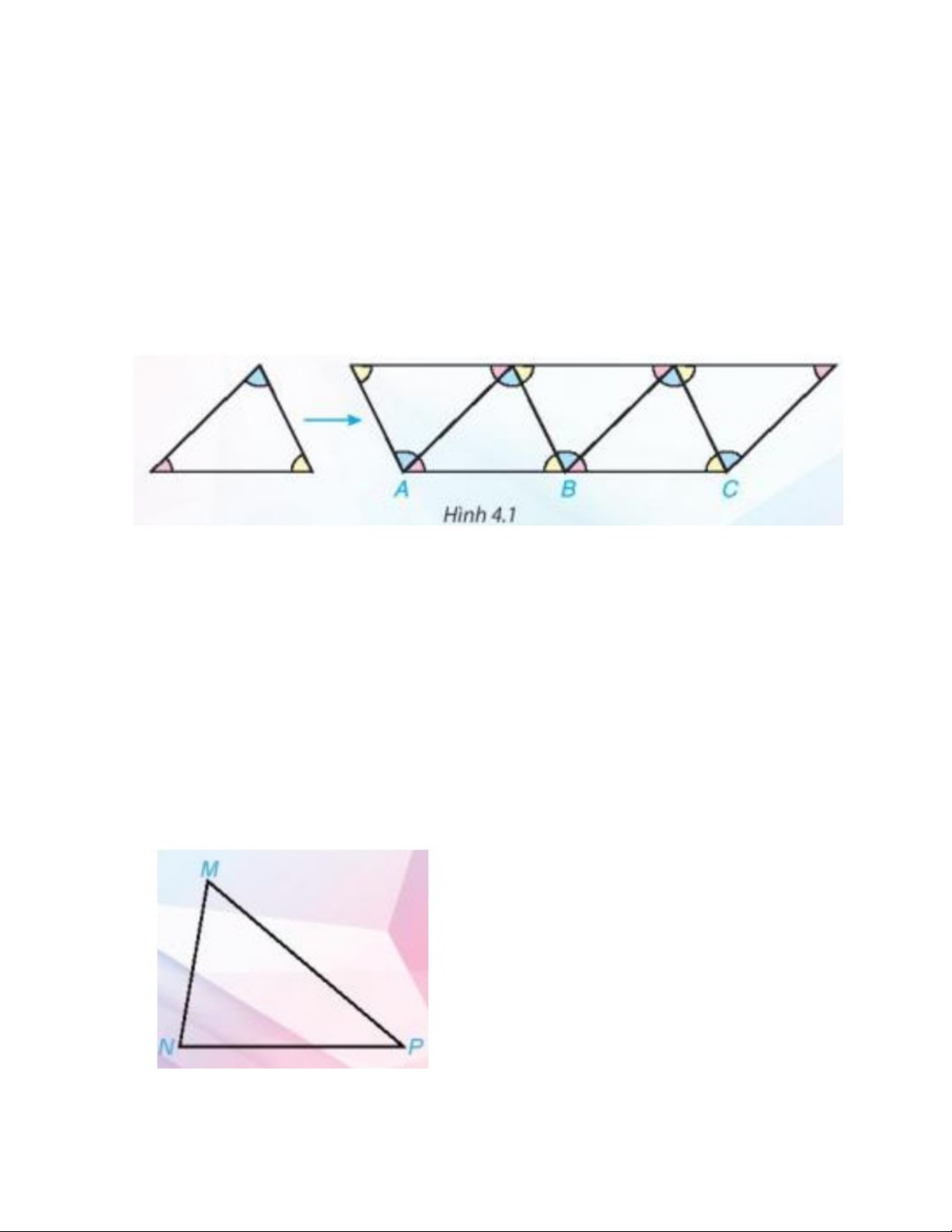
Người ta có thể xếp các viên gạch hình tam giác giống hệt nhau để trang trí như Hình 4.1. Em có
nhận xét gì về ba góc tại mỗi đỉnh chung của ba tam giác? Từ đó em rút ra kết luận gì về vị trí
của ba điểm A, B, C?
Lời giải:
Nhận xét: Khi xếp các viên gạch hình tam giác giống hệt nhau để trang trí như Hình 4.1 ta thấy
ba góc tại mỗi đỉnh chung của ba tam giác tạo thành một góc bẹt nên chúng có tổng số đo bằng
180°.
Kết luận: Ba điểm A, B, C thẳng hàng.
Câu 2:
Vẽ tam giác MNP bất kì, đo ba góc của tam giác đó.
- Tổng số đo ba góc của tam giác MNP bằng bao nhiêu?
- So sánh kết quả của em với các bạn và rút ra nhận xét.
Lời giải:
Trang 1 | 6
- Tổng số đo ba góc của tam giác MNP bằng
180❑∘.
- Nhận xét: Tổng số đo ba góc của một tam giác bằng
180❑∘.
Câu 3:
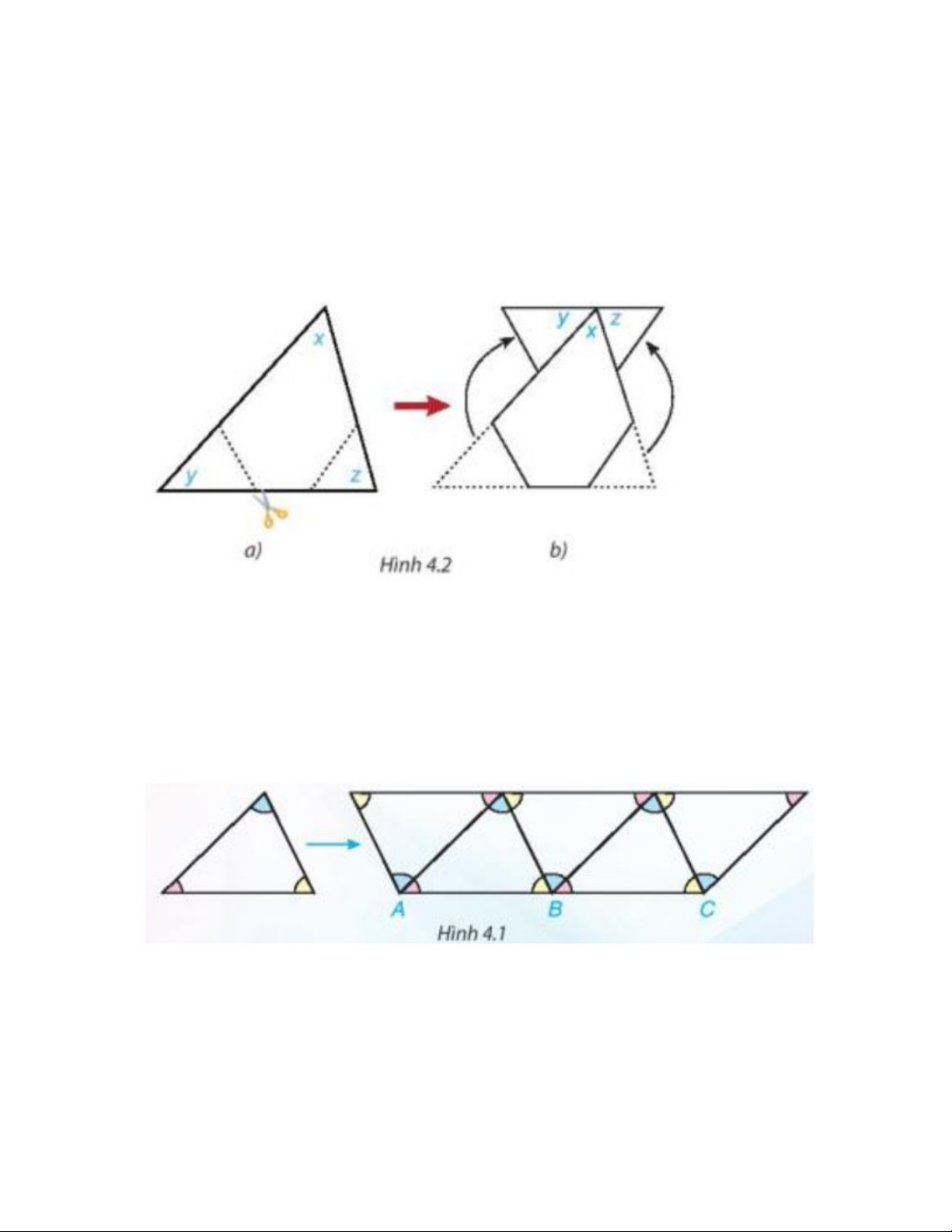
Cắt một hình tam giác bằng giấy bất kì (H.4.2a). Đánh dấu ba góc là x, y, z. Cắt hai góc y, z và
ghép lên góc x như Hình 4.2b. Từ đó em hãy dự đoán tổng số đo các góc x, y, z của tam giác ban
đầu.
Lời giải:
Dựa vào Hình 4.2b, dự đoán tổng số đo các góc x, y, z của tam giác ban đầu bằng
180❑∘
.
Câu 4:
Trở lại tình huống mở đầu, tổng ba góc tại mỗi đỉnh chung của ba tam giác (chẳng hạn tại B
trong Hình 4.1) bằng bao nhiêu độ? Ba điểm A, B, C có thẳng hàng không?
Lời giải:
Tổng ba góc tại mỗi đỉnh chung của ba tam giác bằng
180❑∘.
Ba điểm A, B, C thẳng hàng.
Câu 5:
Trang 2 | 6
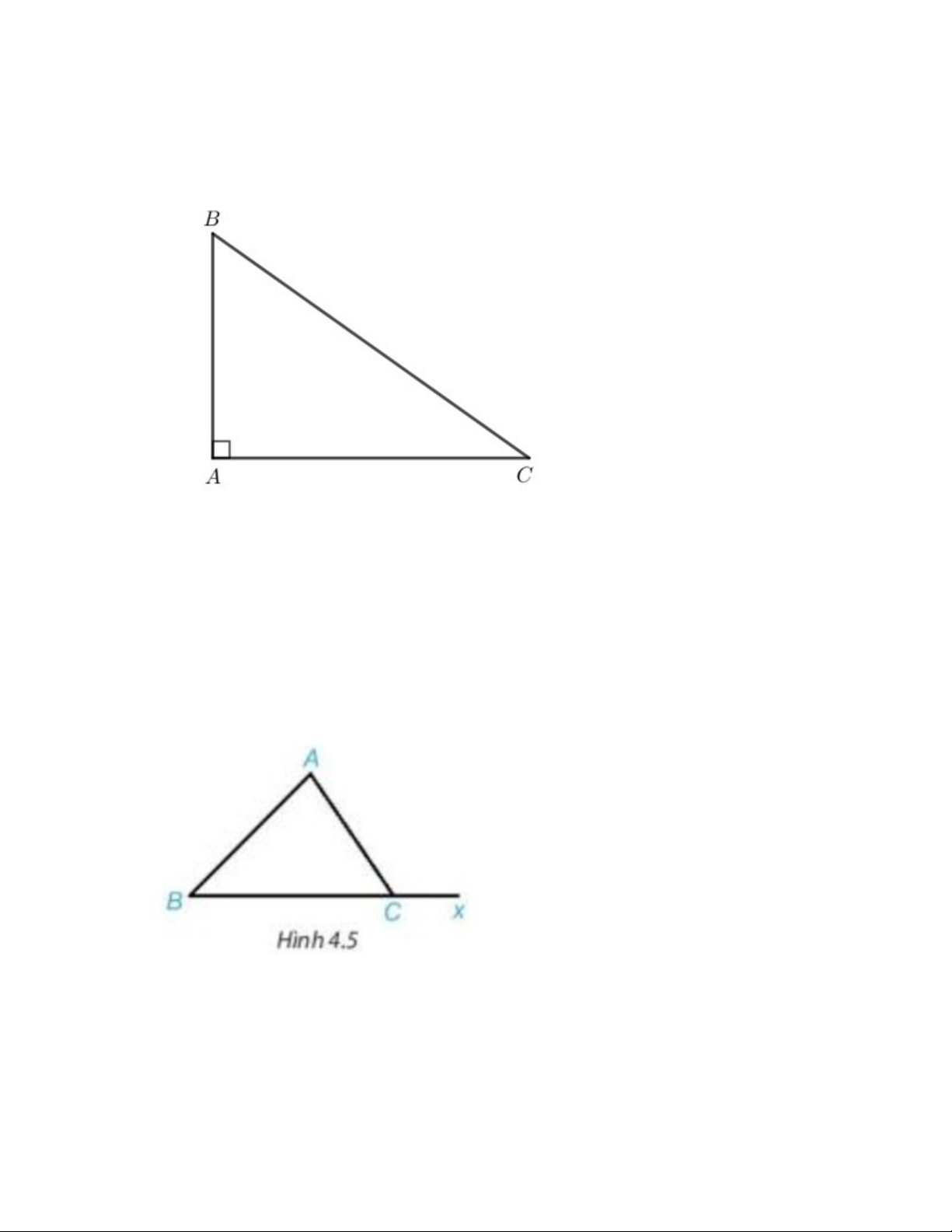
Cho tam giác ABC vuông tại A. Tính tổng hai góc B và C.
Lời giải:
Xét tam giác ABC có
^
A+
^
B+
^
C=180❑∘.
Do đó
^
B+
^
C=180❑∘−
^
A=180❑∘−90❑∘=90❑∘.
Vậy
^
B+
^
C=90❑∘.
Câu 6:
Cho tam giác ABC và Cx là tia đối của tia CB (H.4.5).
Chứng minh rằng
^
A C x=
^
B A C+
^
C B A .
Lời giải:
Do Cx là tia đối của tia CB nên
^
BC x=180❑∘.
hay
^
A C x+
^
A C B=180❑∘.
hay
^
A C x=180❑∘−
^
A C B
(
1
)
.
Trang 3 | 6
Xét tam giác ABC có
^
A C B+
^
B A C +
^
C B A=180❑∘.
hay
^
B A C +
^
C B A=180❑∘−
^
A C B
(
2
)
.
Từ (1) và (2) ta có
^
A C x=
^
B A C+
^
C B A .
Vậy
^
A C x=
^
B A C+
^
C B A .
Câu 7:
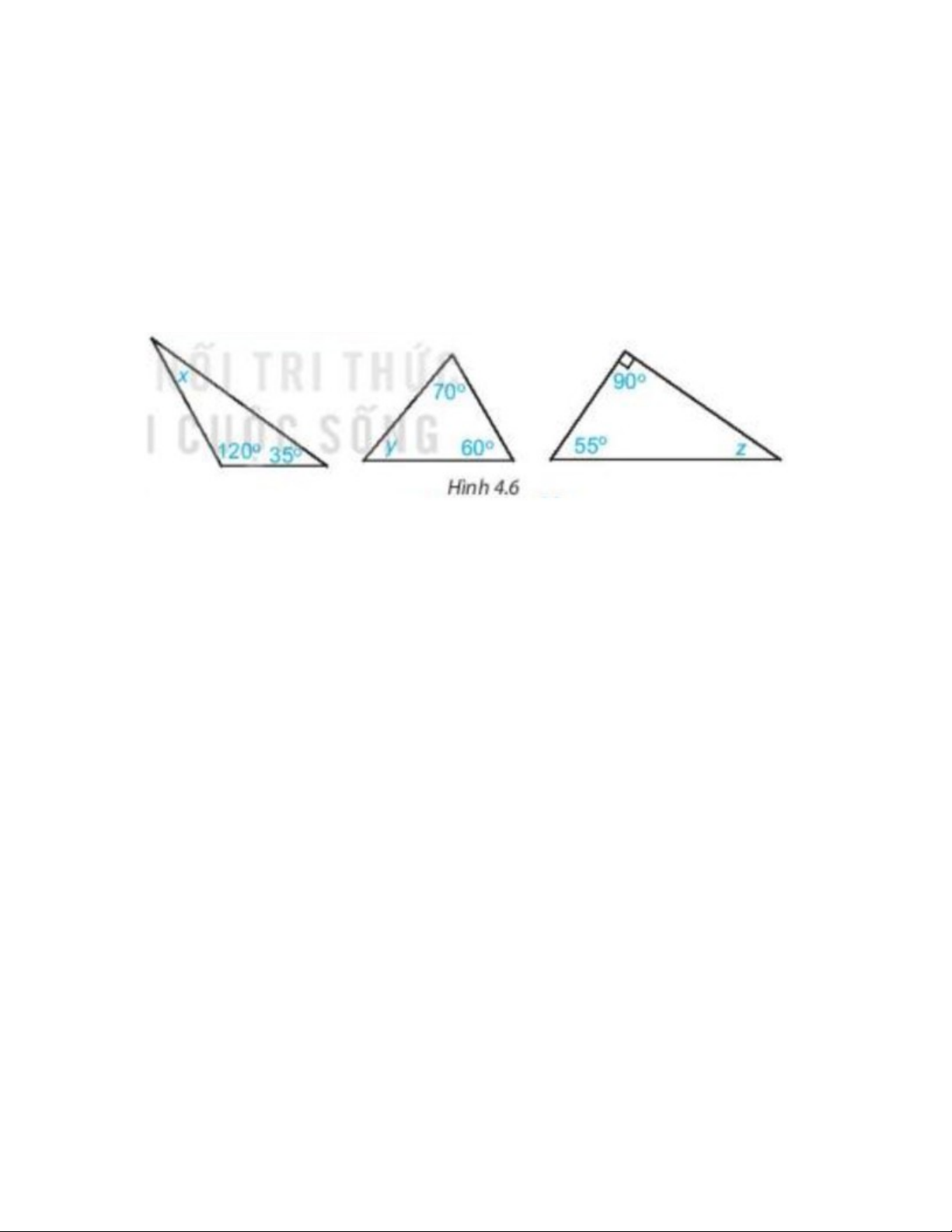
Tính số đo các góc x, y, z trong Hình 4.6.
Lời giải:
Xét tam giác trong hình đầu tiên có
x+120❑∘+35 ❑∘=180 ❑∘
Do đó
x=180❑∘−120❑∘−35 ❑∘=25 ❑∘.
Xét tam giác trong hình thứ hai có
y+70❑∘+60❑∘=180❑∘.
Do đó
y=180 ❑∘−70❑∘−60❑∘=50❑∘.
Xét tam giác trong hình thứ ba có
z+90❑∘+55❑∘=180❑∘.
Do đó
z=180❑∘−90❑∘−55❑∘=35❑∘.
Vậy
x=25❑∘; y=50❑∘; z=35 ❑∘.
Câu 8:
Trong các tam giác (H.4.7), tam giác nào là tam giác nhọn, tam giác vuông, tam giác tù?
Trang 4 | 6
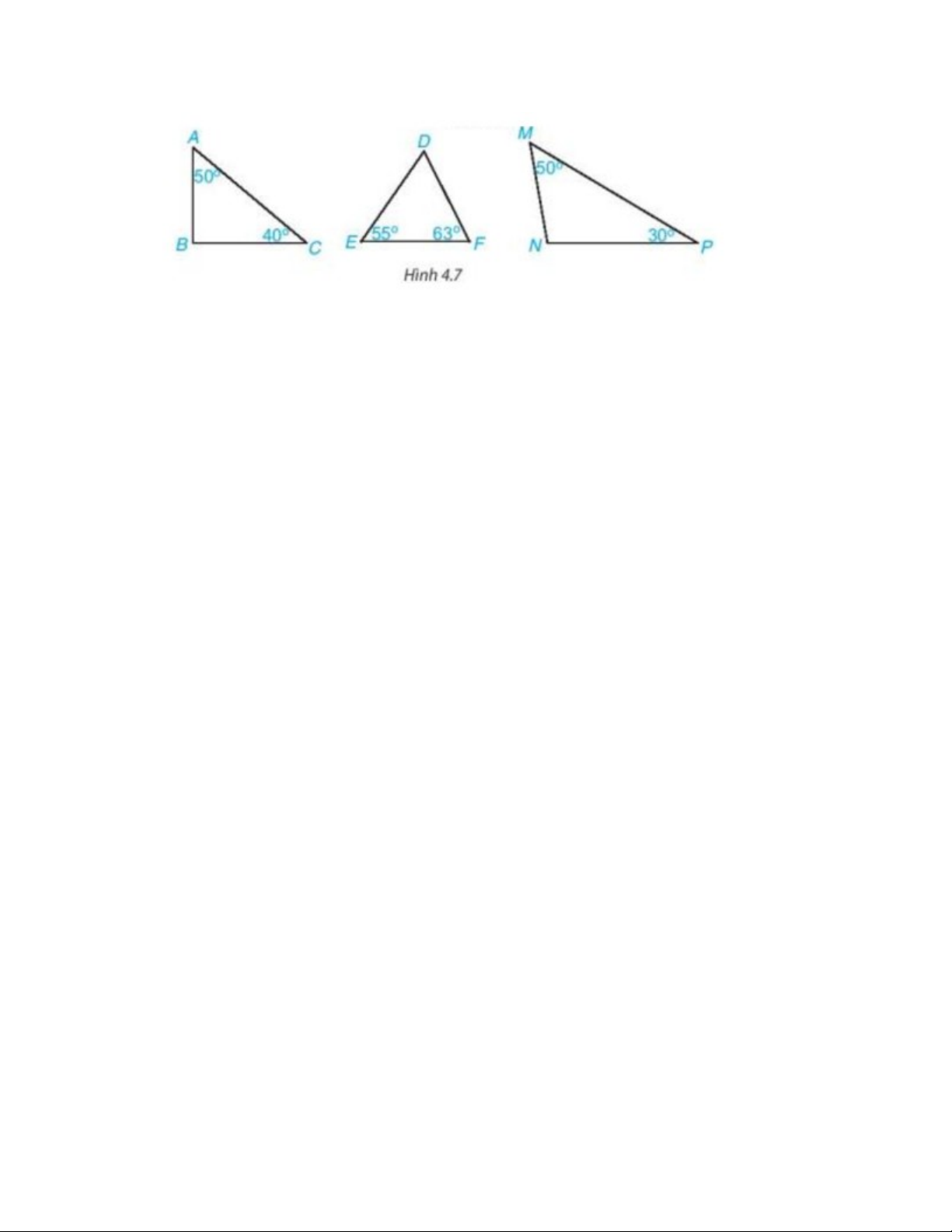
Lời giải:
Xét tam giác ABC có
^
A+
^
B+
^
C=180❑∘.
Do đó
^
B=180❑∘−
^
A −
^
C=180❑∘−50❑∘−40❑∘=90❑∘.
Do đó góc B là góc vuông.
Tam giác ABC có một góc vuông nên tam giác ABC là tam giác vuông.
Xét tam giác DEF có
^
D+
^
E+
^
F=180❑∘.
Do đó
^
D=180 ❑∘−
^
E −
^
F=180❑∘−55❑∘−63 ❑∘=62❑∘.
Do
62❑∘<90❑∘
nên góc D là góc nhọn.
Tam giác DEF có ba góc nhọn nên tam giác DEF là tam giác nhọn.
Xét tam giác MNP có
^
M+
^
N+
^
P=180❑∘.
Do đó
^
N=180 ❑∘−50❑∘−30❑∘=100❑∘.
Do
100❑∘>90❑∘
nên góc N là góc tù.
Tam giác MNP có một góc tù nên tam giác MNP là tam giác tù.
Vậy tam giác ABC là tam giác vuông, tam giác DEF là tam giác nhọn, tam giác MNP là tam giác
tù.
Câu 9:
Tính các số đo x, y, z trong Hình 4.8.
Trang 5 | 6


























