
Bài tập Số vô tỉ, Căn bậc hai số học có đáp án
----------------------------------------
Câu 1:
Viết số hữu tỉ
1
3
dưới dạng số thập phân vô hạn tuần hoàn.
Lời giải:
Ta thực hiện đặt phép tính chia 1 cho 3 như sau:
Sau khi thực hiện phép tính chia 1 cho 3 ta được kết quả là 0,3333….
Vậy số hữu tỉ
1
3
có thể viết dưới dạng số thập phân vô hạn tuần hoàn là 0, 3333… = 0, (3)
Câu 2:
Khẳng định “Mỗi số vô tỉ đều không thể là số hữu tỉ” là đúng hay sai? Vì sao?
Lời giải:
Khẳng định trên là đúng vì mỗi số vô tỉ đều được viết dưới dạng số thập phân vô hạn không tuần
hoàn, còn các số hữu tỉ thì được viết dưới dạng các số thập phân hữu hạn hoặc vô hạn tuần hoàn.
Do vậy nếu một số là vô tỉ thì số đó không thể là số hữu tỉ.
Câu 3:
Tính
Trang 1 | 5

a) 32
b) (0,4)2
Lời giải:
a) 32 = 3.3 = 9
b) (0,4)2 = 0,4.0,4 = 0, 16
Câu 4:
Tính giá trị của:
a
)
√
1600 ;b
)
√
0,16 ;c
)
√
21
4.
Lời giải:
Ta có:
a
)
√
1600=
√
402=40 b
)
√
0,16=
√
0,42=0,4c
)
√
21
4=
√
9
4=
√
(
3
2
)
2
=3
2
Câu 5:
Ta có thể tính được giá trị (đúng hoặc gần đúng) căn bậc hai số học của một số dương bằng máy
tính cầm tay. Chẳng hạn, để tính
√
3;
√
256.36
, ta sử dụng nút dấu căn bậc hai số học
√
❑
và làm
như sau:
Lời giải:
Học sinh làm theo hướng dẫn của đề bài.
Câu 6:
a) Đọc các số sau:
√
15 ;
√
27 ,6;
√
0,82
b) Viết các số sau: Căn bậc hai số học của 39; căn bậc hai số học của
9
11
; căn bậc hai số học của
89
27
.
Lời giải:
Trang 2 | 5
a) Đọc số:
√
15 : C ă n b ậ c h a i s ố h ọ c c ủ a 15 .
√
27 ,6 : C ă n b ậ c h a i s ố h ọ c c ủ a 27 ,6.
√
0,82 : C ă n b ậ c h a i s ố h ọ c c ủ a 0,82 .
b
)
C ă nb ậ c ha i s ố h ọ c c ủa 39l à
√
39C ă n b ậ c h a i s ố h ọ c c ủ a 9
11 l à
√
9
11 .C ă n b ậ c h a i s ố h ọ c c ủ a 89
27 l à
√
89
27 .
Câu 7:
Chứng tỏ rằng:
a) Số 0,8 là căn bậc hai số học của 0,64;
b) Số –11 không phải căn bậc hai số học của 121.
c) Số 1,4 là căn bậc hai số học của 1,96 nhưng –1,4 không phải căn bậc hai số học của 1,96.
Lời giải:
a) Ta có: (0,8)2 = 0,8.0,8 = 0,64 và 0,8 > 0 nên 0,8 là căn bậc hai số học của 0,64.
b) Ta có: (–11)2 = (–11).(–11) = 121 nhưng –11 < 0 nên –11 không là căn bậc hai số học của
121.
c) Ta có: (1,4)2 = 1,4.1,4 = 1,96 và 1,4 > 0 nên 1,4 là căn bậc hai số học của 1,96.
(–1,4)2 = (–1,4).(–1,4) = 1,96 nhưng –1,4 < 0 nên –1,4 không là căn bậc hai số học của 1,96.
Câu 8:
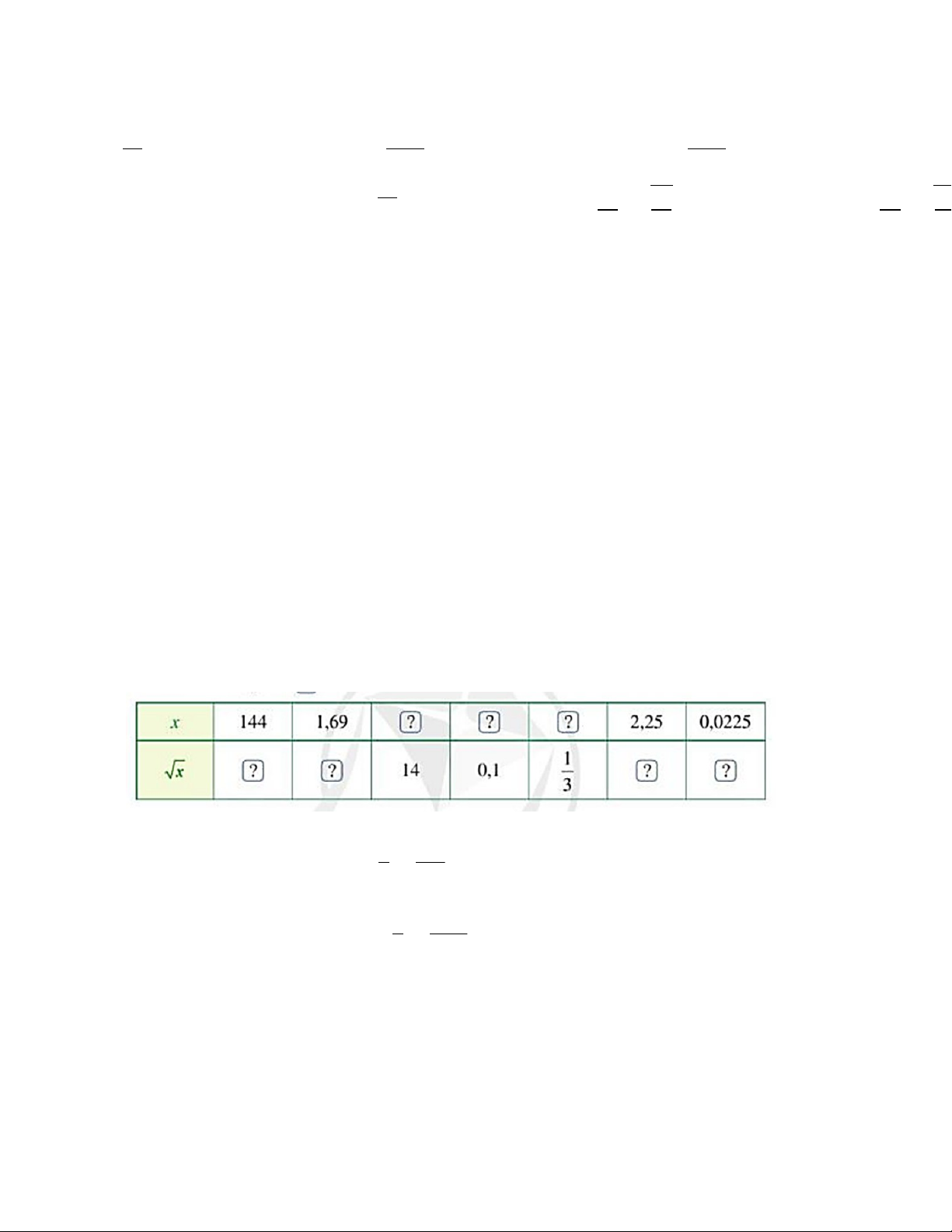
Tìm số thích hợp cho
?
:
Lời giải:
+) Ta có: 144 = 122 và 12 > 0 nên
√
x=
√
144
=12.
Khi đó
?
điền số 12.
+) Ta có: 1,69 = 1,32 và 1,3 > 0 nên
√
x=
√
1,69
= 1,3.
Khi đó
?
điền số 1,3.
+) Ta có: 142 = 14.14 = 196 nên x = 196.
Khi đó
?
điền số 196.
+) Ta có: 0,12 = 0,1.0,1 = 0,01 nên x = 0,01.
Trang 3 | 5
Khi đó
?
điền số 0,01.
+) Ta có: nên x =
1
9
.
Khi đó
?
điền số
√
x=
√
2,25=1,5
.
+) Ta có: 2,25 = 1,52 và 1,5 > 0 nên
√
x=
√
0,0225=0,15
.
Khi đó
?
điền số 1,5.
+) Ta có: 0,0225 = 0,152 và 0,15 > 0 nên .
Khi đó
?
điền số 0,15.
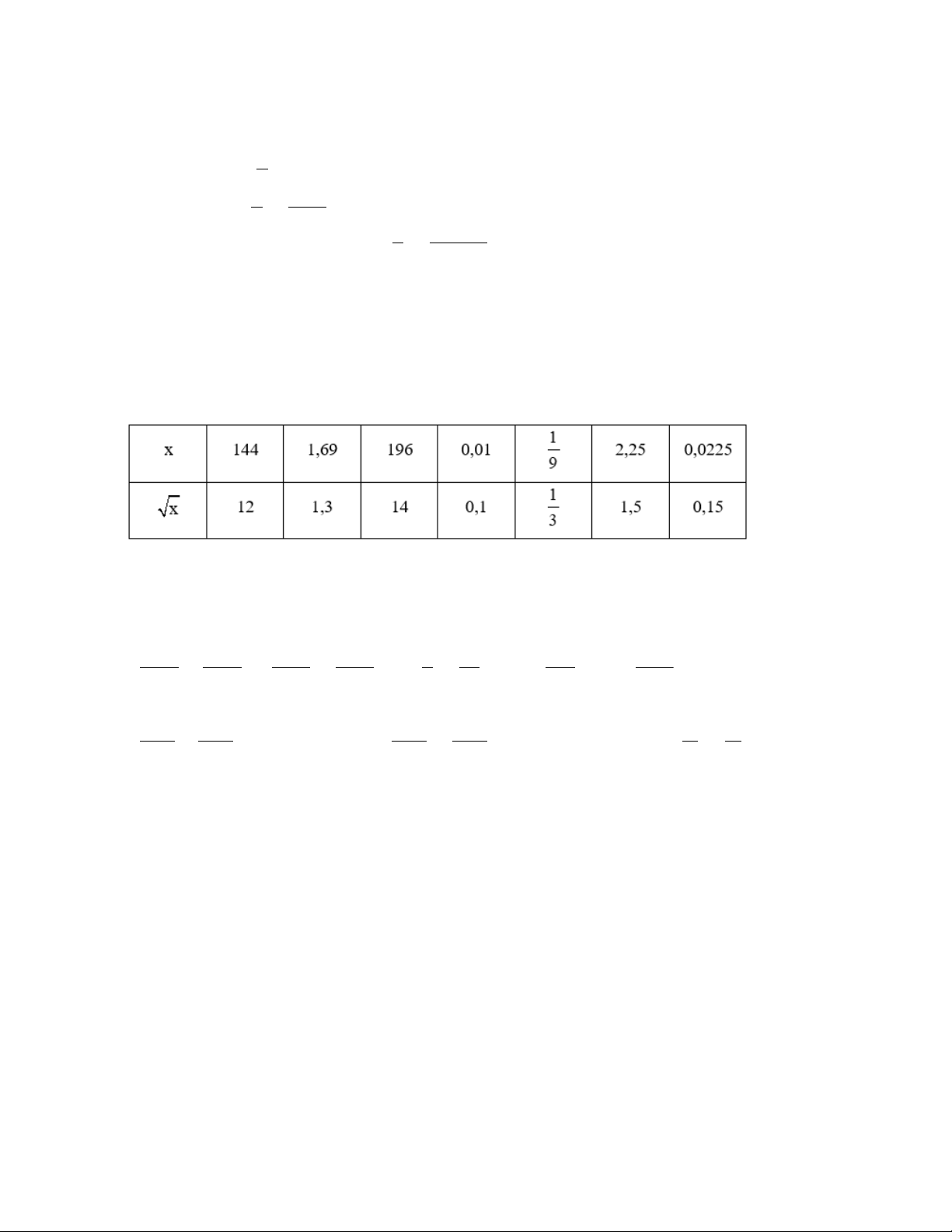
Ta có bảng sau:
Câu 9:
Tính giá trị của biểu thức:
a
)
√
0,49+
√
0,64 b
)
√
0,36 −
√
0,81 c
)
8.
√
9−
√
64 d
)
0,1.
√
400+0,2.
√
1600
Lời giải:
a
)
√
0,72+
√
0,82=0,7+0,8=1,5b
)
√
0,62−
√
0,92=0,6−0,9=−0,3c
)
8.
√
32−
√
82=8.3−8=24 −8=16 d
)
0,1.
√
202+0,2.
√
402=0,1.20+0,2.40=2+8=10
Câu 10:
Quan sát Hình 1, ở đó hình vuông AEBF có cạnh bằng 1 m, hình vuông ABCD có cạnh AB là
một đường chéo của hình vuông AEBF.
a) Tình diện tích của hình vuông ABCD.
b) Tính độ dài đường chéo AB.
Trang 4 | 5
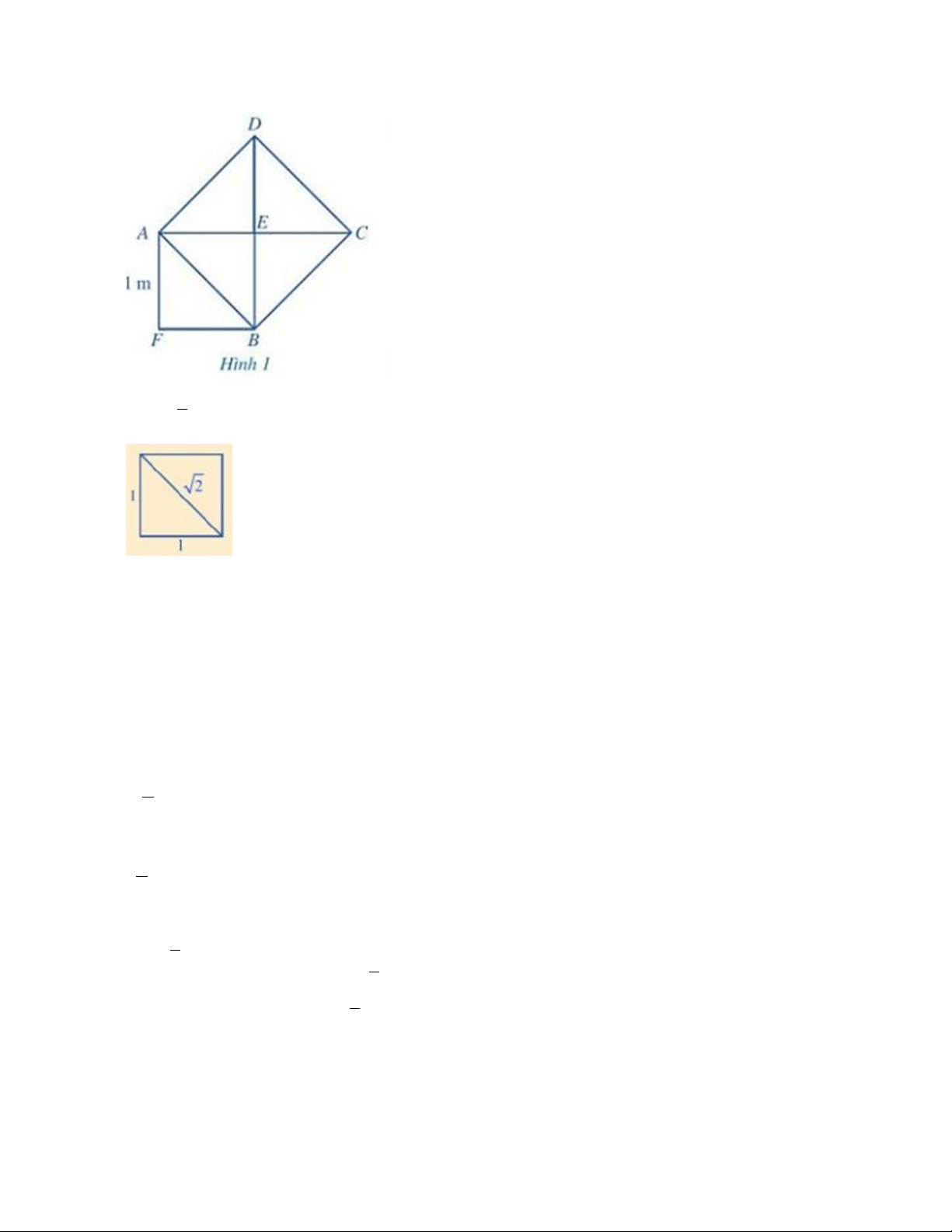
Lưu ý:
√
2
là độ dài đường chéo của hình vuông có cạnh bằng 1.
Lời giải:
a) Quan sát Hình 1 ta thấy hình vuông ABCD được tạo thành từ 4 tam giác nhỏ bằng nhau nên
diện tích hình vuông ABCD gấp 4 lần diện tích tam giác AEB.
Hình vuông AEBF là hình vuông có cạnh bằng 1 và tạo bởi hai tam giác là AEB và AFB nên
diện tích của hình vuông AEBF gấp 2 lần diện tích của tam giác AEB.
Diện tích hình vuông AEBF có cạnh bằng 1 m là: 1.1 = 1 (m2).
Diện tích hình vuông AEBF gấp 2 lần diện tích tam giác AEB nên diện tích tam giác AEB là: 1 :
2 =
1
2
(m2).
Diện tích hình vuông ABCD gấp 4 lần diện tích tam giác AEB nên diện tích hình vuông ABCD
là:
1
2
.4 = 2 (m2).
Vậy diện tích hình vuông ABCD là 2 m2.
b) Do
√
2
là độ dài đường chéo của hình vuông có cạnh bằng 1, mà hình vuông AEBF có cạnh
bằng 1 m nên đường chéo AB là
√
2
m.
Vậy độ dài đường chéo AB là
√
2
m.
Trang 5 | 5


























