Giáo trình lập trình nâng cao - Chương 5

Chia sẻ: Nguyễn Nhi | Ngày: | Loại File: PDF | Số trang:10

Thêm vào BST

Báo xấu

131
lượt xem 33
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Tài liệu tham khảo Giáo trình lập trình nâng cao trên ngôn ngữ Pascal soạn theo chương trình đã được Bộ giáo dục và đào tạo phê chuẩn - Chương 5 Giải thuật đệ quy

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Giáo trình lập trình nâng cao - Chương 5

Chương 5 Gi i thu t ñ quy N i dung c a chương này ñ c p ñ n nh ng bài toán có tính ñ quy. Không ph i bài toán nào cũng có tính ñ quy và không ph i các bài toán có tính ñ quy thì ñ u ph i gi i b ng gi i thu t ñ quy. Các v n ñ c n quan tâm trong chương này: Bài toán có tính ñ quy không Có c n dùng gi i thu t ñ quy không ð quy có mang l i hi u qu hơn các phương pháp thông thư ng hay không Trư ng ð i h c Nông nghi p 1 - Giáo trình L p trình nâng cao ..............................................................- 133
1. Khái ni m ñ quy Trong thân m t chương trình con có th ñưa l i g i t i chính chương trình con ñó, tính ch t này ñư c g i là tính "ð qui c a chương trình con". Trong toán h c khái ni m giai th a ñư c ñ nh nghĩa như sau: 0! = 1 N u n > 0 thì n! = 1*2*3*...*n T ñ nh nghĩa trên d dàng th y r ng n! = n*(n-1)! (n-1)! = (n-1)*(n-2)! ...... 1! = 1*0! =1 Cách th c l p lu n như trên ñưa chúng ta t i m t nh n xét t ng quát là: l i gi i c a bài toán A có th ñư c th c hi n b i l i gi i c a bài toán A' có d ng gi ng như A. Th t v y, vi c tính n! có th ñư c th c hi n b i vi c tính (n-1)!. ði u quan tr ng ñ bài toán có l i gi i là tuy A' gi ng như A song th c ch t A' ph i nh hơn A và quá trình "thu nh " ph i có ñi m d ng. Trong bài toán tính giai th a t ch c n tính giai th a c a n chúng ta ñi tính giai th a c a (n-1), ñ tính giai th a c a (n-1) chúng ta ñi tính giai th a c a (n-2)... k t thúc là giai th a c a 0. M t ñ i tư ng ñư c g i là ñ quy n u nó ñư c ñ nh nghĩa dư i d ng c a chính nó. Gi i thu t c a bài toán A ñư c g i là ñ quy n u nó d n t i vi c gi i bài toán A' gi ng như A nhưng nh hơn A và quá trình ph i có ñi m d ng. Xét bài toán tính giai th a v i n = 5: Ô nh cu i 1! = 1 5! = 5*4! 2! = 2*1! 4! = 4*3! 3! = 3*2! 3! = 3*2! 4! = 4*3! 2! = 2*1! Ô nh ñ u 5! = 5*4! 1! = 1 Hình 5.1 Như v y khi bi t 1! thì tính ñư c 2!, bi t 2! Thì tính ñư c 3!,... B ng cách s d ng b nh ngăn x p theo nguyên t c LIFO ( Last In - First Out) (Hình 1.3) nh ng gì g i vào cu i cùng thì ñư c l y ra trư c tiên. Bóc ô nh trên ñ nh ta có 1! = 1 và l ra ô ti p theo 2! = 2*1!. Vì 1! ñã bi t nên tính ñư c 2! = 2, bóc ti p ô nh phía dư i ta có 3! = 3*2!, vì 2! ñã bi t nên 3! = 3*2 = 6 quá trình ti p t c cho ñ n khi bóc ô nh dư i cùng và chúng ta nh n ñư c 5! = 120. Dư i ñây là chương trình tính giai th a Trư ng ð i h c Nông nghi p 1 - Giáo trình L p trình nâng cao ..............................................................- 134
Ví d 5.1: Program Giaithua; Uses crt; Var n: integer; Function GT(m: integr): integer; (* Hàm GT tính giai th a c a n*) Begin if m=0 then GT:=1 else GT:= m*GT(m-1); (*G i ñ qui c a GT *) End; Begin Clrscr; write ('Tinh giai thua cua n = '); Readln (n) (*ð c giá tr n*) write('Gia thua cua ',n, ' = ',GT(n)); (* Vi t giá tr hàm GT *) Repeat until keypressed; End. Ví d 5.1 có m t s ñi u ñáng lưu ý sau ñây: 1. Hàm GT ñư c xây d ng ñ tính giai th a v i tham s hình th c m, ki u c a m là ki u Integer. Giá tr m sau này s ñư c thay th b ng tham s th c n qua l i g i GT(n) trong chương trình m . 2. Khi ñ nh nghĩa ki u c a GT là Integer thì giá tr c a n ch ñư c ch n nh hơn 8 vì 8! = 40320 vư t quá giá tr c c ñ i c a Integer (32767). ð có th tính giai th a v i n>=8 ta ph i ñ nh nghĩa function GT có ki u Longint ho c Real. V i ki u Real l nh vi t giá tr c a giai th a ph i là vi t s th c v i ph n l b ng 0, ví d : Write (GT(n):12:0); 3. S d ng thu t toán ñ quy ñ ng nghĩa v i vi c ph i xây d ng chương trình con, vì v y n u s d ng các vòng l p có th gi i ñư c bài toán thì nên dùng vòng l p. Tr trư ng h p b t bu c ph i gi i bài toán không có tính l p ho c bài toán có kh năng truy h i. V i bài toán tính giai th a có th dùng vòng l p và chúng ta th y chương trình s ñơn gi n hơn nhi u so v i cách dùng tính ñ quy: Ví d 5.2 Program Tinh_GT; Uses crt; Var i,n:byte; gt:longint; Begin Clrscr; Write(' Nhap gia tri n '); Readln(n); if (n = 0) or (n=1) then gt:=1; if n > 1 then gt:=1; For i:= 1 to n do gt:=gt*i; Writeln('Giai thua cua ',n,' = ',gt); Trư ng ð i h c Nông nghi p 1 - Giáo trình L p trình nâng cao ..............................................................- 135
Readln; End. Ví d 5.3: L p chương trình tìm ư c s chung l n nh t c a hai s nguyên n, m. Ư c s chung l n nh t c a hai s n và m tính theo công th c : nn um=0 USC(n,m) = USC(m, n mod m ) n u m 0 Ví d n= 4, m=8 USC(4,8) = USC(8, 4) = USC(4,0) = 4 Chương trình ñư c xây d ng như sau: Program timUSC ; Uses crt; Var n,m : word; Lam: Char; FUNCTION USC(a,b:word): word; Begin If b=0 then USC := a Else USC := USC(b,a mod b); End; BEGIN Repeat Clrscr; Write(' Hay cho hai so "n" va "m" can tim uoc so chung '); Readln(n,m); Writeln(' Uoc so chung lon nhat cua ',n,' va ',m, ' la ',USC(n,m):5); Writeln; Write('Tim tiep hay thoi ? C/K '); read(lam); Until Upcase(lam)='K'; END. 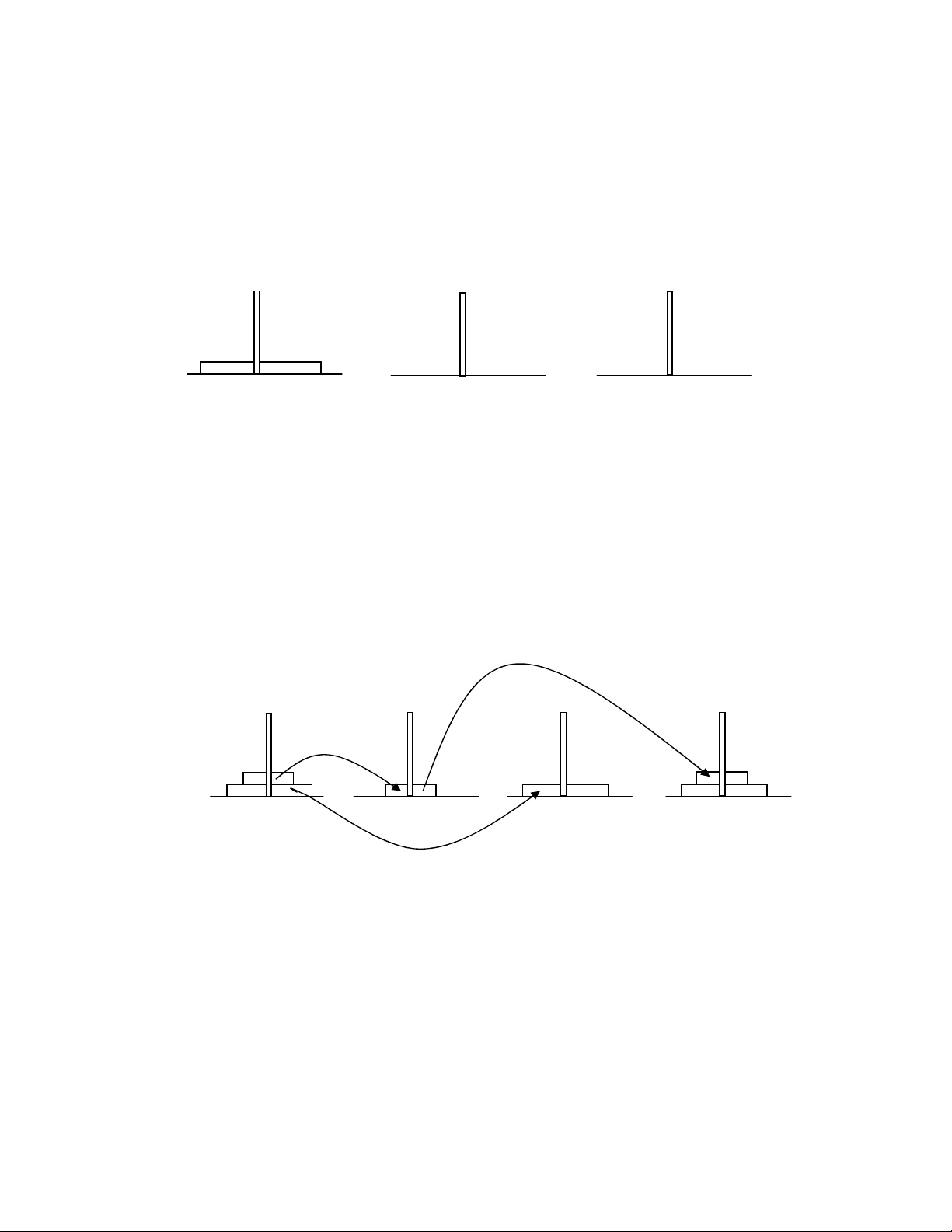Bài toán kinh ñi n ng d ng gi i thu t ñ quy là bài toán Tháp Hanoi. N i dung bài toán như sau: Có n chi c ñĩa tròn ñư ng kính khác nhau, các ñĩa có l gi a. Ngư i ta x p l ng các ñĩa này vào m t c c theo th t trên nh dư i to. Yêu c u ph i x p các ñĩa này sang c c m i theo nguyên t c: 1. M i l n ch ñư c chuy n 1 ñĩa 2. Không ñư c ñ x y ra tình tr ng ñĩa to trên, ñĩa nh dư i dù là t m th i 3. ðư c phép dùng m t c c trung gian Trư ng ð i h c Nông nghi p 1 - Giáo trình L p trình nâng cao ..............................................................- 136
Gi s c c ñ u tiên là c c A, c c trung gian là B và c c c n x p ñĩa sang là c c C. Chúng ta s xét m t s trư ng h p ñơn gi n ñ tìm quy lu t (Hình 5.2) * n =1: c c A ch có m t ñĩa Chuy n ñĩa t c c A sang c c C K t thúc A B C Hình 5.2 * n = 2: c c A có 2 ñĩa (Hình 5.3) Chuy n ñĩa trên sang B Chuy n ñĩa dư i sang C Chuy n ñĩa t B sang C K t thúc A B C C Hình 5.3 * n = 3: c c A có 3 ñĩa V i trư ng h p 3 ñĩa n u chúng ta coi 2 ñĩa trên là m t ñĩa thì bài toán quy v trư ng h p n = 2, khi ñó l i gi i s là: (Hình 5.4) Chuy n 2 ñĩa trên sang B Chuy n ñĩa dư i cùng sang C Chuy n 2 ñĩa t B sang C K t thúc Trư ng ð i h c Nông nghi p 1 - Giáo trình L p trình nâng cao ..............................................................- 137
A B C Hình 5.4 Vi c chuy n 2 ñĩa t A sang B chúng ta ñã có l i gi i ( trư ng h p n = 2 ) Tóm l i v i bài toán n ñĩa chúng ta có l i gi i t ng quát là: - Chuy n n-1 ñĩa trên cùng t A sang B - Chuy n ñĩa dư i cùng t A sang C - Chuy n n-1 ñĩa t B sang C - K t thúc Vi c chuy n n-1 ñĩa t A sang B l i d n t i bài toán gi ng như chuy n n ñĩa, song s lư ng ñĩa ñã gi m ñi 1, nghĩa là: - Chuy n n-2 ñĩa t A sang B - Chuy n ñĩa th n-1 t A sang C - Chuy n n-2 ñĩa t B sang C - K t thúc Quá trình s d n t i lúc trên c c A ch còn ñĩa th n trên c c B có n-1 ñĩa và trên c c C không có ñĩa nào, ñ n ñây ta chuy n ñĩa th n t A sang C. Bài toán s ñươc thu nh l i v i vi c chuy n n-2 ñĩa t B sang A. S l n th c hi n các bư c chuy n v i n = 3 ñư c cho trong b ng 5.1, ñây chúng ta ñã quy ư c ñĩa trên cùng là ñĩa s 1, ñĩa gi a là ñĩa s 2 và ñĩa dư i cùng là ñĩa s 3. Dãy s trong các c c luôn luôn s p x p theo chi u tăng d n ch ng t r ng ñĩa nh luôn trên, ñĩa to luôn dư i. Trư ng ð i h c Nông nghi p 1 - Giáo trình L p trình nâng cao ..............................................................- 138
B ng 5.1 Bư c ý nghĩa C cA C cB C cC 0 1,2,3 1 Chuy n hai ñĩa trên cùng t A 2,3 1 sang B 2 3 2 1 3 3 1,2 4 Chuy n ñĩa s 3 t A sang C 1,2 3 5 Chuy n 2 ñĩa t B sang C 1 2 3 6 1 2,3 7 1,2,3 Các ví d trên cho th y s l n chuy n tăng r t nhanh khi s ñĩa tăng tuy n tính, v i n= 1 s l n chuy n là 1, v i n = 2 s l n chuy n là 3, v i n = 3 s l n chuy n là 7. B ng 5.2 Bư c ý nghĩa C cA C cB C cC 0 1,2,3,4 1 2,3,4 1 2 3,4 1 2 Chuy n 3 ñĩa trên cùng t c c 3,4 3 1,2 A sang c c trung gian B 4 4 3 1,2 5 1,4 3 2 6 1,4 2,3 7 4 1,2,3 8 Chuy n ñĩa 4 t A sang C 1,2,3 4 9 2,3 1,4 Chuy n 2 ñĩa trên cùng t B 2 10 3 1,4 sang A 11 1,2 3 4 12 Chuy n ñĩa 3 t B sang C 1,2 3,4 13 Chuy n 2 ñĩa 1 và 2 t A 2 1 3,4 sang C 14 1 2,3,4 15 1,2,3,4 Có th d dàng tìm ra công th c truy h i ñ tính s l n chuy n ñĩa N u s ñĩa là n thì s l n chuy n là 2n - 1 V i n = 4 s l n chuy n s là 15 (b ng 5.2). N u trên c c có 32 ñĩa thì s l n chuy n ñã là hơn 4 t , còn n u s ñĩa là 64 theo như bài toán c v tháp Hanoi thì s l n chuy n s là: 36893488147000000000 l n Trư ng ð i h c Nông nghi p 1 - Giáo trình L p trình nâng cao ..............................................................- 139
Gi s chúng ta cho r ng m i l n chuy n m t ñĩa h t 1 giây thì ñ chuy n h t s ñĩa nói trên t c c A sang c c C chúng ta c n 1 169 884 834 700 năm. ðây là kho ng th i gian mà b n thân h m t tr i và d i ngân hà cũng khó có th t n t i. 2. Thi t k gi i thu t ñ quy - Kh ñ quy V i m t bài toán toán b t kỳ, ñ xem nó có tính ñ quy hay không chúng ta ph i tr l i ñư c các câu h i sau ñây: 2.1 Bài toán ñã cho có th ñư c ñ nh nghĩa dư i m t d ng gi ng h t như nó nhưng có kích thư c nh hơn hay không? 2.2 Quá trình thu nh bài toán có d n t i m t ñi m d ng nào ñó hay không? Nói cách khác bài toán thu nh có d n t i m t trư ng h p ñ c bi t mà ta g i là trư ng h p xuy bi n nghiã là bi t l i gi i hay không? V i bài toán giai th a trư ng h p xuy bi n là 0! = 1 V i bài toán Tháp Hanoi trư ng h p xuy bi n là khi ch có 1 ñĩa trên c c A. 2.3 Khi x d ng tính ñ quy m i l n thu nh bài toán kích thư c bài toán gi m ñi như th nào? Các ví d v ñ quy có th xem trong nhi u tài li u v l p trình, v n ñ chúng ta quan tâm ñây là khi m t bài toán có th gi i quy t b ng c ñ quy và cách thông thư ng thì nên dùng cách nào? V i bài toán tính giai th a s d ng vòng l p For... vi c l p trình r t ñơn gi n, còn dùng ñ quy s ph c t p hơn. V i bài toán tìm ư c s chung l n nh t rõ ràng là cách dùng ñ quy s ñơn gi n hơn các cách khác. V i bài toán Tháp Hanoi n u không dùng ñ quy chúng ta khó mà tìm ra m t thu t gi i nào trong sáng hơn. Nói như v y cũng có nghĩa là không có m t chu n m c nào chung cho m i bài toán. Kinh nghi m c a các nhà l p trình ñã ch ra r ng n u m t bài toán v a có th gi i b ng ñ quy, v a có th gi i b ng phương pháp l p thông thư ng thì nên tránh dùng ñ quy. M t bài toán có th thay th gi i thu t ñ quy b ng các gi i thu t không t g i ñ n chúng thì g i là kh ñ quy. Ví d v i bài toán tính giai th a chúng ta hoàn toàn có th gi i b ng cách dùng vòng l p For . Bài toán trong trư ng h p này ñơn gi n hơn c v thu t toán l n k thu t l p trình. 3. Hi u l c c a bài toán ñ quy Như ñã nêu ñ quy là m t trong các công c ñ l p trình gi i các bài toán. C n kh ng ñ nh r ng ñ quy ch ñư c dùng cho m t s bài toán mà chúng ta tìm ñư c gi i thu t ñ quy. Tr l i ví d 4.16 v xây d ng cây nh phân. N u cây mà m i nút cha có nhi u nh t hai nút con nhưng không quy ñ nh rõ con bên trái và con bên ph i b trí th nào thì chúng ta không th dùng ñư c tính ñ quy. Trong trư ng h p quy ñ nh rõ giá tr con bên trái luôn nh hơn giá tr nút cha còn con bên ph i là l n hơn nút cha thì chúng ta th y vi c kh o sát m t cây nh phân t ng quát có th xuy v vi c kh o sát riêng t ng cây con bên trái và cây con bên ph i. Chương trình con Taocay trong ví d 4.16 ñã s d ng tính ñ quy ñ b xung d li u vào các nút, v i cách vi t này chương trình Taocay không ñơn gi n hơn cách vi t dùng vòng l p. Tuy nhiên khi duy t cây v i các chương trình con Quet_trung_tam, Quet_truoc, Quet_sau Trư ng ð i h c Nông nghi p 1 - Giáo trình L p trình nâng cao ..............................................................- 140
thì tính ñ quy ñã làm cho chương trình tr nên trong sáng và r t d hình dung là cây ñư c quét như th nao. Tính ñ quy v m t khía c nh nào ñó có th xem như tính quy n p toán h c, tuy nhiên c n phân bi t r ng ñ quy ñư c th c hi n là nh các b nh ki u LIFO ho c FIFO còn quy n p toán h c thu n tuý ch là lý thuy t. Vi c s d ng quy n p toán h c ñ ch ng minh tính ñúng ñ n c a gi i thu t ñ quy ñã ñư c m t vài tác gi th c hi n, ñi u này ch ch ng minh tính ñúng ñ n c a gi i thu t ñ quy ch không cho bi t gi i thu t y hi u qu như th nào. V n ñ là ngư i l p trình ph i t xác ñ nh xem thu t gi i nào tiêu t n ít công s c c a ngư i l p trình và tài nguyên trong máy nh t. Trư ng ð i h c Nông nghi p 1 - Giáo trình L p trình nâng cao ..............................................................- 141
Bài t p chương 5 1. Dãy s Fibonaci a1, a2, .... an ñư c ñ nh nghĩa như sau: a 1 = a2 = 1 a 3 = a2 + a1 .................... an = an-1 + an-2 L p chương trình v i vi c áp d ng tính ñ quy ñ xây d ng dãy s Fibonaci, giá tr n nh p t bàn phím. 2. L p chương trình gi i bài toán Tháp Hanoi 3. Hàm F(x,y) ñư c ñ nh nghĩa như sau: n ux=0 y +1   F ( x − 1,1) F(x,y) = n uy=0  F ( x − 1, F ( x, y − 1)) v i các trư ng h p còn l i  L p chương trình có dùng ñ quy ñ tính hàm F v i giá tr x,y nh p t bàn phím. 4. S là m t chu i ký t có ñ dài t i ña là 255. L p chương trình nh p S t bàn phím sau ñó in ra chu i ngư c c a chu i ban ñ u. Chương trình có dùng ñ quy Ví d : S = ‘Chuc mung ngay 8/3’ In ra ‘3/8 yagn gnum cuhC’ 5. Cho dãy s a1, a2, ..... , an . G i s hoán v c a dãy s là k. L p m t chương trình hi n lên s hoán v c a dãy s và giá tr c th c a t ng hoán v Ví d : dãy s 1 3 2 In ra: S hoán v = 6 Giá tr c th 1 2 3; 1 3 2; 2 1 3; 2 3 1; 3 1 2; 3 2 1 Trư ng ð i h c Nông nghi p 1 - Giáo trình L p trình nâng cao ..............................................................- 142