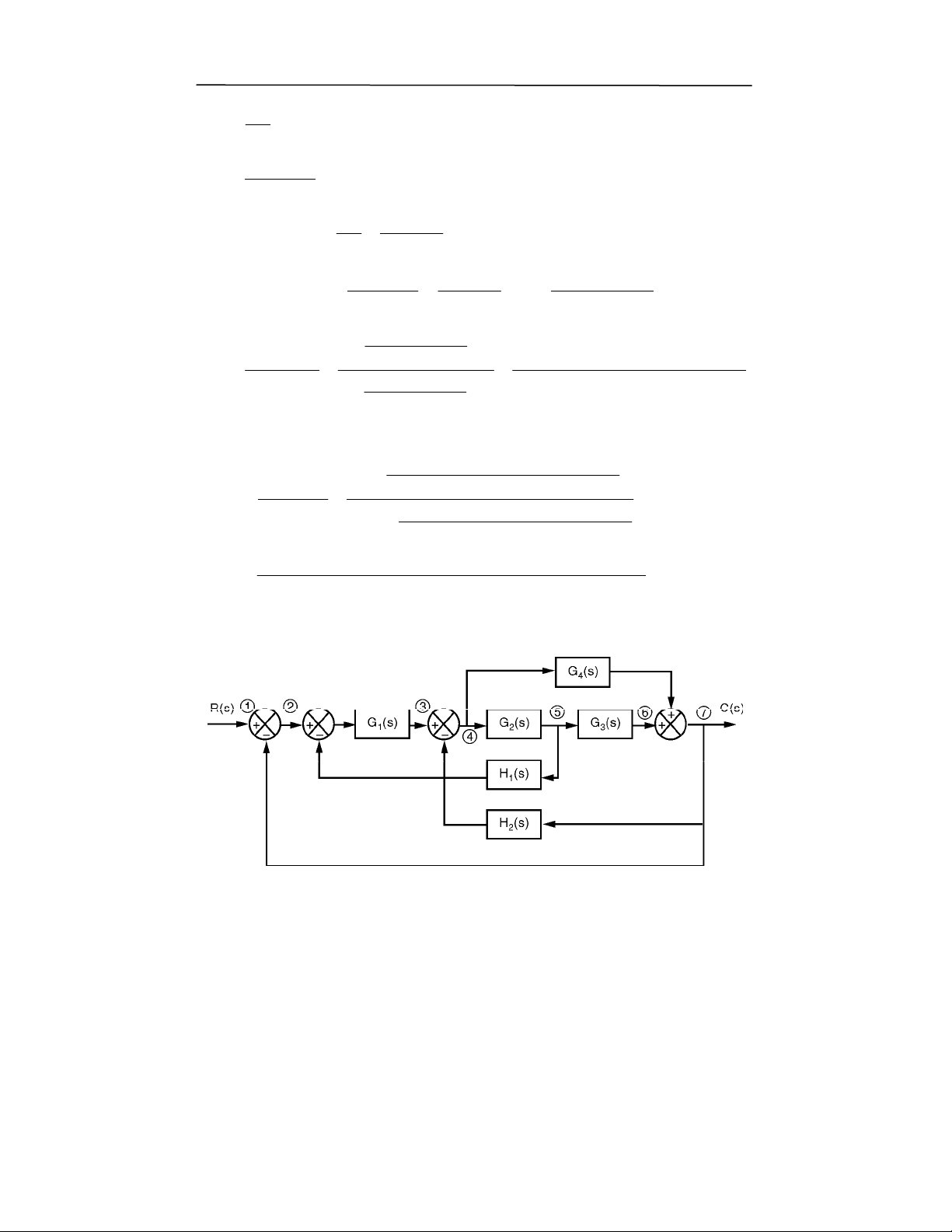
!"#$!
2
!
;
P
P
=
'
#
P
P
P ;
=+
'
' '
!
P P P P
+
= + = + =
'
' '
_ #
P P P ;
P P ;
P P P P P
P ; P P ;
. .
+
+
= = =
+ +
'
' '
' ' ' ' '
_
H
_
P P P ;
P P P ;
P P ;
PP P P ;
P ; P ; P P ; P ; ;
;
P ;
+
+
+
= = =
+
+ + + +
++
'
'
' '
'
' ' '
' '
 * A! ,:$ *# ,7F ) "7F )( $8  ,0 ;) /Ak

H
H
P P P ;
PP ; P P ; P ; ;
P P
PP P P ;
P P P
P ; P P ; P ; ;
.
.
+
+ + +
= = +
+++ + +
'
' ' '
'
' ' '
⇒
P P P P P ;
P
P ; P P ; P ; ; P P P P P ;
+
=+ + + + +
'
' ' ' '
PCGB16>6
? A! ,:$ *#, 7F) "7F) ($8  , 0;)R &$ @j 
RY)6F"0#%0;k
-BM
T;"0&,7F)"7F)6F"0#%0;76$k
 $*&  R0 ,0& )
: ,:7F( P
g'hd 6 $ "0 "0& > 5 ,:?  R0 
,0&)
>

l($*&"&!:P
:6$P
'
g'h
%
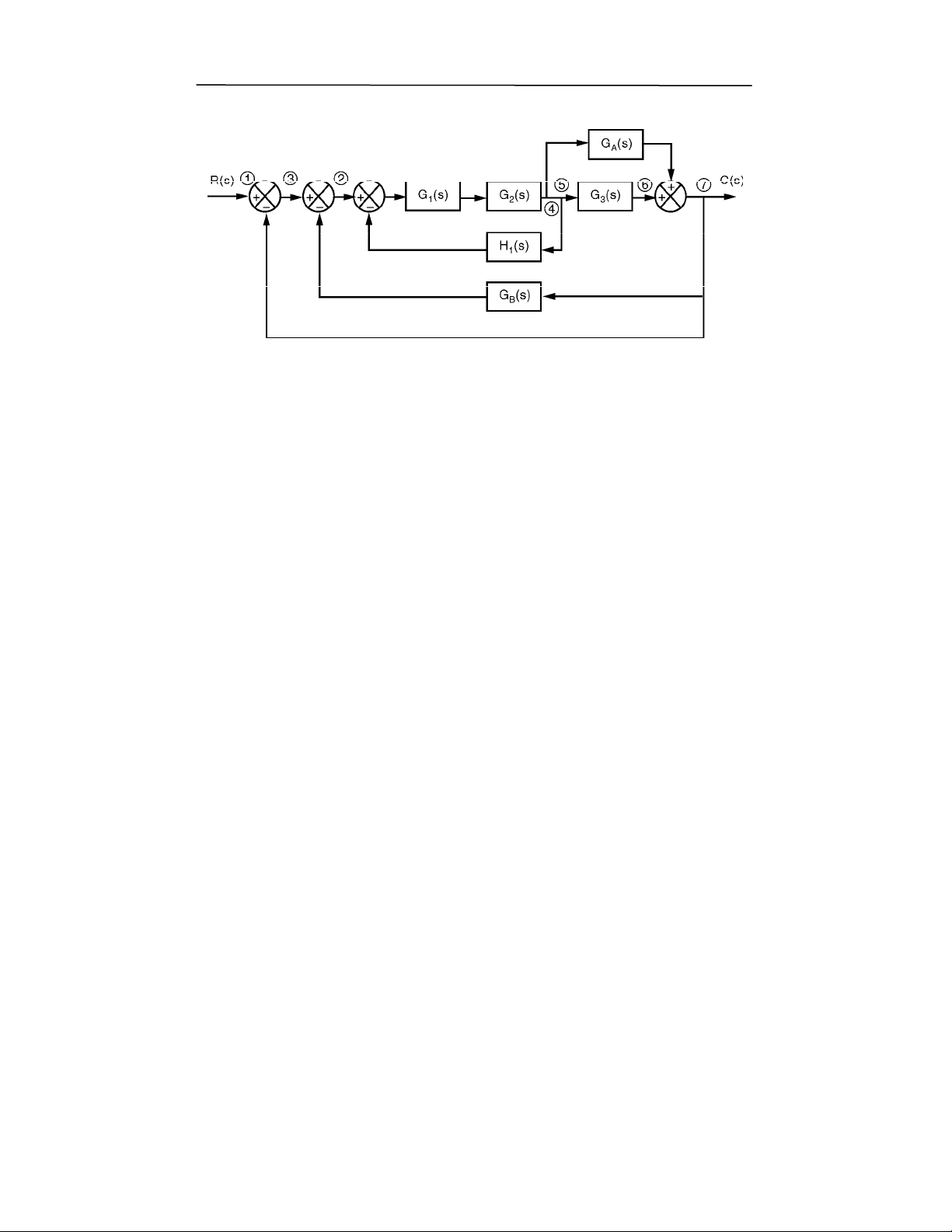
E<
H $% , 71(   9 9R ; "0& 7 , :+ ,  " 7F1 ( 6 F"0 # % 0;
,7 F) "7F )%  "F )8  0 () 8 ,;9 ,$ 1(R ; "0& " & "" ; %; ,
O$8($0;($A)
/ I
. 7F) 9 9 R ; "0&  6F "0# %0 ; / A !0 , 9 7F )
99"F)8>A,:71(O$@$A)"&,L!A!,:$*#,7F)"7F)
($ 8 , 0; ) $* ;," & !( $897 F) 9 9 R ; " 0&6F"0# % 0;
/A % 0+ )! ) ,?  ,0 ;)d !0 j6F "0# ($ 1, & (0 , & (0  #$
(( R; "0& %( $d ,$A* ,0 ,:71( )( ($8 )7FA )8 RA
,0 )0A :d % ,? A! ,:$*# ,7F) "7F) , 98 ,71(
   #$ 9 9 ,? ,: + ( ( 9+ ,7 (" 1 60 ;d" 0; >F ( (  
,0;) 97( ,19 (( 99 ,? A* * R5 #! /j U0 "0d
97F) 99 R; "0& ,7F) "7F) 6F "0# %0; (^ ,?( F19 "&
,L! A !,: $*# ,7 F)" 7F )($8 ( ( , 0;) "F )8  0; >F 
( (  , 0; )9 7( , 19 , (0 ! 0 , 9 7F) 9 9  $ O$ 8 Fd "0 / A
97 F )9 9 6 F"0 #@0A ),?  $6 P"7F 1(" #( 9"; F8 !$1( , ;9
,0
#'+
16>65Q=GC<A0I
-6&'(
 &R & $@ j ,0 ;), 71"0 ) d )0A 9 7F)9  96 78@ $1)
6F "0# %0;d , (0A (0 ,& 678 @$1) 97F) 99 6F "0# @0A) ,?
 $  P* 6 0 6    L > P @7F  " +*d L  ' 3R / A 6F " 0# @0A )
,?  $ ($8  ,0 ;) (0 6F" 0# %0;  7L ' 3 
!"#$!
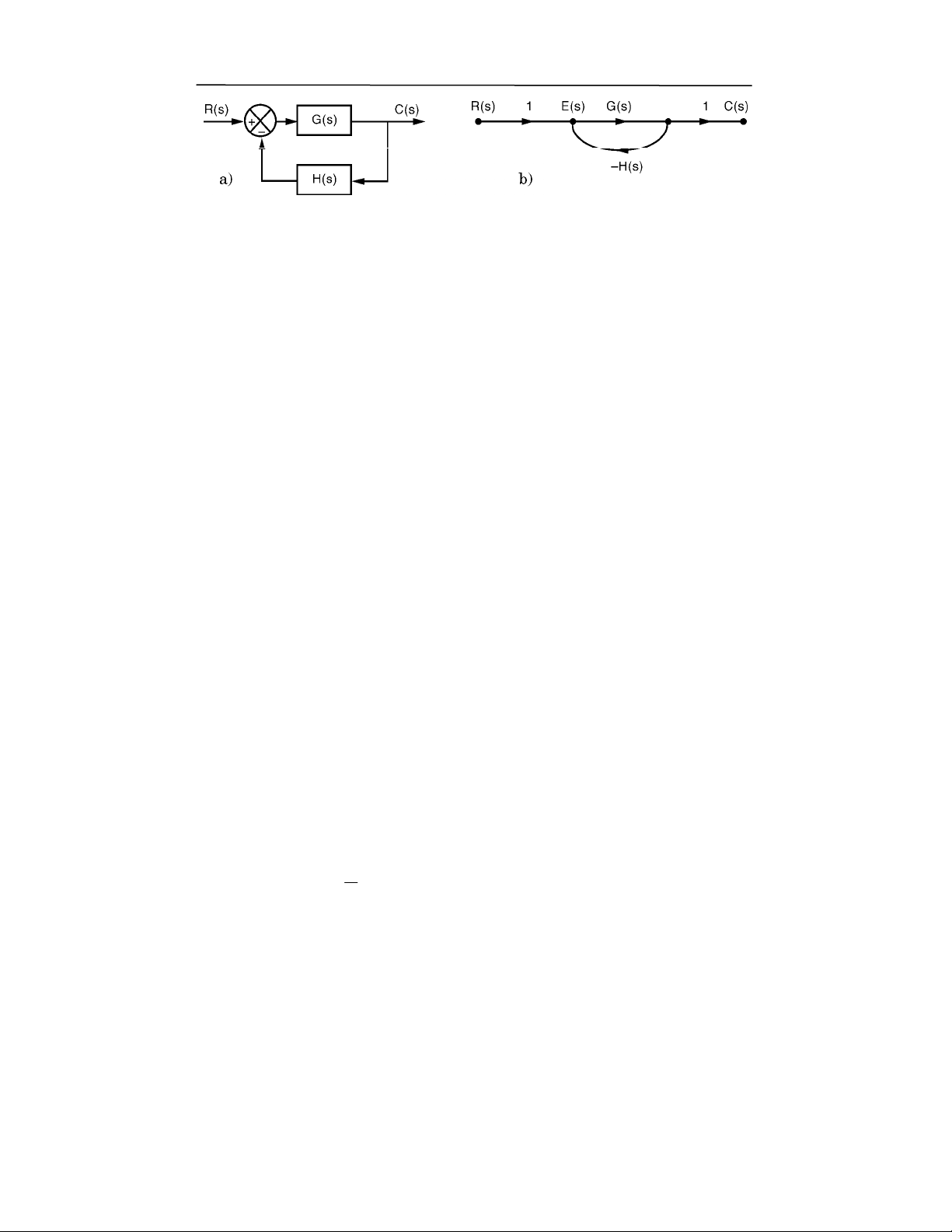
E
+,.-3#2D1X')
^V-e1^V )
&'(
HF "0# @0A ) ,?  $ /A !0 ,! 1) )0# !( (

>A
6
Z

k ! 0 , " &! R &$ @ j !0 , R ;  * ,?  $ ,:0 )  
,0;)
Z

k"7FA)0;,:71(,;9$,d,:+!0j(0!$P
, +( ^( # $,:$ *#( $8, ? $>A ( 0)  A!,: $*# (0 R ;,
!0 ; O$  )7P , ?  $ F8  $ ,
Z

k$,(^(0((7F):
Z
=C
k$,(^(0((7F)>A0
Z
B;
k$,(0(8((:>A((>A0
1  $, 0j  F1 9d , ;, ( 8 ( ( ,?   $ : " #$ R Y )  $ > A
R Y) ,0& )" 16 0; ($8 ( (,?   $ >A0 
Z
'

k"7FA))0#!((/+,;9(0($A)7F)
,?  $ ", 7A $, )$0 #" ; $ ,"? (> A( ^O $! 0j $ ,!0 ,/ #
Z
'<BD<=
k,?(($8((A!,:$*#($8((
,:+"7FA),;"0
Z
P7C
k"7FA)%9%?)0#!((/+,;9(0($A)
7 F) ,?  $> A( ^O $ !0j $ ,! 0 ,/ #
Z
'< BD<A 7C
k,?(($8((A!,:$*#($8((
,:+>0A)%?"0
.6!0 $"
 A! ,:$ *#  ,7F ) " 7F) ($8    , 0; ) ,7 1 "0 ) R& $ @ j
R Y) 6F" 0#@ 0A) ,?  $ (0 ,& ,? , 0 (0+ ), 7( k
- -
-
P
= ∆
∆∑
g'3h
%
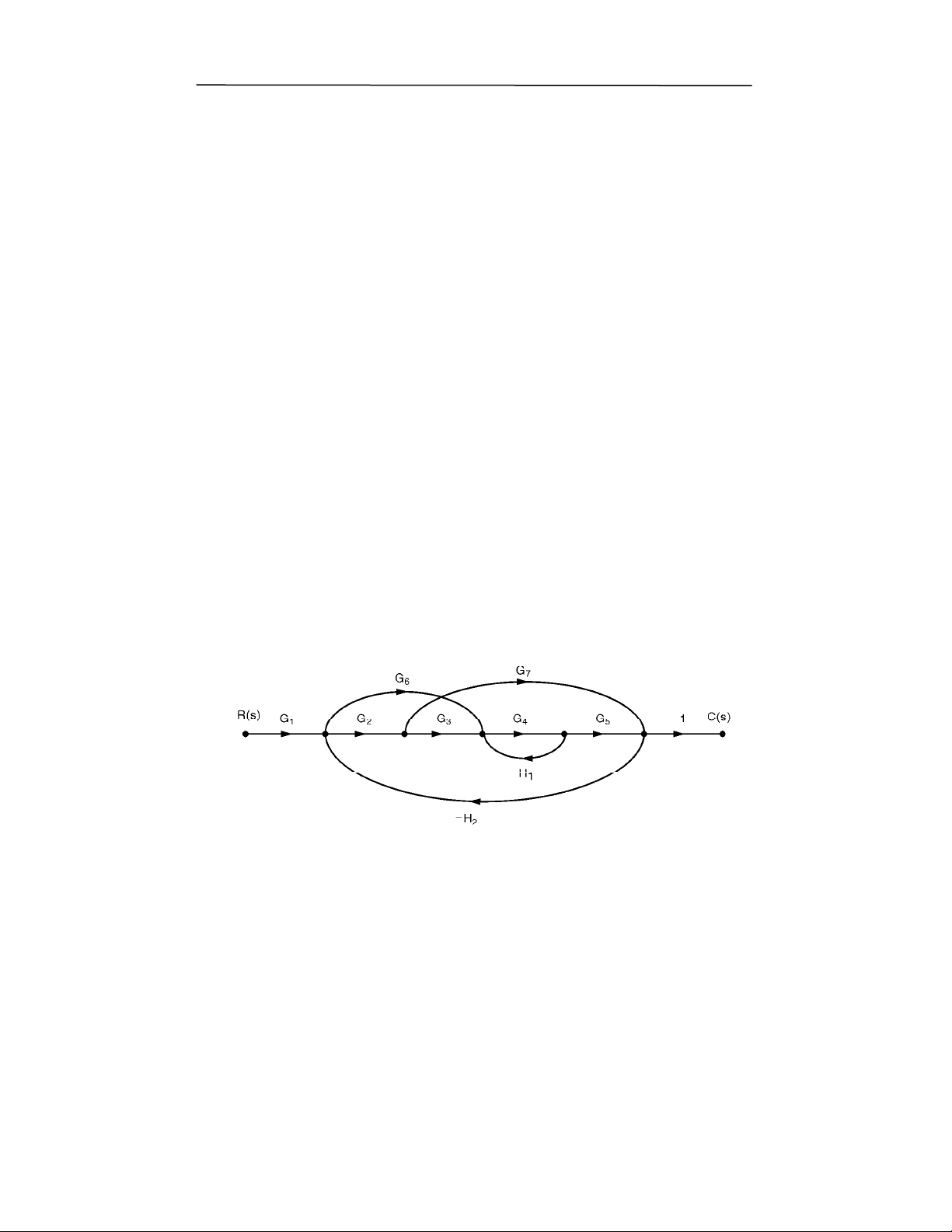
E'
,:0)"0k
•

-
Z"0 /F1($8"7FA),;,7-

•
∆Z"5,7(($86F"0#@0A),? $k
d d 6
d d 6
, , ,
∆ = − + − +
∑ ∑ ∑
g'2<h

•
∑
ii
L
Z ,0& ) "0 /F 1 >0A )( $8 ( ( >0A )% ? (0 ,:0 ) 6F "0#
      @0 A) ,?  $

•
∑
ji ji
LL
,
Z ,0& ) ( ( ,?(  "0 /F1  > 0A) ($8   > 0A)
7
GC
$

•
∑
mji mji
LLL
,,
Z , 0& ) ( ( ,?( "0 /F1  > 0A) ($ 8 R  > 0A)
7
GC
$

•
∆
-
Z"5  , 7 ( (0  ( $8 6F "0# @0 A) ,?  $∆
-
"7F1(6$*
:,7A∆RY)((R08" ((>0A)%? (0
GC
,F
"7FA),;
-0

9∗
R7GCS
p%0+)(0$,A0($)
∗
RGCS
p(0?,;,$,($)
16>610< I AC GB C D?  =G
0I
PCGB16E6
? A !,: $*# ,7F )"7 F)( $8  , 0; )! 0+, 8RF8 
6F "0# @0A ), ?  $7 6$ k
-M
Z 0 /F1 ($8 ( ( "7FA ), ; k
P P P P P
=
' 3 2
l
P P P P
=
' E 3 2
l
P P P
=
' G
Z 0 /F1 ($8 ( ( >0A )%?k
!"#$!
E
P ;
= −
3
l
P P ;
= −
' ' G '
l
P P P ;
= −
E 3 2 '
l
P P P P ;
= −
3 ' 3 2 '