THỦY TĨNH HỌC ThS LÊ MINH LƯU
_ 9 _
C
CH
HƯ
ƯƠ
ƠN
NG
G
2
2
THỦY TĨNH HỌC
§2.1 – Áp suất thủy tĩnh –Áp lực.
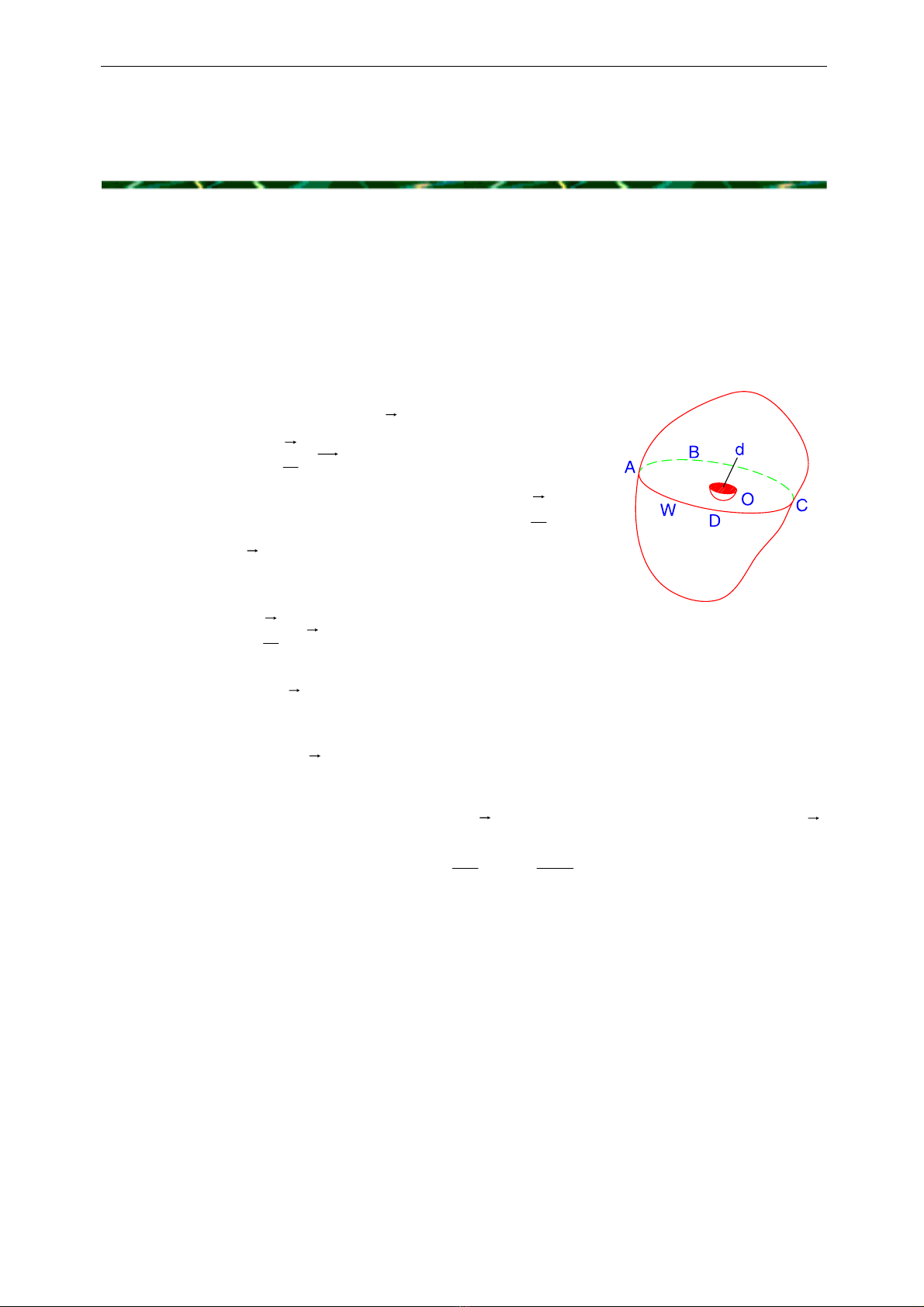
Lấy một khối chất lỏng W đứng cân bằng (hình 2 – 1). Nếu chia cắt khối đó
bằng một mặt phẳng tuỳ ý ABCD và vứt bỏ phần trên, thì muốn giữ phần dưới
khối đó ở trạng thái cân bằng như cũ ta phải thay thế tác dụng của phần trên lên
phần dưới bằng một hệ lực tương đương.
Trên mặt phẳng ABCD, xung quanh một điểm O
ω
ω
Hình 2 – 1
tuỳ ý ta lấy một diện tích ω; gọi P là lực của phần trên
tác dụng lên ω, tỉ số tb
P
P=
ω
gọi là áp suất thủy tĩnh
trung bình. Nếu diện tích ω tiến tới số 0, thì tỉ số
ω
P
tiến tới giới hạn p, gọi là áp suất thủy tĩnh tại một điểm,
hoặc nói gọn là áp suất thuỷ tĩnh.
p
P=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
→
ω
ω
lim
0
(2 – 1)
Áp suất thủy tĩnh plà ứng suất tác dụng lên một phân tố diện tích lấy trong nội
bộ môi trường chất lỏng đang xét.
Trong thuỷ lực, lực P tác dụng lên diện tích ω gọi là áp lực thủy tĩnh lên diện
tích ấy.
Chú ý: người ta thường gọi trị số p của p là áp suất thủy tĩnh và trị số P của
P
là áp lực thủy tĩnh. Áp suất có đơn vị là 2
m
N hoặc 2
.sm
kg .
Trong kỹ thuật, áp suất còn được đo bằng átmốtphe (at)
1 at = 9,81.104 (N/m2)
1 at = 1(kG/cm2)
Áp lực có đơn vị là Niutơn (N)
Áp suất còn được đo bằng chiều cao cột nước.
§2.2 – Hai tính chất cơ bản của áp suất thủy tĩnh.
Tính chất 1: Áp suất thủy tĩnh tác dụng thẳng góc với diện tích chịu lực và hướng
vào diện tích ấy.
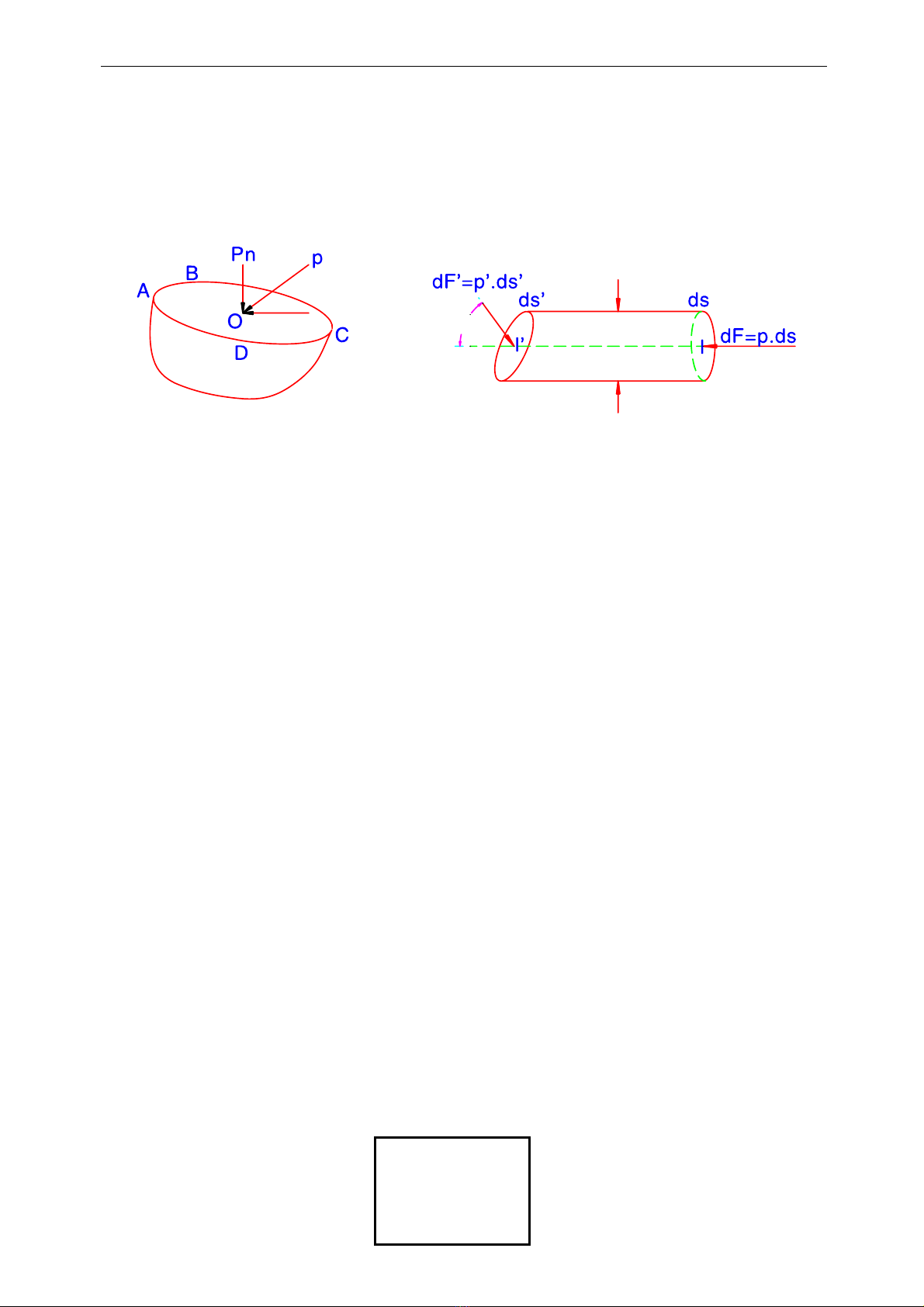
Áp suất thủy tĩnh tại điểm O lấy trên mặt phân chia ABCD (hình 2 – 2) là một
lực có thể chia làm hai thành phần: pn theo hướng pháp tuyến tại điểm O của mặt
THỦY TĨNH HỌC ThS LÊ MINH LƯU
_ 10 _
ABCD và τ theo hướng tiếp tuyến. Thành phần τ có tác dụng làm mặt ABCD di
chuyển, tức chất lỏng có thể chuyển động tương đối, nhưng như đã giả thiết ban
đầu, chất lỏng đang xét ở trạng thái tĩnh nên phải có τ = 0 và chỉ còn lại thành
phần pháp tuyến pn. Thành phần pn không thể hướng ra ngoài được vì chất lỏng
không chống lại được sức kéo mà chỉ chịu được sức nén. Vậy áp suất p tại điểm O
chỉ có thành phần pháp tuyến và hướng vào trong.
t
α
Hình 2 – 2 Hình 2 – 3
Tính chất 2: Trị số áp suất thủy tĩnh tại một điểm bất kỳ không phụ thuộc hướng
đặt của diện tích chịu lực tại điểm này.
Lấy một phân tố diện tích ds có tâm I và một hình trụ vô cùng nhỏ có tiết diện
thẳng ds (hình 2 – 3). Đáy kia hình trụ có diện tích dS' và tâm I', đáy này có hướng
bất kỳ xác định bởi góc α. Những kích thước về chiều dài là những vô cùng nhỏ.
Gọi p và p' là những áp suất, chúng vuông góc với những mặt tương ứng.
Theo định nghĩa, ta có các trị số áp lực dF và dF' như sau:
dF = p.dS
dF' = p'.dS'
Hình trụ này đứng cân bằng dưới tác dụng của những lực mặt là vô cùng nhỏ
bậc hai và của những thể tích là những vô cùng nhỏ bậc ba. Do đó ta có thể bỏ
qua những lực thể tích. Phương trình này chiếu lên trục II', cho ta:
0cos' =−
α
dFdF (2 – 2)
Vì những lực mặt tác dụng lên mặt bên và vuông góc với II', đã triệt tiêu nhau.
Vậy: pdS = p'.dS'cosα; vì dS = dS'cosα nên ta rút ra:
'pp = (2 – 3)
Vậy áp suấtt thủy tĩnh tại điểm I là một đại lượng vô hướng p, chỉ phụ thuộc vị
trí của điểm I, nghĩa là trong hệ tọa độ vuông góc Oxyz thì:
p = f(x, y, z) (2 – 4)
Từ hai tính chất trên của áp suất thủy tĩnh, ta thấy rõ các thành phần tiếp tuyến
đều bằng số không và các thành phần pháp tuyến đều bằng nhau và bằng p. Vì vậy
tensơ ứng suất viết cho áp suất thủy tĩnh có dạng
p 0 0
0 p 0
0 0 p
THỦY TĨNH HỌC ThS LÊ MINH LƯU
_ 11 _
§2.3 – Phương trình vi phân cơ bản của chất lỏng cân bằng
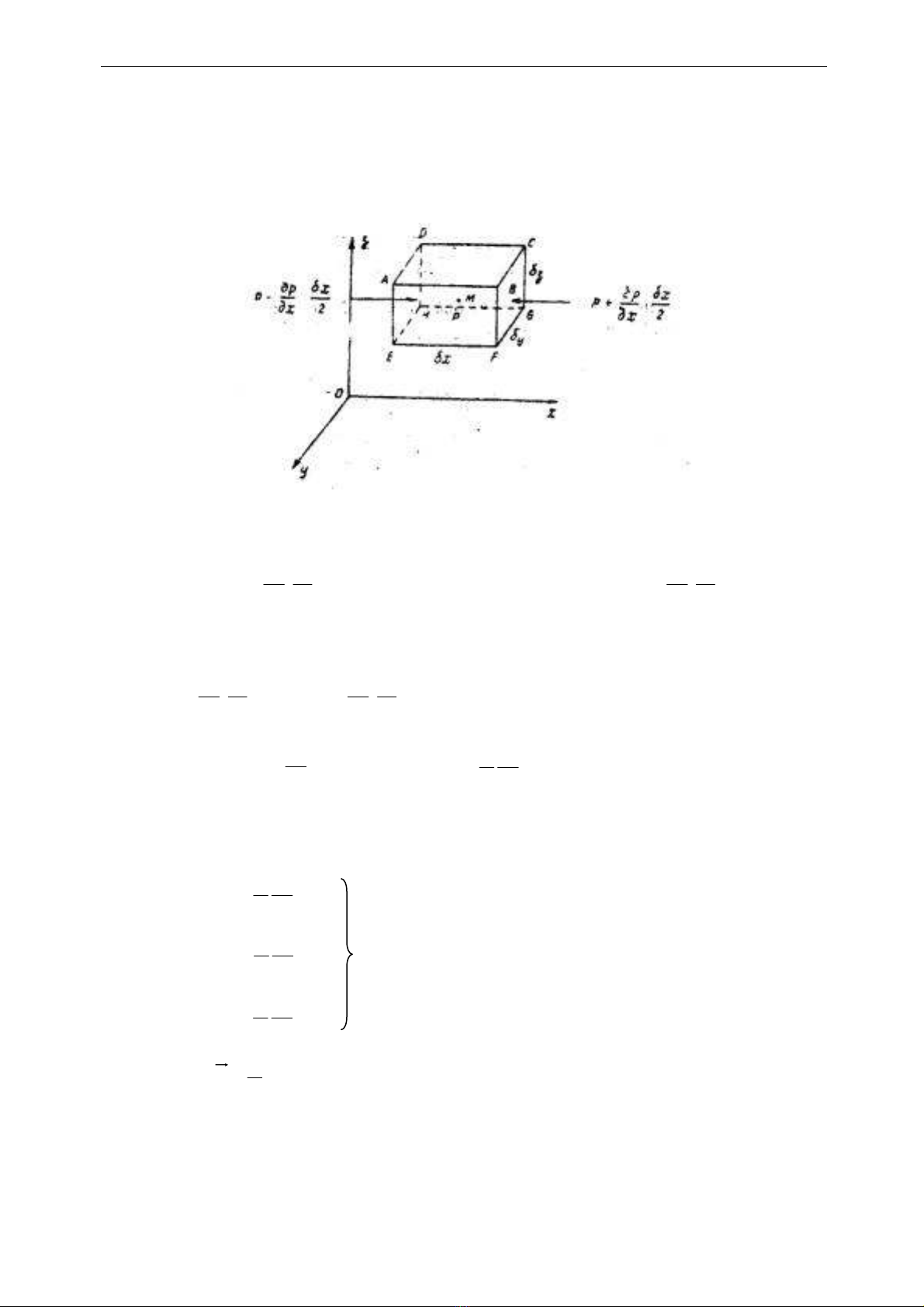
Xét khối chất lỏng hình hộp vô cùng nhỏ ABCDEFGH có cạnh δx, δy, δz (hình
2 – 4) đứng cân bằng. Điều kiện cân bằng là tổng số hình chiếu trên các trục của
các lực mặt và lực thể tích tác dụng lên khối đó bằng không.
Hình 2 – 4.
Gọi p là áp suất tại trọng tâm M của hình hộp, thì áp suất at5i trọng tâm mặt
ADHE bằng ⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−2
.x
x
p
p
δ
, tại trọng tâm mặt BCGF bằng ⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+2
.x
x
p
p
δ
; gọi Fx là
thành phần trên trục Ox của lực thể tích F tác dụng lên lên một đơn vị khối lượng
chất lỏng, ta có thể viết điều kiện cân bằng của hình hộp theo phương x như sau:
0.
2
.
2
.=+
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
+−
⎟
⎠
⎞
⎜
⎝
⎛
∂
∂
−zyxFzy
x
x
p
pzy
x
x
p
px
δδδρδδ
δ
δδ
δ
rút gọn ta có: 0=+
∂
∂
−x
F
x
p
ρ
hoặc 0
1=
∂
∂
−x
p
Fx
ρ
Suy luận tương tự đối với những hình chiếu các lực trên các trục Oy, Oz và viết
toàn bộ hệ thống phương trình biểu thị sự cân bằng của khối hình hộp, ta có:
0
1=
∂
∂
−x
p
Fx
ρ
0
1=
∂
∂
−y
p
Fy
ρ
(2 – 5)
0
1=
∂
∂
−z
p
Fz
ρ
hoặc 0
1=− gradpF
ρ
Đó là hệ phương trình vi phân cơ bản của chất lỏng đứng cân bằng và còn gọi
là hệ phương trình Ơle (do Ơle tìm ra năm 1755). Phương trình này biểu thị quy
luật chung về sự phụ thuộc áp suất thủy tĩnh đối với toạ độ:
p = f(x, y, z)
THỦY TĨNH HỌC ThS LÊ MINH LƯU
_ 12 _
Hệ (2 – 5) có thể viết dưới dạng vi phân toàn phần của p như sau: nhân những
phương trình trong hệ (2 – 6) riêng biệt với dx, dy, dz rồi công vế đối vế, ta có:
()
0
1=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
+
∂
∂
+
∂
∂
−++ dz
z
p
dy
y
p
dx
x
p
dzFdyFdxF zyx
ρ
(2 – 6)
Vì p = f(x, y, z) chỉ là hàm số của toạ độ, nên ta co thể viết được:
()
0
1=−++ dpdzFdyFdxF zyx
ρ
hoặc dp = ρ(Fxdx + Fydy + Fzdz) (2 – 7)
Phương trình (2 – 7) gọi là phương trình vi phân cân bằng của chất lỏng.
§2.4 – Mặt đẳng áp.
Mặt đẳng áp là mặt có áp suất thủy tĩnh tại mọi điểm đều bằng nhau, tức là mặt
có p = const, do đó dp = 0.
Phương trình vi phân của mặt đẳng áp:
Fxdx + Fydy + Fzdz = 0 (2 – 8)
Tính chất 1: Hai mặt đẳng áp khác nhau không thể cắt nhau.
Tính chất 2: Lực thể tích tác dụng lên mặt đẳng áp thẳng góc với mặt đẳng áp.
§2.5 – Sự cân bằng của chất lỏng trọng lực
Khi lực thể tích tác dụng vào chất lỏng chỉ là trọng lực thì chất lỏng được gọi là
chất lỏng trọng lực.
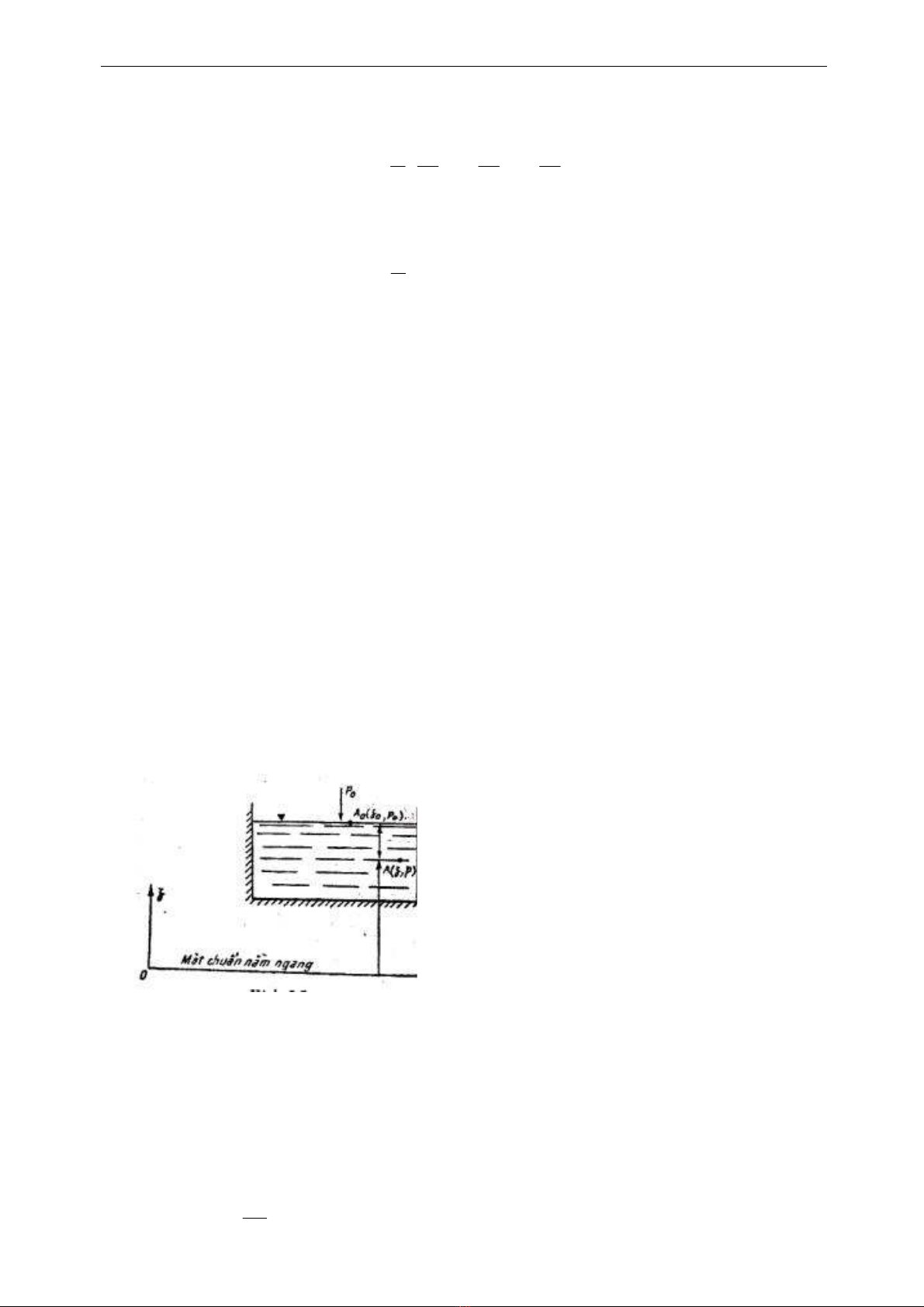
Trong hệ tọa độ vuông góc mà
trục Oz đặt theo phương thẳng đứng
hướng lên trên, thì đối với lực thể tích
F tác dụng lên một một đơn vị khối
lượng của chất lỏng trọng lực, ta có
Fx = 0, Fy = 0 và Fz = -g (g là gia tốc
rơi tự do) (hình 2 – 5)
Hình 2 – 5.
1. Phương trình cơ bản của chất lỏng ở trạng thái cân bằng.
Từ (1 – 7), thay Fx = 0, Fy = 0, Fz = -g ta có:
dp = -ρgdz (2 – 9)
Sau khi tích phân và chia cho ρg ta có:
const
g
p
z=+
ρ
(với γ = ρg) (2 – 10)
THỦY TĨNH HỌC ThS LÊ MINH LƯU
_ 13 _
Từ (2 – 10) xét tại hai điểm A và A0 ta được:
const
p
z
p
z=+=+
γγ
0
0 (2 – 11)
hoặc p = p0 + γ(z0 – z) (2 – 11)'
Gọi z0 là tung độ của điểm ở trên mặt tự do và h là độ sâu của điểm đang xét có
tung độ z, ta có: h = z0 – z.
Nên (2 – 11)' co thể viết:
(2 – 12)
p hp=0
γ
Phương trình (2 – 11); (2 – 12) là phương trình cơ bản của thủy tĩnh học, biểu
thị quy luật phân bố áp suất thủy tĩnh trong chất lỏng đứng cân bằng. Số hạng
γ
p
có thứ nguyên là độ dài.
2. Mặt đẳng áp của chất lỏng trọng lực.
Trong trường hợp đang xét lực khối là lực trọng trường, gia tốc là gia tốc rơi tự
do g, vì vậy trong hệ tọa độ đã chọn hình chiều của lực khối đơn vị trên trục Ox,
Oy, Oz sẽ là: Fx = 0, Fy = 0, Fz = -g, còn phương trình mặt đẳng áp được viết dưới
dạng:
- g.dz = 0; do g ≠ 0 nên z = const.
Do vậy mặt đẳng áp trong chất lỏng tĩnh đồng nhất sẽ là các mặt nằm ngang bất
kỳ, trong đó có cả mặt thoáng, không phụ thuộc vào hình dạng bìng chứa chất
lỏng. Mặt nằm ngang cũng sẽ là mặt phân cách của hai loại chất lỏng cùng chứa
trong một bình.
Ví dụ 1: Tìm áp suất tại một điểm ở đáy bể đựng nước sâu 4m, trọng lượng đơn
vị của nước γ = 9810 N/m3 (γ = 1000kG/m3). Áp suất tại mặt thoáng p0 =
98100N/m2 (p0 = 10.000kG/m2).
Giải:
Áp dụng công thức (2 – 12) ta có:
p = p0 + γh = 98100 + 9810x4 = 137.340 N/m2 ( = 14.000kG/m2)
3. Định luật bình thông nhau.
Hai bình thông nhau chứa đựng chất lỏng khác nhau và có áp suất trên mặt
thoáng bằng nhau, độ cao của chất lỏng ở mỗi bình tính từ mặt phân chia hai chất
lỏng đến mặt thoáng sẽ tỷ lệ nghịch với trọng lượng đơn vị của chất lỏng, tức là:
1
2
2
1
γ
γ
=
h
h (2 – 13)
Trong đó h1, h2 là những độ cao nói trên ứng với những chất lỏng có trọng
lượng đơn vị γ1, γ2. Thực vậy, áp suất p1, p2 trên cùng mặt phân chia A – B (hình 2
– 6) bằng nhau.