TỔN THẤT CỘT NƯỚC TRONG DÒNG CHẢY ThS LÊ MINH LƯU
_ 52 _
C
CH
HƯ
ƯƠ
ƠN
NG
G
4
4
TỔN THẤT CỘT NƯỚC TRONG DÒNG CHẢY
§4.1 – Những dạng tổn thất cột nước.
Trong phương trình Becnuly viết cho toàn dòng chảy thực, số hạng hw là năng
lượng của một đơn vị trọng lượng chất lỏng bị tổn thất để khắc phục sức cản của
dòng chảy trong đoạn dòng đang xét. Ta còn gọi hw là tổn thất cột nước
Ta chia tổn thất cột nước làm làm hai dạng:
− Tổn thất dọc đường sinh ra trên toàn bộ chiều dài dòng chảy đều hoặc
không đều đổi dần. Là tổn thất xảy ra dọc theo đường di chuyển của dòng chảy do
sự ma sát của chất lỏng với thành rắn tiếp xúc. Ta ký hiệu tổn thất này là hd.
− Tổn thất cục bộ sinh ra tại những nơi cá biệt, ở đó dòng chảy bị biến dạng
đột ngột; ký hiệu tổn thất này là hc. Thí dụ: tổn thất tại nơi ống uốn cong, ống mở
rộng, nơi có đặt khóa nước v…v...
Nguyên nhân của tổn thất cột nước: dù dưới dạng nào cũng do ma sát giữa các
phần tử chất lỏng tức do ma sát trong sinh ra. Công tạo nên bởi lực ma sát này biến
thành nhiệt năng mất đi không thể lấy lại cho dòng chảy.
Với giả thiết là các dạng tổn thất trên xảy ra độc lập đối với nhau, thì tổn thất
năng lượng hw của dòng chảy có thể viết:
hw = Σhd + Σhc (4 – 1)
Trong đó: Σhd tổng cộng các tổn thất dọc đường của dòng chảy; Σhc tổng các tổn
thất cục bộ của dòng chảy.
§4.2 – Phương trình cơ bản của dòng chất lỏng chảy đều.
Ta cần tìm mối quan hệ giữa tổn thất cột nước dọc đường với sức cản ma sát
trong dòng chảy đều.
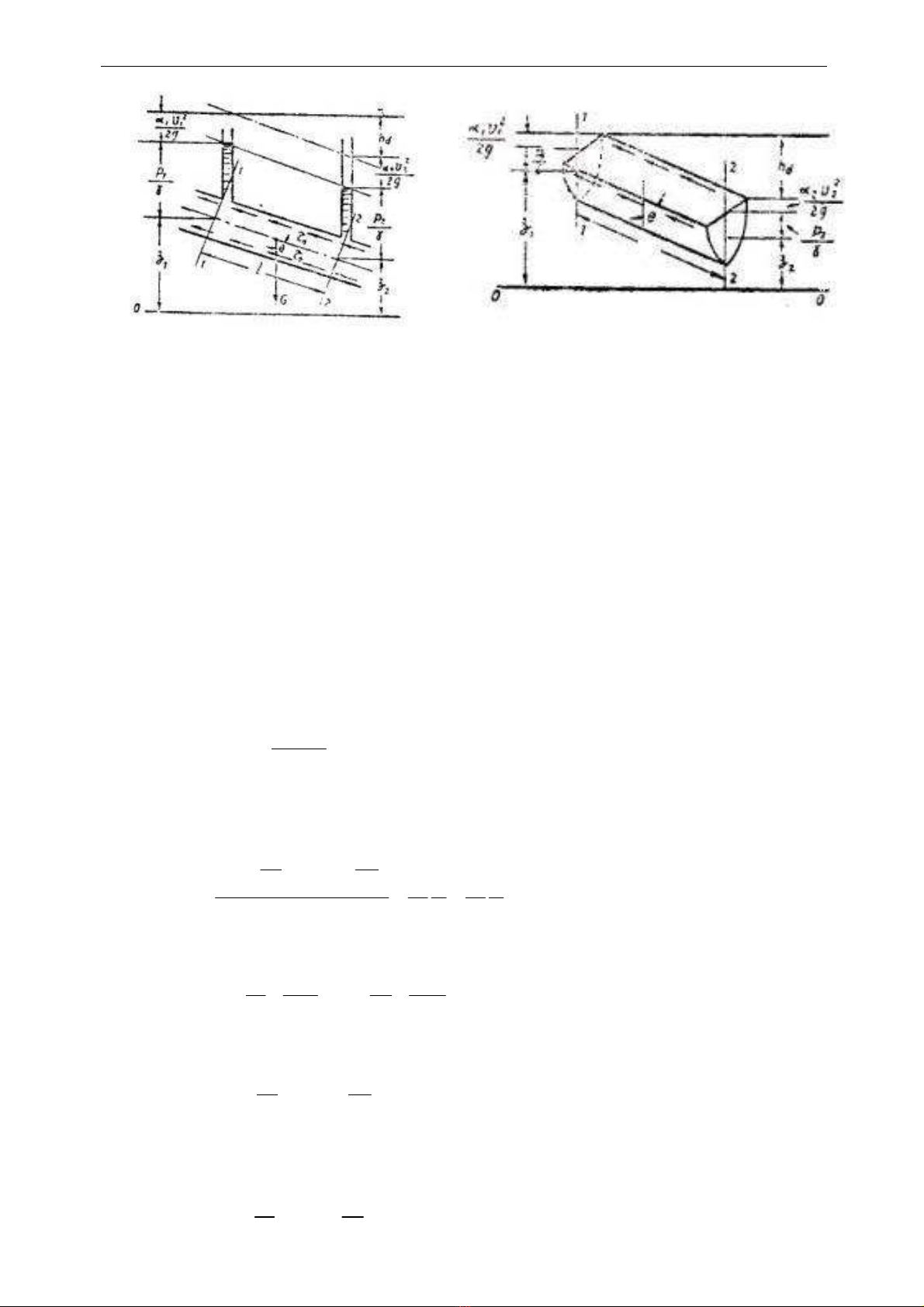
Trong dòng chảy đều có áp hoặc không áp, ta lấy một đoạn dòng dài l giới hạn
bởi những mặt cắt ướt 1 – 1 và 2 – 2 (hình 1 – 4a và 1 - 4b), phương chảy lập với
phương thẳng đứng một góc bằng θ.
Gọi ω là diện tích mặt cắt ướt, trong dòng chảy đều ω = const dọc theo dòng
chảy.
Độ cao trọng tâm của mặt cắt 1 – 1 và 2 – 2 đối với mặt chuẩn nằm ngang 0
– 0 là z1 và z2; Áp suất thủy động tại những trọng tâm áp là p1 và p2
Các ngoại lực tác dụng lên đoạn dòng chất lỏng chảy đều, chiếu theo phương
của trục dòng chảy là:
− Lực khối lượng: Ở đây lực khối lượng duy nhất là trọng lực G = γωl, có
điểm đặt tại trọng tâm dòng chảy; hình chiếu của nó lên trục dòng chảy là cosθ =
γωlcosθ. Trong dòngc hảy đều không có gia tốc nên lực quán tính bằng không.
TỔN THẤT CỘT NƯỚC TRONG DÒNG CHẢY ThS LÊ MINH LƯU
_ 53 _
Hình 4 – 1.
a) b)
− Lực mặt:
+ Có động áp lực P1 = p1ω và P2 = p2ω tác dụng thẳng góc với mặt cắt ướt;
song song với phương của trục dòng và hướng vào nội bộ của đoạn dòng, còn áp
lực thủy động tác dụng lên mặt bên của đoạn dòng đều thẳng góc với trục dòng, do
đó hình chiếu lên trục dòng bằng không.
+ Ở mặt bên của đoạn dòng đang xét còn sức ma sát đặt ngược chiều chảy,
bằng tích số của ứng suất tiếp tuyến τ0 với diện tích mặt bên: τ0χl, trong đó χ là
chu vi ướt.
Vì là dòng chảy đều, tức chuyển động không có gia tốc, nên tổng số hình chiếu
các lực trên phương trục dòng bằng không:
p1ω – p2ω – τ0χL + γωlcosθ = 0 (4 – 2)
Từ hình vẽ ta thấy:
l
zz 21
cos −
=
θ
(4 – 3)
Thay trị số cosθ ở (4 – 3), và chia số ạhng (4 – 2) cho trọng lượng G = γωl ta
được:
Rl
p
z
p
z1
00
2
2
1
1
γ
τ
ω
χ
γ
τ
γγ
==
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+
(4 – 4)
Mặt khác, viết phương trình Becnuly cho mặt cắt 1 – 1 và 2 – 2
d
h
g
vp
z
g
vp
z+++=++ 22
2
222
2
2
111
1
α
γ
α
γ
Trong trường hợp dòng chảy đều là có áp ta có: v1 = v2 và α1 = α2; do đó:
d
h
p
z
p
z=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+
γγ
2
2
1
1 (4 – 5)
Trong trường hợp dòng chảy đều là không áp ta có: v1 = v2 ; α1 = α2 và p1= p2,
do đó:
d
hzz
p
z
p
z=−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛+21
2
2
1
1
γγ
(4 – 6)
TỔN THẤT CỘT NƯỚC TRONG DÒNG CHẢY ThS LÊ MINH LƯU
_ 54 _
Thay (4 – 6) và (4 – 5) vào (4 – 4) , ta được: l
h
R
d
=
γ
τ
0
Trong dòng chảy đều, tổn thất cột nước chỉ là tổn thất dọc đường, và tỷ số
l
hd
là độ dốc thủy lực J nên:
RJ=
γ
τ
0 (4 – 7)
Đó là phương trình cơ bản của dòng chảy đều, đúng cho cả dòng chảy có áp và
không áp. Phương trình này đặt mối liên hệ giữa tổn thất cột nước dọc đường với
ma sát là ứng suất tiếp. Sự tổn thất cột nước đó phụ thuộc vào trạng thái chảy của
chất lỏng. Do tổn thất cột nước của dòng không ổn định hoặc ổn định không đều
rất khó tính, nên thường phải giả thiết là có thể mượn công thức tổn thất cột nước
dòng đều để tính.
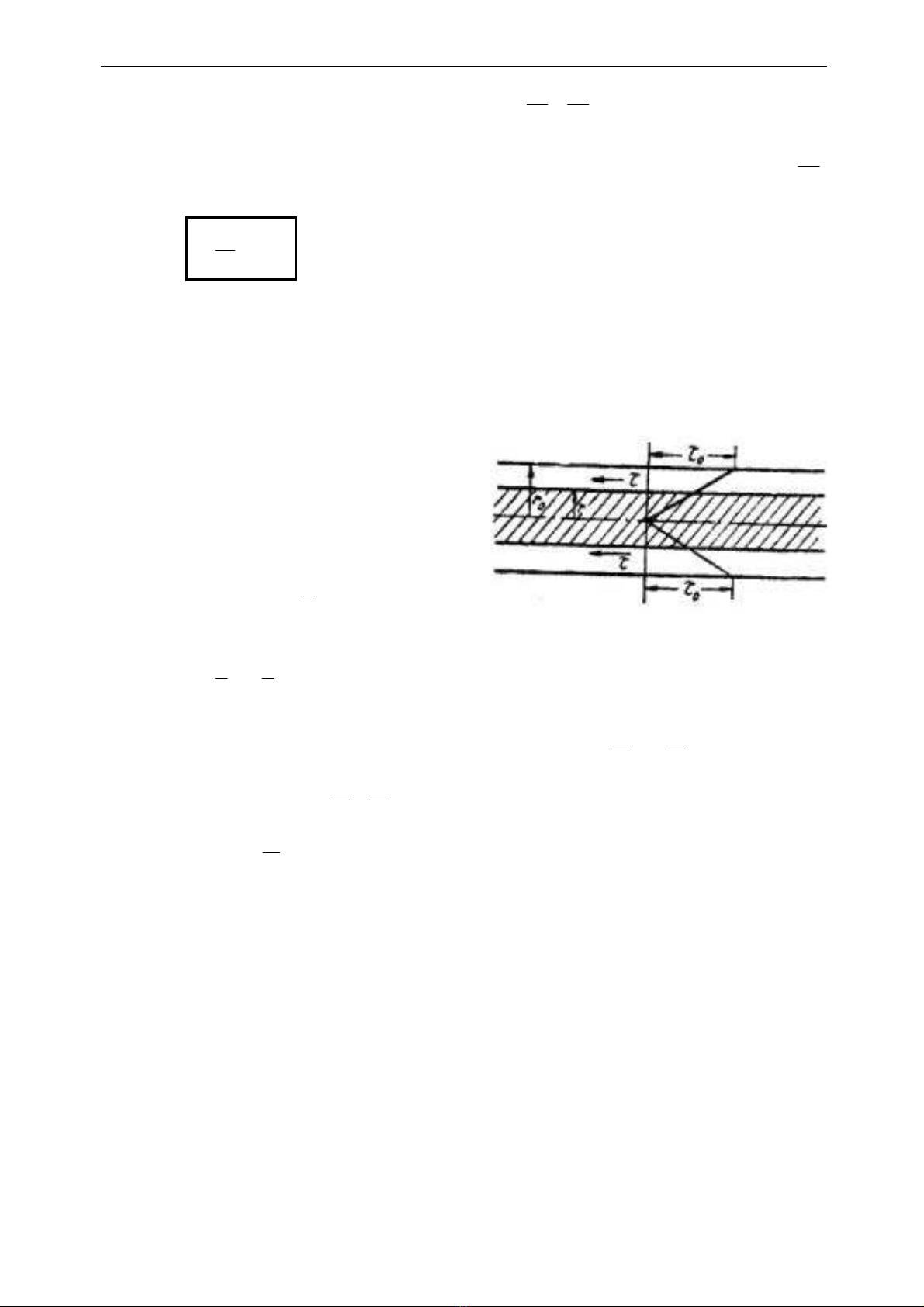
Hình 4 – 2
Nhận xét: Theo cách lập luận trên,
đối với dòng chảy đều có áp, phương
trình còn đúng cho phần của dòng chảy
đều có bán kính r < r0. Ở phần này, ta
có gọi τ là ứng suất tiếp, bán kính thủy
lực được tính bằng 2
r
R=; theo (4 – 7)
ta viết:
2
r
J=
γ
τ
(4 – 8)
Đối với toàn ống bán kính r0, ứng suất tiếp τ0, ta viết: 2
OO r
J=
γ
τ
. Chia hai đẳng
thức trên vế đối vế, ta có:
00 r
r
=
τ
τ
; hoặc:
hoặc
0
0r
r
ττ
= (4 – 9)
Vậy: ứng suất tiếp biến thiên theo quy luật bậc nhất trên mặt cắt ống: Tại tâm
ống (r = 0) ứng suất tiếp bằng không; tại thành ống r = r0 ứng suất đạt giá trị cực
đại τ0 (hình 4 – 2)
Quy luật bậc nhất này cũng đúng cho dòng chảy không áp.
§4.3 – Hai trạng thái chuyển động của chất lỏng.
1. Thí nghiệm Rây-nôn (Reynolds).
Trong thực tế tồn tại hai trạng thái chảy khác nhau của chất lỏng nhớt. Tùy theo
trạng thái chảy mà cấu tạo của dòng chảy, sự phân bố lưu tốc, sự phân bố ứng suất
tiếp, tổn thất năng lượng v…v... có những quy luật khác nhau.
Thí nghiệm Râynôn trình bày một cách sơ lược như sau (hình 4 – 3): Một thùng
A khá lớn chứa nước, gắn vào nó một ống thủy tinh dài T, có đường kính không
TỔN THẤT CỘT NƯỚC TRONG DÒNG CHẢY ThS LÊ MINH LƯU
_ 55 _
đổi: một đầu ống này cắm sâu vào trong
Hình 4 – 3
thùng A có miệng vào hình loa L để cho
nước đi vào ống được thuận. Ở đầu kia
ống có khoá B để điều chỉnh lưu lượng đi
qua ống, phía dưới chổ ra của ống T đặt
một thang đo lưu lượng. Phía trên thùng A
đặt bình D đựng nước màu có tỷ trọng của
nước; gắn vào bình D một ống nhỏ, ở đầu
kia ống nhỏ này lắp một cái kim để dẫn nước
màu từ bình vào ống, trên ống nhỏ có khoá K
để điều chỉnh lưu lượng nước màu:
Trình tự thí nghiệm như sau:
Trước hết giữ nước trong thùng A cố
định, không dao động. Bắt đầu thí nghiệm,
mở khóa B rất ít cho nước chảy từ thùng A
vào ống T. Đợi sau vài phút để dòng chảy trong ống ổn định, mở khóa K cho nước
màu chảy vào ống. Lúc này quan sát ống thủy tinh T, ta thấy hiện lên một vệt màu
nhỏ căng như sợi chỉ, điều này chứng tỏ rằng dòng màu và dòng nước trong ống
chảy riêng rẻ không xáo lộn lẫn nhau. Nếu mở khóa từ từ thì hiện tượng trên có thể
tiếp tục trong một thời gian nào đó. Khi mở đến một mức nhất định (lưu tốc trong
ống đạt tới một trị số nào đó) thì vệt màu bị dao động thành sóng. Tiếp tục mở
khóa nữa, vệt màu bị đứt đoạn, sau cùng hoàn toàn hòa lẫn trong dòng nước; lúc
này dòng màu xáo trộn vào dòng nước trong ống (hình 4 – 3a, b, c).
Trạng thái chảy trong đó các phần tử chất lỏng chuyển động theo những
tầng lớp không xáo lộn vào nhau gọi là trạng thái chảy tầng.
Trạng thái chảy trong đó các phần tử chất lỏng chuyển động vô trật tự, xáo
trộn vào nhau gọi là trạng thái chảy rối.
Thí nghiệm mô tả ở trên là thí nghiệm về sự chuyển biến từ trạng thái chảy tầng
sang trạng thái chảy rối.
Nếu ta làm ngược lại, tức là vặn khóa nhỏ lại cho lưu tốc trong ống từ lớn đến
nhỏ thì thấy đến một lúc nào đó vệt màu đang không rõ lại dần dần xuất hiện và
cuối cùng hiện rõ thành sợi chỉ màu, tức là dòng chảy đang từ trạng thái chảy rối
chuyển sang chảy tầng.
Trạng thái chảy quá độ từ rối sang tầng hoặc từ tầng sang rối gọi là trạng thái
chảy phân giới.
Lưu tốc ứng với dòng chảy chuyển từ trạng thái tầng sang trạng thái rối gọi là
lưu tốc phân giới trên. Ký hiệu là vKtrên. Lưu tốc ứng với dòng chảy chuyển từ
trạng thái rối sang trạng thái tầng gọi là lưu tốc phân giới dưới. Ký hiệu là vKdưới.
Qua thí nghiệm thấy: vKtrên > vKdưới. Lưu tốc phân giới không những phụ thuộc
vào loại chất lỏng mà còn phụ thuộc vào đường kính ống làm thí nghiệm.
2. Tiêu chuẩn phân biệt hai trạng thái chảy
Dựa vào kết quả nhiều thí nghiệm, Râynôn đã dùng một đại lượng không thứ
nguyên để đặc trưng cho trạng thái chảy, đó là số Râynôn, ký hiệu Re.
TỔN THẤT CỘT NƯỚC TRONG DÒNG CHẢY ThS LÊ MINH LƯU
_ 56 _
ν
vd
Re= (4 – 10)
Trong đó:
v – lưu tốc trung bình mặt cắt
ν – hệ số động học nhớt.
d – đường kính ống
Số Râynôn có thể coi là tỷ số giữa lực quán tính và lực ma sát nhớt. Thực vậy, vì
lực quán tính là W
dt
du
F
ρ
=
1và lực nhớt là S
dn
du
F
μ
=
2 (trong đó: W là thể tích và S
là diện tích).
Nên tỉ số giữa chúng:
νν
μ
ρ
vl
S
W
dt
dn
S
dn
du
W
dt
du
F
F===
2
1 (4 – 11)
Trị số Râynôn tương ứng với trạng thái phân giới từ chảy tầng sang chảy rối,
hoặc ngược lại từ chảy rối sang chảy tầng, gọi là trị số Râynôn phân giới ReK
Ứng với vKtrên, ta có số Râynôn phân giới trên:
ν
dv
RKtren
Ktren
e= (4 – 12)
Ứng với vKdưới, ta có số Râynôn phân giới dưới:
ν
dv
RKduoi
Kduoi
e= (4 – 13)
Trạng thái chảy ứng với số Râynôn Re < ReKdưới bao giờ cũng là chảy tầng.
Trạng thái chảy có Re > ReKtrên bao giờ cũng là chảy rối.
Trạng thái chảy có ReKdưới < Re < ReKtrên có thể là chảy tầng hoặc là chảy rối,
nhưng thường là chảy rối.
Qua nhiều thí nghiệm người ta thấy rằng ReKtrên không có một trị số xác định,
thường dao động từ 12.000 đến 50.000. Trái lại ReKdưới đối với mọi loại chất lỏng
và đối với các đường kính khác nhau đều có một trị số không đổi và bằng 2320.
Do đó ReKdưới được dùng làm tiêu chuẩn để phân biệt trạng thái chảy. Ta có thể
coi rằng:
Khi Re < 2320 sẽ có trạng thái chảy tầng.
Khi Re > 2320 sẽ có trạng thái chảy rối.
Đối với kênh dẫn, ta dùng bán kính thủy lực R thay cho đường kính d trong
công thức (4- 10):
ν
vR
R=Re (4 – 14)
Thí nghiệm cho biết:
Khi ReR < 580 thì trạng thái chảy tầng sẽ xảy ra.
Khi ReR > 580 thì trạng thái sẽ là chảy rối. Đại đa số dòng chảy trong ống,
kênh, sông, suối..v…v.. là chảy rối.