Giáo trình Vật lý 2 ThS. Trương Thành
32
CHƯƠNG IV
DAO ĐỘNG VÀ SÓNG CƠ
4.1. DAO ĐỘNG ĐIỀU HOÀ
4.1.1. DAO ĐỘNG ĐIỀU HOÀ
Dao động là chuyển động trong một không gian hẹp và xung quanh một
vị trí cân bằng, trong cuộc sống ta gặp nhiều các chuyển động dao động như:
sự đung đưa của cành lá, võng, sự dập dềnh của các vật nổi trên mặt nước
.v.v..
Dao động điều hoà là dao động mà độ lệch khỏi vị trí cân bằng của vật
là hàm của sin hay cosin.
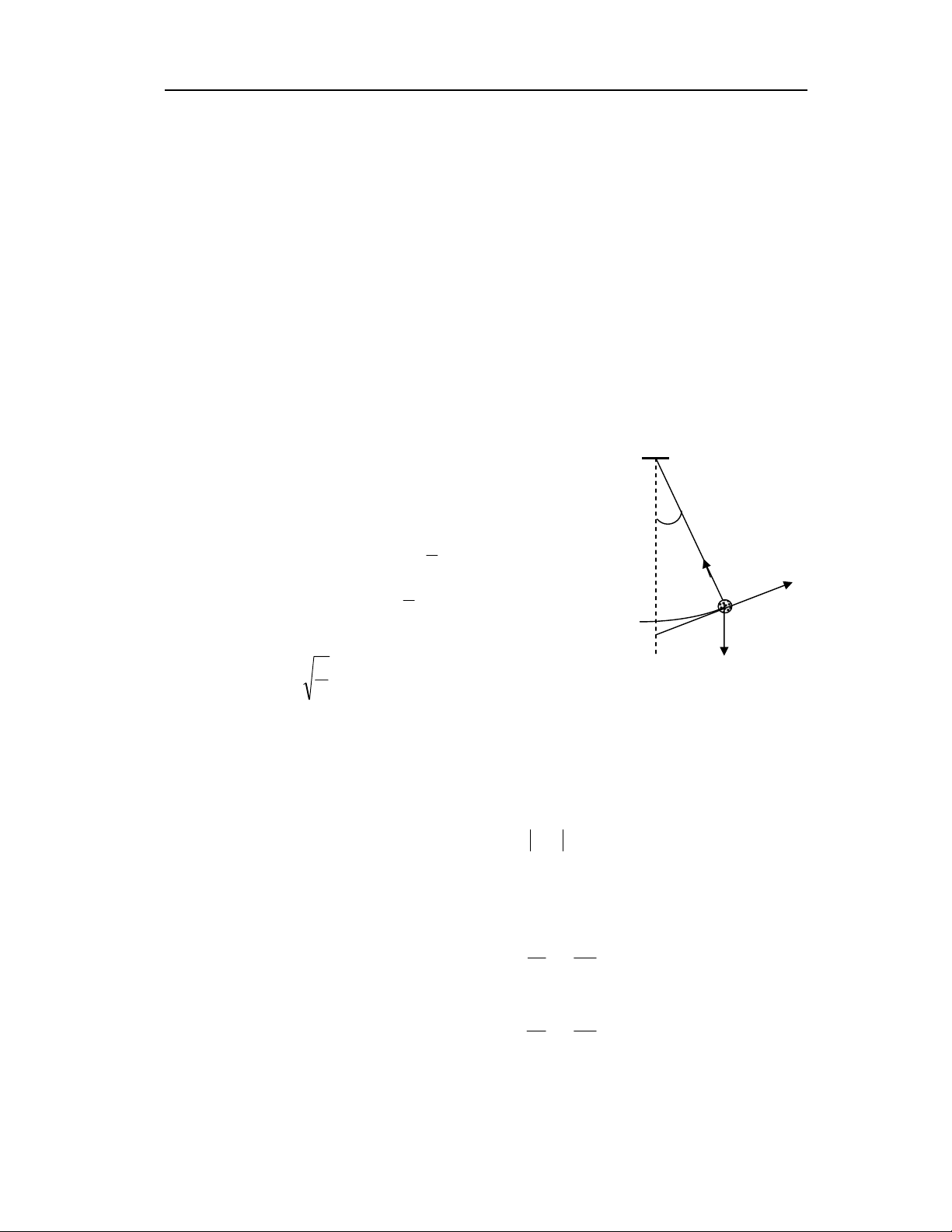
Dưới đây ta sẽ xét dao động một con lắc toán học (hay con lắc đơn)
trên hình IV-1. Tại vị trí bất kỳ con lắc chụi tác dụng của hai lực là trọng
lượng P
r
và sức căng dây T
r
phương trình chuyển động của con lắc là:
amTP
r
r
r
=+
Chiếu lên phương Ox phương trình còn lại:
''sin mxP
=
−
α
Do góc dao động bé nên:
l
x
=≈
αα
sin .
Dẫn đến: 0'' =+ l
x
mgmx
Hay 0'' 2
0=+ xx
ω
(a)
(trong đó l
g
=
0
ω
gọi là tần số góc của dao động).
Nghiệm của phương trình (a) có dạng:
)cos( 00
ϕ
ω
+
=
tAx (IV-1).
Đó là phương trình của dao động điều hoà của con lắc đơn, ta cũng sẽ
tìm được phương trình giống như vậy cho con lắc lò xo.
4.1.2. CÁC ĐẶC TRƯNG CỦA DAO ĐỘNG ĐIỀU HOÀ
- Biên độ của dao động: Max
xA =
0.
- Ly độ của dao động:
.
- Pha của dao động: )( 0
ϕ
ω
+
t
- Pha ban đầu của dao động:
ϕ
.
- Tần số của dao động:
π
ω
γ
2
10
0
0== T.
- Tần số góc của dao động:
ω
.
- Chu kỳ của dao động:
00
0
21
ω
π
γ
==T.
- Vận tốc của dao động: )sin(' 00
ϕ
ω
ω
+
−
=
=
tAxv
Hình IV-1
O
α
l
x
p
r
T
r
Giáo trình Vật lý 2 ThS. Trương Thành
33
- Gia tốc của dao động: )cos('' 0
2
0
ϕωω
+−= tAx .
- Công thức liên hệ giữa vận tốc và toạ độ:
1
2
0
2
0
2
2
0
2
=+ A
v
A
x
ω
Giáo trình Vật lý 2 ThS. Trương Thành
34
4.2. DAO ĐỘNG TẮT DẦN
4.2.1. DAO ĐỘNG TẮT DẦN
Dao động điều hoà là dao động lý tưởng, trong thực tế thì các dao động
tắt dần mới là phổ biến. Nguyên nhân của dao động tắt dần là do lực cản trong
đó có lực ma sát và sức cản của môi trường.
Thực tế đã chứng tỏ rằng với các vận tốc không quá lớn như máy bay
,ôtô, tàu thuỷ, tên lửa,.v.v..thì lực cản môi trường tỷ lệ với vận tốc:
vFC
r
r
µ
−=
(
µ
là hệ số cản của môi trường)
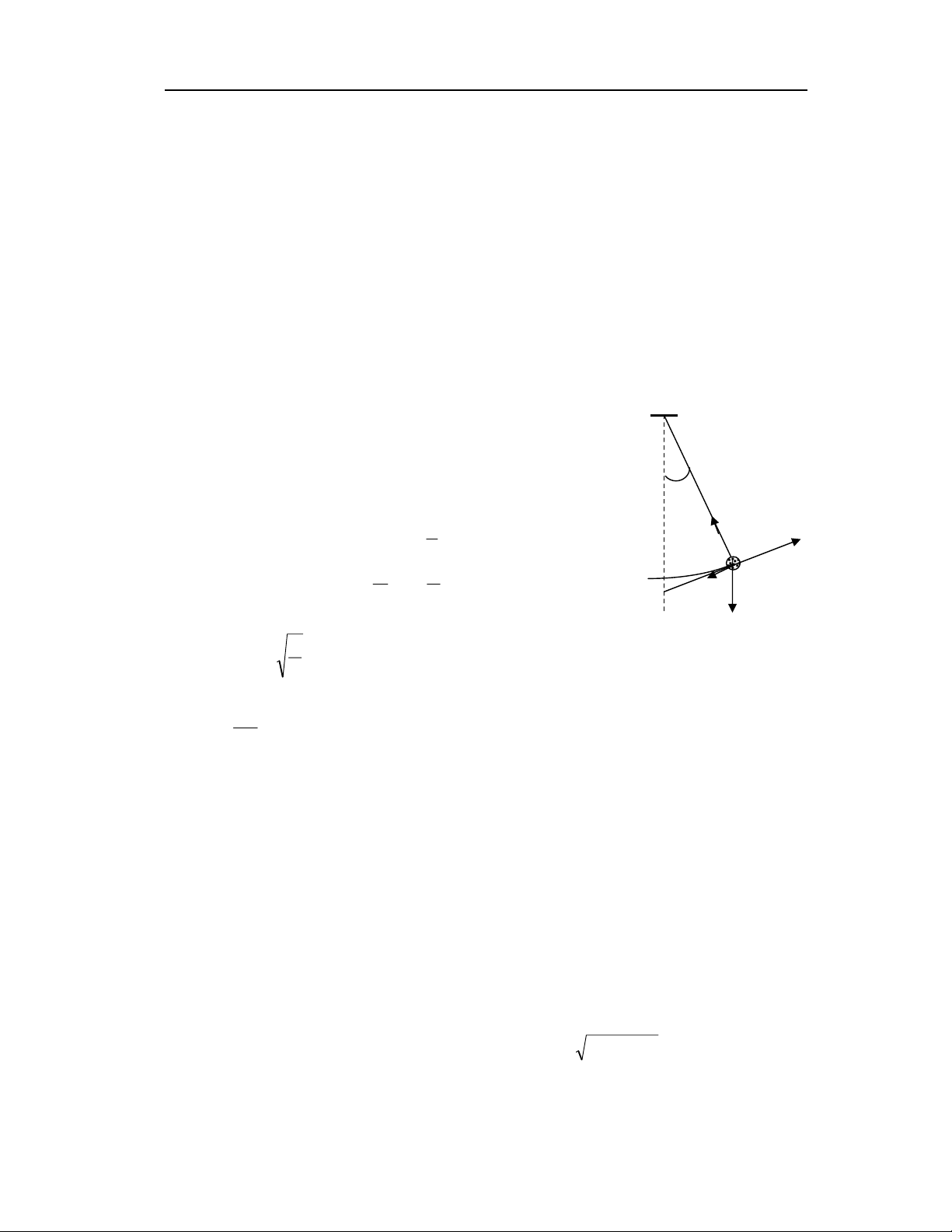
4.2.2. PHƯƠNG TRÌNH CỦA DAO ĐỘNG TẮT DẦN
Phương trình dao động tắt dần khác với dao động điều hoà ở chỗ có
thêm lực cản của môi trường:
amTPFC
r
r
r
r
=++
Chiếu lên phương Ox phương trình còn lại:
''sin' mxPx
=
−−
α
µ
Do góc dao động bé nên:
l
x
=≈
αα
sin .
Dẫn đến: 0''' =++ x
l
g
x
m
x
µ
.
Ta đặt:
- l
g
=
0
ω
và gọi là tần số góc của dao động
riêng.
-
β
µ
=
m2 là hệ số tắt dần.
Suy ra: 0'2'' 2
0=++ xxx
ωβ
(a)
Nghiệm của phương trình (a) có dạng:
)cos(
0
ϕω
β
+= −teAx t (IV-2).
Hay: )sin(
0
ϕω
β
+= −teAx t
Đó là phương trình của dao động tắt dần của con lắc đơn, ta cũng sẽ
tìm được phương trình giống như vậy cho con lắc lò xo, vấn đề khác giữa
chúng chỉ là tần số. Ta có nhận xét là ngoài những đại lượng quen thuộc đã
nói ở trên còn có thêm:
* Hệ số tắt dần
β
* Biên độđao động tắt dần là t
eA
β
−
0 giảm dần theo thời gian
* Tần số góc của dao động tắt dần 22
0
βωω
−=
C
F
r
Hình IV-2
O
α
l
x
p
r
T
r
Giáo trình Vật lý 2 ThS. Trương Thành
35
* Chu kỳ dao động tắt dần 22
0
22
βω
π
ω
π
−
==T
Sự tắt dần của dao động còn thể hiện ở chỗ:
∞→
=
t
x0lim .
* Để đặc trưng cho sự tắt dần người ta đưa ra khái niệm giảm lượng
loga với định nghĩa như sau:
Giảm lượng loga là ln của tỷ số giữa hai biên độ của dao động tại hai
thời điểm cách nhau một chu kỳ.
T
eA
eA
A
A
tt
t
Tt
t
βδ
β
β
=== +−
−
+
)(
)0(
0
)(
)( lnln (IV-3).
Giáo trình Vật lý 2 ThS. Trương Thành
36
4.3. DAO ĐỘNG CƯỠNG BỨC
4.3.1. DAO ĐỘNG CƯỠNG BỨC
Trên thực tế các dao động tự nó sẽ tắt dần theo thời gian, dao động đó
ta còn gọi là dao động riêng. Để duy trì dao động ta phải bù vào phần năng
lượng đã hao phí sau mỗi chu kỳ bằng cách tác dụng lên nó một lực tuần
hoàn:
)cos(
0tff Ω=
r
r
(IV-4).
Khi đó dao động được gọi là dao động cưỡng bức,
Ω
là tần số cưỡng
bức. 0
f
r là biên độ của lực cưỡng bức (trong trường hợp này ta đã chọn pha
ban đầu của lực cưỡng bức bằng 0).
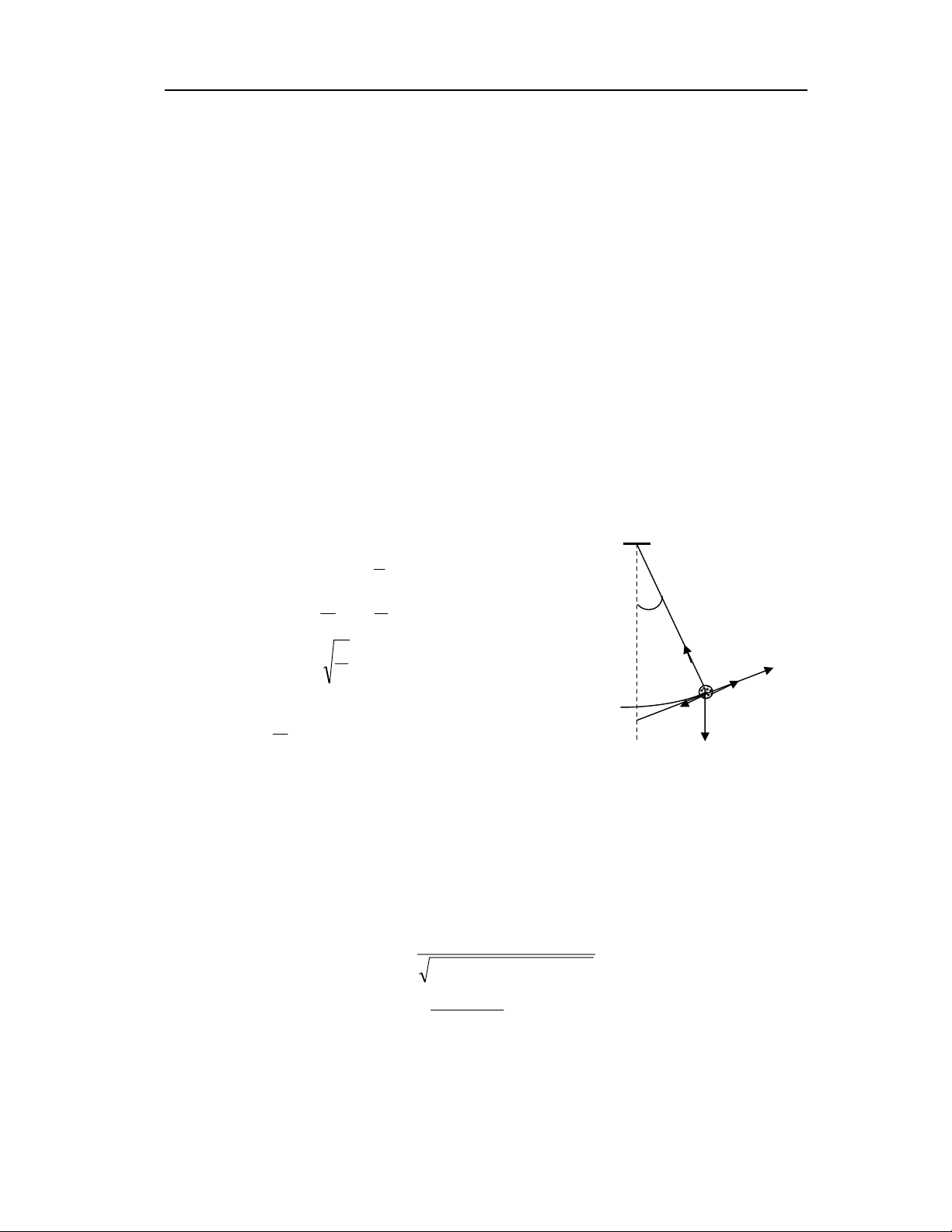
4.3.2. PHƯƠNG TRÌNH CỦA DAO ĐỘNG CƯỠNG BỨC
Phương trình dao động cưỡng bức khác với dao động tắt dần ở chỗ có
thêm lực cưỡng bức:
amTPFf C
r
r
r
r
r=+++
Chiếu lên phương Ox phương trình còn lại:
''sin'cos
0mxPxtf
=
−
−
Ω
α
µ
Trong đó do góc dao động bé nên:
l
x
=≈
αα
sin .
Dẫn đến: tfx
l
g
x
m
xΩ=++ cos''' 0
µ
.
Ta đặt: l
g
=
0
ω
gọi là tần số góc của dao
động riêng.
β
µ
2=
m,
β
là hệ số tắt dần.
Suy ra: tfxxx Ω=++ cos'2'' 0
2
0
ωβ
(a)
Nghiệm của phương trình (a) có dạng:
)cos(
ϕ
+
Ω
=
tAx (IV-5).
Đó là phương trình của dao động cưỡng bức của con lắc đơn, ta cũng
sẽ tìm được phương trình giống như vậy cho con lắc lò xo vấn đề khác giữa
chúng chỉ là tần số. Trong đó:
* Tần số cưỡng bức:
Ω
* Biên độ: 2222
0
0
4)( Ω+Ω−
=
βω
f
A (IV-6).
* Pha ban đầu
ϕ
: 22
0
2
Ω−
Ω
=
ω
β
ϕ
tg (IV-7).
* Ngoài ra ta có nhận xét khi tần số dao động riêng bằng tần số ngoại
lực kích thích thì biên độ dao động cực đại :
f
r
C
F
r
C
F
r
Hình IV-3
O
α
l
x
p
r
T
r