11
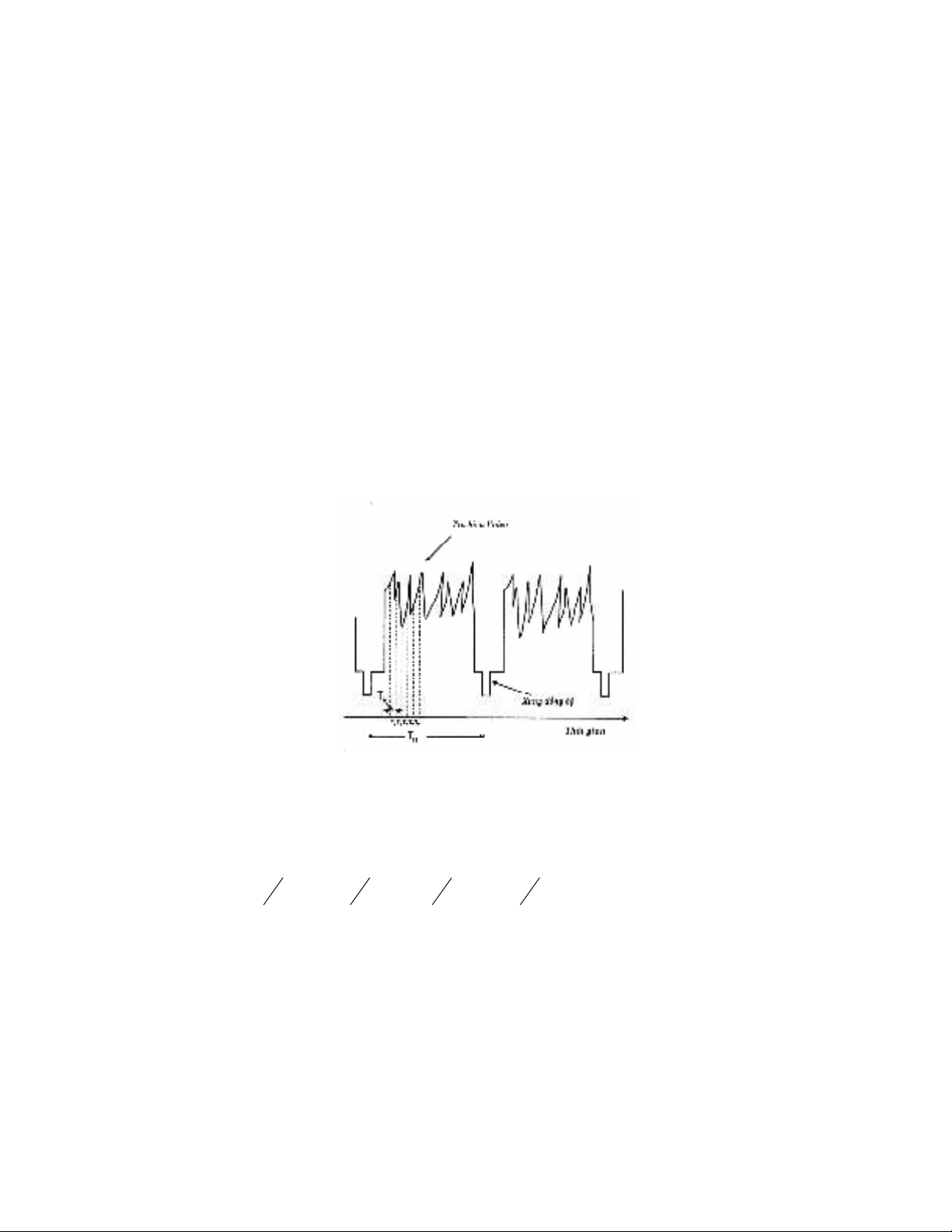
Hình 2.3 TV và TH cho lấy mẫu ảnh trên một ma trận camera CCD.
Hình 2.4 TV và TH cho một ảnh quét xen kẽ.
Hàm H(1,2) xác định trên toàn bộ miền
1 2 và là hàm tuần hoàn trong miền tần số
với chu kì tuần hoàn là 2 đối với 1 và 2. H(u,v) xác định trên
miền
HHVV TvTTuT 2
1
2
1
2
1
2
1 và là hàm tuần hoàn với
chu kì 1/TV và 1/TH cho u và v. Có thể chiếu H(
1,
2) hoặc H(u, v)
lên miền chuẩn hoá, ở đây /1, /2
11, bằng cách đặt /1=1/;
/2=2/ hoặc /1=2uTV; /2=2vTh . /1 và /2 gọi là tần số chuẩn
hoá, hàm H(
/
1,
/
2 ) có thể viết lại
12
)(
2121
2211
1 2
),(),( kkj
k k
ekkhH
(2.13)
Nếu chúng ta hạn chế h(n1,n1) chỉ lấy các giá trị thực thì đáp ứng
tần số thoả mãn:
),(),( 2121
jjjj eeHeeH
(2.14)
H* = liên hợp phức của H. Điều này dẫn đến H(
1,
2) đối xứng
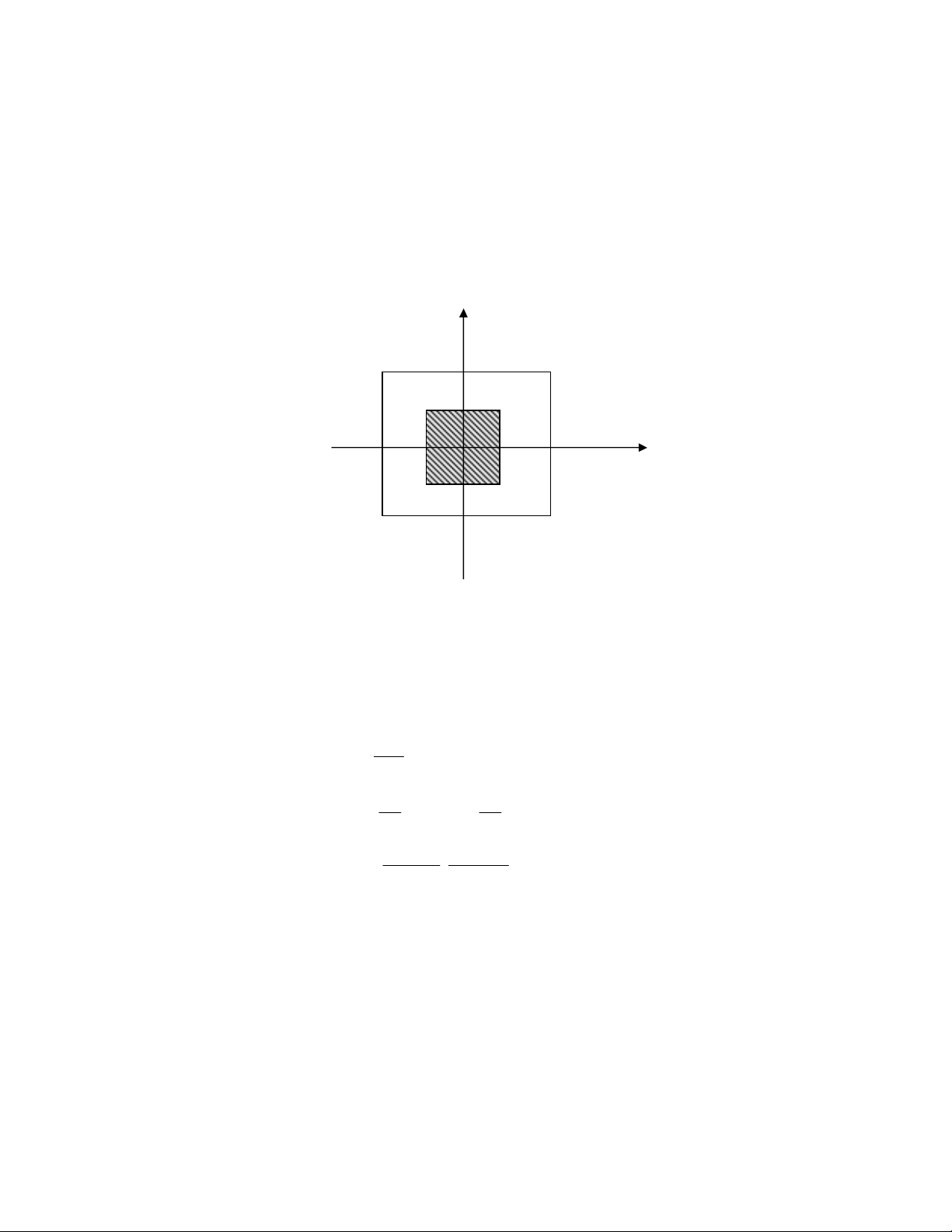
(Hình 2.5).
Hình 2.5 Đối xứng tâm.
Chú ý rằng nếu x(n1,n2) =
(n1,n2), thì biểu thức (2.2) trở thành
y(n1,n2) = h(n1,n2). Vì lý do này mà h(n1,n2) được gọi là đáp ứng
xung, hoặc là đáp ứng biên độ, của hệ thống 2-D.
Bài tập 2.1 Tính biểu thức đáp ứng tần số của một hệ thống với
đáp ứng xung cho bởi
0.0
5.0
125.0
125.0
125.0
),( 21 nnh
Chứng minh rằng công thức tính đáp ứng tần số có thể tách được.
A
B
B
*
A
*
1
2
l¹ i cßn hî ptrêng c¸c
0
1,0
0,1
1,1
21
21
21
21
nn
nn
nn
nn
13
2.5 Tính đáp ứng xung từ đáp ứng tần số
Đáp ứng tần số của h(n1,n2) được cho bởi :
1 2
)(
2121
2211
),(),H(
n n
nnj
ennh
(2.15)
Xét tích phân
21
)(
21
2
2211
),(
4
1ddeH kkj
(2.16)
Thay biểu thức (2.15) vào biểu thức (2.16) chúng ta được
21
)()(
21
2
1 2
22112211 )),((
4
1
ddeennh
n n
kkjnnj
Và có thể viết thành
2
)(
1
)(
21
2122111
1 2 2
1
2
1
),(
dedennh knjknj
n n
Và biến đổi thành
),()()(),( 21221121
1 2
kkhknknnnh
n n
Điều này có nghĩa là đáp ứng xung có thể tính từ đáp ứng tần số
qua mối quan hệ:
h(n1,n2) =
21
)(
21
2
2211
),(
4
1ddeH nnj
(2.17)
Nếu đáp ứng tần số được cho dưới dạng hàm của u,v (vòng/đơn
vị), thì biểu thức (2.17) có thể viết thành
vdduvuHTTnnh
V
V
H
H
HV
T
T
T
T
nvTnuTj
HV e
2
1
2
1
2
1
2
1
_
)(2
21
211
),(),(
(2.18)
Hoặc cho tần số chuẩn hoá:
1
1
2
1
1
1
)(
2121
2211
),(
4
1
),(
ddeHnnh nnj (2.19)
14
Ví dụ 2.3 Cho đáp ứng tần số
0
||,|| 1
),( 21
21 l¹i cßn hîp trêng c¸c
ba
H
(xem hình 2.10), hãy tính đáp ứng xung.
Hình 2.10 Ví dụ 2.3.
Giải Từ phương trình (2.17) chúng ta có thể viết :
2
2
1
1
21
21
)(
2
21
)sin(bn
.
)sin(an
=
2
1
2
1
=
4
1
),(
2211
2211
nn
dede
ddennh
b
b
nj
a
a
nj
a
a
b
b
nnj
Bởi vì đáp ứng tần số là hàm tách được của hai biến 1
và 2
nên
đáp ứng xung cũng là một hàm hai biến tách được. Khái niệm “tách
được” ở đây nghĩa là có thể phân tích h(n1,n2) = f1(n1).f2(n2).
Ví dụ 2.4 Tìm đáp ứng xung của một bộ lọc thông thấp đối xứng
vòng tròn lý tưởng được mô tả như sau (xem hình 2.11 và 2.12):
1
a
-
a
b
b
-
-
2
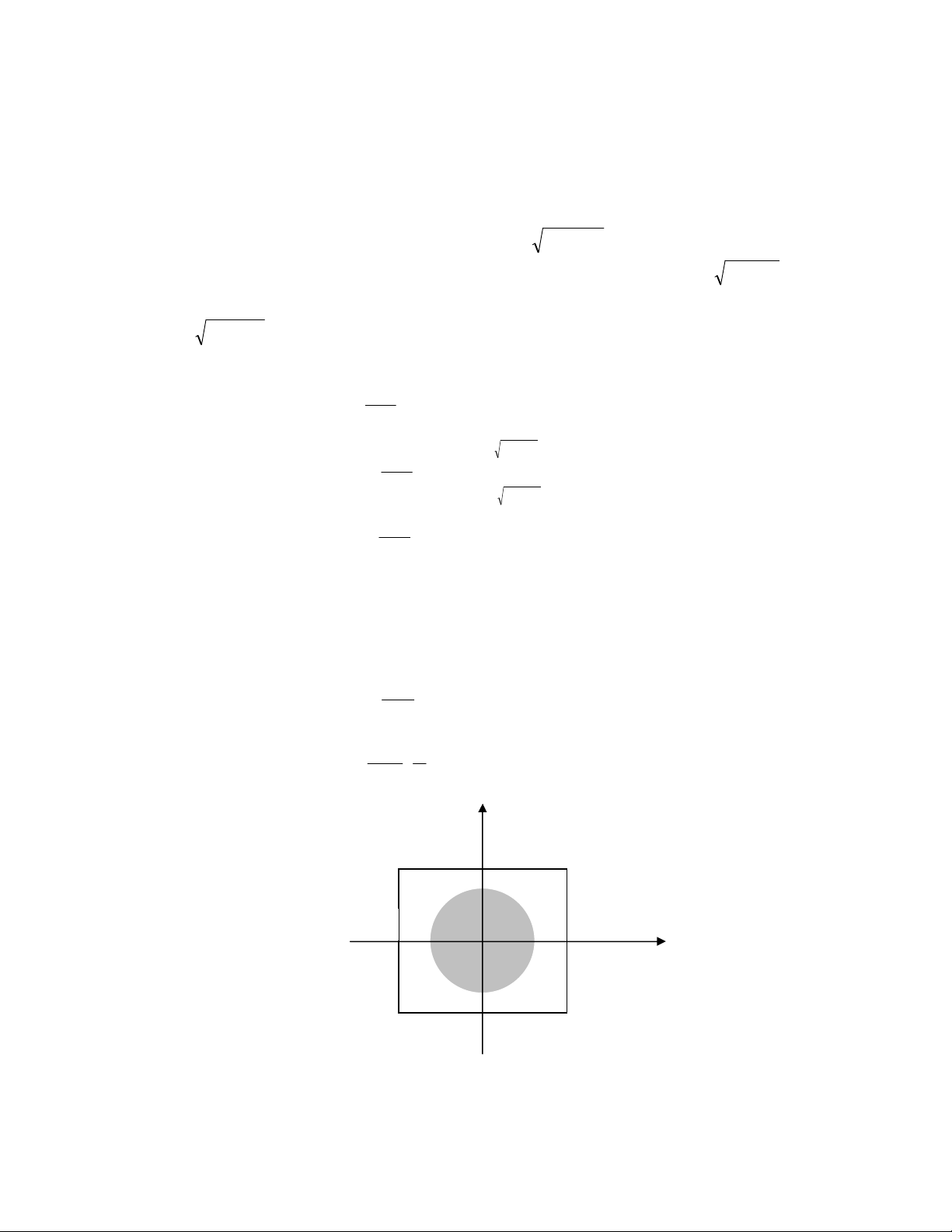
15
l¹i cßn hîp trêng c¸c 0
1
),(
22
2
2
1
21
R
eeH jj
Giải Có thể dễ dàng thấy nếu ),( 21
Hlà một hàm đối xứng vòng
tròn lý tưởng, cụ thể là )(),( 2
2
2
121
HH thì ),( 21 nnh cũng là
một hàm tuần hoàn đối xứng vòng tròn, tức là h n n h n n( , ) ( )
1 2 1
2
2
2
.
Vì vậy cách dễ dàng nhất để tìm ),( 21 nnh là tìm h(n1, 0) và hàm
2
2
2
1+nn theo n1. Chúng ta rút ra )0,( 1
nh từ:
A
nj ddenh 21
2
1
11
4
1
)0,(
e
4
1
=
R
R-
j
2
1
2
1
21
2
1
)cos(2
4
1
)0,(
1
2
2
2
2
2
11
dR
ddenh
n
R
R
R
R
nj
Ta có )sin(
1
R
dRd )cos(
1
dcos2
4
1
)0,(
/2
/2-
sin
2
2
11
jRn
eRnh
hoặc
deRn
n
R
nh jRn
2/
2/
sin2
1
1
11
cos)(
1
2
)0,(
1
R
-
R
-
-
2