TRAÀN SÓ TUØNG
---- ›š & ›š ----
TÀI LIỆU ÔN THI ĐẠI HỌC – CAO ĐẲNG
Naêm 2012
Trần Sĩ Tùng Hệ phương trình nhiều ẩn
Trang 1
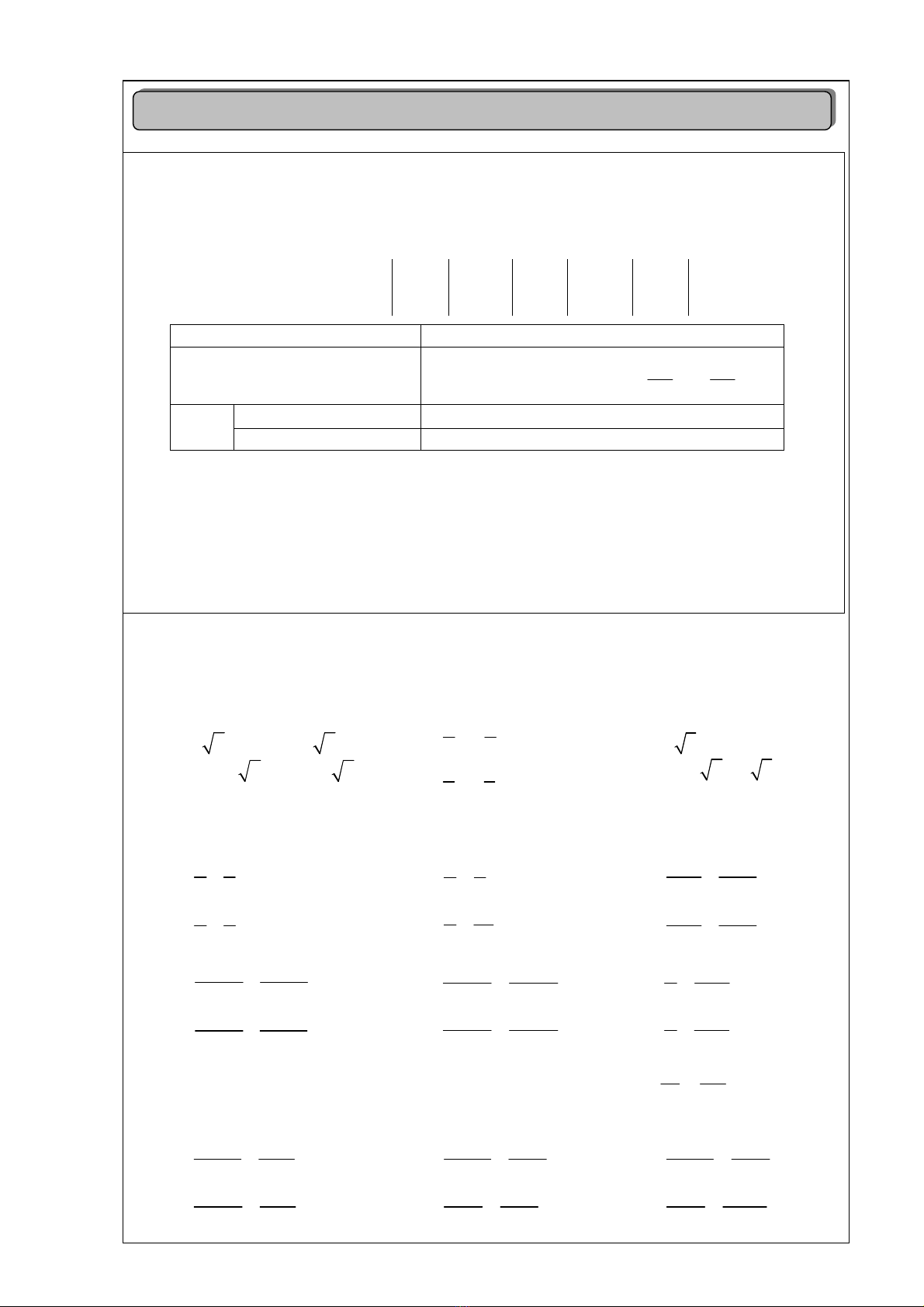
1. Hệ phương trình bậc nhất hai ẩn
axbyc abab
axbyc
2222
111 1122
222
(0,0)
ì+=
+¹+¹
í+=
î
Giải và biện luận:
– Tính các định thức:
ab
D
ab
11
22
=, x
cb
D
cb
=, y
ac
D
ac
11
22
=.
Chú ý: Để giải hệ phương trình bậc nhất hai ẩn ta có thể dùng các cách giải đã biết như:
phương pháp thế, phương pháp cộng đại số.
2. Hệ phương trình bậc nhất nhiều ẩn
Nguyên tắc chung để giải các hệ phương trình nhiều ẩn là khử bớt ẩn để đưa về các
phương trình hay hệ phương trình có số ẩn ít hơn. Để khử bớt ẩn, ta cũng có thể dùng các
phương pháp cộng đại số, phương pháp thế như đối với hệ phương trình bậc nhất hai ẩn.
Bài 1. Giải các hệ phương trình sau:
a) xy
xy
543
798
ì
-=
í
-=
î b) xy
xy
211
548
ì
+=
í
-=
î c) xy
xy
31
625
ì
-=
í
-=
î
d)
(
)
( )
xy
xy
2121
22122
ì
ï
++=-
í--=
ï
î
e)
xy
xy
32
16
43
53
11
25
ì
+=
ï
í
ï
-=
î
f) xy
y
31
5x23
ì
ï-=
í+=
ï
î
ĐS:
Bài 2. Giải các hệ phương trình sau:
a) xy
xy
18
18
54
51
ì
-=
ï
ï
í
ï
+=
ï
î
b) xy
xy
65
3
910
1
ì
+=
ï
ï
í
ï
-=
ï
î
c) xy
xy
101
1
12
253
2
12
ì
+=
ï
ï-+
í
ï
+=
ï-+
î
d) xyxy
xyxy
2732
7
23
4548
1
23
ì
+=
ï
ï-+
í
ï
-=-
ï-+
î
e) xyxy
xyxy
62
3
22
34
1
22
ì
+=
ï
ï-+
í
ï
+=-
-+
ï
î
f) xy
xy
41
3
1
22
4
1
ì
+=
ï
ï-
í
ï
-=
-
ï
î
ĐS: a) b) c) d) e)
387
;
70140
æö
-
ç÷
èø
f)
Bài 3. Giải các hệ phương trình sau:
a)
xy
yx
xy
yx
632
5
11
424
2
11
ì
-
-=
ï
ï-+
í
-
ï
-=
-+
ï
î
b)
xx
yy
xx
yy
36
1
12
23
7
12
ì
-
-=
ï
ï+-
í
-
ï
+=
+-
ï
î
c)
xy
xy
xy
xy
237
5
23
131
5
23
ì
-+
+=
ï
ï-+
í
++
ï
+=
-+
ï
î
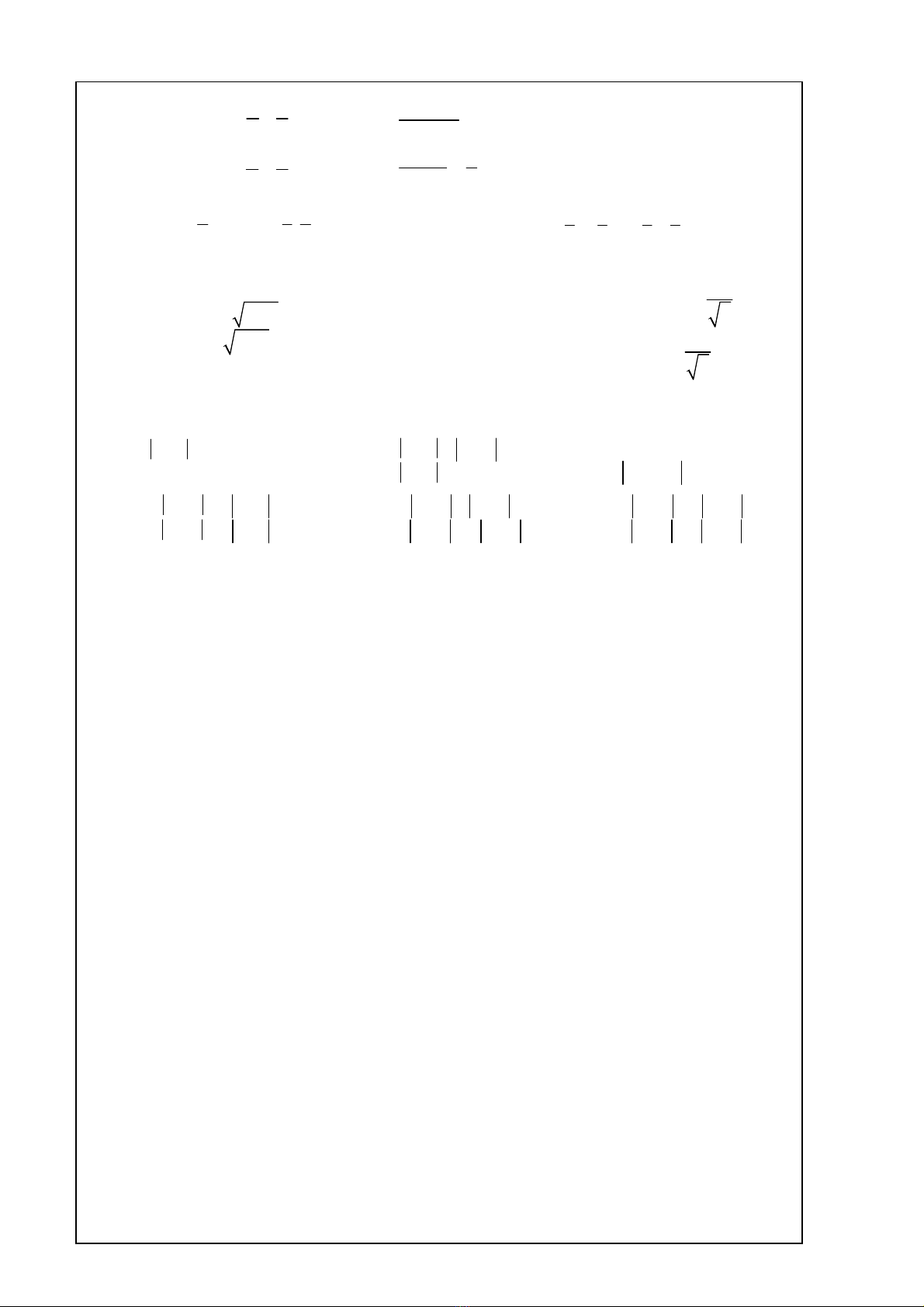
I. HỆ PHƯƠNG TRÌNH BẬC NHẤT NHIỀU ẨN
Xét D Kết quả
D
¹
0 Hệ có nghiệm duy nhất
y
x
D
D
xy
DD
;
æö
==
ç÷
èø
Dx
¹
0 hoặc Dy
¹
0 Hệ vô nghiệm
D = 0
Dx = Dy = 0 Hệ có vô số nghiệm
Hệ phương trình nhiều ẩn Trần Sĩ Tùng
Trang 2
d)
xy xy
xy xy
11
3()26
11
3()24
ìæö
++-=
ïç÷
ïèø
íæö
ï
-++=
ç÷
ïèø
î
e)
xy
xy
xy
yx
3()
7
55
3
ì+
=-
ï
ï-
í-
ï=
-
ï
î
f)
ĐS: a)
1
0;
2
æö
ç÷
èø
b)
57
;
84
æö
ç÷
èø
c) d)
( )
2222
1;1,1;,;1,;
3333
æöæöæö
--
ç÷ç÷ç÷
èøèøèø
Bài 4. Giải các hệ phương trình sau:
a) xxy
xxy
2
2
2213
214
ì
ï
+--=
í
++-=
ï
î
b) xy
xy
2
2
31
2715
ì
ï+=
í
-=
ï
î c)
x
y
x
y
2
2
5
2(4)2
2
44
ì
-+=
ï
ï
í
ï-+=
ï
î
ĐS: a)
(1;2),(2;2)
-
b)
(
)
2;1
±-
c)
Bài 5. Giải các hệ phương trình sau:
a) xy
xy
10
21
ì
-+=
í-=
î b) xy
xy
121
13
ì
-+-=
í-+=
î c) xy
xy
22
231
ì+=
í
-=
î
d) xy
xy
26315
56411
ì
-++=
í
--+=
î e) xyxy
xyxy
29
3217
ì+--=
í
++-=
î f) xyxy
xyxy
438
356
ì
++-=
í
+--=
î
ĐS:
Bài 6. Giải và biện luận các hệ phương trình sau:
a) mxmym
xmy
(1)1
22
ì
+-=+
í+=
î b) mxmy
mxmy
(2)5
(2)(1)2
ì
+-=
í
+++=
î c) mxym
mxym
(1)231
(2)1
ì
-+=-
í+-=-
î
Bài 7. Trong các hệ phương trình sau hãy:
i) Giải và biện luận. ii) Tìm m Î Z để hệ có nghiệm duy nhất là nghiệm nguyên.
a) mxym
mxymm
22
(1)21
2
ì+-=-
í-=+
î b) mxy
xmym
1
4(1)4
ì-=
í
++=
î c) mxy
xmym
33
210
ì+-=
í
+-+=
î
Bài 8. Trong các hệ phương trình sau hãy:
i) Giải và biện luận.
ii) Khi hệ có nghiệm (x; y), tìm hệ thức giữa x, y độc lập đối với m.
a) mxym
xmym
21
225
ì
+=+
í
+=+
î b) mxmy
mxmy
6(2)3
(1)2
ì
+-=
í
--=
î c) mxmym
xmy
(1)1
22
ì
+-=+
í+=
î
Bài 9. Trong các hệ phương trình sau:
i) Tìm số nguyên m để hệ có nghiệm duy nhất là nghiệm nguyên.
ii) Khi hệ có nghiệm (x, y) , tìm hệ thức giữa x, y độc lập với m.
a) xy
yxm
25
2105
ì+=
í
-=+
î b) mxym
xmym
3
ì+=
í
+=+
î c)
xym
xym
24
233
ì-=-
í
+=+
î
Bài 10. Giải và biện luận các hệ phương trình sau:
a)
axyb
xy
325
ì+=
í
+=-
î b)
yaxb
xy
234
ì
-=
í
-=
î c)
axyab
xya2
ì
+=+
í+=
î
Bài 11. Giải các hệ phương trình sau:
a)
xyz
xyz
xyz
31
225
230
ì
+-=
ï
-+=
í
ï
--=
î
b)
xyz
xyz
xyz
328
26
36
ì
++=
ï
++=
í
ï
++=
î
c)
xyz
xyz
xyz
327
2438
35
ì
-+=-
ï
-++=
í
ï+-=
î
ĐS:
Trần Sĩ Tùng Hệ phương trình nhiều ẩn
Trang 3
1. Hệ gồm 1 phương trình bậc nhất và 1 phương trình bậc hai
· Từ phương trình bậc nhất rút một ẩn theo ẩn kia.
· Thế vào phương trình bậc hai để đưa về phương trình bậc hai một ẩn.
· Số nghiệm của hệ tuỳ theo số nghiệm của phương trình bậc hai này.
2. Hệ đối xứng loại 1
Hệ có dạng: (I) fxy
gxy
(,)0
(,)0
ì
=
í
=
î (với f(x, y) = f(y, x) và g(x, y) = g(y, x)).
(Có nghĩa là khi ta hoán vị giữa x và y thì f(x, y) và g(x, y) không thay đổi).
· Đặt S = x + y, P = xy.
· Đưa hệ phương trình (I) về hệ (II) với các ẩn là S và P.
· Giải hệ (II) ta tìm được S và P.
· Tìm nghiệm (x, y) bằng cách giải phương trình: XSXP
2
0
-+=
.
3. Hệ đối xứng loại 2
Hệ có dạng: (I) fxy
fyx
(,)0(1)
(,)0(2)
ì=
í=
î
(Có nghĩa là khi hoán vị giữa x và y thì (1) biến thành (2) và ngược lại).
· Trừ (1) và (2) vế theo vế ta được:
(I) Û fxyfyx
fxy
(,)(,)0(3)
(,)0(1)
ì-=
í=
î
· Biến đổi (3) về phương trình tích:
(3) Û
xygxy
().(,)0
-=
Û xy
gxy
(,)0
é=
ê
=
ë.
· Như vậy: (I) Û
fxy
xy
fxy
gxy
(,)0
(,)0
(,)0
éì
=
í
ê=
î
êì
=
êí
ê
=
î
ë
.
· Giải các hệ trên ta tìm được nghiệm của hệ (I).
Chú ý: Với các hệ phương trình đối xứng, nếu hệ có nghiệm
xy
00
(;)
thì
yx
00
(;)
cũng là nghiệm của hệ. Do đó nếu hệ có nghiệm duy nhất thì
xy
00
=
.
4. Hệ đẳng cấp bậc hai
Hệ có dạng: (I)
axbxycyd
axbxycyd
22
1111
22
2222
ì++=
ï
í
++=
ï
î
.
· Giải hệ khi x = 0 (hoặc y = 0).
· Khi x
¹
0, đặt
ykx
=
. Thế vào hệ (I) ta được hệ theo k và x. Khử x ta tìm được phương
trình bậc hai theo k. Giải phương trình này ta tìm được k, từ đó tìm được (x; y).
II. HỆ PHƯƠNG TRÌNH BẬC HAI HAI ẨN
Hệ phương trình nhiều ẩn Trần Sĩ Tùng
Trang 4
VẤN ĐỀ 1: Hệ gồm 1 phương trình bậc nhất và 1 phương trình bậc hai
Bài 1. Giải các hệ phương trình sau:
a) xy
xy
22
48
24
ì
+=
í
+=
î b) xxy
xy
2
24
231
ì
-=
í
-=
î c) xy
xy
2
()49
3484
ì
-=
í+=
î
d) xxyyxy
xy
22
26
23
ì
++--=
í-=
î e) xy
xyxy
3410
3()9
ì-+=
í
=+-
î f) xy
xyxy
232
60
ì+=
í
+++=
î
g)
yxx
xy
24
250
ì+=
í
+-=
î h) xy
xyy
22
235
324
ì+=
í
-+=
î i) xy
xxyy
22
25
7
ì-=
í
++=
î
ĐS:
Bài 2. Giải các hệ phương trình sau:
a) xy
yxxy
22
270
2240
ì--=
í
-+++=
î b) xy
xxyxy
2
496
3630
ì+=
í
+-+=
î c) xxy
xxy
2
2
210
122100
ì
ï+++=
í
+++=
ï
î
d) xyxy
xyyx
2
(21)(22)0
310
ì
++++=
í+++=
î e) xyxy
xy
(232)(53)0
31
ì
+---=
í-=
î f)
xy
xy
22
115
2312
ì+=
í+=
î
ĐS:
Bài 3. Giải các hệ phương trình sau:
a)
xxyyyy
xy
22
237121
10
ì
-+=+-
í-+=
î b) xyxy
xy
22
620
80
ì
+++=
í++=
î
c) xyxyxy
xy
22
94642401350
3290
ì
+++-+=
í-+=
î d) xxyx
xy
2
10
25
ì
++=
í-=-
î
d) xyxyxy
xy
22
79125350
231
ì
+-+++=
í-=
î e) xxyyxy
xy
22
32360
23
ì
-+++-=
í-=
î
ĐS:
Bài 4. Giải các hệ phương trình sau:
a)
xyxy
xy
xy
3
2
12
4
ì
+-
-=
ï
í-
ï-=
î
b) xy
xy
22
111
323
111
4
94
ì
-=
ï
ï
í
ï
-=
ï
î
c) xy
xy
22
111
13
111
4
(1)
ì+=
ï
+
ï
í
ï
-=
ï+
î
d) xyxy
xy
22
()4()1170
25
ì
+++-=
í-=
î e) xy
xy
33
1
7
ì-=
í
-=
î f) xyxy
xy
22
()()45
5
ì
--=
í+=
î
ĐS:
Bài 5. Giải và biện luận các hệ phương trình sau:
a) xy
xym
22
6
ì+=
í
+=
î b) xym
xyx
22
22
ì+=
í
-+=
î c) xy
xym
22
321
ì
-=
í
+=
î
ĐS: