Đề tài tốt nghiệp: "Khảo sát phương pháp bình sai lưới trắc địa tự do và ứng dụng trong xử lý lưới thi công công trình"

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

môc lôc

Trang

Môc lôc ............................................................................................................................................ 1

Më ®Çu ............................................................................................................................................ 2

Ch¬ng 1 – Tæng quan vÒ líi khèng chÕ tr¾c ®Þa c«ng

tr×nh ....................................................................................................................... 3 1.1 Mét sè ®Æc ®iÓm cña líi khèng chÕ tr¾c ®Þa c«ng tr×nh ............................ 3

1.2 Nguyªn t¾c íc tÝnh líi tr¾c ®Þa c«ng tr×nh ..................................................... 8

1.3 Lùa chän hÖ to¹ ®é vµ mÆt chiÕu cho líi tr¾c ®Þa c«ng tr×nh .............. 13

1.4 TÝnh chuyÓn to¹ ®é .......................................................................................................... 16

1.5 Líi khèng chÕ thi c«ng c«ng tr×nh ..................................................................... 22

Ch¬ng 2 – Kh¶o s¸t ph¬ng ph¸p b×nh sai líi tù do ........... 28

2.1 Kh¸i niÖm chung vÒ líi tr¾c ®Þa tù do .............................................................. 28

2.2 §Þnh vÞ líi ......................................................................................................................... 32

2.3 Mét sè tÝnh chÊt c¬ b¶n cña kÕt qu¶ b×nh sai líi tù do ........................... 33

2.4 NhËn xÐt vÒ b×nh sai líi tù do ............................................................................... 37

Ch¬ng 3 – øng dông ph¬ng ph¸p b×nh sai líi tr¾c ®Þa

tù do ®Ó xö lý líi thi c«ng c«ng tr×nh ............. 39

3.1 ThuËt to¸n xö lý sè liÖu líi thi c«ng .................................................................. 39

3.2 LËp ch¬ng tr×nh b×nh sai ........................................................................................... 57

3.3 TÝnh to¸n thùc nghiÖm .................................................................................................. 62

KÕt luËn ........................................................................................................................................... 69

phô lôc ............................................................................................................................................. 70

Cao B¸ H¹

-1 -

Líp Tr¾c ®ÞaB-K48

Tµi liÖu tham kh¶o .......................................................................................................... 87

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

Më ®Çu

Trong nh÷ng n¨m gÇn ®©y c¸c c«ng tr×nh x©y dùng nh: c«ng tr×nh cÇu,

c«ng tr×nh c«ng nghiÖp - d©n dông, c«ng tr×nh thñy lîi, thñy ®iÖn… ®îc x©y

dùng ngµy cµng réng r·i. §Ó ®¸p øng ®îc c¸c yªu cÇu cña c«ng tr×nh th×

c«ng t¸c tr¾c ®Þa ®ãng vai trß quan träng ngay tõ giai ®o¹n kh¶o s¸t, thiÕt kÕ,

thi c«ng c«ng tr×nh ®Õn khi c«ng tr×nh b¾t ®Çu ®i vµo sö dông vµ æn ®Þnh.

C¸c m¹ng líi tr¾c ®Þa c«ng tr×nh thêng cã tÝnh ®Æc thï cao, v× vËy

cïng víi viÖc ®o ®¹c chÝnh x¸c (lùa chän dông cô m¸y mãc vµ ph¬ng ph¸p

®o) th× viÖc nghiªn cøu ph¬ng ph¸p tÝnh to¸n, quy tr×nh xö lý sè liÖu mét

c¸ch hîp lý, phï hîp víi ®Æc ®iÓm vµ b¶n chÊt cña líi tr¾c ®Þa c«ng tr×nh lµ

rÊt cÇn thiÕt.

§îc sù híng dÉn cña thÇy gi¸o TS. NguyÔn Quang Phóc t«i ®· lùa

chän ®Ò tµi tèt nghiÖp: “Kh¶o s¸t ph¬ng ph¸p b×nh sai líi tr¾c ®Þa tù do vµ

øng dông trong xö lý líi thi c«ng c«ng tr×nh”

Trong ®Ò tµi chóng t«i ®· ®Æt ra vµ kh¶o s¸t, nghiªn cøu c¸c néi dung

Ch¬ng 1: Tæng quan vÒ líi khèng chÕ trong tr¾c ®Þa c«ng tr×nh.

Ch¬ng 2: Kh¶o s¸t ph¬ng ph¸p b×nh sai líi tù do.

Ch¬ng 3: øng dông ph¬ng ph¸p b×nh sai líi tr¾c ®Þa tù do ®Ó xö lý líi thi

c«ng c«ng tr×nh.

KÕt luËn.

Hµ Néi, th¸ng 6 - 2006

Sinh viªn

Cao B¸ H¹

-2 -

Líp Tr¾c ®ÞaB-K48

Cao B¸ H¹

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

Ch¬ng 1

Tæng quan vÒ líi khèng chÕ tr¾c ®Þa c«ng tr×nh

1.1. Mét sè ®Æc ®iÓm cña líi khèng chÕ tr¾c ®Þa c«ng tr×nh

1.1.1. Líi khèng chÕ mÆt b»ng

Líi khèng chÕ ®îc lËp trªn khu vùc x©y dùng c«ng tr×nh c«ng nghiÖp, thµnh phè, khu vùc x©y dùng cÇu c¶ng, ®êng hÇm… lµ c¬ së tr¾c ®Þa phôc vô cho kh¶o s¸t thiÕt kÕ, thi c«ng x©y dùng vµ cho khai th¸c sö dông c«ng tr×nh.

Theo môc ®Ých thµnh lËp líi tr¾c ®Þa c«ng tr×nh cã thÓ ®îc ph©n thµnh 3 nhãm: Líi kh¶o s¸t c«ng tr×nh, líi thi c«ng c«ng tr×nh, líi quan tr¾c chuyÓn dÞch vµ biÕn d¹ng c«ng tr×nh.

Trong giai ®o¹n kh¶o s¸t , ngêi ta ph¶i nghiªn cøu tæng hîp c¸c ®iÒu kiÖn tù nhiªn cña vïng x©y dùng, thu thËp c¸c sè liÖu vÒ ®Þa h×nh, ®Þa m¹o, ®Þa chÊt c«ng tr×nh, ®Þa chÊt thñy v¨n, khÝ tîng,…®Ó cã gi¶i ph¸p kü thuËt hîp lý trong thiÕt kÕ x©y dùng c«ng tr×nh. §Ò xuÊt c¸c yªu cÇu vµ tiÕn hµnh thµnh lËp líi khèng chÕ tr¾c ®Þa khu vùc, ®o vÏ b¶n ®å ®Þa h×nh tØ lÖ trung b×nh, ®o vÏ mÆt c¾t ®Þa h×nh theo c¸c tuyÕn c«ng tr×nh, phôc vô cho giai ®o¹n thiÕt kÕ. ë giai ®o¹n thiÕt kÕ cÇn lËp b¶n ®å ®Þa h×nh, mÆt c¾t tû lÖ lín ®Ó thiÕt kÕ chi tiÕt. ChuÈn bÞ ph¬ng ¸n tr¾c ®Þa ®Ó chuyÓn thiÕt kÕ ra thùc ®Þa.

Trong giai ®o¹n thi c«ng, ph¶i tiÕn hµnh c«ng t¸c x©y dùng líi c¬ së tr¾c ®Þa phôc vô c¾m c«ng tr×nh, chuyÓn thiÕt kÕ ra thùc ®Þa ®óng vÞ trÝ, kÝch thíc ®· thiÕt kÕ. MÆt kh¸c ph¶i theo dâi thi c«ng hµng ngµy ®Ó ®¶m b¶o c¸c c«ng tr×nh cã kÕt cÊu ®óng thiÕt kÕ. Sau khi hoµn thµnh c«ng tr×nh cÇn ®o vÏ hoµn c«ng ®Ó kiÓm tra vÞ trÝ, kÝch thíc c«ng tr×nh ®· x©y dùng.

C«ng t¸c tr¾c ®Þa phôc vô quan tr¾c biÕn d¹ng c«ng tr×nh gåm ®o ®é lón

nÒn mãng, x¸c ®Þnh ®é xª dÞch vÞ trÝ mÆt b»ng vµ ®é nghiªng cña c«ng tr×nh.

ë níc ta líi tr¾c ®Þa c«ng tr×nh lµ mét bé phËn cña hÖ to¹ ®é quèc gia

Cao B¸ H¹

-3 -

Líp Tr¾c ®ÞaB-K48

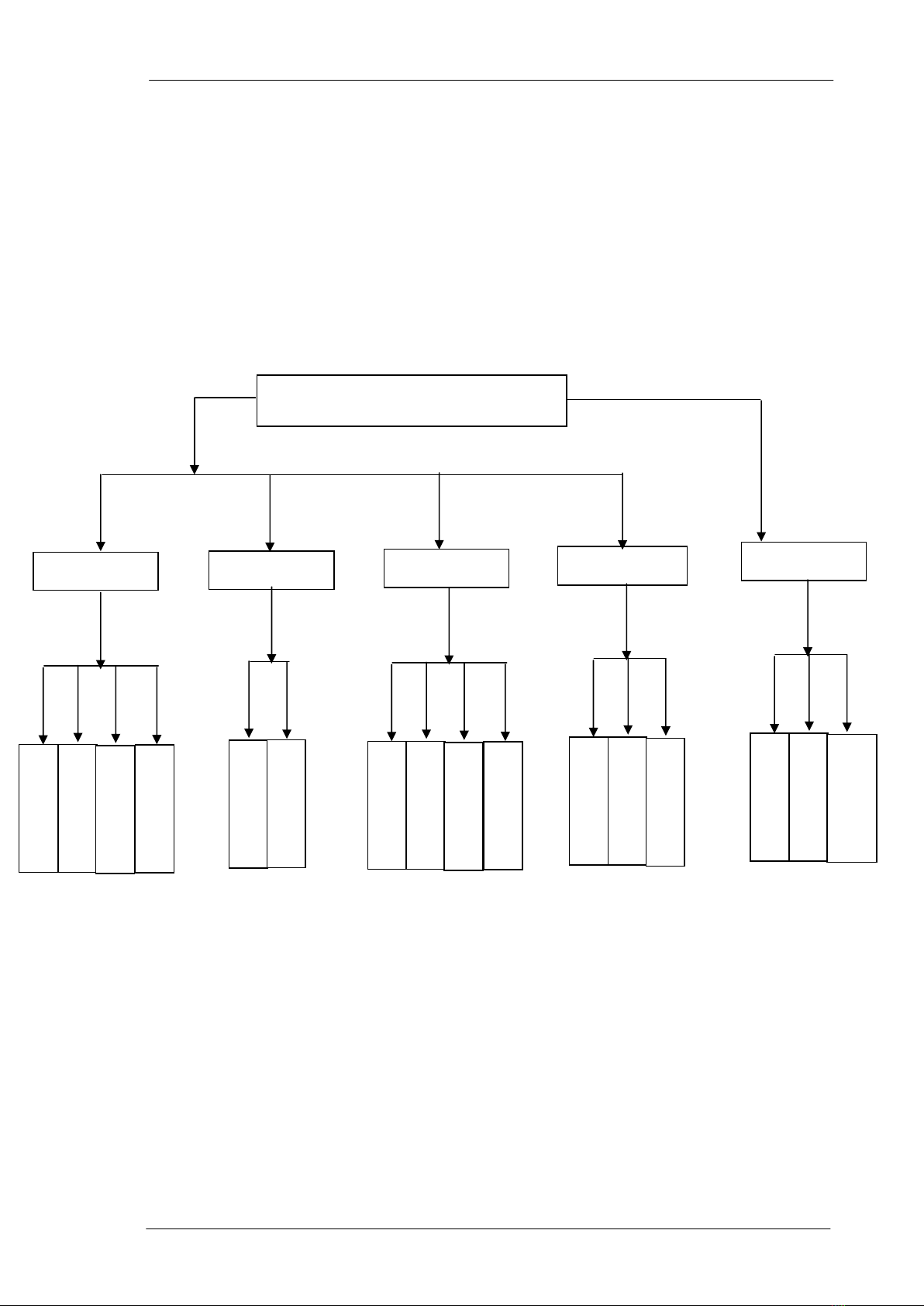
VIÖT NAM ®îc m« t¶ nh (H×nh1.1)

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

Lãi T§CT

Lãi ®Þa chÝnh

Lãi ®o vÏ

Lãi khu vùc

Lãi nhµ níc

T C

g n ¹ d n Õ i b

c ¨ i g a §

I g n ¹ H

i é h o a i G

I I g n ¹ H

I h c Ý t i ¶ i G

I g n ¹ H

I h n Ý h c a Þ §

I I I g n ¹ H

I I h c Ý t i ¶ i G

c ¾ r t n a u q i í L

I I h n Ý h c a Þ §

á h n c ¸ i g m a T

ë s ¬ c h n Ý h c a Þ §

T C g n « c i h t i í L

n Ò y u h c g n ê §

t ¸ s o ¶ h k i í L

Líi tr¾c ®Þa mÆt b»ng

Cao B¸ H¹

-4 -

Líp Tr¾c ®ÞaB-K48

H×nh 1.1 Ph©n lo¹i líi khèng chÕ tr¾c ®Þa mÆt b»ng

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

Tuy môc ®Ých thµnh lËp cã kh¸c nhau nhng nh×n chung, líi tr¾c ®Þa

c«ng tr×nh chñ yÕu vÉn ®îc lËp theo c¸c ph¬ng ph¸p truyÒn thèng ®· biÕt

nh: ph¬ng ph¸p tam gi¸c, ®a gi¸c hay giao héi. Ngoµi ra líi tr¾c ®Þa c«ng

tr×nh cßn ®îc thµnh lËp theo c¸c ph¬ng ph¸p ®Æc biÖt nh líi tø gi¸c kh«ng

®êng chÐo, líi « vu«ng x©y dùng, líi tam gi¸c nhá ®o oµn c¹nh ®é chÝnh

x¸c cao, líi nh÷ng tam gi¸c bÑt… HiÖn nay, c«ng nghÖ GPS ®· tõng bíc

®îc øng dông trong tr¾c ®Þa c«ng tr×nh ë níc ta nhng nh×n chung, viÖc lËp

líi tr¾c ®Þa c«ng tr×nh b»ng c¸c trÞ ®o mÆt ®Êt vÉn ®ang chiÕm vÞ trÝ chñ yÕu.

§é chÝnh x¸c cña líi tr¾c ®Þa c«ng tr×nh ®îc quy ®Þnh “ Tuú thuéc vµo

nh÷ng yªu cÇu vµ nhiÖm vô cô thÓ mµ nã ph¶i gi¶i quyÕt tuú theo tõng giai

®o¹n kh¶o s¸t thiÕt kÕ, thi c«ng x©y dùng vµ khai th¸c sö dông”.

VÞ trÝ mËt ®é vµ sè lîng c¸c ®iÓm khèng chÕ tuú thuéc môc ®Ých thµnh

lËp vµ ®Æc ®iÓm kü thuËt cña tõng lo¹i c«ng tr×nh.

Theo ®é chÝnh x¸c líi tr¾c ®Þa c«ng tr×nh ®îc ph©n thµnh hai trêng

hîp:

+ Trêng hîp 1: Líi tr¾c ®Þa c«ng tr×nh cã ®é chÝnh x¸c t¬ng ®¬ng líi ®o vÏ b¶n ®å (thêng gÆp trong thêi kú kh¶o s¸t c«ng tr×nh ®Ó ®o vÏ ®Þa h×nh c«ng tr×nh).

Trong trêng hîp nµy c¬ së ®Ó íc tÝnh sai sè trung ph¬ng cña bËc líi cÊp cuèi cïng (líi ®o vÏ) so víi líi khu vùc hoÆc nhµ níc kh«ng vît qu¸ ± 0, 2 mm.M. Líi tr¾c ®Þa c«ng tr×nh lóc nµy cã thÓ ph¸t triÓn dùa trªn c¸c ®iÓm cña líi nhµ níc theo nguyªn t¸c chung tõ tæng qu¸t ®Õn chi tiÕt.

+ Trêng hîp 2: Líi tr¾c ®Þa c«ng tr×nh cã yªu cÇu ®é chÝnh x¸c cao h¬n h¼n so víi líi ®o vÏ b¶n ®å (thêng gÆp trong giai ®o¹n thi c«ng, sö dông c«ng tr×nh). Trong trêng hîp nµy cÇn ph¶i lËp líi chuyªn dïng cho c«ng tr×nh.

Cao B¸ H¹

-5 -

Líp Tr¾c ®ÞaB-K48

Trong trêng hîp thø nhÊt líi tr¾c ®Þa c«ng tr×nh ®îc ph¸t triÓn theo nguyªn t¾c chung tõ tæng qu¸t ®Õn chi tiÕt vµ lÊy c¸c ®iÓm khèng chÕ nhµ níc lµm c¬ së (coi c¸c ®iÓm ®ã kh«ng cã sai sè). C¬ së íc tÝnh ®é chÝnh x¸c cho líi tr¾c ®Þa c«ng tr×nh lóc nµy lµ sai sè trung ph¬ng vÞ trÝ ®iÓm yÕu bËc líi cÊp cuèi cïng so víi c¸c ®iÓm cña líi bËc cao kh«ng qu¸ ± 0, 2 mm.M.

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

Trong trêng hîp thø hai c¸c ®iÓm cña líi nhµ níc nÕu cã trªn khu vùc chØ ®îc sö dông nh lµ sè liÖu ®Ó ®Þnh híng vµ ®Þnh vÞ cho líi tr¾c ®Þa c«ng tr×nh.

1.1.2. Líi khèng chÕ ®é cao

Líi khèng chÕ ®é cao ®îc lËp trªn khu vùc x©y dùng c«ng tr×nh lµ c¬ së tr¾c ®Þa phôc vô cho ®o vÏ ®Þa h×nh c«ng tr×nh, cho thi c«ng c«ng tr×nh vµ cho quan tr¾c chuyÓn dÞch biÕn d¹ng c«ng tr×nh.

Líi ®é cao tr¾c ®Þa c«ng tr×nh cè thÓ ®îc thµnh lËp theo c¸c d¹ng sau: Ph¬ng ph¸p thñy chuÈn h×nh häc tia ng¾m ng¾n, ph¬ng ph¸p ®o cao lîng gi¸c tia ng¾m ng¾n, ph¬ng ph¸p thñy chuÈn thñy tÜnh.

ChÝnh v× môc ®Ých hµnh lËp nh trªn nªn líi ®é cao tr¾c ®Þa c«ng tr×nh

còng cã nh÷ng ®Æc ®iÓm kh¸c so víi líi ®é cao nhµ níc:

Thø nhÊt: CÊp h¹ng líi khèng chÕ ®é cao ®îc quy ®Þnh tuú thuéc vµo diÖn tÝch khu vùc x©y dùng c«ng tr×nh:

B¶ng 1.1

DiÖn tÝch x©y dùng CÊp h¹ng thñy chuÈn

I, II, III, IV

II, III, IV

III, IV

> 500 km 2 50  500 km 2 10  50 km 2 < 10 km 2 IV

Thø hai: ®Ó phôc vô cho ®o vÏ ®Þa h×nh c«ng tr×nh th× líi ®é cao tr¾c ®Þa c«ng tr×nh ®îc ph¸t triÓn dùa trªn c¸c ®iÓm cña líi ®é cao nhµ níc theo nguyªn t¾c tõ tæng qu¸t ®Õn chi tiÕt.

Thø ba: ®Ó thi c«ng c«ng tr×nh, líi ®é cao cÇn ph¶i ®îc x©y dùng tuú thuéc vµo ®Æc ®iÓm vµ yªu cÇu kü thuËt cña tõng lo¹i c«ng tr×nh, vµ ®iÓm quan träng lµ ph¶i ®îc ®o nèi víi líi ®é cao nhµ níc.

Cao B¸ H¹

-6 -

Líp Tr¾c ®ÞaB-K48

Thø t: so víi líi nhµ níc th× mËt ®é c¸c ®iÓm líi tr¾c ®Þa c«ng tr×nh dµy h¬n, do ®ã chiÒu dµi ®îc rót ng¾n. §Ó thÊy râ ta t×m hiÓu mét sè chØ tiªu cña líi ®é cao tr¾c ®Þa c«ng tr×nh:

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

B¶ng 1.2

ChØ tiªu kü thuËt CÊp h¹ng thñy chuÈn

H¹ng II H¹ng III H¹ng IV

ChiÒu dµi lín nhÊt (km):

- Gi÷a c¸c ®iÓm gèc: 40/270 15/65 4/15

(c«ng tr×nh/nhµ níc)

- Gi÷a c¸c ®iÓm nót: 10/140 3/25 2/6

(c«ng tr×nh/nhµ níc)

Kho¶ng c¸ch gi÷a c¸c mèc thuû

chuÈn (km):

- Khu vùc x©y dùng: 2 0.2 0.2  0.5

- Khu vùc cha x©y dùng: 5 0.8 0.5  2.0

Sai sè khÐp giíi h¹n cña tuyÕn: 5 L 10 L 20 L

( L tÝnh km) (mm) (mm) (mm)

1.2. Nguyªn t¾c íc tÝnh líi tr¾c ®Þa c«ng tr×nh

Trªn c¬ së nh÷ng tµi liÖu thu thËp ®îc vµ yªu cÇu ®é chÝnh x¸c bè trÝ

c«ng tr×nh ta dù tÝnh ®é chÝnh x¸c cho líi vµ tiÕn hµnh íc tÝnh ®é chÝnh x¸c

líi. Cã hai ph¬ng ph¸p íc tÝnh ®é chÝnh x¸c c¸c yÕu tè cña m¹ng líi lµ

ph¬ng ph¸p íc tÝnh chÆt chÏ vµ ph¬ng ph¸p gÇn ®óng.

1.2.1. Ph¬ng ph¸p íc tÝnh gÇn ®óng

Tríc kia, khi c¸c ph¬ng tiÖn phôc vô c«ng t¸c ®o ®¹c vµ tÝnh to¸n líi

cha nhiÒu th× ngêi ta thêng thiÕt kÕ líi theo mét sè d¹ng ®å h×nh mÉu nh

chuçi tam gi¸c, líi ®a gi¸c trung t©m, líi ®êng chuyÒn… vµ sö dông c¸c

c«ng thøc lËp s½n trªn c¬ së bµi to¸n b×nh sai ®iÒu kiÖn vµ chØ tËp trung xem

xÐt mét sè yÕu tè ®Æc trng ë vÞ trÝ yÕu nhÊt cña m¹ng líi. VÝ dô nh khi íc

tÝnh ®é chÝnh x¸c cña chuçi tam gi¸c, ®a gi¸c trung t©m, … ngêi ta thiÕt kÕ

líi theo d¹ng ®å h×nh mÉu ®¬n gi¶n vµ sñ dông c¸c c«ng thøc ®îc lËp s½n

Cao B¸ H¹

-7 -

Líp Tr¾c ®ÞaB-K48

theo d¹ng nh÷ng ®å h×nh ®ã. Sau ®©y lµ mét sè vÝ dô.

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

1.2.1.1. íc tÝnh ®é chÝnh x¸c chuçi tam gi¸c

H×nh 1.2 §å h×nh chuçi tam gi¸c

Víi chuçi tam gi¸c cã d¹ng nh H×nh 2.1 th× ®é chÝnh x¸c c¸c yÕu tè ë vÞ

trÝ yÕu nhÊt ®îc ®Æc trng bëi c¸c sai sè:

Sai sè trung ph¬ng chiÒu dµi c¹nh yÕu:

Ký hiÖu: m lµ sai sè trung ph¬ng chiÒu dµi c¹nh EF tÝnh theo ®êng (1)

lµ sai sè trung ph¬ng chiÒu dµi c¹nh EF tÝnh theo ®êng (2) m

2 s

Lóc ®ã träng sè chiÒu dµi c¹nh EF ®îc tÝnh theo nguyªn t¾c céng träng sè.

m 2 s

 1sm

 2sm

2 m  s 1 2 mm . s 1

+ = 2 . P EF = P 1+ P 2 =

mm . s

Sai sè trung ph¬ng chiÒu dµi c¹nh EF:

EFS =



 EFP

2 s

2 s 1

m .

)



( 









m = ± (1.1)

2 A

2 B

2 C

2 

2 . m . 

lg 1sm =

2 3

1S , m

2S ®îc x¸c ®Þnh th«ng qua sai sè trung ph¬ng loga chiÒu dµi c¹nh:



Sm . s lg 6 10.



(1.2)

μ = m  víi m  lµ sai sè trung ph¬ng ®o gãc dù kiÕn.

Sai sè trung ph¬ng ph¬ng vÞ c¹nh yÕu: nÕu ®o hai ®Çu th× ph¬ng vÞ

 mm , 

yÕu nhÊt lµ ph¬ng vÞ c¹nh ë gi÷a. T¬ng tù nh trªn, gäi lµ sai sè

trung ph¬ng ph¬ng vÞ c¹nh EF tÝnh theo ®êng (1) vµ (2) th× ta còng sÏ tÝnh

m

Cao B¸ H¹

-8 -

Líp Tr¾c ®ÞaB-K48

®îc sai sè trung ph¬ng ph¬ng vÞ c¹nh yÕu lµ:

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

mm .  

m = ±



2 m 

(1.3)

(

2 s .)





Sai sè trung ph¬ng t¬ng hç vÞ trÝ ®iÓm:

2 s

m  

(1.4)

1.2.1.1. íc tÝnh ®é chÝnh x¸c ®a gi¸c trung t©m D

H×nh 1.3 §å h×nh ®a gi¸c trung t©m

§èi víi ®a gi¸c trung t©m nh h×nh 1.3, viÖc íc tÝnh ®é chÝnh x¸c cã thÓ

thùc hiÖn theo nh íc tÝnh ®é chÝnh x¸c cña chuçi tam gi¸c ®¬n nhng trong



b 1

b 2

b 0



m 

0

trêng hîp nµy chØ xuÊt ph¸t tõ mét c¹nh ®¸y AB = b 0 , tøc:





Do ®ã ®èi víi c¹nh DE = S, ta cã:

2 lg

b 0

S 10.

2 lg m



2 mm lg s 1 2 lg

2 lg

s 1





(1.5)

m 

2 m 



2 2 mm .   2 2 2 m m  

Cao B¸ H¹

-9 -

Líp Tr¾c ®ÞaB-K48

Vµ (1.6)

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

m ®îc tÝnh trong

ibmlg

Trong c¸c c«ng thøc trªn, c¸c ®¹i lîng vµ

trêng hîp kh«ng kÓ ®Õn ¶nh hëng cña sai sè sè liÖu gèc.

NhËn xÐt: ph¬ng ph¸p íc tÝnh gÇn ®óng cã u ®iÓm lµ néi dung tÝnh to¸n

®¬n gi¶n nhng nhîc ®iÓm lµ chØ xem xÐt ®îc c¸c yÕu tè yÕu nhÊt trong

m¹ng líi, tõ ®ã kÕt luËn cho ®é chÝnh x¸c cña toµn m¹ng líi, do ®ã kh«ng

kh¸ch quan vµ khi ¸p dông ra ngoµi thùc tÕ th× ®é sai lÖch lín.

1.2.2. íc tÝnh chÆt chÏ ®é chÝnh x¸c líi thiÕt kÕ

Khi x©y dùng mét m¹ng líi tr¾c ®Þa, th«ng thêng chóng ta ph¶i ph©n

tÝch, íc tÝnh ®é chÝnh x¸c cña m¹ng líi thiÕt kÕ nh»m ®¸nh gi¸ chÊt lîng

m¹ng líi thiÕt kÕ cã ®¶m b¶o c¸c yªu cÇu vÒ ®é chÝnh x¸c hay kh«ng, trªn c¬

së ®ã cã sù ®iÒu chØnh ®å h×nh, lùa chän m¸y mãc vµ trang thiÕt bÞ ®Ó cã

ph¬ng ¸n ®o hîp lý, ®¶m b¶o ®é chÝnh x¸c cña ®å h×nh thiÕt kÕ ®· lùa chän.

§é chÝnh x¸c cña m¹ng líi tr¾c ®Þa ®îc quyÕt ®Þnh bëi ®é chÝnh x¸c ®o

®¹c vµ kÕt cÊu ®å h×nh cña líi. Sai sè trung ph¬ng cña mét yÕu tè bÊt kú



trong líi ®îc x¸c ®Þnh theo c«ng thøc:

m F

1 P F

(1.7)

Trong ®ã:  lµ Sai sè trung ph¬ng träng sè ®¬n vÞ ®Æc trng cho ®é chÝnh

x¸c ®o ®¹c dù kiÕn.

1/PF lµ träng sè ®¶o cña c¸c yÕu tè cÇn ®¸nh gi¸ ®é chÝnh x¸c, gi¸

trÞ nµy phô thuéc vµo kÕt cÊu ®å h×nh.

mF lµ Sai sè trung ph¬ng cña hµm yÕu tè cÇn ®¸nh gi¸, (vÝ dô:

chiÒu dµi, ph¬ng vÞ, to¹ ®é, ®é cao ...).

C«ng thøc (1.7) biÓu thÞ cho mèi t¬ng quan gi÷a ba ®¹i lîng mF, ,

1/PF. NÕu cho biÕt hai trong ba ®¹i lîng nªu trªn th× chóng ta cã thÓ x¸c ®Þnh ®îc ®¹i lîng cßn l¹i. Tõ ®ã cã c¸c bµi to¸n íc tÝnh ®é chÝnh x¸c sau:

* Bµi to¸n 1: Cho biÕt sai sè ®o ®¹c dù kiÕn () vµ ®å h×nh líi (1/PF). TÝnh ®é

Cao B¸ H¹

-10 -

Líp Tr¾c ®ÞaB-K48

chÝnh x¸c c¸c yÕu tè trong líi (mF).

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

* Bµi to¸n 2: Cho biÕt sai sè ®o ®¹c dù kiÕn () vµ yªu cÇu ®é chÝnh x¸c trong

líi (mF). X¸c ®Þnh ®å h×nh líi (1/PF).

* Bµi to¸n 3: Cho biÕt ®å h×nh líi (1/PF) vµ yªu cÇu ®é chÝnh x¸c trong líi

(mF). X¸c ®Þnh sai sè ®o ®¹c cÇn thiÕt ().

Trong tr¾c ®Þa, c«ng viÖc íc tÝnh ®é chÝnh x¸c cña c¸c yÕu tè ®Æc trng

trong líi ®îc sö dông theo hai ph¬ng ph¸p:

- Ph¬ng ph¸p íc tÝnh gÇn ®óng

- Ph¬ng ph¸p íc tÝnh chÆt chÏ.

§èi víi ph¬ng ph¸p íc tÝnh gÇn ®óng chØ ¸p dông cho nh÷ng ®å h×nh

®¬n gi¶n, Ýt trÞ ®o, cßn ®èi víi nh÷ng ®å h×nh phøc t¹p, cã yªu cÇu ®é chÝnh

x¸c cao th× ta sö dông ph¬ng ph¸p íc tÝnh chÆt chÏ.

Ph¬ng ph¸p íc tÝnh chÆt chÏ dùa trªn c¬ së cña ph¬ng ph¸p b×nh sai

gi¸n tiÕp hoÆc b×nh sai ®iÒu kiÖn. HiÖn nay, víi sù ph¸t triÓn cña c«ng nghÖ tin

häc cã thÓ thµnh lËp ch¬ng tr×nh íc tÝnh theo ph¬ng ph¸p b×nh sai gi¸n tiÕp

víi quy tr×nh nh sau:

1. Chän Èn sè: lµ täa ®é (®é cao) c¸c ®iÓm cÇn x¸c ®Þnh trong líi.





2. LËp hÖ ph¬ng tr×nh sè hiÖu chØnh

(1.8)

trong ®ã :

A – Ma trËn hÖ sè

X – Vector Èn sè

V, L – Vector hiÖu chØnh vµ vector sè h¹ng tù do

0 b

3. LËp hÖ ph¬ng tr×nh chuÈn

T PAAR



(1.9)



  T PLAb 

Cao B¸ H¹

-11 -

Líp Tr¾c ®ÞaB-K48

Víi (1.10)

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

1 RQ

4. NghÞch ®¶o ma trËn hÖ sè hÖ ph¬ng tr×nh chuÈn:

(1.11)

5. LËp hµm träng sè

(1.12) - Träng sè c¹nh FS = Si

T QFs

1 sFp

= Fs

- Träng sè ph¬ng vÞ

(1.13) Fα = i

T QF

1 Fp

= F

6. §¸nh gi¸ ®é chÝnh x¸c

- Sai sè trung ph¬ng cña c¸c Èn sè:

iiQ

(1.14) Mxi = 

- Sai sè trung ph¬ng cña hµm c¸c Èn sè:

1 FP

(1.15) MF =

Sau khi ®· íc tÝnh xong, ®èi chiÕu víi yªu cÇu ®é chÝnh x¸c xem kÕt qu¶ íc

tÝnh líi cã ®¹t kh«ng.

- NÕu líi kh«ng ®¹t ®é chÝnh x¸c th× tiÕn hµnh hiÖu chØnh líi, nÕu hiÖu

chØnh mµ vÉn kh«ng ®¹t th× ph¶i thiÕt kÕ vµ íc tÝnh l¹i líi.

- NÕu kÕt qu¶ íc tÝnh ®¹t chóng ta tiÕn hµnh lùa chän thiÕt bÞ m¸y mãc

vµ ph¬ng ¸n ®o ®¹c.

NhËn xÐt: viÖc íc tÝnh ®é chÝnh x¸c cña líi theo ph¬ng ph¸p chÆt chÏ cho

phÐp chóng ta cã thÓ ®¸nh gi¸ ®é chÝnh x¸c cña bÊt kú yÕu tè nµo trong m¹ng

Cao B¸ H¹

-12 -

Líp Tr¾c ®ÞaB-K48

líi thiÕt kÕ víi ®é chÝnh x¸c cao. HiÖn nay, øng dông tin häc vµo tr¾c ®Þa ®·

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

rÊt phæ biÕn nªn c¸c ch¬ng tr×nh ®¸nh gi¸ ®é chÝnh x¸c c¸c yÕu tè cña líi

cho ta kÕt qu¶ nhanh vµ chÝnh x¸c, gi¶m ®îc khèi lîng tÝnh to¸n lín.

1.3. Lùa chän hÖ to¹ ®é vµ mÆt chiÕu cho líi tr¾c ®Þa

c«ng tr×nh

Líi khèng chÕ tr¾c ®Þa c«ng tr×nh ®îc thµnh lËp bëi c¸c trÞ ®o cã thÓ lµ

gãc, c¹nh hoÆc ph¬ng vÞ. V× c¸c c«ng tr×nh ®îc x©y dùng trªn bÒ mÆt tù

nhiªn cña tr¸i ®Êt nªn c¸c c«ng t¸c tr¾c ®Þa còng ®îc tiÕn hµnh trªn bÒ mÆt

nµy. Song bÒ mÆt tù nhiªn rÊt phøc t¹p nªn ta kh«ng thÓ dïng lµm mÆt chuÈn

®Ó tÝnh to¸n b×nh sai c¸c trÞ ®o. VÒ nguyªn t¾c, khi b×nh sai líi tr¾c ®Þa mÆt

b»ng cÇn chän ra mét bÒ mÆt to¸n häc ®Ó biÓu diÔn c¸c trÞ ®o vµ tÝnh to¸n b×nh

sai tr¾c ®Þa. MÆt ®îc chän lµ mÆt Elipxoid thùc dông, ®îc ®Þnh vÞ phï hîp

víi l·nh thæ cña tõng quèc gia. V× vËy, tríc khi b×nh sai líi tr¾c ®Þa mÆt

b»ng, cÇn ph¶i chiÕu c¸c trÞ ®o tõ mÆt ®Êt vÒ mÆt Elipxoid thùc dông.

Môc ®Ých cuèi cïng cña c«ng t¸c x©y dùng m¹ng líi tr¾c ®Þa lµ x¸c ®Þnh

vÞ trÝ cña c¸c ®iÓm trªn mÆt Elipxoid quy chiÕu ®îc chän. §Ó x¸c ®Þnh vÞ trÝ

c¸c ®iÓm trong thùc tÕ thêng sö dông hai hÖ to¹ ®é lµ hÖ täa ®é tr¾c ®Þa vµ hÖ

to¹ ®é vu«ng gãc ph¼ng. Tuy nhiªn, hÖ to¹ ®é tr¾c ®Þa kh«ng ®îc sö dông

réng r·i trong tr¾c ®Þa c«ng tr×nh lµ do vÞ trÝ c¸c ®iÓm trªn mÆt Elipxoid ®îc

x¸c ®Þnh b»ng c¸c ®¬n vÞ gãc, chiÒu dµi cung trªn mÆt elipxoid t¬ng øng, c¸c

®¬n vÞ nµy l¹i thay ®æi theo vÜ ®é, vµ c¸c kinh tuyÕn dïng ®Ó x¸c ®Þnh c¸c gãc

ph¬ng vÞ tr¾c ®Þa l¹i kh«ng song song víi nhau nªn khi sö dông c¸c sè liÖu

®ã ta l¹i ph¶i xÐt thªm tÝnh kh«ng song song ®ã. Ngoµi ra, c¸c c«ng thøc ®Ó

gi¶i bµi to¸n tr¾c ®Þa dï ë kho¶ng c¸ch ng¾n còng rÊt phøc t¹p. Trªn thùc tÕ,

®Ó thuËn tiÖn ngêi ta thêng sö dông hÖ to¹ ®é vu«ng gãc ph¼ng, viÖc tÝnh

to¸n trªn hÖ to¹ ®é nµy ®îc tiÕn hµnh nhanh chãng dÔ dµng víi c¸c c«ng thøc

h×nh häc vµ lîng gi¸c ph¼ng. To¹ ®é ph¼ng c¸c ®iÓm cña líi ®îc tÝnh trong

mÆt ph¼ng cña phÐp chiÕu Gauss-Kruger hoÆc UTM. Thùc chÊt cña phÐp

chiÕu lµ ®a vµo c¸c trÞ ®o c¸c sè hiÖu chØnh t¬ng øng do ®é xa kinh tuyÕn vµ

Cao B¸ H¹

-13 -

Líp Tr¾c ®ÞaB-K48

do ®é cao mÆt chiÕu g©y ra.

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

C«ng tr×nh ®îc x©y dùng trªn mÆt ®Êt, do vËy ®Ó b¶o ®¶m cho thiÕt kÕ

vµ thi c«ng c«ng tr×nh th× líi tr¾c ®Þa c«ng tr×nh cÇn ph¶i ®îc tÝnh to¸n sao

cho kh«ng ph¶i c¶i chÝnh c¸c sè hiÖu chØnh do c¸c phÐp chiÕu g©y ra, nãi c¸ch

kh¸c lµ ph¶i chän hÖ to¹ ®é vµ mÆt chiªu sao cho c¸c sè hiÖu chØnh nµy xÊp xØ

b»ng 0.

1.3.1. Chän ®é cao mÆt chiÕu cho líi tr¾c ®Þa c«ng tr×nh

Sè hiÖu chØnh do ®é cao mÆt chiÕu ®îc x¸c ®Þnh theo c«ng thøc sau:

H 0 M R

S (1.16) ΔS H = -

MH : §é cao trung b×nh cña c¹nh AB

0H : §é cao mÆt chiÕu

MR : B¸n KÝnh trung b×nh cña Elipx«id

Trong ®ã:

B’

A’ ’A

S: ChiÒu dµi AB ®o ®îc (®· ®a vÒ n»m ngang)

H×nh 1.4. MÆt chiÕu líi tr¾c ®Þa c«ng tr×nh

§Æt ®iÒu kiÖn: ΔS H = 0

0H = MH

Cao B¸ H¹

-14 -

Líp Tr¾c ®ÞaB-K48

Tõ (1.16) gi¶i ra ta ®îc: (1.17)

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

Tõ (1.17) cã thÓ thÊy: §é cao mÆt chiÕu cña líi tr¾c ®Þa c«ng tr×nh ®îc

chän lµ ®é cao trung b×nh cña khu vùc x©y dùng c«ng tr×nh.

1.3.2. Chän hÖ to¹ ®é cho líi tr¾c ®Þa c«ng tr×nh

Sè hiÖu chØnh do ®é xa kinh tuyÕn ®îc viÕt nh sau:

Y 2 R

(1.18) )S ΔS F = ( k 0 - 1 +

MY lµ tung ®é trung b×nh cña c¹nh ®o (®Æc trng cho ®é xa kinh tuyÕn

Trong ®ã: k 0 lµ hÖ sè cña mói chiÕu.

trung ¬ng).

2).

§Ó chän hÖ täa ®é cho líi tr¾c ®Þa c«ng tr×nh ta ®Æt ®iÒu kiÖn: ΔS F = 0

0k

(1.19) Tõ (1.18) gi¶i ra ta ®îc: MY = MR

MY = 90 km (víi mói 6 0 ,

Khi sö dông phÐp chiÕu UTM th× ta cã

MY = 180 km (víi mói 3 0 , k 0 =0.9999). Khi sö dông phÐp

k 0 =0.9996) vµ

chiÕu Gauss – Kruger th× MY = 0 km.

§iÒu ®ã cã nghÜa lµ ®iÓm gèc to¹ ®é cña hÖ to¹ ®é c«ng tr×nh ®îc chän c¸ch

xa khu vùc x©y dùng mét kho¶ng c¸ch ®óng b»ng MY .

1.4. TÝnh chuyÓn to¹ ®é

Trªn khu vùc x©y dùng c«ng tr×nh thêng gÆp c¸c hÖ to¹ ®é: hÖ to¹ ®é

nhµ níc, hÖ to¹ ®é gi¶ ®Þnh vµ hÖ to¹ ®é c«ng tr×nh.

HÖ to¹ ®é nhµ níc: Trªn khu vùc x©y dùng c«ng tr×nh thêng cã s½n

nh÷ng ®iÓm cña líi nhµ níc phôc vô cho c«ng t¸c ®o vÏ ®Þa h×nh hoÆc ®o vÏ

®Þa chÝnh, c¸c ®iÓm nµy ®Òu ®îc x©y dùng trong hÖ to¹ ®é nhµ níc. HiÖn

nay ®Ó thuËn tiÖn cho viÖc sö dông hÖ to¹ ®é chung trong khu vùc vµ thÕ giíi,

níc ta sö dông hÖ to¹ ®é VN- 2000 thay thÕ cho hÖ to¹ ®é HN- 72 tríc kia.

HÖ to¹ ®é sö dông phÐp chiÕu UTM nµy ®îc x©y dung nh sau:

Cao B¸ H¹

-15 -

Líp Tr¾c ®ÞaB-K48

- Elipxoid quy chiÕu lµ elipxoid WGS- 84 víi c¸c th«ng sè:

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

B¶ng 1.3

B¸n trôc lín a= 6378137.0 m

§é dÑt f= 1/298.257223563

Tèc ®é gãc quay quanh trôc w= 7291115.10 11 rad/s

H»ng sè träng trêng tr¸i ®Êt G M = 3986005.10 8 m 3 /s 2

- Chän ®é cao mÆt chiÕu lµ bÒ mÆt níc biÓn trung b×nh t¹i ®¶o Hßn

DÊu, H¶i Phßng.

- §iÓm gèc to¹ ®é N00 ®îc ®Æt t¹i viÖn nghiªn cøu ®Þa chÝnh, ®êng

Hoµng Quèc ViÖt, Hµ Néi.

HÖ to¹ ®é quy íc: Lµ hÖ to¹ ®é ®îc lùa chän theo quy íc cña ngêi

sö dông. Th«ng thêng trong x©y dung c¸c c«ng tr×nh, ngêi ta thêng chän

gèc to¹ ®é lµ mét trong nh÷ng ®iÓm cña líi thuéc trôc chÝnh, trôc x trïng víi

trôc chÝnh c«ng tr×nh.

HÖ to¹ ®é c«ng tr×nh: Lµ hÖ to¹ ®é mµ mÆt chiÕu vµ gèc to¹ ®é ®îc lùa

chän phï hîp víi ®Æc ®iÓm cña tõng lo¹i c«ng tr×nh. Tõ viÖc nghiªn cøu ¶nh

hëng cña c¸c sè liÖu chØnh do ®é cao mÆt chiÕu vµ ®é xa kinh tuyÕn trong

phÇn trªn, ngêi ta lùa chän hÖ to¹ ®é nay nh sau:

- Gèc cña hÖ to¹ ®é ®îc chän c¸ch xa khu vùc x©y dung c«ng tr×nh trªn

mói chiÕu 3 0 vµ mói chiÕu 6 0 lÇn lît lµ 90 km vµ 180 km (±10 km) khi sö

dông phÐp chiÕu UTM.

- §é cao mÆt chiÕu ®îc chän lµ ®é cao trung b×nh cña khu vùc x©y

dùng.

Líi khèng chÕ thi c«ng ®ãng vai trß rÊt quan träng trong qu¸ tr×nh x©y

dùng c«ng tr×nh, chÊt lîng líi khèng chÕ thi c«ng sÏ ®¶m b¶o tÝnh chÝnh

x¸c cña c«ng tr×nh trong thêi gian x©y dung còng nh khi vËn hµnh ®a c«ng

Cao B¸ H¹

-16 -

Líp Tr¾c ®ÞaB-K48

tr×nh vµo sö dông. Mét trong nh÷ng yªu cÇu c¬ b¶n khi thµnh lËp líi khèng

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

chÕ thi c«ng lµ cÇn cã sù ®ång nhÊt vÒ hÖ quy chiÕu gi÷a líi khèng chÕ thi

c«ng cÇn thµnh lËp víi hÖ to¹ ®é ®· ®îc sö dông ®Ó thiÕt kÕ c«ng tr×nh.

§Ó thèng nhÊt c¸c hÖ thèng to¹ ®é trªn khu vùc x©y dung c«ng tr×nh,

chóng ta sö dông bµi to¸n tÝnh chuyÓn to¹ ®é. §Ó phôc vô cho c«ng t¸c tÝnh

chuyÓn to¹ ®é chóng ta cã thÓ sö dông nhiÒu c«ng thøc kh¸c nhau tuú thuéc

vµo yªu cÇu chuyÓn ®æi to¹ ®é trong mét hÖ quy chiÕu hay gi÷a c¸c hÖ quy

chiÕu víi nhau.

1.4.1. Bµi to¸n tÝnh chuyÓn to¹ ®é gi÷a c¸c mói chiÕu trong cïng elipxoid

Trong mét hÖ quy chiÕu bao gåm hÖ to¹ ®é vu«ng gãc kh«ng gian ®Þa

t©m cã t©m trïng víi elipxoid tr¸i ®Êt cã kÝch thíc x¸c ®Þnh. Trªn elipxoid

nµy ngêi ta x¸c lËp hÖ to¹ ®é tr¾c ®Þa B, L, H. BÒ mÆt elipxoid nµy l¹i ®îc

chia thµnh nhiÒu mói vµ mçi mói ®îc chiÕu lªn mÆt ph¼ng theo ph¸p chiÕu

Gauss- Kruger hoÆc UTM.

Gi¶ sö cã mét ®iÓm cã to¹ ®é x 1, y 1 ë mói chiÕu cã kinh tuyÕn trung

¬ng L 1, ta cÇn tÝnh chuyÓn vÒ to¹ ®é x 2 , y 2 ë mói chiÕu cã kinh tuyÕn trung

¬ng lµ L 2 , ta lµm nh sau:

- Tõ to¹ ®é x1y1 ë mói chiÕu cã kinh tuyÕn trung ¬ng L1 tÝnh ®îc to¹ ®é

tr¾c ®Þa B,L

- Tõ to¹ ®é tr¾c ®Þa B,L tÝnh ®îc to¹ ®é vu«ng gãc ph¼ng x2y2 trªn mói

chiÕu cã kinh tuyÕn trung ¬ng lµ L2

Nh vËy to¹ ®é tr¾c ®Þa ®îc dïng lµm vai trß trung gian trong tÝnh to¸n.

C¸c c«ng thøc chuyÓn ®æi ®îc viÕt nh sau:

1.4.1.1. TÝnh ®æi tõ hÖ to¹ ®é vu«ng gãc ph¼ng x, y vÒ hÖ to¹ ®é tr¾c ®Þa B, L

To¹ ®é ph¼ng ®îc chuyÓn vÒ to¹ ®é tr¾c ®Þa cña ®iÓm t¬ng øng trªn

mÆt elipxoid theo c«ng thøc tæng qu¸t :

Cao B¸ H¹

-17 -

Líp Tr¾c ®ÞaB-K48

(1.20) B= F1(x,y) L= F2(x,y)

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

Khai triÓn c«ng thøc trªn thµnh chuçi hµm sè theo y ta ®îc c¸c c«ng



thøc tÝnh ®é vÜ vµ hiÖu ®é kinh tr¾c ®Þa nh sau:

0 )+12t 2

0 }-

0 +9ψ0(1-t 2

t 0 Mm 0

y 2 Nm 0

t 0 Mm 0

y 3 24 Nm 0

3 0

  

  

  

  

{-4ψ 2 B=B0–

0 (11- 24 t 2

0 )- 12ψ 3

0 (21- 71 t 2

0 )+ 15 ψ 2

0 (15- 98 t 2

0 + 15

y 720 Nm

t 0 Mm 0

5 0

   

   

{8ψ 4

0 -3 t 4

0 )+360 t 4

0 }+

0 +4095 t 4

0 +

0 )+180 ψ0(5 t 2 t 4

y 40320 Nm

t 0 Mm 0

7 0

  

  

(1385+ 3633 t 2

0 ) 1575 t 6

(1.21)

0 (1- 6t 2

0 )+

0 )+ secB0

y 120 Nm

y 0 Nm

5 0

y 3 6 Nm 0

3 0

  

  

   

   

   

   

{- 4ψ 3 l= secB0 - secB0 (ψ0+ 2 t 2

0 (9- 68t 2

0 + 24t 4

0 + 1320 t 4

0 +

0 )+ 72 ψ0t 2

0 }- secB0

y 5040 Nm

7 0

  

  

(61+ 662t 2 ψ 2

0 ) 720t 6

(1.22)

trong ®ã B0 lµ ®é vÜ gÇn ®óng øng víi chiÒu dµi cung kinh tuyÕn lµ x/m0

t0= tgB0

2 Ne ) 2 sin

0 B

1(  2 e 

a 2 sin



N0= ; M0=

N M

e 1

sin 2 e 

= ψ0=

1.4.1.2. TÝnh ®æi tõ hÖ to¹ ®é tr¾c ®Þa B, L vÒ hÖ to¹ ®é vu«ng gãc ph¼ng x, y

To¹ ®é ®iÓm trªn mÆt elipxoid ®îc chuyÓn vÒ to¹ ®é ph¼ng theo c«ng

thøc tæng qu¸t sau:

x= F1( B, L)

(1.23) y= F2( B, L)

HÖ to¹ ®é vu«ng gãc ph¼ng ®îc thiÕt lËp theo ph¸p chiÕu h×nh trô

ngang, theo mói chiÕu cã kinh tuyÕn trung ¬ng L 0 .

Sau ®©y lµ c«ng thøc tæng qu¸t cña phÐp chiÕu h×nh trô ngang ®ång gãc,

Cao B¸ H¹

-18 -

Líp Tr¾c ®ÞaB-K48

víi tû lÖ chiÕu trªn kinh tuyÕn trôc lµ m 0 :

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

2l 2

4l 24

cosB+ NsinB cos 3 B(4 2 +  - t 2 )+ x= m 0 [ X 0 + NsinB

2 (1- 32t 2 )-  (2t 2 )+ c}+

6l 720

NsinB cos 5 B{8 4 (11- 24t 2 )- 28 3 (1- 6t 2 )+

8l 40320

NsinB cos 7 B(1385- 3111t 2 + 543t 4 - t 6 )] (1.24)

2 (1+

5l 120

3l 6

cos 3 B( - t 2 )+ N cos 5 B{4 3 (1- 6t 2 )+ y= m 0 [ N l cosB+ N

7l 5040

8t 2 )- 2 t 2 + t 4 }+ N cos 7 B(61- 479t 2 + 179t 2 - t 6 )] (1.25)

Trong ®ã: X 0 lµ chiÒu dµi cung kinh tuyÕn tõ xÝch ®¹o ®Õn ®é vÜ B

HiÖu ®é kinh l = L- L 0 , víi L 0 lµ ®é kinh cña kinh tuyÕn trung ¬ng

t= tgB

 e

2 ) Ne 2 2 sin

0 B

1( 1 

a 2 sin

1 

)

 =

N= ; M=

N M

e  1(

)

sin 2 e 

Trong tr¾c ®Þa c«ng tr×nh, bµi to¸n tÝnh chuyÓn to¹ ®é gi÷a c¸c mói chiÕu

trong cïng mét elipxoid ®îc sö dông ®Ó tÝnh chuyÓn to¹ ®é tõ hÖ to¹ ®é nhµ

níc sang hÖ to¹ ®é c«ng tr×nh vµ ngîc l¹i.

1.4.1.3. TÝnh chuyÓn gi÷a c¸c hÖ to¹ ®é vu«ng gãc ph¼ng

§èi víi hai hÖ to¹ ®é vu«ng gãc ph¼ng liªn hÖ víi hai hÖ quy chiÕu kh¸c

nhau, trªn ph¹m vi kh«ng qu¸ lín chóng ta cã thÓ chuyÓn ®æi to¹ ®é theo c«ng

thøc 4 tham sè cña Helmert.

Nh ®· biÕt, c«ng thøc c¬ b¶n trong bµi to¸n chuyÓn ®æi to¹ ®é vu«ng

gãc ph¼ng lµ:

X i = X 0 + mx i cos - my i sin (1.26) Y i = Y 0 + my i cos + mx i sin

Cao B¸ H¹

-19 -

Líp Tr¾c ®ÞaB-K48

Trong ®ã: X i , Y i lµ to¹ ®é cña ®iÓm trong hÖ to¹ ®é thø hai

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

x i , y i lµ to¹ ®é cña ®iÓm trong hÖ to¹ ®é thø nhÊt

X 0 , Y 0 lµ c¸c gi¸ trÞ dÞch chuyÓn gèc to¹ ®é, chÝnh lµ to¹ ®é gèc

cña hÖ thø nhÊt trong hÖ thø hai (H×nh 1.5 )



x yi Yi

X0 i xi O’ Xi

Y0 y

Y O

 lµ gãc xoay hÖ trôc

H×nh 1.5. Bµi to¸n chuyÓn ®æi to¹ ®é Helmet

m lµ hÖ sè tû lÖ dµi cña hai hÖ

Trong trêng hîp nµy chóng ta thêng kh«ng tÝnh chuyÓn trùc tiÕp tõ hÖ

x, y sang hÖ X, Y mµ thêng tÝnh chuyÓn th«ng qua hÖ to¹ ®é träng t©m x’, y’

cã c¸c thµnh phÇn to¹ ®é ®îc x¸c ®Þnh nh sau:

x’ i = x i - x 0

(1.27) y’ i = y i - y 0

Trong ®ã x 0 , y 0 lµ träng t©m, ®îc tÝnh theo c«ng thøc:

  x n

  y n

(1.28) x 0 = ; y 0 =

Trong ®ã n lµ sè lîng ®iÓm tham gia tÝnh.

Nh vËy c¸c biÓu thøc (1.26) sÏ cã d¹ng:

X i = X 0 + mx’ i cos - my’ i sin

Cao B¸ H¹

-20 -

Líp Tr¾c ®ÞaB-K48

(1.29) Y i = Y 0 + my’ i cos + mx’ i sin

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

§Ó chuyÓn ®æi to¹ ®é tõ hÖ thø nhÊt sang hÖ thø hai, chóng ta cÇn x¸c

®Þnh 4 tham sè chuyÓn ®æi, ®ã lµ ®é lÖch gèc X 0 , Y 0 , gãc xoay  vµ tû lÖ dµi

m. Muèn x¸c ®Þnh ®îc 4 tham sè th× cÇn Ýt nhÊt 2 ®iÓm cã to¹ ®é trong c¶ hai

hÖ (gäi lµ ®iÓm song trïng).

Gi¶ sö chóng ta cã n ®iÓm song trïng , khi ®ã ta sÏ lËp ®îc 2n ph¬ng

tr×nh sè hiÖu chØnh d¹ng:

iX = X 0 + mx’ i cos - my’ i sin - X i

iY = Y 0 + my’ i cos + mx’ i sin - Y i

(1.30) V

NÕu coi c¸c ®iÓm ®o nèi cã ®é chÝnh x¸c nh nhau, ta sÏ gi¶i hÖ ph¬ng tr×nh

X + V 2

Y ]= min.

(1.30) theo ®iÒu kiÖn [V 2

Trong c¸c ph¬ng tr×nh (1.30) ta ký hiÖu:

m.cos = P

(1.31) m.sin = Q

2 Q

P 

 = arctg

Víi ký hiÖu nh trªn ta cã c¸c c«ng thøc tÝnh:

Q P

vµ m= (1.32)

Víi c¸c ký hiÖu (1.31), ta sÏ viÕt ®îc c¸c ph¬ng tr×nh sè hiÖu chØnh (1.30) ë

d¹ng:

iX = X 0 + x’ i P- y’ i Q- X i

iY = Y 0 + y’ i P+ x’ i Q- Y i

(1.33) V

Víi c¸ch ghÐp Èn sè nh vËy, chóng ta sÏ lËp hÖ ph¬ng tr×nh chuÈn cã 4

Èn sè lµ X 0 , Y 0 , P vµ Q.

HÖ ph¬ng tr×nh chuÈn cã d¹ng: CTCX+ CTL= 0 (1.34)

Trong ®ã C lµ ma trËn hÖ sè ph¬ng tr×nh sè hiÖu chØnh, X lµ vector Èn

Cao B¸ H¹

-21 -

Líp Tr¾c ®ÞaB-K48

sè, L lµ vector sè h¹ng tù do:

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

' 1

 

Y 0 P

     

     

1 0 0 1 . . 01 10

' x 1 ' y 1 . x ' ' y

y  ' x 1 . y  ' x

 

       

       

X Y 1 . X Y n

       

       

C= ; X= ; L=

Sau khi gi¶i hÖ ph¬ng tr×nh chuÈn (1.34), ta nhËn ®îc vector Èn sè X,

tõ ®ã sÏ tÝnh ®îc 4 tham sè chuyÓn ®æi gi÷a hai hÖ.

§é chÝnh x¸c cña c¸c Èn sè ®îc tÝnh trªn c¬ së sai sè trung ph¬ng ®¬n

 =

vÞ träng sè  , tÝnh theo c«ng thøc:

 4

 VV 2 n

(1.35)

Vµ ma trËn nghÞch ®¶o cña ma trËn hÖ sè ph¬ng tr×nh chuÈn:

Q= (C T C) 1 (1.36)

Bµi to¸n chuyÓn ®æi to¹ ®é nªu trªn ®îc gäi lµ phÐp chuyÓn ®æi to¹ ®é

Helmert. Qua bµi to¸n chuyÓn ®æi nµy cã thÓ ph¸t biÓu r»ng: phÐp chuyÓn ®æi

to¹ ®é Helmert lµ phÐp biÕn ®æi to¹ ®é ®ång d¹ng tõ hÖ nµy sang hÖ kh¸c.

Trong tr¾c ®Þa c«ng tr×nh, phÐp chuyÓn ®æi nµy ®îc sö dông ®Ó tÝnh

chuyÓn to¹ ®é tõ hÖ to¹ ®é c«ng tr×nh sang hÖ to¹ ®é quy íc ( hoÆc hÖ to¹ ®é

nhµ níc, ®Ó phôc vô cho c¸c môc ®Ých kh¸c nhau) vµ ngîc l¹i.

1.5. Líi khèng chÕ thi c«ng c«ng tr×nh

Líi khèng chÕ thi c«ng c«ng tr×nh lµ c¬ së tr¾c ®Þa ®Ó chuyÓn thiÕt kÕ

c«ng tr×nh ra thùc ®Þa, ®Ó bè trÝ chi tiÕt c«ng tr×nh vµ còng lµ c¬ së ®Ó ®o vÏ

hoµn c«ng c«ng tr×nh.

1.5.1. §Æc ®iÓm

So víi c¸c d¹ng líi tr¾c ®Þa dïng trong ®o vÏ b¶n ®å th× líi khèng chÕ

thi c«ng c«ng tr×nh cã nh÷ng ®Æc ®iÓm c¬ b¶n sau:

Cao B¸ H¹

-22 -

Líp Tr¾c ®ÞaB-K48

C¸c c«ng tr×nh x©y dùng thêng cã diÖn tÝch kh«ng lín, l¹i ph¶i bè trÝ nhiÒu h¹ng môc c«ng tr×nh nªn c¸c ®iÓm khèng chÕ ph¶i ®¶m b¶o yªu cÇu vÒ mËt ®é ®iÓm vµ ®é chÝnh x¸c cÇn thiÕt( vÞ trÝ vµ mËt ®é c¸c ®iÓm cña líi tuú

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

thuéc vµo ®Æc ®iÓm kü thuËt cña tõng lo¹i c«ng tr×nh) th× míi cã thÓ bè trÝ ®îc c¸c h¹ng môc c«ng tr×nh cã ®é chÝnh x¸c yªu cÇu tõ thÊp ®Õn cao.

Cã mét ®Æc ®iÓm lµ c¸c c«ng tr×nh ®îc x©y dùng trong mét thêi gian dµi vµ viÖc thi c«ng c¸c c«ng tr×nh x©y dùng ®îc tiÕn hµnh theo mét tr×nh tù x©y dùng nhÊt ®Þnh, theo tõng giai ®o¹n thi c«ng c«ng tr×nh. C«ng tr×nh x©y dùng ph¶i ®îc ®Þnh vÞ trong mét hÖ thèng to¹ ®é vµ ®é cao thèng nhÊt cña khu vùc x©y dùng c«ng tr×nh, ®ã lµ hÖ to¹ ®é c«ng tr×nh. ChÝnh v× vËy c¸c ®iÓm cña líi khèng chÕ thi c«ng sÏ ®îc sö dông nhiÒu lÇn nh»m ®¶m b¶o tÝnh thèng nhÊt cña sè liÖu bè trÝ còng nh ®¶m b¶o tÝnh chÝnh x¸c cña c¸c h¹ng môc c«ng tr×nh.

Qu¸ tr×nh thi c«ng diÔn ra trong thêi gian dµi sÏ lµm líi khèng chÕ thi c«ng c«ng tr×nh dÔ bÞ ph¸ huû. V× vËy, ph¶i ®¶m b¶o ®é æn dÞnh cña c¸c ®iÓm trong líi vµ cã kÕ ho¹ch b¶o qu¶n chóng trong thêi gian dµi.

ViÖc bè trÝ c«ng tr×nh thêng ®îc tiÕn hµnh theo ba giai ®o¹n( bè trÝ c¬ b¶n, bè trÝ chi tiÕt vµ bè trÝ c«ng nghÖ). V× vËy, líi thi c«ng c«ng tr×nh ph¶i ®îc thµnh lËp qua mét sè bËc vµ nhÊt thiÕt ph¶i ®îc tÝnh to¸n trong cïng mét hÖ thèng täa ®é ®· lùa chän tríc ®©y, trong giai ®o¹n kh¶o s¸t c«ng tr×nh. VÞ trÝ, mËt ®é vµ sè lîng ®iÓm cña líi thi c«ng sÏ tïy thuéc yªu cÇu vµ ®Æc ®iÓm kü thuËt cña tõng lo¹i c«ng tr×nh. VÝ dô: líi thi c«ng cÇu ph¶i cã hai ®iÓm n»m trªn híng trôc cÇu, líi khèng chÕ mÆt b»ng trªn mÆt ®Êt trong thi c«ng x©y dùng ®êng hÇm ph¶i cã hai ®iÓm gÇn cöa hÇm ®Ó chuyÒn to¹ ®é vµ ph¬ng vÞ xuèng hÇm…

§é chÝnh x¸c cña líi thi c«ng c«ng tr×nh tuú thuéc vµo lo¹i c«ng tr×nh. ViÖc íc tÝnh ®é chÝnh x¸c cña líi ®îc tiÕn hµnh theo ph¬ng ph¸p líi tr¾c ®Þa tù do do b¶n chÊt cña líi khèng chÕ thi c«ng cã ®é chÝnh x¸c bËc sau cao h¬n bËc tríc.

1.5.2. Mét sè d¹ng líi ®Æc trng

Ngoµi nh÷ng ®Æc ®iÓm chung th× ®èi víi mçi d¹ng c«ng tr×nh, líi khèng

chÕ thi c«ng l¹i cã nh÷ng ®Æc thï riªng thÓ hiÖn ë mét sè d¹ng c«ng tr×nh tiªu

Cao B¸ H¹

-23 -

Líp Tr¾c ®ÞaB-K48

biÓu sau ®©y:

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

1.5.2.1. Líi thi c«ng ®êng hÇm

§èi víi mét tuyÕn ®êng hÇm, thêng thµnh lËp chuçi tam gi¸c, ®o hai c¹nh ®¸y ë hai ®Çu chuçi hoÆc chuçi tam gi¸c ®o gãc - c¹nh kÕt hîp. §Ó chuyÒn täa ®é vµ ph¬ng vÞ xuèng hÇm, cÇn ph¶i cã ®iÓm cña líi khèng chÕ ë gÇn miÖng giÕng ®øng vµ cöa hÇm. Víi ®Æc ®iÓm nh vËy nªn thêng thµnh lËp 3 bËc líi:

- Líi khèng chÕ c¬ së: môc ®Ých t¹o ra hÖ täa ®é thèng nhÊt ®Ó thi c«ng.

- §o nèi tõ c¸c ®iÓm c¬ së vµo cöa hÇm, thêng thµnh lËp theo ph¬ng

ph¸p ®a gi¸c: môc ®Ých truyÒn täa ®é vµo cöa hÇm.

- Líi ®a gi¸c ®êng hÇm: ®îc thµnh lËp trong qu¸ tr×nh thi c«ng hÇm.

Líi thi c«ng ®êng hÇm ph¶i ®¶m b¶o sai sè híng ngang ®µo th«ng

hÇm n»m trong giíi h¹n cho phÐp.

KC6

KC5

KC4

§å h×nh

H1

KC1

KC2

KC3

H×nh 1.6 S¬ ®å líi thi c«ng ®êng hÇm

1.5.2.2. Líi thi c«ng c«ng tr×nh cÇu

Cao B¸ H¹

-24 -

Líp Tr¾c ®ÞaB-K48

Líi thi c«ng cÇu lµ líi phôc vô cho qu¸ tr×nh x©y dùng cÇu: bè trÞ trô cÇu, mè cÇu, nhÞp cÇu… vµ dïng ®Ó quan tr¾c chuyÓn dÞch ngang c«ng tr×nh cÇu. §å h×nh c¬ b¶n cña líi thêng lµ tø gi¸c tr¾c ®Þa ®¬n hoÆc kÐp. Mét hoÆc hai c¹nh ®¸y ®îc ®o víi ®é chÝnh x¸c 1:200000  1:300000; gãc ®o víi ®é chÝnh x¸c m = 1 2”. §èi víi líi thi c«ng cÇu th× ph¶i ®¶m b¶o sai sè theo híng däc cña cÇu.

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

H×nh 1.7 S¬ ®å líi thi c«ng cÇu

1.5.2.3. Líi « vu«ng x©y dùng

B 2

C3 H×nh 1.8 S¬ ®å líi « vu«ng x©y dùng

Líi « vu«ng x©y dùng ®îc lËp víi môc ®Ých ®Ó chuyÓn b¶n thiÕt kÕ c«ng tr×nh c«ng nghiÖp ra thùc ®Þa, th«ng thêng x©y dùng c¬ së khèng chÕ täa ®é ë d¹ng ®Æc biÖt bao gåm mét hÖ thèng dµy ®Æc c¸c ®iÓm mèc tr¾c ®Þa ph©n bè mét c¸ch t¬ng ®èi ®ång ®Òu trªn toµn bé khu vùc. C¸c ®iÓm nµy t¹o thµnh mét m¹ng líi c¸c h×nh vu«ng hay h×nh ch÷ nhËt cã c¸c c¹nh song song víi trôc chÝnh cña c«ng tr×nh. §å h×nh:

1.5.2.4. C«ng tr×nh thuû lîi - thuû ®iÖn

C«ng tr×nh thñy ®iÖn lµ mét tæ hîp c¸c c«ng tr×nh x©y dùng rÊt phøc t¹p,

bao gåm ®Ëp thuû ®iÖn, nhµ m¸y ®iÖn, ©u thuyÒn, kªnh dÉn níc, c¸c ®êng

hÇm thuû lîi..., gi÷a chóng tån t¹i mèi quan hÖ h×nh häc chÆt chÏ c¶ vÒ

Cao B¸ H¹

-25 -

Líp Tr¾c ®ÞaB-K48

ph¬ng diÖn mÆt b»ng vµ ®é cao.

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

TC2

TC3

TC1

TC4

TC7

TC6

TC8

TC5

§å h×nh

H×nh 1.9 Mét s¬ ®å líi khèng chÕ thñy c«ng - thñy ®iÖn

1.5.2.5. Líi thi c«ng c«ng tr×nh d©n dông

§èi víi c«ng tr×nh d©n dông líi thi c«ng thêng ®îc thiÕt kÕ theo h×nh

d¹ng c«ng tr×nh. Víi líi thi c«ng (h×nh 1.10) lµ m¹ng líi khèng chÕ trôc

c«ng tr×nh d©n dông, líi ®îc x©y dùng gåm 8 ®iÓm míi A1, A2, A3, A4,

A5, A6, A8, A9 vµ 9 ®iÓm khèng chÕ T-5, T-9, T-B’, T-B, T-H’, T-H, T-M, T-

5’, T-9’ ®îc cho díi d¹ng dÊu trôc trªn têng.

T-B

§å h×nh T-5 T-9

T-B’

T-H’ T-H

T-M

T-5’ T-9’

Cao B¸ H¹

-26 -

Líp Tr¾c ®ÞaB-K48

H×nh 1.10 Mét s¬ ®å líi thi c«ng c«ng tr×nh d©n dông

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

1.5.3. Nguyªn t¾c x©y dùng líi

Líi thi c«ng ®îc thµnh lËp b»ng c¸c ph¬ng ph¸p tam gi¸c, ®a gi¸c vµ

mét sè ph¬ng ph¸p ®Æc trng trong tr¾c ®i¹ c«ng tr×nh: ph¬ng ph¸p tø gi¸c

kh«ng ®êng chÐo, líi « vu«ng x©y dùng…Yªu cÇu ®é chÝnh x¸c vµ ®å h×nh

líi ®îc tÝnh to¸n, lùa chän trªn c¬ së ®¸p øng c¸c chØ tiªu cña c«ng t¸c bè

trÝ c«ng tr×nh vµ ®o vÏ hoµn c«ng. Th«ng thêng líi thi c«ng c«ng tr×nh lµ hÖ

thèng líi nhiÒu bËc, yªu cÇu ®é chÝnh x¸c víi mçi bËc líi t¨ng dÇn vµ ph¶i

®îc thµnh lËp trong cïng hÖ trôc täa ®é, ®é cao thèng nhÊt ®· ®îc lùa chän

®èi víi tõng c«ng tr×nh. V× vËy líi thi c«ng ph¶i ®îc x©y dùng theo nh÷ng

nguyªn t¾c sau:

1. Líi thi c«ng lµ m¹ng líi ®éc lËp côc bé (®Ó tr¸nh ¶nh hëng sai sè sè liÖu

gèc).

2. Quy m« kÝch thíc líi ®îc x©y dùng “tõ tæng thÓ ®Õn côc bé”, ®ång thêi

yªu cÇu ®é chÝnh x¸c tíi tõng bËc líi lµ t¨ng dÇn (líi bËc sau cã ®é chÝnh

x¸c cao h¬n líi bËc tríc).

3. TÊt c¶ c¸c bËc líi thi c«ng ph¶i ®îc tÝnh täa ®é trong mét hÖ thèng nhÊt,

®· ®îc lùa chän trong giai ®o¹n thi c«ng c«ng tr×nh.

4. Trong mét sè trêng hîp líi thi c«ng ®îc thiÕt kÕ tèi u ®é chÝnh x¸c

theo híng ®· ®Þnh tríc phï hîp víi yªu cÇu kü thuËt c«ng tr×nh.

Nh÷ng nguyªn t¾c nªu trªn ®¶m b¶o cho líi thi c«ng kh«ng bÞ biÕn d¹ng do

¶nh hëng sai sè sè liÖu gèc, ®ång thêi líi ®îc ®Þnh vÞ trong cïng mét hÖ

trôc täa ®é chung. Nh vËy vÒ b¶n chÊt líi thi c«ng c«ng tr×nh lµ mét d¹ng

Cao B¸ H¹

-27 -

Líp Tr¾c ®ÞaB-K48

líi tr¾c ®Þa tù do, vÊn ®Ò nµy ®îc ®Ò cËp ë phÇn sau.

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

Ch¬ng 2

Kh¶o s¸t ph¬ng ph¸p b×nh sai líi tù do

2.1. Kh¸i niÖm chung vÒ líi tr¾c ®Þa tù do

2.1.1. §Þnh nghÜa, ph©n lo¹i líi tù do

Tuú thuéc vµo tÝnh chÊt sè liÖu gèc mµ m¹ng líi tr¾c ®Þa ®îc chia

thµnh 2 lo¹i lµ líi phô thuéc vµ líi tù do.

2.1.1.1. Líi phô thuéc

Líi phô thuéc lµ líi cã thõa sè liÖu gèc ®Õ x¸c ®Þnh h×nh d¹ng, kÝch

thíc vµ ®Þnh vÞ líi trong mét hÖ to¹ ®é nµo ®ã. §èi víi líi mÆt b»ng sè

lîng tèi thiÓu vÒ sè liÖu gèc lµ bèn yÕu tè, gåm:

- Mét cÆp täa ®é (X,Y) ®Ó ®Þnh vÞ líi.

- Mét chiÒu dµi c¹nh ®Ó x¸c ®Þnh kÝch thíc líi.

- Mét gãc ph¬ng vÞ ®Ó ®Þnh híng líi.

§èi víi líi tr¾c ®Þa kh«ng gian sè lîng tèi thiÓu vÒ sè liÖu gèc lµ 7 yÕu tè

gåm 3 gi¸ trÞ täa ®é: X, Y, Z; 3 gãc xoay: k, ,  vµ chiÒu dµi mét c¹nh.

2.1.1.2. Líi tù do

Mét c¸ch chung nhÊt, líi tr¾c ®Þa tù do ®îc ®Þnh nghÜa lµ lo¹i líi mµ

trong ®ã kh«ng cã ®ñ sè liÖu gèc tèi thiÓu cÇn thiÕt cho viÖc ®Þnh vÞ, nÕu líi

tr¾c ®Þa mµ sè liÖu gèc cã sai sè vît qu¸ sai sè ®o th× m¹ng líi còng ®îc

coi lµ líi tù do, trong trêng hîp nµy sè liÖu gèc chØ cã t¸c dông lµ c¬ së cho

viÖc ®Þnh vÞ líi.

Nh vËy cã thÓ rót ra nh÷ng ®Þnh nghÜa cô thÓ h¬n líi tr¾c ®Þa tù do nh sau:

“líi tr¾c ®Þa tù do lµ líi thiÕu toµn bé hoÆc thiÕu mét sè trong nhãm yÕu tè

gèc tèi thiÓu lµ: mét cÆp täa ®é (X, Y), mét gãc ph¬ng vÞ, mét c¹nh ®¸y(víi

líi mÆt b»ng), ®é cao(H) (víi líi ®é cao) ”. Trong líi tr¾c ®Þa tù do sè

lîng c¸c yÕu tè gèc cßn thiÕu ®îc gäi lµ sè khuyÕt cña líi vµ ®îc ký hiÖu

Cao B¸ H¹

-28 -

Líp Tr¾c ®ÞaB-K48

b»ng d, cßn b¶n th©n líi ®îc gäi lµ líi tù do bËc d.

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

Tõ c¸c kh¸i niÖm trªn suy ra hai trêng hîp sau :

- Líi tù do kh«ng cã sè khuyÕt (d = 0): lµ líi cã sè liÖu gèc tèi thiÓu

võa ®ñ ®Ó x¸c ®Þnh h×nh d¹ng, kÝch thíc vµ ®Þnh vÞ líi trong mét hÖ to¹ ®é,

líi nµy cßn cã tªn gäi lµ líi tù do bËc kh«ng.

- Líi tù do cã sè khuyÕt (d > 0): lµ líi thiÕu sè liÖu gèc tèi thiÓu cÇn

thiÕt cho viÖc ®Þnh vÞ, sè khuyÕt d cã thÓ nhËn c¸c gi¸ trÞ (1, 2, 3, 4), t¬ng

øng bËc tù do cña líi lµ (1, 2, 3, 4). §Ó tiÖn ph©n biÖt møc ®é vµ d¹ng tù do

cña líi cã thÓ chia líi mÆt b»ng tù do thµnh c¸c lo¹i sau:

a. Líi tù do bËc 1(d = 1): líi thiÕu mét c¹nh hoÆc mét ph¬ng vÞ khëi tÝnh

hoÆc to¹ ®é X hoÆc to¹ ®é Y.

b. Líi tù do bËc 2 (d = 2): cã c¸c trêng hîp sau:

- Líi thiÕu mét cÆp täa ®é gèc (X, Y)

- Líi thiÕu to¹ ®é X, mét c¹nh ®¸y hoÆc to¹ ®é X vµ mét ph¬ng vÞ

- Líi thiÕu to¹ ®é Y, mét c¹nh ®¸y hoÆc to¹ ®é Y vµ mét ph¬ng vÞ

- Líi thiÕu mét c¹nh ®¸y vµ mét ph¬ng vÞ.

c. Líi tù do bËc 3 (d = 3): cã c¸c trêng hîp sau:

- Líi thiÕu mét cÆp täa ®é gèc (X, Y), mét gãc ®Þnh híng.

- Líi thiÕu mét cÆp täa ®é gèc (X, Y), mét c¹nh ®¸y.

- Líi thiÕu to¹ ®é X, mét c¹nh ®¸y vµ mét ph¬ng vÞ.

- Líi thiÕu to¹ ®é Y, mét c¹nh ®¸y vµ mét ph¬ng vÞ.

d. Líi tù do bËc 4 (d = 4): líi thiÕu tÊt c¶ c¸c yÕu tè ®Þnh vÞ (X,Y,, m)

Do cã m« h×nh b×nh sai thuËn tiÖn cho viÖc lËp tr×nh ®Ó cã thÓ tù ®éng ho¸

xö lý trªn m¸y tÝnh ®iÖn tö, l¹i cã kh¶ n¨ng linh ho¹t trong kh©u chän lùa ®iÒu

kiÖn ®Þnh vÞ líi nªn lý thuyÕt b×nh sai líi tù do ngµy nay cµng ®îc khai

th¸c ®Ó øng dông s©u h¬n trong nhiÒu lÜnh vùc cña tr¾c ®Þa. M« h×nh to¸n häc

cña ph¬ng ph¸p b×nh sai líi tù do ®îc thÓ hiÖn cô thÓ nh ë phÇn sau.

2.1.2. M« h×nh to¸n häc cña ph¬ng ph¸p b×nh sai líi tù do

Cao B¸ H¹

-29 -

Líp Tr¾c ®ÞaB-K48

Chóng ta xem xÐt m« h×nh to¸n häc cña ph¬ng ph¸p b×nh sai líi tr¾c ®Þa tù

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

do trªn c¬ së cña bµi to¸n b×nh sai gi¸n tiÕp kÌm ®iÒu kiÖn.

Gi¶ sö mét m¹ng líi tù do ®îc b×nh sai theo ph¬ng ph¸p gi¸n tiÕp, sÏ x¸c

®Þnh ®îc:

1. LËp hÖ ph¬ng tr×nh sè hiÖu chØnh

(2. 1) V = AX + L

trong ®ã: A - Ma trËn hÖ sè hÖ ph¬ng tr×nh sè hiÖu chØnh

X - Vector Èn sè

V , L - Vector sè hiÖu chØnh vµ vector sè h¹ng tù do

Do líi thiÕu sè liÖu gèc nªn trong ma trËn A cã c¸c cét phô thuéc, sè lîng

cét phô thuéc nµy b»ng sè khuyÕt cña líi

2. LËp hÖ ph¬ng tr×nh chuÈn

Theo nguyªn lý cña ph¬ng ph¸p sè b×nh ph¬ng nhá nhÊt, tõ hÖ ph¬ng tr×nh

sè hiÖu chØnh (2. 1) lËp ®îc hÖ ph¬ng tr×nh chuÈn:

RX + b = 0 (2. 2)

T PAAR T PLAb

 

  

Víi

Do líi thiÕu sè liÖu gèc tèi thiÓu nªn hÖ (2. 2) cã ®Æc ®iÓm sau:

- Det(R) = 0 suy ra hÖ cã v« sè nghiÖm.

- Kh«ng tån t¹i phÐp nghÞch ®¶o ma trËn R.

Víi ®Æc ®iÓm nh vËy nªn kh«ng thÓ gi¶i hÖ theo c¸c ph¬ng ph¸p th«ng

thêng ®îc. §Ó cã thÓ gi¶i ®îc cÇn ®a vµo mét hÖ ®iÒu kiÖn rµng buéc c¸c

vector Èn sè.

HÖ ®iÒu kiÖn rµng buéc vector Èn sè cã d¹ng:

(2. 3)

CTX + LC = 0 trong ®ã: CT - Ma trËn hÖ sè ®Þnh vÞ

X, Lc - Vector Èn sè, vector sè h¹ng tù do; thêng chän Lc= 0.

HÖ ®iÒu kiÖn (2. 3) ph¶i tháa m·n

Cao B¸ H¹

-30 -

Líp Tr¾c ®ÞaB-K48

- Sè lîng ®iÒu kiÖn b»ng sè khuyÕt d trong líi

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

- C¸c hµng cña ma trËn CT ph¶i ®éc lËp tuyÕn tÝnh víi c¸c cét cña ma trËn A.

3. LËp hÖ ph¬ng tr×nh chuÈn më réng

Trªn c¬ së cña ph¬ng ph¸p b×nh sai gi¸n tiÕp kÌm ®iÒu kiÖn, kÕt hîp biÓu

thøc (2. 2) vµ (2. 3) x¸c ®Þnh ®îc hÖ ph¬ng tr×nh chuÈn më réng

b  0



RX   T XC 

(2. 4)

HÖ ph¬ng tr×nh (2. 4) ®îc biÓu diÔn díi d¹ng ma trËn khèi

CR T

  C 

  

  

  

b   

  

(2. 5)

HÖ (2. 5) cã ma trËn hÖ sè kh«ng suy biÕn n÷a nªn tån t¹i ma trËn nghÞch ®¶o

1 

thêng:

CR T

  C 

  

  T 

  

(2. 6)

1

(

)







BCBT (



Trong ®ã R~ lµ ma trËn gi¶ nghÞch ®¶o cña R ®îc x¸c ®Þnh theo c«ng thøc:

víi

Vector nghiÖm cña hÖ ph¬ng tr×nh (2. 5) theo c«ng thøc:

(2. 7) X = -R~.b

4. §¸nh gi¸ ®é chÝnh x¸c



- Sai sè trung ph¬ng ®¬n vÞ träng sè

V T PV kn 

(2. 8)

n - k + d: sè lîng trÞ ®o thõa trong líi



mm 

- Sai sè vÞ trÝ ®iÓm

2 x

2 y



~ R



(2. 9)

~ R xx

; víi

Cao B¸ H¹

-31 -

Líp Tr¾c ®ÞaB-K48

- Sai sè trung ph¬ng cña hµm sè

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp



1 P F

fRf



(2. 10)

1 p

víi (2. 11)

: lµ vector hÖ sè khai triÓn trong hµm sè cÇn ®¸nh gi¸

Qua kh¶o s¸t bµi to¸n b×nh sai líi tù do chóng t«i nhËn thÊy r»ng: b×nh

sai líi tù do thùc chÊt lµ bµi to¸n b×nh sai gi¸n tiÕp kÌm ®iÒu kiÖn gåm hai

qu¸ tr×nh lµ xö lý vector trÞ ®o cña líi (quy tr×nh nµy ®îc thùc hiÖn theo

nguyªn lý sè b×nh ph¬ng nhá nhÊt ®èi víi vector sè hiÖu chØnh trÞ ®o) vµ ®Þnh

vÞ líi (biÓu thøc (2. 3) lµ ®iÒu kiÖn ®Þnh vÞ líi).

2.2. §Þnh vÞ líi

Tõ kh¸i niÖm vÒ b×nh sai líi tù do vµ m« h×nh cña bµi to¸n, thÊy r»ng

“®Þnh vÞ líi chÝnh lµ qu¸ tr×nh x¸c ®Þnh vÞ trÝ, h×nh d¹ng, kÝch thíc, ph¬ng

híng cña líi theo mét tiªu chuÈn ®Þnh vÞ nµo ®ã ”.

So s¸nh m« h×nh cña bµi to¸n b×nh sai líi tù do víi c¸c bµi to¸n b×nh sai

kh¸c theo nguyªn lý cña ph¬ng ph¸p sè b×nh ph¬ng nhá nhÊt, chóng t«i rót

ra c¸c nhËn xÐt sau:

Trong bµi to¸n b×nh sai ®iÒu kiÖn còng nh b×nh sai gi¸n tiÕp víi sè liÖu

gèc, tËp hîp sè liÖu gèc tham gia vµo qu¸ tr×nh b×nh sai m¹ng líi. KÕt qu¶

b×nh sai v× thÕ chÞu ¶nh hëng cña sai sè sè liÖu gèc vµ nh÷ng chuyÓn dÞch

(nÕu cã) cña c¸c sè liÖu gèc.

Gi¶i ph¸p b×nh sai líi tù do bËc 0 vµ b×nh sai cã tÝnh ®Õn ¶nh hëng sai

sè cña sè liÖu gèc sÏ lo¹i trõ ®îc ¶nh hëng sai sè cña sè liÖu gèc.

Trong bµi to¸n b×nh sai líi tr¾c ®Þa tù do, tËp hîp sè liÖu gèc chØ tham

gia vµo qu¸ tr×nh ®Þnh vÞ mµ kh«ng tham gia vµo qu¸ tr×nh b×nh sai, v× vËy

vector trÞ b×nh sai nhËn ®îc kh«ng chÞu ¶nh hëng cña sai sè sè liÖu gèc vµ

nh÷ng chuyÓn dÞch (nÕu cã) cña c¸c sè liÖu gèc. §©y lµ mét ®Æc ®iÓm rÊt quan

Cao B¸ H¹

-32 -

Líp Tr¾c ®ÞaB-K48

träng, cho thÊy tÝnh u viÖt cña ph¬ng ph¸p b×nh sai líi tù do so víi c¸c

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

ph¬ng ph¸p b×nh sai th«ng thêng. §Æc ®iÓm nµy ®îc chóng t«i khai th¸c

øng dông trong vÊn ®Ò ®Þnh vÞ hÖ thèng líi khèng chÕ thi c«ng c«ng tr×nh.

Nh ®· nãi ë tiÕt 1.5, do b¶n chÊt líi thi c«ng c«ng tr×nh cã ®é chÝnh

x¸c bËc sau cao h¬n bËc tríc, mÆt kh¸c qu¸ tr×nh thi c«ng diÔn ra l©u dµi,

theo tõng giai ®o¹n do vËy, líi thi c«ng c«ng tr×nh thêng lËp qua nhiÒu bËc.

BËc líi c¬ së cã t¸c dông lµm gèc khëi tÝnh cho c¶ hÖ thèng, nÕu nh tËp hîp

c¸c ®iÓm gèc lµ tuyÖt ®èi æn ®Þnh th× to¹ ®é (®é cao) c¸c ®iÓm cÊp sau sÏ ®îc

x¸c ®Þnh theo c¸c ®iÓm gèc cÊp c¬ së, khi ®ã gi¶i ph¸p b×nh sai gi¸n tiÕp víi

sè liÖu gèc cã thÓ ®îc chÊp nhËn. Tuy nhiªn, trong qu¸ tr×nh thi c«ng khã cã

thÓ ®¶m b¶o r»ng c¸c ®iÓm gèc (to¹ ®é vµ ®é cao) l¹i kh«ng bÞ thay ®æi gi¸ trÞ.

§iÒu ®ã cã nghÜa lµ m¹ng líi khèng chÕ thi c«ng c«ng tr×nh cã thÓ kh«ng æn

®Þnh, chóng cã b¶n chÊt lµ líi tù do. Gi¶i ph¸p b×nh sai gi¸n tiÕp víi sè liÖu

gèc trong trêng hîp nµy kh«ng cßn phï hîp. V× vËy cÇn ¸p dông thuËt to¸n

b×nh sai líi tù do cho d¹ng líi nµy.

VËn dông m« h×nh b×nh sai líi tù do cho líi thi c«ng c«ng tr×nh, vÊn

®Ò ®Þnh vÞ líi cã thÓ ®îc lùa chän nh sau:

§iÒu kiÖn ®Þnh vÞ (2.3) ®îc x¸c ®Þnh:

Tõ ma trËn C= (c1 c2 c3 … cn)T :

' x i y



' y i ' x i

' i

01   10 

  

0000

®èi víi c¸c ®iÓm líi c¬ së vµ Víi líi mÆt b»ng ta chän ci =

0000

  

  

®èi víi c¸c ®iÓm kh¸c. ci =

Víi líi ®é cao ta chän ci=1 ®èi víi c¸c ®iÓm líi c¬ së vµ ci= 0 ®èi víi c¸c ®iÓm kh¸c.

2.3. Mét sè tÝnh chÊt c¬ b¶n cña kÕt qu¶ b×nh sai líi tù do

§Ó kiÓm chøng thuËt to¸n vµ c¸c tÝnh chÊt cña ph¬ng ph¸p b×nh sai líi tù do

Cao B¸ H¹

-33 -

Líp Tr¾c ®ÞaB-K48

chóng ta xÐt bµi to¸n b×nh sai líi mÆt b»ng thi c«ng thuû ®iÖn S«ng Hinh, sè

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

liÖu ®îc cho theo nguyªn t¾c m· ho¸ cña ch¬ng tr×nh BuildNet ®· ®îc

LUOI THI CONG THUY DIEN SONG HINH DO THANG 6-1996

4 4 25 12 0 0.01 1.6 0 .007 .000003 TC-2 TC-6 TC-8 TC-4 TC-5 TC-3 TC-1 TC-7 1 1430267.792 277344.183 2 1429502.218 276873.885 3 1428889.965 277877.683 4 1429299.983 277996.042 5 1428937.265 277222.534 6 1430047.649 277817.560 1 7 6 51 52 9.54 6 7 4 78 40 37.16 4 7 5 75 18 35.2 5 7 2 58 47 22.0 7 2 5 72 25 47.2 1 8 7 24 19 57.31 7 8 2 24 52 13.76 5 3 4 101 58 24.96 1 7 630.589 7 6 552.190 7 4 654.023 7 5 740.025 7 2 583.878 3 4 426.757 3 5 656.858 5 4 854.348 5 2 663.880

chóng t«i lËp nh giíi thiÖu ë ch¬ng 3:

§å h×nh:

Cao B¸ H¹

-34 -

Líp Tr¾c ®ÞaB-K48

H×nh 2.6. Líi khèng chÕ thi c«ng thuû ®iÖn S«ng Hinh

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

Trêng hîp 1: líi ®îc ®Þnh vÞ víi 4 c¸c ®iÓm nót: TC-7, TC-3, TC-1, TC-5.

================================================================================== | .000 .000 .000 .000 .000 .000 .000 .000 .500 .000 .500 .000 .500 .000 .500 .000| CT=| .000 .000 .000 .000 .000 .000 .000 .000 .000 .500 .000 .500 .000 .500 .000 .500| | .000 .000 .000 .000 .000 .000 .000 .000-.002 .549 .378-.160 .137 .098-.514-.487| ==================================================================================

IV.KET QUA TRI DO SAU BINH SAI ==============================

A.TRI DO GOC NGANG SAU BINH SAI

===================================================================== | SO | TEN-DINH | GIA TRI GOC | HIEU | TRI GOC SAU | | THU|---------------------| DO | CHINH | BINH SAI | | TU | Trai-Giua-Phai | Do-Phut-Giay| Giay | Do-Phut-Giay| |----|---------------------|-------------|------------|-------------| | 1 |TC-5 TC-1 TC-3 | 51 52 9.54| .75 | 51 52 10.29| | 2 |TC-3 TC-1 TC-4 | 78 40 37.16| 1.31 | 78 40 38.47| | 3 |TC-4 TC-1 TC-5 | 75 18 35.20| 1.35 | 75 18 36.55| -.80 | 58 47 21.20| | 4 |TC-5 TC-1 TC-6 | 58 47 22.00| -.13 | 56 4 16.64| | 5 |TC-6 TC-1 TC-7 | 56 4 16.77| | 6 |TC-7 TC-1 TC-5 | 39 16 57.69| -.84 | 39 16 56.85| | 7 |TC-3 TC-5 TC-1 | 56 18 18.23| .97 | 56 18 19.20| | 8 |TC-1 TC-5 TC-6 | 40 19 1.42| .07 | 40 19 1.49| | 9 |TC-6 TC-5 TC-7 | 76 4 2.69| .40 | 76 4 3.09| .65 | 41 36 44.21| |10 |TC-4 TC-3 TC-5 | 41 36 43.56| |11 |TC-5 TC-3 TC-1 | 14 55 41.00| 3.48 | 14 55 44.48| |12 |TC-1 TC-3 TC-5 | 71 49 29.60| .91 | 71 49 30.51| |13 |TC-8 TC-4 TC-5 | 48 46 25.35| 2.26 | 48 46 27.61| |14 |TC-5 TC-4 TC-1 | 56 54 56.31| .16 | 56 54 56.47| -.91 | 44 46 52.84| |15 |TC-1 TC-4 TC-3 | 44 46 53.75| -.29 | 48 46 51.84| |16 |TC-6 TC-5 TC-1 | 48 46 52.13| -.92 | 11 5 .50| |17 |TC-1 TC-5 TC-3 | 11 5 1.42| |18 |TC-3 TC-5 TC-4 | 36 41 27.16| -.69 | 36 41 26.47| |19 |TC-4 TC-5 TC-8 | 29 15 1.87| 3.01 | 29 15 4.88| TC-6 TC-5 | 54 43 43.68| .93 | 54 43 44.61| |20 |TC-7 -.42 | 44 19 45.03| |21 |TC-5 TC-6 TC-1 | 44 19 45.45| -.24 | 72 25 46.96| |22 |TC-1 TC-6 TC-5 | 72 25 47.20| | 24 19 57.31| 1.27 | 24 19 58.58| |23 |TC-5 TC-7 TC-1 |24 |TC-1 TC-7 TC-6 | 24 52 13.76| -.04 | 24 52 13.72| |25 |TC-5 TC-8 TC-4 | 101 58 24.96| 2.55 | 101 58 27.51| =====================================================================

B.TRI DO CANH SAU BINH SAI

=========================================================== | SO | TEN-CANH | CHIEU DAI | HIEU | CHIEU DAI | | THU|----------------| DO | CHINH | SAU BINH SAI | | TU | DAU-CUOI | (m) | (m) | (m) | |----|----------------|------------|-------|--------------| | 1 |TC-5 TC-1 | 630.589 | .000 | 630.589 | | 2 |TC-1 TC-3 | 552.190 | .014 | 552.204 | | 3 |TC-1 TC-4 | 654.023 | -.002 | 654.021 | | 4 |TC-1 TC-5 | 740.025 | -.009 | 740.016 | | 5 |TC-1 TC-6 | 583.878 | .000 | 583.878 | | 6 |TC-1 TC-7 | 1370.990 | .002 | 1370.992 | | 7 |TC-5 TC-3 | 522.073 | -.001 | 522.072 | | 8 |TC-5 TC-7 | 968.974 | -.002 | 968.972 | | 9 |TC-5 TC-4 | 854.348 | -.005 | 854.343 | |10 |TC-5 TC-6 | 663.880 | .003 | 663.883 | |11 |TC-8 TC-4 | 426.757 | -.003 | 426.754 | |12 |TC-8 TC-5 | 656.858 | .003 | 656.861 | ===========================================================

Cao B¸ H¹

-35 -

Líp Tr¾c ®ÞaB-K48

KÕt qu¶ thu ®îc trong qu¸ tr×nh tÝnh to¸n xö lý:

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

V.KET QUA TOA DO DIEM SAU BINH SAI

==================================

===================================================================== | S | TEN | TOA DO | SAI SO VI TRI DIEM | | T | |-------------------------------|---------------------- | | T | DIEM | X(m) | Y(m) | Mx(cm)| My(cm)| Md(cm)| |---|-------|---------------|---------------|-------|-------|-------| | 1 |TC-5 | 1430267.790| 277344.178| .34 | .25 | .42 | | 2 |TC-6 | 1429502.223| 276873.891| .30 | .32 | .44 | | 3 |TC-8 | 1428889.973| 277877.692| .52 | .45 | .69 | | 4 |TC-4 | 1429299.985| 277996.052| .41 | .37 | .55 | | 5 |TC-5 | 1428937.255| 277222.534| .37 | .23 | .43 | | 6 |TC-3 | 1430047.649| 277817.567| .25 | .32 | .40 | | 7 |TC-1 | 1429644.548| 277440.157| .18 | .17 | .25 | | 8 |TC-7 | 1430561.260| 276420.716| .38 | .39 | .54 | =====================================================================

1. Sai so trung phuong trong so don vi mo = .96 "

Trêng hîp 2: líi ®îc ®Þnh vÞ theo 3 ®iÓm nót TC-1, TC-5, TC-3 (c¸c

bíc ®îc thùc hiÖn gièng nh trêng hîp 1).

================================================================================== | .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .577 .000 .577 .000 .577 .000| CT=| .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .577 .000 .577 .000 .577| | .000 .000 .000 .000 .000 .000 .000 .000 .000 .000 .359-.559-.059-.112-.300 .672| ==================================================================================

IV.KET QUA TRI DO SAU BINH SAI

===============================

A.TRI DO GOC NGANG SAU BINH SAI

===================================================================== | SO | TEN-DINH | GIA TRI GOC | HIEU | TRI GOC SAU | | THU|---------------------| DO | CHINH | BINH SAI | | TU | Trai-Giua-Phai | Do-Phut-Giay| Giay | Do-Phut-Giay| |----|---------------------|-------------|------------|-------------| | 1 |TC-3 TC-1 TC-3 | 51 52 9.54| .75 | 51 52 10.29| | 2 |TC-3 TC-1 TC-4 | 78 40 37.16| 1.31 | 78 40 38.47| | 3 |TC-4 TC-1 TC-5 | 75 18 35.20| 1.35 | 75 18 36.55| -.80 | 58 47 21.20| | 4 |TC-5 TC-1 TC-6 | 58 47 22.00| -.13 | 56 4 16.64| | 5 |TC-6 TC-1 TC-7 | 56 4 16.77| | 6 |TC-7 TC-1 TC-3 | 39 16 57.69| -.84 | 39 16 56.85| | 7 |TC-3 TC-3 TC-1 | 56 18 18.23| .97 | 56 18 19.20| | 8 |TC-1 TC-3 TC-6 | 40 19 1.42| .07 | 40 19 1.49| | 9 |TC-6 TC-3 TC-7 | 76 4 2.69| .40 | 76 4 3.09| |10 |TC-4 TC-3 TC-5 | 41 36 43.56| .65 | 41 36 44.21| |11 |TC-5 TC-3 TC-1 | 14 55 41.00| 3.48 | 14 55 44.48| |12 |TC-1 TC-3 TC-3 | 71 49 29.60| .91 | 71 49 30.51| |13 |TC-8 TC-4 TC-5 | 48 46 25.35| 2.26 | 48 46 27.61| |14 |TC-5 TC-4 TC-1 | 56 54 56.31| .16 | 56 54 56.47| -.91 | 44 46 52.84| |15 |TC-1 TC-4 TC-3 | 44 46 53.75| -.29 | 48 46 51.84| |16 |TC-6 TC-5 TC-1 | 48 46 52.13| -.92 | 11 5 |17 |TC-1 TC-5 TC-3 | 11 5 1.42| .50| |18 |TC-3 TC-5 TC-4 | 36 41 27.16| -.69 | 36 41 26.47| |19 |TC-4 TC-5 TC-8 | 29 15 1.87| 3.01 | 29 15 4.88| |20 |TC-7 TC-6 TC-3 | 54 43 43.68| .93 | 54 43 44.61| -.42 | 44 19 45.03| |21 |TC-3 TC-6 TC-1 | 44 19 45.45| |22 |TC-1 TC-6 TC-5 | 72 25 47.20| -.24 | 72 25 46.96| |23 |TC-3 TC-7 TC-1 | 24 19 57.31| 1.27 | 24 19 58.58| |24 |TC-1 TC-7 TC-6 | 24 52 13.76| -.04 | 24 52 13.72| |25 |TC-5 TC-8 TC-4 | 101 58 24.96| 2.55 | 101 58 27.51| =====================================================================

Cao B¸ H¹

-36 -

Líp Tr¾c ®ÞaB-K48

KÕt qu¶ thu ®îc trong qu¸ tr×nh tÝnh to¸n xö lý:

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

B.TRI DO CANH SAU BINH SAI

=========================================================== | SO | TEN-CANH | CHIEU DAI | HIEU | CHIEU DAI | | THU|----------------| DO | CHINH | SAU BINH SAI | | (m) | (m) | | TU | DAU-CUOI | (m) |----|----------------|------------|-------|--------------| | 1 |TC-3 TC-1 | 630.589 | .000 | 630.589 | | 2 |TC-1 TC-3 | 552.190 | .014 | 552.204 | | 3 |TC-1 TC-4 | 654.023 | -.002 | 654.021 | | 4 |TC-1 TC-5 | 740.025 | -.009 | 740.016 | | 5 |TC-1 TC-6 | 583.878 | .000 | 583.878 | | 6 |TC-1 TC-7 | 1370.990 | .002 | 1370.992 | | 7 |TC-3 TC-3 | 522.073 | -.001 | 522.072 | | 8 |TC-3 TC-7 | 968.974 | -.002 | 968.972 | | 9 |TC-5 TC-4 | 854.348 | -.005 | 854.343 | |10 |TC-5 TC-6 | 663.880 | .003 | 663.883 | |11 |TC-8 TC-4 | 426.757 | -.003 | 426.754 | |12 |TC-8 TC-5 | 656.858 | .003 | 656.861 | ===========================================================

V.KET QUA TOA DO DIEM SAU BINH SAI ====================================

=====================================================================

| S | TEN | TOA DO | SAI SO VI TRI DIEM | | T | |-------------------------------|---------------------- | | T | DIEM | X(m) | Y(m) | Mx(cm)| My(cm)| Md(cm)| |---|-------|---------------|---------------|-------|-------|-------| | 1 |TC-3 | 1430267.793| 277344.173| .36 | .33 | .49 | | 2 |TC-6 | 1429502.226| 276873.888| .32 | .34 | .47 | | 3 |TC-8 | 1428889.977| 277877.689| .49 | .38 | .61 | | 4 |TC-4 | 1429299.989| 277996.048| .35 | .33 | .48 | | 5 |TC-7 | 1430561.261| 276420.711| .72 | .70 | 1.00 | | 6 |TC-3 | 1430047.653| 277817.563| .25 | .16 | .30 | | 7 |TC-1 | 1429644.552| 277440.153| .16 | .13 | .21 | | 8 |TC-5 | 1428937.257| 277222.531| .27 | .14 | .31 | =====================================================================

1. Sai so trung phuong trong so don vi mo = .96 "

Qua vÝ dô trªn, nh×n vµo b¶ng kÕt qu¶ täa ®é b×nh sai trong hai trêng

hîp chóng ta cã thÓ nhËn thÊy:

- KÕt qu¶ b×nh sai kh«ng chÞu ¶nh hëng cña sai sè sè liÖu gèc.

- Víi trêng hîp x¸c ®Þnh ®îc ma trËn ®Þnh vÞ C lµ kh¸c nhau th× kÕt

qu¶ vector trÞ b×nh sai gãc, c¹nh lµ kh«ng ®æi.

- Vector nghiÖm X, ®Æc trng cho sù thay ®æi to¹ ®é hay lµ ®é lÖch to¹

®é cña c¸c ®iÓm, phô thuéc vµo c¸ch lùa chän ma trËn ®Þnh vÞ C.

Tãm l¹i: T¬ng quan néi t¹i gi÷a c¸c yÕu tè trong líi sau b×nh sai còng

nh c¸c ®Æc trng ®é chÝnh x¸c cña líi chØ phô thuéc duy nhÊt vµo vector trÞ

Cao B¸ H¹

-37 -

Líp Tr¾c ®ÞaB-K48

®o.

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

2.4. nhËn xÐt vÒ b×nh sai líi tù do

Xem xÐt m« h×nh vµ quy tr×nh b×nh sai líi tù do cho phÐp chóng t«i rót

ra c¸c nhËn xÐt sau:

1. B×nh sai líi tù do thùc chÊt lµ bµi to¸n b×nh sai gi¸n tiÕp kÌm ®iÒu kiÖn.

Trong qu¸ tr×nh tÝnh to¸n b×nh sai bæ sung hÖ ®iÒu kiÖn rµng buéc vector Èn sè

nh»m gi¶i quyÕt hai nhiÖm vô: Khö tÝnh suy biÕn cña ma trËn ph¬ng tr×nh

chuÈn, x¸c ®Þnh vector nghiÖm duy nhÊt vµ ®Þnh vÞ líi

2. C¸c tÝnh chÊt cña ph¬ng ph¸p b×nh sai líi tù do cho thÊy r»ng bµi to¸n xö

lý líi tr¾c ®Þa tù do cã tÝnh ®Æc thï cao vµ cã nh÷ng ®Æc ®iÓm kh¸c biÖt víi

c¸c bµi to¸n b×nh sai th«ng thêng.

3. ViÖc lùa chän ma trËn ®Þnh vÞ cã ý nghÜa rÊt quan träng trong kÕt qu¶ tÝnh

to¸n b×nh sai, do ®ã ma trËn C cÇn ph¶i ®îc lùa chän mét c¸ch thÝch hîp, phï

hîp víi ®Æc ®iÓm vµ b¶n chÊt cña tõng lo¹i líi.

4. VÊn ®Ò ®Þnh vÞ líi cã liªn quan mËt thiÕt ®Õn bµi to¸n chuyÓn ®æi täa ®é

Helmert, v× vËy vÊn ®Ò ®Þnh vÞ c¸c m¹ng líi tr¾c ®Þa cã b¶n chÊt lµ líi tù do

Cao B¸ H¹

-38 -

Líp Tr¾c ®ÞaB-K48

cÇn ph¶i xem xÐt trªn c¬ së cña phÐp chuyÓn ®æi täa ®é Helmert.

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

Ch¬ng 3

øng dông ph¬ng ph¸p b×nh sai líi tr¾c ®Þa tù do ®Ó xö lý líi thi c«ng c«ng tr×nh

3.1. thuËt to¸n xö lý sè liÖu líi thi c«ng

Líi thi c«ng ®îc thµnh lËp trong giai ®o¹n x©y dùng c«ng tr×nh víi môc

®Ých bè trÝ tæng thÓ, bè trÝ chi tiÕt vµ ®o vÏ hoµn c«ng c«ng tr×nh, líi thi c«ng

gåm nhiÒu bËc líi, ®îc thµnh lËp phô thuéc vµo tiÕn tr×nh thi c«ng c«ng

tr×nh vµ yªu cÇu ®é chÝnh x¸c ®èi víi mçi bËc líi lµ t¨ng dÇn (líi bËc sau cã

®é chÝnh x¸c cao h¬n líi bËc tríc), v× vËy viÖc x©y dùng vµ xö lý líi thi

c«ng ph¶i m·n yªu cÇu sau:

- C¸c bËc líi ph¶i ®îc thµnh lËp trong cïng mét hÖ to¹ ®é (®é cao)

thèng nhÊt.

- Ph¶i lùa chän ph¬ng ph¸p b×nh sai sao cho kÕt qu¶ b×nh sai kh«ng chÞu

¶nh hëng cña sai sè sè liÖu gèc.

Líi thi c«ng c«ng tr×nh thêng ®îc thµnh lËp b»ng c¸c ph¬ng ph¸p nh

ph¬ng ph¸p tam gi¸c, ®a gi¸c hay giao héi…. Ngoµi ra, hiÖn nay líi thi

c«ng c«ng tr×nh cßn cã thÓ ®îc thµnh lËp b»ng c«ng nghÖ GPS.

Ph©n tÝch kh¶ n¨ng øng dông c¸c ph¬ng ¸n b×nh sai ®Ó xö lý c¸c m¹ng

líi thi c«ng, cã mét sè ph¬ng ph¸p b×nh sai th«ng dông sau: ph¬ng ph¸p

b×nh sai líi phô thuéc, ph¬ng ph¸p b×nh sai líi tù do.

Ph¬ng ph¸p b×nh sai líi phô thuéc: Ph¬ng ph¸p b×nh sai nµy sÏ dÉn

®Õn ¶nh hëng sai sè sè liÖu gèc trong kÕt qu¶ xö lý, nh÷ng ®iÓm cµng xa

®iÓm gèc cã sai sè cµng lín (sai sè tÝch luü) vµ nh vËy sÏ g©y ra sù biÕn d¹ng

cña tõng bËc líi.

Ph¬ng ph¸p b×nh sai líi tù do: Ph¬ng ph¸p b×nh sai líi tù do phï hîp

®èi víi viÖc xö lý líi thi c«ng: kÕt qu¶ b×nh sai kh«ng chÞu ¶nh hëng cña sai

Cao B¸ H¹

-39 -

Líp Tr¾c ®ÞaB-K48

sè sè liÖu gèc, qu¸ tr×nh ®Þnh vÞ líi linh ho¹t.

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

Nh vËy viÖc xö lý líi thi c«ng c«ng tr×nh sÏ ®îc chóng t«i thùc hiÖn

trªn c¬ së bµi to¸n tr¾c ®Þa tù do (thùc hiÖn cho c¶ líi mÆt b»ng vµ ®é cao).

3.1.1. Xö lý líi mÆt b»ng thi c«ng

3.1.1.1. ThuËt to¸n

Trªn c¬ së bµi to¸n b×nh sai líi tr¾c ®Þa tù do ®· nãi ë ch¬ng 2, trong

ch¬ng nµy chóng t«i vËn dông nªu lªn quy tr×nh gi¶i quyÕt bµi to¸n xö lý sè

liÖu líi mÆt b»ng thi c«ng, c¸c bíc b×nh sai vµ tÝnh to¸n ®îc thùc hiÖn

theo tr×nh tù sau:

a. Èn sè

Èn sè ®îc chän lµ täa ®é b×nh sai cña tÊt c¶ c¸c ®iÓm trong líi.

b. Chän trÞ gÇn ®óng

TrÞ gÇn ®óng lµ to¹ ®é cña c¸c ®iÓm ®· cã trong khu vùc x©y dùng (bao gåm

c¸c ®iÓm nhµ níc cã trong khu vùc, c¸c ®iÓm cßn l¹i sau giai ®o¹n kh¶o s¸t

thiÕt kÕ cã thÓ sö dông ®îc)

c. HÖ ph¬ng tr×nh sè hiÖu chØnh

Ph¬ng tr×nh sè hiÖu chØnh cã d¹ng tæng qu¸t nh sau:

V = AX + L (3. 1)

trong ®ã: A - Ma trËn hÖ sè hÖ ph¬ng tr×nh sè hiÖu chØnh

X - Vector Èn sè

V, L - Vector sè hiÖu chØnh vµ vector sè h¹ng tù do

§èi víi mçi lo¹i trÞ ®o c¸c hÖ sè cña ph¬ng tr×nh sè hiÖu chØnh ®îc tÝnh nh

1. Ph¬ng tr×nh sè hiÖu chØnh gãc (h×nh 3. 1) j

 i

Cao B¸ H¹

-40 -

Líp Tr¾c ®ÞaB-K48

H×nh 3.1. Gãc ®o

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp













(3. 2)

 a

 x 

 y 

xa  ij

yb  ij

xa  ik

yb  . ik

 b ik

b ij



)



sin(



cos(





b ij

)







trong ®ã: ;

b ik

sin( S

cos( S















do

;

2. Ph¬ng tr×nh sè hiÖu chØnh cho c¹nh (h×nh 3. 2)

k Sik







H×nh 3.2. C¹nh ®o

V ik

xa  ik

yb  ik

dxa ik

dyb ik

(3. 3)









Sin



trong ®ã:

 

ik Cos 

ik

b ik

ik



do

; ;

3. Ph¬ng tr×nh sè hiÖu chØnh ph¬ng vÞ (h×nh 3. 3)

ik







H×nh 3.3. Gãc ph¬ng vÞ ®o

xb  ik

ya  ik

xb  ik

ya  ik

V 

l 

(3. 4)

 0 





aik, bik ®îc x¸c ®Þnh theo c«ng thøc trong ph¬ng tr×nh (3. 2)

d. HÖ ph¬ng tr×nh chuÈn

Cao B¸ H¹

-41 -

Líp Tr¾c ®ÞaB-K48

(3. 5) RX + b = 0

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

R = ATPA ; b = ATPL Víi :

e. X¸c ®Þnh ®iÒu kiÖn ®Þnh vÞ líi theo vÞ trÝ ®iÓm

Ma trËn R trong (3. 5) suy biÕn nªn cÇn x¸c lËp hÖ ®iÒu kiÖn rµng buéc

®èi víi vector Èn sè X díi d¹ng:

CTX= 0 (3. 6)

(3. 6) tháa m·n ®iÒu kiÖn:

- Sè lîng cét trong ma trËn C ph¶i b»ng sè khuyÕt (d) trong líi.

- C¸c phÇn tö trong ma trËn C ®îc x¸c ®Þnh theo c«ng thøc sau:

' y i x

' x i y



' i

01   10 

  

- víi i lµ ®iÓm ®Þnh vÞ (3. 7) ci =

0000 0000

  

  

- víi i lµ c¸c ®iÓm kh¸c ci =

f. Gi¶i hÖ ph¬ng tr×nh chuÈn më réng

HÖ ph¬ng tr×nh chuÈn më réng cã d¹ng

CR T

  C 

  

  

  

b   

  

(3. 8)

HÖ ph¬ng tr×nh chuÈn më réng (3. 8) ®îc gi¶i khi x¸c ®Þnh ®îc c¸c

TC T



~ RRE

biÓu thøc tÝnh ma trËn R~ vµ T.

Gi¶ sö tån t¹i ma trËn víi tÝnh chÊt RB = 0, nh©n 2 vÕ biÓu thøc trªn Trong [4] ®· x¸c ®Þnh ®îc dkB  

TC T



víi ma trËn B ta ®îc

RBRBB    1 BCBT

VËy (3. 9)

1 





Ma trËn gi¶ nghÞch ®¶o ®îc x¸c ®Þnh theo c«ng thøc tÝnh sau [1], [4]:

 R

  

CCP 0

TTP 0



BCBT (



(3. 10)

víi

1 





Khi P0 = E

 R

  

(3. 11)

Cao B¸ H¹

-42 -

Líp Tr¾c ®ÞaB-K48

Tõ c«ng thøc (3. 10), chän ma trËn P0 (kÝch thíc dd) lµ ma trËn ®êng chÐo

§å ¸n tèt nghiÖp

Khoa Tr¾c ®Þa



d¹ng

P 0

dd 

10      

1 

CPC







(3. 12)

XÐt

 R



 R



T

       TTP 0

lim m 

 0 

 TTP lim 0



Khi m  th×



TCCP





Nh vËy víi m ®ñ lín th× chóng ta cã thÓ viÕt l¹i ®¼ng thøc (3.10) nh sau:

 R

 1

(3.13)

Thùc nghiÖm cho thÊy c«ng thøc (3.13) cã ®ñ ®é chÝnh x¸c khi chän m  6.

Sau khi tÝnh ®îc ma trËn gi¶ nghÞch ®¶o R~

Vector nghiÖm ®îc tÝnh theo c«ng thøc:

(3. 14)

hay X = - ( R+CP0CT)-1.b ; X = - R~.b

Vector täa ®é b×nh sai ®îc tÝnh theo c«ng thøc

(3. 15) Xbs = X(0) +X

X(0) lµ täa ®é vector gÇn ®óng.

g. §¸nh gi¸ ®é chÝnh x¸c c¸c yÕu tè trong líi



- Sai sè trung ph¬ng ®¬n vÞ träng sè

V T PV kn 

(3. 16)

 trong ®ã - Sai sè vÞ trÝ ®iÓm



: lµ lîng trÞ ®o thõa trong líi.

2 mm  x

2 y



(3. 17)

~ YY

~ XX

;



- Sai sè trung ph¬ng cña hµm Èn sè

1 P F

Cao B¸ H¹

-43 -

Líp Tr¾c ®ÞaB-K48

(3. 18)

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

~ fRf

T

1 FP

f - vector hÖ sè khai triÓn cña hµm sè.

Träng sè ®¶o cña hµm sè ®îc tÝnh theo c«ng thøc:

3.1.1.2. s¬ ®å khèi vµ quy tr×nh xö lý líi mÆt b»ng thi c«ng

S¬ ®å khèi vµ quy tr×nh b×nh sai líi mÆt b»ng thi c«ng c«ng tr×nh ®îc

B¾t ®Çu

§äc file sè liÖu

LËp hÖ ph¬ng tr×nh sè hiÖu chØnh

LËp hÖ ph¬ng tr×nh chuÈn thêng

Chän ®iÒu kiÖn ®Þnh vÞ: CTX= 0

CR T

Gi¶i hÖ ph¬ng tr×nh chuÈn më réng x    k 

  

  

  

  C 

b   

B×nh sai vµ ®¸nh gi¸ ®é chÝnh x¸c

In kÕt qu¶

KÕt thóc

chóng t«i cô thÓ ho¸ nh h×nh 3.4.

Cao B¸ H¹

-44 -

Líp Tr¾c ®ÞaB-K48

H×nh 3. 4. S¬ ®å khèi ch¬ng tr×nh b×nh sai líi mÆt b»ng thi c«ng c«ng tr×nh.

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

3.1.1.3. cÊu tróc ch¬ng tr×nh b×nh sai

Sù ph¸t triÓn vµ øng dông ngµy cµng réng r·i cña c«ng nghÖ th«ng tin

cho phÐp ¸p dông c¸c ph¬ng ph¸p chÆt chÏ vµo viÖc xö lý sè liÖu líi tr¾c ®Þa

c«ng tr×nh. V× vËy viÖc nghiªn cøu lËp ch¬ng tr×nh tÝnh to¸n trªn m¸y tÝnh lµ

cÇn thiÕt vµ rÊt cã ý nghÜa ®èi víi viÖc häc tËp còng nh øng dông trong s¶n

xuÊt. Tríc hÕt chóng ta bµn vÒ thuËt to¸n lµm c¬ së cho viÖc lËp tr×nh (thuËt

to¸n ®îc x©y dùng theo néi dung cña bµi to¸n b×nh sai líi tr¾c ®Þa tù do ®·

nãi ë ch¬ng 2). Sau ®©y sÏ giíi thiÖu cÊu tróc ch¬ng tr×nh b×nh sai líi mÆt

b»ng.

1. CÊu tróc ch¬ng tr×nh chÝnh

Dùa vµo thuËt to¸n vµ quy tr×nh ®· ®îc x©y dùng nh trªn, ch¬ng tr×nh

xö lý líi mÆt b»ng thi c«ng ®îc lËp cã cÊu tróc nh sau:

a. LËp ph¬ng tr×nh sè hiÖu chØnh

Dùa vµo cÊu tróc file d÷ liÖu vµ c¸ch m· hãa líi (tr×nh bµy phÇn sau) sÏ

thµnh lËp ®îc ph¬ng tr×nh sè hiÖu chØnh gãc (3. 2) vµ ph¬ng tr×nh sè hiÖu

chØnh c¹nh (3. 3). C¸c hÖ sè cña mçi ph¬ng tr×nh sè hiÖu chØnh ®îc lu gi÷

trong vector A cã ®é dµi 2*k phÇn tö (k lµ sè ®iÓm trong líi), mçi khi mét

ph¬ng tr×nh sè hiÖu chØnh ®îc thµnh lËp th× sÏ tham gia ngay vµo lËp

ph¬ng tr×nh chuÈn.

b. LËp hÖ ph¬ng tr×nh chuÈn

Ma trËn R, vector sè h¹ng tù do ®îc chuyÓn sang m¶ng mét chiÒu vµ

R i

(3. 19)



1  

b i

 b i

T  i Pla i

1 

trong ®ã Ri, bi lµ ma trËn hÖ sè vµ vector sè h¹ng tù do tÝnh ®Õn trÞ ®o thø i-1

®îc tÝnh theo c«ng thøc truy håi:

Cao B¸ H¹

-45 -

Líp Tr¾c ®ÞaB-K48

ai, p - vector trÞ ®o vµ träng sè vector thø i

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

C¸c gi¸ trÞ khëi ®Çu Ro = 0; bo = 0;

C¸c hÖ sè cña hÖ ph¬ng tr×nh chuÈn ®îc lu gi÷ trong vector R, b¾t

®Çu tõ phÇn tö 1 m t¬ng øng víi ®Þa chØ cña chóng trong b¶ng sau:

1 2 4 7 ....

3 5 8 m

6 9 ....

(





10 ....

j  2

(3. 20)

Víi i, j - lµ chØ sè thø tù hµng vµ cét trªn m¶ng 2 chiÒu

m - ®Þa chØ cña phÇn tö ®ã trong m¶ng mét chiÒu.

c. LËp ma trËn ®Þnh vÞ

Líi mÆt b»ng thi c«ng c«ng tr×nh ®o gãc c¹nh nªn cã sè khuyÕt d=3,

d¹ng (x, y, α) nªn C ®îc viÕt díi d¹ng:

01   

y '   x  ' 

000

- víi i lµ ®iÓm ®Þnh vÞ ci=

000

  

  

- víi i lµ c¸c ®iÓm kh¸c ci=

d. TÝnh ma trËn gi¶ nghÞch ®¶o vµ ®¸nh gi¸ ®é chÝnh x¸c

- Ma trËn gi¶ nghÞch ®¶o ®îc tÝnh theo c«ng thøc (3.13), víi P0 ®îc

viÕt nh (3.12). Trong ®å ¸n nµy chóng t«i chän m=7

- §é chÝnh x¸c ®îc x¸c ®Þnh theo c¸c c«ng thøc (3.16), (3.17), (3.18).

§Ó lµm râ h¬n vÒ tÝnh æn ®Þnh cña c¸c ®iÓm líi ta tiÕn hµnh ®¸nh gi¸ sai

sè vÞ trÝ ®iÓm theo chuÈn elip sai sè.

§Æc trng x¸c ®Þnh elip sai sè lµ b¸n trôc lín E, b¸n trôc nhá F vµ gãc

Cao B¸ H¹

-46 -

Líp Tr¾c ®ÞaB-K48

®Þnh híng E. Theo [1], [7], [10] ta x¸c ®Þnh ®îc c¸c th«ng sè trªn nh sau:

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

(

)

Q (

)

Q 4









2 xy

(

)

Q (

)

Q 4









(3.21)

 

 2

2 m 0 2 2 m 0 2

2 Q

xy Q



(3.22) tg2E =

víi QXX, QYY, QXY lµ träng sè ®¶o cña to¹ ®é X(Qxx), to¹ ®é Y(Qyy) vµ träng sè ®¶o t¬ng quan (Qxy) cña tõng ®iÓm cÇn ®¸nh gi¸.

C¸c träng sè ®¶o nµy ®îc x¸c ®Þnh th«ng qua ph¬ng ph¸p b×nh sai gi¸n

tiÕp nh ®· tr×nh bµy ë phÇn trªn. Dùa vµo c«ng thøc ë trªn, ta tÝnh ®îc b¸n

trôc lín E, b¸n trôc nhá F, gãc ®Þnh híng cña b¸n trôc lín E, tõ ®ã x©y dùng

®îc elip sai sè.

2. CÊu tróc d÷ liÖu cña ch¬ng tr×nh

§Ó phï hîp víi ch¬ng tr×nh chÝnh, chóng t«i ®· tæ chøc tÖp d÷ liÖu cho

ch¬ng tr×nh víi cÊu tróc nh sau:

a. X¸c ®Þnh c¸c tham sè kü thuËt cña líi

- Tªn c«ng tr×nh.

- Sè lîng ®iÓm tham gia ®Þnh vÞ, sè lîng ®iÓm kh¸c, sè lîng c¹nh ®o,

sè lîng gãc ®o, sè lîng ph¬ng vÞ ®o.

- C¸c ®Æc trng vÒ ®é chÝnh x¸c.

b. M· hãa th«ng tin líi

- C¸c ®iÓm cña líi ®îc ®¸nh sè liªn tôc tõ 1 ®Õn hÕt theo nguyªn t¾c: c¸c ®iÓm cña líi bËc sau ®îc ®¸nh sè tríc, sau ®ã ®Õn c¸c ®iÓm cña líi c¬ së.

- Tªn c¸c ®iÓm cña líi ®îc lu gi÷ trong m¶ng riªng còng theo nguyªn

t¾c trªn.

- Gi¸ trÞ to¹ ®é gÇn ®óng ®îc lu trong mét m¶ng kh¸c theo thø tù t¨ng

Cao B¸ H¹

-47 -

Líp Tr¾c ®ÞaB-K48

dÇn cña m· sè c¸c ®iÓm líi.

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

- C¸c gãc ®o ®îc m· hãa theo nguyªn t¾c: M· sè cña ®iÓm tr¸i, m· sè

cña ®iÓm gi÷a, m· sè cña ®iÓm ph¶i, gi¸ trÞ gãc ®o (®é, phót, gi©y)

- C¸c c¹nh ®o ®îc m· ho¸ theo nguyªn t¾c: m· sè cña ®iÓm §Çu, m· sè

cña ®iÓm Cuèi, gi¸ trÞ c¹nh ®o (chiÒu dµi c¹nh ®o).

- c¸c ph¬ng vÞ ®o ®îc m· ho¸ theo nguyªn t¾c: M· sè cña ®iÓm ®Çu,

m· sè cña ®iÓm cuèi, gi¸ trÞ ph¬ng vÞ ®o (®é, phót, gi©y)

3.1.2. Xö lý líi ®é cao thi c«ng

Còng nh líi mÆt b»ng, líi ®é cao thi c«ng ®îc xö lý theo thuËt to¸n

vµ quy tr×nh t¬ng tù nh sau:

3.1.2.1. ThuËt to¸n

a. Chän Èn sè vµ ®é cao gÇn ®óng

- Èn sè ®îc chän lµ ®é cao b×nh sai cña tÊt c¶ c¸c ®iÓm trong líi.

- §é cao gÇn ®óng lµ ®é cao cña c¸c ®iÓm ®· cã trªn khu vùc thi c«ng

c«ng tr×nh (®é cao c¸c ®iÓm nhµ níc cã trong khu vùc x©y dùng, c¸c ®iÓm ®é

cao cã trong c¸c giai ®o¹n x©y dùng tríc ®ã mµ cã thÓ sö dông ®îc)

b. LËp ph¬ng tr×nh sè hiÖu chØnh cña c¸c trÞ ®o

Ph¬ng tr×nh sè hiÖu chØnh cña trÞ ®o thø m trong líi gi÷a hai ®iÓm i vµ k









(h×nh 3.5) ®îc biÔu diÔn díi d¹ng tuyÕn tÝnh:

lH  i

, (3.23)

hm i k

H×nh 3.5 S¬ ®å tuyÕn thuû chuÈn

(

)





Trong ®ã, nh ®· biÕt:

0 k

0 i

lµ sè h¹ng tù do.

kH

iH

mp lµ träng sè cña chªnh cao mh t¬ng øng.

Cao B¸ H¹

-48 -

Líp Tr¾c ®ÞaB-K48

vµ lµ sè hiÖu chØnh vµo ®é cao gÇn ®óng cña ®iÓm k vµ i.

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

mja C¸c hÖ sè theo nguyªn t¾c sau:

cña ph¬ng tr×nh sè hiÖu chØnh trÞ ®o m ®îc x¸c ®Þnh

-1, nÕu j=i;

mja

1, nÕu j=k;

0, nÕu j kh¸c i vµ k.

HÖ ph¬ng tr×nh sè hiÖu chØnh viÕt díi d¹ng ma trËn:

V = AX + L

c. Thµnh lËp hÖ ph¬ng tr×nh chuÈn

0 b

HÖ ph¬ng tr×nh chuÈn Èn sè viÕt díi d¹ng ma trËn:

(3.24)

T PAAR



T aap i



1 

T PLA



Trong ®ã:

T lap i i

n  1 i 

......

)

( 



NÕu P lµ ma trËn ®êng chÐo th× c¸c phÇn tö cña ma trËn hÖ sè hÖ ph¬ng tr×nh chuÈn R sÏ ®îc x¸c ®Þnh kh¸ ®¬n gi¶n theo nguyªn t¾c do V. V. Popov ®Ò xuÊt:



- §èi víi c¸c phÇn tö trªn ®êng chÐo:

 i j 

(3.25)

nghÜa lµ b»ng tæng träng sè cña c¸c tuyÕn xuÊt ph¸t t¹i ®iÓm j.



- §èi víi c¸c phÇn tö ngoµi ®êng chÐo:

 i jt 

(3.26)

nghÜa lµ b»ng tæng träng sè cña c¸c tuyÕn n»m gi÷a 2 ®iÓm j vµ t.

NÕu c¸c ®iÓm j vµ t nãi ë trªn lµ nh÷ng ®iÓm nót th× ®©y chÝnh lµ néi

dung cña ph¬ng ph¸p ®iÓm nót.





- §èi víi c¸c sè h¹ng tù do:

lp i

 i j 

Cao B¸ H¹

-49 -

Líp Tr¾c ®ÞaB-K48

(3.27)

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

d. Chän ®iÒu kiÖn ®Þnh vÞ

Nh ®· biÕt, hÖ ph¬ng tr×nh ®iÒu kiÖn ®Þnh vÞ trong b×nh sai líi tù do

cã d¹ng tæng qu¸t:

CTX = 0 (3.28)

§èi víi líi ®é cao tù do, sè khuyÕt d=1, do vËy C lµ vector gåm n phÇn

tö (n lµ tæng sè ®iÓm trong líi). C¸c phÇn tö nµy ®îc lùa chän nh sau:

ci = 1 øng víi c¸c ®iÓm ®é cao c¬ së æn ®Þnh.

ci = 0 øng víi c¸c ®iÓm kh¸c.

e. LËp vµ gi¶i hÖ ph¬ng tr×nh chuÈn më réng

X K

b 0

  

  

  

  

1

   Sau khi tÝnh ma trËn gi¶ nghÞch ®¶o: T R TT

)

(







HÖ ph¬ng tr×nh chuÈn më réng cã d¹ng :

~

1) 

(

sÏ t×m ®îc nghiÖm theo c«ng thøc: bR (3.29)



]. b

[(

)

Còng cã thÓ t×m nghiÖm theo c«ng thøc:  (3.30)

1  



(

1)





ThËt vËy, tõ (3. 33) cã thÓ viÕt l¹i nh sau: 

1

Hay: (3.31)

T PLA

(

)

( BCABT

[

)

]



NhËn thÊy r»ng: T T b = 0 (Do AB = 0)



(

TCC

1) 





V× vËy hoµn toµn cã thÓ tÝnh nghiÖm theo (3. 30).



 RRR

 R

Tuy nhiªn, cÇn lu ý r»ng ma trËn kh«ng cã tÝnh chÊt

, v× thÕ kh«ng dïng nã nh lµ ma trËn träng sè ®¶o ®Ó ®¸nh gi¸

®é chÝnh x¸c ®îc.

f. TÝnh T vµ TTT

Cao B¸ H¹

-50 -

Líp Tr¾c ®ÞaB-K48

§Ó tÝnh nghiÖm vµ ®¸nh gi¸ ®é chÝnh x¸c theo ma trËn gi¶ nghÞch ®¶o,

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

BCBT (



BC T (

)

cÇn ph¶i x¸c ®Þnh thªm ma trËn T. Nh ®· biÕt: 1) 

§èi víi líi ®é cao tù do, lµ ma trËn mét phÇn tö, v× vËy dÔ dµng



chøng minh r»ng:

1 k

(3. 32)



Tõ ®ã tÝnh ®îc:

1 2

(3. 33)

víi k lµ sè ®iÓm tham gia ®Þnh vÞ.

g. B×nh sai

Sau khi t×m ®îc nghiÖm cña hÖ ph¬ng tr×nh chuÈn më réng, sÏ tiÕn

hµnh tÝnh:

 0 hh



- Vector chªnh cao b×nh sai:

(3. 34)

HH 



- Vector ®é cao b×nh sai:

(3. 35)

víi h0 vµ H0 lµ vector trÞ ®o vµ vector ®é cao gÇn ®óng.

h. TÝnh ma trËn gi¶ nghÞch ®¶o vµ ®¸nh gi¸ ®é chÝnh x¸c

1

(

)







1- TÝnh ma trËn gi¶ nghÞch ®¶o:

(3.36)

Cã thÓ sö dông ph¬ng ph¸p Gauss (cét phô) hoÆc ph¬ng ph¸p Ganzen ®Ó

tÝnh ma trËn (R + CCT)-1. Sau ®ã trõ ®i ma trËn TTT.

2- §¸nh gi¸ ®é chÝnh x¸c:

- Sai sè trung ph¬ng träng sè ®¬n vÞ:

0

V T PV dtn 

(3.37)



- Sai sè trung ph¬ng cña c¸c Èn sè:

~ XX

Cao B¸ H¹

-51 -

Líp Tr¾c ®ÞaB-K48

(3.38)

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

fRf

- Sai sè trung ph¬ng cña hµm c¸c Èn sè:

0

(3.39)

Trong ®ã: n lµ sè lîng trÞ ®o, t lµ sè lîng Èn sè, d lµ sè khuyÕt cña líi, vµ f

lµ vector hÖ sè cña hµm cÇn ®¸nh gi¸.

B¾t ®Çu

§äc file sè liÖu

LËp hÖ ph¬ng tr×nh sè hiÖu chØnh: V= AX+ L

LËp hÖ ph¬ng tr×nh chuÈn thêng: RX+ b= 0

Chän ®iÒu kiÖn ®Þnh vÞ: CTX= 0 (§Þnh vÞ vµo tÊt c¶ c¸c ®iÓm cña líi c¬ së)

X K

b 0

LËp vµ gi¶i hÖ ph¬ng tr×nh chuÈn më réng:   

  

  

  

  

B×nh sai vµ ®¸nh gi¸ ®é chÝnh x¸c

In kÕt qu¶

KÕt thóc

3.1.2.2. s¬ ®å khèi vµ quy tr×nh xö lý líi ®é cao thi c«ng

Cao B¸ H¹

-52 -

Líp Tr¾c ®ÞaB-K48

H×nh 3. 6. S¬ ®å khèi ch¬ng tr×nh b×nh sai líi ®é cao thi c«ng c«ng tr×nh.

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

3.1.2.3. cÊu tróc ch¬ng tr×nh b×nh sai

1. CÊu tróc ch¬ng tr×nh chÝnh

líi ®é cao thi c«ng cña chóng t«i ®îc lËp cã cÊu tróc nh sau:

a. Thµnh lËp hÖ ph¬ng tr×nh sè hiÖu chØnh

Ph¬ng tr×nh sè hiÖu chØnh cña c¸c chªnh cao ®o ®îc biÓu diÔn díi









d¹ng tuyÕn tÝnh nh c«ng thøc (3. 23):

lH  i

C¸c gi¸ trÞ hÖ sè cña mçi mét ph¬ng tr×nh sè hiÖu chØnh d¹ng nµy ®îc

lu gi÷ trong vector HV(n) cã ®é dµi 3 phÇn tö, trong ®ã hai phÇn tö ®Çu dµnh

chøa hÖ sè ph¬ng tr×nh sè hiÖu chØnh, vµ phÇn tö thø ba chøa sè h¹ng tù do.

Vector nµy dïng chung cho tÊt c¶ c¸c trÞ ®o, nghÜa lµ mçi mét ph¬ng

tr×nh sè hiÖu chØnh sau khi tham gia lËp ph¬ng tr×nh chuÈn sÏ nhêng chç ®Ó

chøa c¸c hÖ sè cña ph¬ng tr×nh sè hiÖu chØnh kh¸c. C¸c hÖ sè ®îc s¾p xÕp

theo thø tù Sau-Tríc (chiÒu cña tuyÕn ®o) vµ ®îc m« t¶ nh h×nh 3. 7.

mia

mka

HV(n)

H×nh 3. 7. HÖ sè hÖ ph¬ng tr×nh sè hiÖu chØnh

b. Thµnh lËp hÖ ph¬ng tr×nh chuÈn

C¸c hÖ sè cña hÖ ph¬ng tr×nh chuÈn ®îc lu gi÷ trong vector Ptc(N),

b¾t ®Çu tõ phÇn tö 1 ®Õn phÇn tö N t¬ng øng víi ®Þa chØ cña chóng trªn b¶ng

hÖ sè hÖ ph¬ng tr×nh chuÈn nh sau:

1 2 4 7 ....

3 5 8 ....

6 9 ....

10 ....

C¸c ®Þa chØ nµy ®îc x¸c ®Þnh theo c«ng thøc chuyÓn ®æi tõ m¶ng hai

Cao B¸ H¹

-53 -

Líp Tr¾c ®ÞaB-K48

chiÒu sang m¶ng mét chiÒu tÝnh theo (3. 40):

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

2/)1

i 

i 

j ( 

nÕu

2/)1

i 

j 

ii ( 

(3. 40) nÕu

Trong ®ã:

- i vµ j t¬ng øng lµ chØ sè hµng vµ cét cña phÇn tö trªn m¶ng hai chiÒu.

- k lµ ®Þa chØ cña phÇn tö ®ã trªn m¶ng mét chiÒu.

TrËt tù s¾p xÕp c¸c hÖ sè cña hÖ ph¬ng tr×nh chuÈn vµo m¶ng (vector) ptc(N)

®îc m« t¶ nh h×nh 3. 8:

... ... ptc(N) R1 R2 R3 RN

H×nh 3. 8. HÖ sè hÖ ph¬ng tr×nh chuÈn

Khi lËp hÖ ph¬ng tr×nh chuÈn, chóng ta sö dông c«ng thøc R = ATPA. C¸c

....





phÇn tö cña ma trËn R cã thÓ viÕt díi d¹ng:

aap 11 1 i

aap 2

aap ni

(3. 41)

nR lµ hÖ sè cña hÖ ph¬ng tr×nh chuÈn tÝnh tõ trÞ ®o thø nhÊt ®Õn

NÕu ký hiÖu



trÞ ®o thø n th× lóc ®ã cã thÓ viÕt:

n ij

aap ki

n  1 k 

(3. 42)

1

apa





Nh vËy, c«ng thøc (3. 42) t¬ng ®¬ng víi c«ng thøc truy håi:

T i

(3. 43)

1nR

Trong ®ã:

nR - Ma trËn hÖ sè cña hÖ ph¬ng tr×nh chuÈn tÝnh ®Õn trÞ ®o thø n.

a - Vector hÖ sè cña ph¬ng tr×nh sè hiÖu chØnh trÞ ®o thø n.

- Ma trËn hÖ sè cña hÖ ph¬ng tr×nh chuÈn tÝnh ®Õn trÞ ®o thø n-1.

t (

2/)1





Sè h¹ng tù do còng ®îc xÕp chung vµo m¶ng ptc(N) theo ®Þa chØ:

(3. 44)

1





víi gi¸ trÞ tÝnh theo c«ng thøc truy håi:

T lpa i i

Cao B¸ H¹

-54 -

Líp Tr¾c ®ÞaB-K48

(3. 45)

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

t )(1

2/)2

tN ( 



§é dµi cña vector ptc(N) ®îc x¸c ®Þnh theo c«ng thøc:

(3. 46)

i' lµ chØ sè cña sè h¹ng tù do cña hÖ ph¬ng tr×nh chuÈn.

c. Chän ®iÒu kiÖn ®Þnh vÞ

Giai ®o¹n ®Çu cña bíc ®Þnh vÞ, chóng t«i chän ®iÒu kiÖn ®Þnh vÞ theo

tiªu chuÈn ®· nãi ë tiÕt 2.3:

ci = 1 øng víi c¸c ®iÓm ®é cao c¬ së.

ci = 0 øng víi c¸c ®iÓm kh¸c.

NÕu s¾p xÕp c¸c ®iÓm ®Þnh vÞ xuèng cuèi danh s¸ch, th× ma trËn ®Þnh vÞ C sÏ

......

)1....1110

000(

cã d¹ng nh sau:

t cét k cét

CÇn lu ý r»ng ®iÒu kiÖn nµy kh«ng ph¶i lµ cè ®Þnh, nã cã thÓ sÏ ®îc

x¸c lËp l¹i nhê qu¸ tr×nh tÝnh lÆp nÕu biÕn so s¸nh cña ch¬ng tr×nh ph¸t hiÖn

thÊy cã ®iÓm ®Þnh vÞ nµo ®ã cña líi c¬ së kh«ng æn ®Þnh.



(

TCC

1) 





d. TÝnh ma trËn gi¶ nghÞch ®¶o

Nh ®· nãi ë tiÕt 3.1, v× ma trËn chØ cã thÓ dïng ®Ó

~R võa

kh«ng tÝnh nghiÖm theo (3. 30), mµ tÝnh lu«n ma trËn gi¶ nghÞch ®¶o

®Ó tÝnh nghiÖm theo (3.29), võa ®Ó ®¸nh gi¸ ®é chÝnh x¸c. Ma trËn gi¶ nghÞch

1

(

)







®¶o ®îc x¸c ®Þnh theo c«ng thøc:

(3.47)

Lu ý r»ng nÕu s¾p xÕp c¸c ®iÓm ®Þnh vÞ xuèng cuèi danh s¸ch cña c¸c

TCC sÏ bao gåm c¸c phÇn tö b»ng 1 kÓ tõ dßng

Cao B¸ H¹

-55 -

Líp Tr¾c ®ÞaB-K48

®iÓm trong líi, th× ma trËn

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

thø (t+1) ®Õn dßng thø (t+k) (víi k lµ sè ®iÓm tham gia ®Þnh vÞ vµ t lµ sè ®iÓm

000

........

cßn l¹i cña líi):

......

..........

......

TCC



111

t dßng

....... 1

         

         

k dßng

Thùc hiÖn phÐp lÊy tæng kh¸ ®¬n gi¶n cña 2 ma trËn cã cïng kÝch thíc,

gi÷ nguyªn ma trËn R víi c¸c hµng tõ 1 ®Õn t vµ céng thªm 1 vµo c¸c gi¸ trÞ Ri víi i cã gi¸ trÞ tõ (t+1) ®Õn (t+k) sÏ t×m ®îc (R + CCT).

Cuèi cïng, ma trËn gi¶ nghÞch ®¶o ®îc x¸c ®Þnh nhê phÐp lÊy hiÖu 2 ma trËn

theo (3. 47), trong ®ã TTT lµ ma trËn cã c¸c phÇn tö b»ng nhau vµ b»ng 1/k2.

C¸c phÇn tö cña ma trËn gi¶ nghÞch ®¶o ®îc lu gi÷ trong m¶ng RLV(N) xÕp

chÌn lªn c¸c phÇn tö cña ma trËn hÖ sè hÖ ph¬ng trinh chuÈn.

Sö dông ma trËn gi¶ nghÞch ®¶o ®Ó tÝnh nghiÖm theo (3.29).

B×nh sai vµ ®¸nh gi¸ ®é chÝnh x¸c ®îc thùc hiÖn theo c¸c c«ng thøc tõ

(3.34) ®Õn (3.39).

2. CÊu tróc d÷ liÖu cña ch¬ng tr×nh

§Ó ch¬ng tr×nh cã thÓ ho¹t ®éng ®îc víi nh÷ng sè liÖu cña líi ®· cho,

chóng t«i ®· tæ chøc tÖp d÷ liÖu cho ch¬ng tr×nh víi cÊu tróc nh sau:

a. X¸c ®Þnh c¸c tham sè kü thuËt cña líi

- Tªn c«ng tr×nh.

- Sè ®iÓm líi bËc sau.

- Sè lîng ®iÓm tham gia ®Þnh vÞ.

- Sè lîng chªnh cao ®o.

Cao B¸ H¹

-56 -

Líp Tr¾c ®ÞaB-K48

- C¸c ®Æc trng vÒ ®é chÝnh x¸c.

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

b. M· ho¸ th«ng tin líi

- C¸c ®iÓm cña líi ®îc ®¸nh sè liªn tôc tõ mét ®Õn hÕt theo nguyªn

t¾c: c¸c ®iÓm cña líi bËc sau ®îc ®¸nh sè tríc, sau ®ã ®Õn c¸c ®iÓm cña

líi c¬ së.

- Tªn c¸c ®iÓm cña líi ®îc lu gi÷ trong m¶ng riªng còng theo nguyªn

t¾c trªn.

- Gi¸ trÞ ®é cao gÇn ®óng ®îc lu trong mét m¶ng kh¸c theo thø tù t¨ng

dÇn cña m· sè c¸c ®iÓm líi.

- C¸c chªnh cao ®o ®îc m· ho¸ theo nguyªn t¾c: m· sè cña ®iÓm Sau,

m· sè cña ®iÓm Tríc, gi¸ trÞ chªnh cao ®o, sè tr¹m ®o (chiÒu dµi c¹nh ®o).

3.2. lËp ch¬ng tr×nh b×nh sai

Sau khi nghiªn cøu bµi to¸n b×nh sai líi tù do, quy tr×nh xö lý vµ c¸c

thuËt to¸n ¸p dông, chóng t«i tiÕn hµnh thµnh lËp ch¬ng tr×nh b×nh sai líi thi

c«ng c«ng tr×nh trªn m¸y tÝnh víi tªn gäi BuildNet. Ch¬ng tr×nh ®îc chóng

t«i viÕt b»ng ng«n ng÷ lËp tr×nh FORTRAN-77, giao diÖn ®îc thiÕt kÕ trªn

nÒn Delphi 6. C¸c bíc ®îc thµnh lËp nh sau:

- ThiÕt kÕ giao diÖn ch¬ng tr×nh

- Tæ chøc, m· hãa file d÷ liÖu.

- C¸c ch¬ng tr×nh nguån.

3.2.1. ThiÕt kÕ giao diÖn ch¬ng tr×nh

Giao diÖn phÇn mÒm BuildNet ®îc thiÕt kÕ theo d¹ng chuÈn cña mét

phÇn mÒm øng dông, cã hiÓn thÞ tiÕng viÖt dÔ sö dông. Giao diÖn chÝnh cña

Cao B¸ H¹

-57 -

Líp Tr¾c ®ÞaB-K48

ch¬ng tr×nh ®îc thÓ hiÖn nh h×nh 3.9.

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

H×nh 3.9. Giao diÖn chÝnh cña ch¬ng tr×nh Buildnet

1. Khëi ®éng BuildNet, vµo thùc ®¬n Binh sai luoi mat bang sau ®ã vµo

Binh sai luoi mat bang tu do sÏ cã giao diÖn modul b×nh sai líi mÆt b»ng tù

do nh h×nh 3.10.

2. Vµo Mo file so lieu më tÖp d÷ liÖu ®· cã, ta chän File sè liÖu ®· so¹n

s½n (H×nh 3.11).

3. Cã thÓ t¹o file sè liÖu ngay trªn mµn h×nh cña ch¬ng tr×nh. Sau khi ®·

t¹o xong, vµo Luu file so lieu ®Ó lu l¹i.

4. Sau khi cã ®îc file sè liÖu ta tiÕn hµnh Binh sai m¹ng líi. KÕt qu¶

Cao B¸ H¹

-58 -

Líp Tr¾c ®ÞaB-K48

thu ®îc thÓ hiÖn nh h×nh 3.12.

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

H×nh 3.10. Giao diÖn ch¬ng tr×nh b×nh sai líi mÆt b»ng tù do

Cao B¸ H¹

-59 -

Líp Tr¾c ®ÞaB-K48

H×nh 3.11. Më file sè liÖu

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

H×nh 3.12. KÕt qu¶ b×nh sai

3.2.2. Tæ chøc, m· ho¸ file d÷ liÖu

§Ó cho ch¬ng tr×nh m¸y tÝnh cã thÓ ®äc vµ hiÓu ®îc bµi to¸n tr¾c ®Þa

th× tríc hÕt chóng ta ph¶i m· hãa sè liÖu cña m¹ng líi tr¾c ®Þa ®ã díi d¹ng

c¸c file d÷ liÖu vµ lu chóng trong m¸y tÝnh. C¸c ®èi tîng thµnh phÇn cña

mét m¹ng líi tr¾c ®Þa tù do bao gåm ®iÓm (täa ®é), trÞ ®o gãc, trÞ ®o dµi, trÞ

®o ph¬ng vÞ (®èi víi líi mÆt b»ng) vµ ®é cao, trÞ ®o chªnh cao (®èi víi líi

®é cao) ®îc m« t¶ b»ng c¸c cÊu tróc nh sau:

3.2.2.1. Tæ chøc file sè liÖu líi mÆt b»ng thi c«ng

®iÓm míi ®¸nh sè tríc, ®iÓm ®Þnh vÞ ®¸nh sè sau (nÕu trong líi cã cã ®iÓm

gèc th× ®iÓm gèc ®îc ®¸nh sè sau cïng).

b. §a vµo c¸c tham sè ®Æc trng cña líi

- Tªn líi.

Cao B¸ H¹

-60 -

Líp Tr¾c ®ÞaB-K48

- Sè ®iÓm trong líi, sè lîng trÞ ®o gãc, trÞ ®o c¹nh, trÞ ®o ph¬ng vÞ.

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

- C¸c ®Æc trng ®é chÝnh x¸c: sai sè ®o gãc, sai sè ®o c¹nh.

c. Vµo tªn ®iÓm

d. Täa ®é gÇn ®óng c¸c ®iÓm líi

e. M· ho¸ trÞ ®o

- TrÞ ®o gãc: ®iÓm tr¸i, ®iÓm gi÷a, ®iÓm ph¶i, gi¸ trÞ gãc

- TrÞ ®o c¹nh: ®iÓm tríc, ®iÓm sau, gi¸ trÞ c¹nh

- TrÞ ®o ph¬ng vÞ: ®iÓm tríc, ®iÓm sau, gi¸ trÞ ph¬ng vÞ

LUOI THI CONG THUY DIEN BAN LA (NGHE AN)-DO THANG 6-1996

5 10 59 34 0 0.004 0.9 0.9 0.002 0.000002 TC-01 TC-02 TC-03 TC-04 TC-05 TC-06 TC-07 TC-08 TC-09 TC-10 TD-01 TD-02 TD-03 TD-04 TG-04 1 2140216.532 446041.4998 2 2140469.677 445462.9441 3 2140143.649 445322.9269 13 2139752.253 445578.9874 14 2139270.864 446191.4102 15 2138675.031 446572.6930 6 1 7 6 55 30.0 7 1 8 11 6 32.7 8 1 5 10 53 18.3 5 1 4 29 43 23.9 4 1 3 40 31 41.6 6 9 10 14 21 37.5 9 10 8 39 40 9.5 12 3 1 1 47 10.5 11 4 12 54 38 46.8 12 4 1 5 25 22.2 1 2 631.512 1 3 722.259 1 4 756.497 13 1 655.340 13 6 567.896 6 14 595.090 14 10 378.385 10 15 876.613

VÝ dô file sè liÖu líi mÆt b»ng thi c«ng:

3.2.2.1. Tæ chøc file sè liÖu líi ®é cao thi c«ng

a. TiÕn hµnh ®¸nh sè c¸c ®iÓm líi víi quy t¾c ®iÓm míi ®¸nh sè tríc,

®iÓm ®Þnh vÞ ®¸nh sè sau (nÕu trong líi cã cã ®iÓm gèc th× ®iÓm gèc ®îc

®¸nh sè sau cïng).

b. §a vµo c¸c tham sè ®Æc trng cña líi

- Tªn líi.

Cao B¸ H¹

-61 -

Líp Tr¾c ®ÞaB-K48

- Sè ®iÓm trong líi, sè lîng trÞ ®o chªnh cao.

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

c. Vµo tªn ®iÓm

d. §é cao gÇn ®óng c¸c ®iÓm líi

e. M· ho¸ trÞ ®o: §iÓm tríc, ®iÓm sau, gi¸ trÞ chªnh cao ®o.

luoi thuc nghiem luoi do cao thi cong 3 5 12 NM-1 NM-2 NM-3 NM-4 NM-5 TC-04 TC-05 TC-12 7456.26 12625.75 9250.52 6 1 615.42 2 6 2 189.51 2 1 2 -425.16 6 1 8 1180.22 4 1 3 1381.65 6 7 2 -4975.42 4 3 2 -1806.24 2 4 3 909.65 2 8 4 -707.37 2 4 5 1739.26 4 3 5 830.33 2 7 5 -2338.15 6

VÝ dô file sè liÖu líi ®é cao thi c«ng:

3.2.3. C¸c ch¬ng tr×nh nguån

Ch¬ng tr×nh chÝnh cã nhiÖm vô ®iÒu khiÓn qu¸ tr×nh xuÊt nhËp d÷ liÖu

vµ tÝnh to¸n b×nh sai th«ng qua viÖc gäi c¸c ch¬ng tr×nh con.

Ch¬ng tr×nh ®îc viÕt víi 5 modul chÝnh lµ:

- B×nh sai líi mÆt b»ng truyÒn thèng

- B×nh sai líi mÆt b»ng tù do

- B×nh sai líi ®é cao truyÒn thèng

- B×nh sai líi ®é cao tù do

- Ch¬ng tr×nh tÝnh chuyÓn to¹ ®é

C¸c ch¬ng tr×nh nguån sÏ ®îc chóng t«i giíi thiÖu cô thÓ ë phÇn phô lôc.

3.3. tÝnh to¸n thùc nghiÖm

Trªn c¬ së c¸c ch¬ng tr×nh b×nh sai ®· lËp ®îc, trong phÇn nµy chóng

t«i tiÕn hµnh thùc nghiÖm tÝnh to¸n cho m¹ng líi thi c«ng c«ng tr×nh cã trong

Cao B¸ H¹

-62 -

Líp Tr¾c ®ÞaB-K48

thùc tÕ s¶n xuÊt.

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

3.3.1. Thùc nghiÖm tÝnh to¸n líi mÆt b»ng thi c«ng

M¹ng líi ®îc thùc nghiÖm lµ líi thi c«ng thuû ®iÖn B¶n L¶ (NghÖ An) ®o

gåm 15 ®iÓm TC-01 TC-02 TC-03 TC-04 TC-05 TC-06 TC-07 TC-08

TC-09 TC-10 TD-01 TD-02 TD-03 TD-04 TG-04

Líi ®o 59 gãc, 34 c¹nh

Sai sè ®o gãc m = 0.9”

Sai sè ®o c¹nh mS= 2 + 2D(ppm) (mm)

Líi cã sè khuyÕt d =3 (d¹ng [x, y, ])

§å h×nh líi: (h×nh 3.13)

KET QUA BINH SAI

LUOI THI CONG THUY DIEN BAN LA (NGHE AN)-DO THANG 6-1996

=============000==============

I. SO LIEU KHOI TINH =====================

-So diem dinh vi : 5 -So diem can xac dinh : 10 -So luong goc do : 59 -So luong canh do : 34

Cao B¸ H¹

-63 -

Líp Tr¾c ®ÞaB-K48

H×nh 3.13. Líi khèng chÕ thi c«ng thuû ®iÖn B¶n L¶ (NghÖ An)

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

II.TOA DO DIEM DINH VI

======================

================================================================== | S | TEN | TOA DO | | | T | |---------------------------------| GHI CHU | | T | DIEM | X(m) | Y(m) | | |-----|-------|----------------|----------------|----------------| | 11 |TD-01 | 2140321.570 | 445327.245 | | | 12 |TD-02 | 2140228.376 | 445959.789 | | | 13 |TD-03 | 2139752.253 | 445578.987 | | | 14 |TD-04 | 2139270.864 | 446191.410 | | | 15 |TG-04 | 2138675.031 | 446572.693 | | ==================================================================

III.KET QUA PHAN TICH DO ON DINH CUA CAC MOC =========================================

-.002|

===================================================================== | S | TEN | TOA DO | lech k/c | | T | |-------------------------------|-----------------------| | T | DIEM | dX(m) | dY(m) | ds(cm) | |---|-------|---------------|---------------|-----------------------| -.003| .000| .003 | |11 |TD-01 | |12 |TD-02 | .000| .004| .004 | |13 |TD-03 | .001| .001| .001 | -.006| .006 | |14 |TD-04 | .004 | |15 |TG-04 | .004| .001| =====================================================================

IV.KET QUA TRI DO SAU BINH SAI ===============================

A.TRI DO GOC NGANG SAU BINH SAI

===================================================================== | SO | TEN-DINH | GIA TRI GOC | HIEU | TRI GOC SAU | | THU|---------------------| DO | CHINH | BINH SAI | | TU | Trai-Giua-Phai | Do-Phut-Giay| Giay | Do-Phut-Giay| |----|---------------------|-------------|------------|-------------| | 1 |TC-06 TC-01 TC-07 | 6 55 30.00| .56 | 6 55 30.56| -.57 | 11 6 32.13| | 2 |TC-07 TC-01 TC-08 | 11 6 32.70| | 3 |TC-08 TC-01 TC-05 | 10 53 18.30| 1.35 | 10 53 19.65| | 4 |TC-05 TC-01 TC-04 | 29 43 23.90| .80 | 29 43 24.70| | 5 |TC-04 TC-01 TC-03 | 40 31 41.60| -1.74 | 40 31 39.86| -.04 | 29 25 23.76| | 6 |TC-03 TC-01 TC-02 | 29 25 23.80| | 7 |TC-01 TC-02 TC-04 | 62 21 32.20| .09 | 62 21 32.29| | 8 |TC-04 TC-02 TC-03 | 27 15 1.80| 1.94 | 27 15 3.74| | 9 |TC-02 TC-03 TC-01 | 60 57 59.60| .60 | 60 58 .20| |10 |TC-01 TC-03 TC-06 | 24 48 51.60| .22 | 24 48 51.82| |11 |TC-06 TC-03 TC-05 | 37 17 6.30| .51 | 37 17 6.81| -.47 | 11 13 29.73| |12 |TC-05 TC-03 TC-04 | 11 13 30.20| -1.19 | 18 27 27.71| |13 |TC-03 TC-04 TC-02 | 18 27 28.90| -.52 | 47 41 24.08| |14 |TC-02 TC-04 TC-01 | 47 41 24.60| -.56 | 28 52 5.24| |15 |TC-01 TC-04 TC-06 | 28 52 5.80| |16 |TC-06 TC-04 TC-10 | 25 7 20.10| -.35 | 25 7 19.75| |17 |TC-03 TC-05 TC-01 | 47 38 56.50| .31 | 47 38 56.81| |18 |TC-01 TC-05 TC-06 | 18 0 47.00| .25 | 18 0 47.25| |19 |TC-06 TC-05 TC-10 | 43 7 18.60| .30 | 43 7 18.90| |20 |TC-10 TC-05 TC-08 | 93 33 31.40| .72 | 93 33 32.12| |21 |TC-10 TC-06 TC-09 | 22 7 11.40| .59 | 22 7 11.99|

Cao B¸ H¹

-64 -

Líp Tr¾c ®ÞaB-K48

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

-.27 | 18 58 32.23| |22 |TC-09 TC-06 TC-07 | 18 58 32.50| |23 |TC-07 TC-06 TC-05 | 35 41 49.30| -.94 | 35 41 48.36| |24 |TC-05 TC-06 TC-04 | 40 34 42.40| .29 | 40 34 42.69| .34 | 36 28 26.44| |25 |TC-04 TC-06 TC-03 | 36 28 26.10| -.72 | 56 0 41.28| |26 |TC-03 TC-06 TC-01 | 56 0 42.00| -.53 | 4 18 50.67| |27 |TC-01 TC-07 TC-06 | 4 18 51.20| |28 |TC-06 TC-07 TC-10 | 50 17 15.00| -.31 | 50 17 14.69| |29 |TC-10 TC-07 TC-09 | 90 51 1.50| .07 | 90 51 1.57| |30 |TC-09 TC-07 TC-08 | 63 54 37.90| .37 | 63 54 38.27| |31 |TC-08 TC-07 TC-01 | 150 38 14.40| .40 | 150 38 14.80| |32 |TC-05 TC-08 TC-01 | 14 25 1.10| .97 | 14 25 2.07| |33 |TC-01 TC-08 TC-07 | 18 15 12.00| 1.08 | 18 15 13.08| -.72 | 10 0 19.58| |34 |TC-07 TC-08 TC-10 | 10 0 20.30| -.10 | 46 13 45.90| |35 |TC-10 TC-08 TC-09 | 46 13 46.00| -1.75 | 59 51 16.25| |36 |TC-08 TC-09 TC-07 | 59 51 18.00| |37 |TC-07 TC-09 TC-06 | 19 53 12.20| -.70 | 19 53 11.50| |38 |TC-06 TC-09 TC-10 | 14 21 37.50| .23 | 14 21 37.73| |39 |TC-09 TC-10 TC-08 | 39 40 9.50| -.89 | 39 40 8.61| |40 |TC-08 TC-10 TC-07 | 15 14 .50| .08 | 15 14 .58| |41 |TC-07 TC-10 TC-05 | 28 31 53.30| -.73 | 28 31 52.57| |42 |TC-05 TC-10 TC-04 | 22 34 43.30| .24 | 22 34 43.54| |43 |TC-04 TC-10 TC-06 | 37 30 24.00| .97 | 37 30 24.97| |44 |TC-07 TG-04 TD-04 | 0 49 49.60| -1.36 | 0 49 48.24| |45 |TD-04 TG-04 TC-10 | 24 49 4.20| .45 | 24 49 4.65| |46 |TG-04 TC-10 TD-04 | 51 41 30.50| -.28 | 51 41 30.22| |47 |TD-04 TC-10 TC-06 | 91 17 4.50| .38 | 91 17 4.88| |48 |TC-06 TD-04 TC-10 | 49 14 38.00| 1.10 | 49 14 39.10| -.99 | 39 28 16.01| |49 |TC-10 TC-06 TD-04 | 39 28 17.00| -.32 | 86 18 58.98| |50 |TD-03 TC-06 TC-01 | 86 18 59.30| -.87 | 1 12 36.33| |51 |TC-04 TC-01 TD-03 | 1 12 37.20| -.06 | 39 19 3.54| |52 |TD-03 TC-01 TC-03 | 39 19 3.60| -.19 | 6 14 15.81| |53 |TD-02 TD-03 TC-01 | 6 14 16.00| -.14 | 33 49 37.66| |54 |TC-01 TD-03 TC-06 | 33 49 37.80| |55 |TD-03 TD-02 TC-03 | 43 46 9.50| -.78 | 43 46 8.72| |56 |TD-02 TD-01 TC-04 | 65 13 50.30| .01 | 65 13 50.31| |57 |TD-02 TC-03 TC-01 | 1 47 10.50| .13 | 1 47 10.63| |58 |TD-01 TC-04 TD-02 | 54 38 46.80| .01 | 54 38 46.81| |59 |TD-02 TC-04 TC-01 | 5 25 22.20| -.22 | 5 25 21.98| =====================================================================

B.TRI DO CANH SAU BINH SAI

=========================================================== | SO | TEN-CANH | CHIEU DAI | HIEU | CHIEU DAI | | THU|----------------| DO | CHINH | SAU BINH SAI | | TU | DAU-CUOI | (m) | (m) | (m) | |----|----------------|------------|-------|--------------| | 1 |TC-01 TC-02 | 631.512 | .002 | 631.514 | | 2 |TC-01 TC-03 | 722.259 | .001 | 722.260 | | 3 |TC-01 TC-04 | 756.497 | .000 | 756.497 | | 4 |TC-01 TC-05 | 863.707 | -.003 | 863.704 | | 5 |TC-01 TC-06 | 365.574 | .003 | 365.577 | | 6 |TC-01 TC-07 | 947.217 | .000 | 947.217 | 354.822 | .002 | 354.824 | | 7 |TC-02 TC-03 | | 8 |TC-02 TC-04 | 802.205 | .003 | 802.208 | | 9 |TC-03 TC-04 | 513.163 | .002 | 513.165 | |10 |TC-03 TC-05 | 919.822 | .000 | 919.822 | |11 |TC-03 TC-06 | 859.944 | -.002 | 859.942 | |12 |TC-04 TC-06 | 646.638 | -.002 | 646.636 | |13 |TC-04 TC-10 | 943.152 | -.001 | 943.151 | 571.749 | |14 |TC-05 TC-06 | 571.751 | -.002 |

Cao B¸ H¹

-65 -

Líp Tr¾c ®ÞaB-K48

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

|15 |TC-05 TC-10 | 642.179 | .003 | 642.182 | |16 |TC-05 TC-08 | 655.290 | .007 | 655.297 | |17 |TC-06 TC-07 | 585.968 | -.001 | 585.967 | |18 |TC-06 TC-09 | 1080.864 | -.002 | 1080.862 | |19 |TC-06 TC-10 | 450.892 | .000 | 450.892 | |20 |TC-07 TC-08 | 582.665 | .000 | 582.665 | |21 |TC-07 TC-09 | 560.142 | -.002 | 560.140 | |22 |TC-07 TC-10 | 385.281 | -.002 | 385.279 | |23 |TC-08 TC-09 | 605.141 | .000 | 605.141 | |24 |TC-08 TC-10 | 945.543 | .002 | 945.545 | |25 |TC-09 TC-10 | 684.547 | -.001 | 684.546 | |26 |TD-01 TC-04 | 679.750 | .000 | 679.750 | |27 |TC-03 TD-02 | 642.480 | -.003 | 642.477 | |28 |TG-04 TC-07 | 723.385 | .001 | 723.386 | | 711.817 | .000 | 711.817 | |29 |TD-02 TC-04 |30 |TD-03 TC-01 | 655.340 | .002 | 655.342 | |31 |TD-03 TC-06 | 567.896 | -.002 | 567.894 | |32 |TC-06 TD-04 | 595.090 | -.002 | 595.088 | |33 |TD-04 TC-10 | 378.385 | .001 | 378.386 | |34 |TC-10 TG-04 | 876.613 | -.001 | 876.612 | ===========================================================

V.KET QUA TOA DO DIEM SAU BINH SAI ====================================

ELIP SAI SO

=========================================================================================== | S | TEN | TOA DO | SAI SO VI TRI DIEM | | | T | |-------------------------|--------------------|------------------------------| | T | DIEM | X(m) | Y(m) |Mx(cm)|My(cm)|Md(cm)| E | F | Goc dinh huong | |---|-------|------------|------------|------|------|------|------------------------------| | 1 |TC-01 | 2140216.534| 446041.501| .14 | .16 | .21 | 1.59 | 1.39 | 134 | 17 | | 2 |TC-02 | 2140469.679| 445462.945| .19 | .23 | .30 | 2.57 | 1.54 | 11 | 6 | | 3 |TC-03 | 2140143.650| 445322.928| .19 | .16 | .25 | 2.03 | 1.44 | 10 | 53 | | 4 |TC-04 | 2139669.435| 445519.035| .13 | .17 | .22 | 1.71 | 1.32 | 29 | 43 | | 5 |TC-05 | 2139378.329| 445833.179| .14 | .20 | .24 | 1.98 | 1.39 | 40 | 31 | | 6 |TC-06 | 2139863.357| 446135.908| .13 | .15 | .20 | 1.58 | 1.20 | 29 | 25 | | 7 |TC-07 | 2139278.629| 446173.993| .14 | .20 | .24 | 2.10 | 1.23 | 62 | 21 | | 8 |TC-08 | 2138735.846| 445962.131| .18 | .31 | .36 | 3.14 | 1.82 | 27 | 15 | | 9 |TC-09 | 2138866.236| 446553.057| .22 | .29 | .37 | 3.23 | 1.71 | 60 | 57 | |10 |TC-10 | 2139543.540| 446453.746| .15 | .15 | .21 | 1.72 | 1.26 | 24 | 48 | |11 |TD-01 | 2140321.567| 445327.245| .20 | .18 | .27 | 1.98 | 1.79 | 37 | 17 | |12 |TD-02 | 2140228.376| 445959.793| .17 | .14 | .22 | 1.80 | 1.25 | 11 | 13 | |13 |TD-03 | 2139752.254| 445578.988| .17 | .18 | .25 | 1.85 | 1.66 | 18 | 27 | |14 |TD-04 | 2139270.862| 446191.404| .16 | .14 | .21 | 1.75 | 1.20 | 47 | 41 | |15 |TG-04 | 2138675.035| 446572.694| .18 | .18 | .25 | 2.02 | 1.51 | 28 | 52 | ===========================================================================================

VI. CAC YEU TO TUONG HO CUA LUOI ================================

===================== | No | Ten canh |----|--------------| | 1 |TC-01 TC-02 | | 2 |TC-01 TC-03 | | 3 |TC-01 TC-04 | | 4 |TC-01 TC-05 | | 5 |TC-01 TC-06 | | 6 |TC-01 TC-07 | | 7 |TC-02 TC-03 | | 8 |TC-02 TC-04 | | 9 |TC-03 TC-04 | | 10 |TC-03 TC-05 | | 11 |TC-03 TC-06 | | 12 |TC-04 TC-06 | | 13 |TC-04 TC-10 | | 14 |TC-05 TC-06 | | 15 |TC-05 TC-10 | | 16 |TC-05 TC-08 | | 17 |TC-06 TC-07 | ============================================================= | Chieu dai | Phuong vi |Ma(")| Ms(m)| Ms/S | Mth | -----------|-------------|-----|------|--------------|------| 631.514| 293 37 53.91| .77| .001| 1: 458000 | .003| 722.260| 11 6 32.70| .65| .001| 1: 570000 | .003| 756.497| 10 53 18.30| .59| .001| 1: 605000 | .003| 863.704| 29 43 23.90| .54| .001| 1: 594000 | .003| 365.577| 40 31 41.60| .68| .001| 1: 321000 | .002| 947.217| 29 25 23.80| .51| .001| 1: 631000 | .003| 354.824| 62 21 32.20| .84| .001| 1: 250000 | .002| 802.208| 27 15 1.80| .70| .002| 1: 507000 | .003| 513.165| 60 57 59.60| .76| .001| 1: 424000 | .002| 919.822| 24 48 51.60| .59| .002| 1: 600000 | .003| 859.942| 37 17 6.30| .60| .001| 1: 663000 | .003| 646.636| 11 13 30.20| .59| .001| 1: 524000 | .002| 943.151| 18 27 28.90| .47| .001| 1: 652000 | .003| 571.749| 47 41 24.60| .61| .001| 1: 448000 | .002| 642.182| 28 52 5.80| .57| .001| 1: 497000 | .002| 655.297| 25 7 20.10| .67| .002| 1: 393000 | .003| 585.967| 47 38 56.50| .56| .001| 1: 486000 | .002|

Cao B¸ H¹

-66 -

Líp Tr¾c ®ÞaB-K48

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

| 18 |TC-06 TC-09 | 1080.862| 18 0 47.00| .55| .002| 1: 669000 | .003| | 19 |TC-06 TC-10 | 450.892| 43 7 18.60| .51| .001| 1: 453000 | .001| | 20 |TC-07 TC-08 | 582.665| 93 33 31.40| .63| .001| 1: 405000 | .002| | 21 |TC-07 TC-09 | 560.140| 22 7 11.40| .67| .001| 1: 399000 | .002| | 22 |TC-07 TC-10 | 385.279| 18 58 32.50| .66| .001| 1: 346000 | .002| | 23 |TC-08 TC-09 | 605.141| 35 41 49.30| .77| .001| 1: 415000 | .003| | 24 |TC-08 TC-10 | 945.545| 40 34 42.40| .61| .002| 1: 615000 | .003| | 25 |TC-09 TC-10 | 684.546| 36 28 26.10| .71| .001| 1: 488000 | .003| | 26 |TD-01 TC-04 | 679.750| 56 0 42.00| .87| .002| 1: 295000 | .004| | 27 |TC-03 TD-02 | 642.477| 4 18 51.20| .79| .002| 1: 362000 | .003| | 28 |TG-04 TC-07 | 723.386| 50 17 15.00| .95| .002| 1: 313000 | .004| | 29 |TD-02 TC-04 | 711.817| 90 51 1.50| .65| .002| 1: 397000 | .003| | 30 |TD-03 TC-01 | 655.342| 63 54 37.90| .73| .002| 1: 351000 | .003| | 31 |TD-03 TC-06 | 567.894| 150 38 14.40| .76| .002| 1: 320000 | .003| | 32 |TC-06 TD-04 | 595.088| 14 25 1.10| .52| .001| 1: 430000 | .002| | 33 |TD-04 TC-10 | 378.386| 18 15 12.00| .61| .001| 1: 296000 | .002| | 34 |TC-10 TG-04 | 876.612| 10 0 20.30| .69| .002| 1: 360000 | .004| ==================================================================================

VII.KET LUAN ============

1. Sai so trung phuong trong so don vi mo = .89 " - TC-07 ma = .95 " 2. Phuong vi yeu nhat TG-04 3. Canh yeu nhat TC-02 - TC-03 ms/S = 1/250000 4. Diem yeu nhat TC-09 M = .37(cm)

Nguoi thuc hien: Cao Ba Ha Lop : Trac dia B - K48 TRUONG DAI HOC MO - DIA CHAT

3.3.2. Thùc nghiÖm tÝnh to¸n líi ®é cao thi c«ng

M¹ng líi ®îc thùc nghiÖm gåm 3 mèc cÊp c¬ së vµ 5 mèc míi.

Líi ®o 12 chªnh cao.

KET QUA BINH SAI LUOI DO CAO ===========* * *============

I.SO LIEU KHOI TINH =================== So diem do cao goc : 3 So diem can xac dinh : 5 So luong chenh cao do : 12

II. DO CAO DIEM DINH VI =======================

-------------------------------------------- | S | TEN | DO CAO | | T | |----------------------------| | T | DIEM | H(mm) Ghi chu | |------------------------------------------| | | 6 |TC-04 | 7456.26 | | 7 |TC-05 | 12625.75 | | | 8 |TC-12 | 9250.52 | | --------------------------------------------

Cao B¸ H¹

-67 -

Líp Tr¾c ®ÞaB-K48

Líi cã sè khuyÕt d =1.

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

III. DO LECH CAO DO CUA CAC DIEM DINH VI ======================================== -------------------------------------------- | S | TEN | DO lech | | T | |----------------------------| | T | DIEM | dH(mm) Ghi chu | |------------------------------------------| | 6 |TC-04 | 1.27 | | | 7 |TC-05 | -3.10 | | | 8 |TC-12 | 1.83 | | --------------------------------------------

IV.KET QUA TRI DO SAU BINH SAI ============================== TRI DO CHENH CAO SAU BINH SAI -----------------------------

- NM-2 | -425.16 | - TC-12 | 1180.22 | - NM-3 | 1381.65 |

=================================================================== | SO | TEN - CANH | GIA TRI CHENH | HIEU | TRI CHENH CAO | Mh | | THU| ------------- | CAO DO | CHINH | BINH SAI | | | TU | DAU - CUOI | (mm) | (mm) | (mm) |(mm)| ------------------------------------------------------------------- | 1 | TC-04 - NM-1 | 615.42 | -.34| 615.08 | .13| | 2 | TC-04 - NM-2 | 189.51 | .34| 189.85 | .18| -.07| | 3 | NM-1 -425.23 | .19| -.48| 1179.74 | .29| | 4 | NM-1 -.24| 1381.41 | .26| | 5 | NM-1 -4975.27 | .32| -4975.42 | .15| | 6 | TC-05 - NM-2 | -.39| - NM-2 | | 7 | NM-3 -1806.63 | .27| -1806.24 | -.38| 909.27 | .29| - NM-3 | 909.65 | | 8 | NM-4 | 9 | TC-12 - NM-4 | -707.61 | .34| -.24| -707.37 | - NM-5 | 1739.26 | .28| 1739.54 | .37| | 10 | NM-4 -.06| 830.27 | .32| - NM-5 | 830.33 | | 11 | NM-3 -2338.37 | .50| -.22| -2338.15 | | 12 | TC-05 - NM-5 | -------------------------------------------------------------------

V.DO CAO DIEM SAU BINH SAI ==========================

========================================================= | S | TEN | DO CAO | SAI SO | | | T | | ------------------------ | GHI CHU | | T | DIEM | (mm) | (mm) | --------------------------------------------------------| | 1 | NM-1 | 8072.61 | .32 | | | 2 | NM-2 | 7647.38 | .28 | | | 3 | NM-3 | 9454.01 | .31 | | | 4 | NM-4 | 8544.74 | .34 | | | 5 | NM-5 | 10284.28 | .37 | | | 6 | TC-04 | 7457.53 | .29 | | | 7 | TC-05 | 12622.65 | .35 | | | 8 | TC-12 | 9252.35 | .32 | | ---------------------------------------------------------

DO CHINH XAC DO DAC -------------------

Sai so trung phuong trong so don vi: .28mm

GHI CHU :

- Nguoi tinh : Cao Ba Ha - Lop trac dia BK48 - Truong dai hoc Mo Dia chat

Cao B¸ H¹

-68 -

Líp Tr¾c ®ÞaB-K48

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

KÕt luËn

Tõ kÕt qu¶ nghiªn cøu lý thuyÕt vµ thuËt to¸n øng dông, qua qu¸ tr×nh

thùc hiÖn ®å ¸n t«i cã mét sè kÕt luËn nh sau:

1. ViÖc øng dông ph¬ng ph¸p b×nh sai líi tù do lµ gi¶i ph¸p thÝch hîp

cho c«ng t¸c xö lý sè liÖu m¹ng líi thi c«ng c«ng tr×nh.

2. Trong ®å ¸n ®· kh¶o s¸t ph¬ng ph¸p vµ quy tr×nh tÝnh to¸n b×nh sai

líi tù do. §· x¸c ®Þnh, lùa chän thuËt to¸n hîp lý ®Ó b×nh sai m¹ng líi thi

c«ng c«ng tr×nh (líi mÆt b»ng thi c«ng vµ líi ®é cao thi c«ng).

3. Trªn c¬ së kh¶o s¸t lý thuyÕt chóng t«i ®· thµnh lËp ®îc ch¬ng

tr×nh tÝnh to¸n trªn m¸y vi tÝnh. §· thùc hiÖn tÝnh to¸n thùc nghiÖm trªn mét

sè m¹ng líi, kÕt qu¶ xö lý sè liÖu ®· ®îc so s¸nh víi mét sè phÇn mÒm

kh¸c vµ ®· kh¼ng ®Þnh ®îc tÝnh ®óng ®¾n cña thuËt to¸n vµ ch¬ng tr×nh mµ

chóng t«i ®· thµnh lËp ®îc.

Do kh¶ n¨ng vµ thêi gian nghiªn cøu cßn nhiÒu h¹n chÕ, tuy b¶n ®å ¸n ®·

hoµn thµnh, nhng kh«ng tr¸nh khái nhiÒu thiÕu sãt. V× vËy, t«i rÊt mong

®îc sù gióp ®ì vµ ®ãng gãp ý kiÕn cña c¸c thÇy, c« gi¸o, c¸c c¸n bé chuyªn

ngµnh vµ c¸c b¹n ®ång nghiÖp ®Ó kiÕn thøc cña t«i ®îc më réng h¬n.

bé m«n Tr¾c ®Þa c«ng tr×nh, khoa Tr¾c ®Þa, ngêi ®· tËn t×nh híng dÉn t«i

trong suèt qu¸ tr×nh thùc hiÖn ®å ¸n.

Hµ Néi, th¸ng 6 - 2008

Sinh viªn

Cao B¸ H¹

-69 -

Líp Tr¾c ®ÞaB-K48

Cao B¸ H¹

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

Phô lôc

c¸c ch¬ng tr×nh nguån

$debug $large c CHUONG TRINH BINH SAI LUOI MAT BANG THI CONG c Ho va ten :Cao Ba Ha c Lop : Trac dia B - K48

Implicit Real *8(a-h, o-z) Character ff*30 Character Khd(100)*7 Character Tr*8, Tenct*100 Common /v1/ X(100),Y(100),It(500),Ig(500),Ip(500),

*Id(500),Iph(500),giay(500),Id1(500),Iph1(500),giay1(500)

Common /v3/ Goc(500),Kd(500),Kc(500),Canh(500) Common /v2/ Hv(200),Ptc(5000) Common /v4/ Idfv(500),Icfv(500),Gocfv(500) Dimension B(50,3),C(50,3),BB(5000),CC(5000),Sa(500) Dimension Ktt(100),RLV(100),Q1(50,50),Ds(500) Dimension Sm(500),S(500),SSd(500),Sth(500) Dimension Xg(100),Yg(100),Xe(500),Ye(500) Dimension E(100),F(100),Ph(100),ZN(100),ZM(100),Se(1000) Dimension X2(500),Y2(500),Beta(500)

Write(*,'(a\)') ' Nhap ten file du lieu : ' Read (*,'(a)') ff Open (1,file=ff,status='old') Write(*,'(a\)') ' Nhap ten file ket qua : ' Read(*, '(a)') ff Open(4,file= ff,status='new') Write(*,'(a\)') ' Nhap ten file *.dxf : ' Read(*,'(a)') ff Open(6,file= ff,status='new') bk=10d0 cch=40d0 b1= 1.d0 Pi= 4.d0*dAtan(b1) Pi2= 2.d0*Pi Ro= 3600.d0*180.d0/Pi dv=1000.d0 Df=0.000001

Read (1,'(a)') Tenct Read (1,*) Ng,Nxd,Ngoc,Ncanh,Nfv, sma Write (4,1) Tenct,Ng,Nxd,Ngoc,Ncanh

1 Format (// 31X,'KET QUA BINH SAI'/

* 10X,A100/ * 24X,'=============000=============='///// * 15X,'I. SO LIEU KHOI TINH'/ * 15X,'====================='// * 18X, '-So diem dinh vi : ' ,I3/ * 18X, '-So diem can xac dinh : ' ,I3/ * 18X, '-So luong goc do : ' ,I3/ * 18X, '-So luong canh do : ' ,I3/)

Read(1,*) Ssg,Ssfv,a,b1

Cao B¸ H¹

-70 -

Líp Tr¾c ®ÞaB-K48

1. Ch¬ng tr×nh b×nh sai líi mÆt b»ng thi c«ng

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

Ndi=(Nxd+Ng)

Read(1,2)(Khd(I),I=1,Ndi) Format(10A7)

hk=Khd(nxd+1) Do 3 M=1, Ndi Read (1,*) M,X(M),Y(M) Xy=X(nxd+1) Yy=Y(nxd+1)

3 Continue

Write (4, 4)

4 Format (/15x, 'II.TOA DO DIEM DINH VI'/

* 15x, '======================'// * 10x, 66('=')/ * 10x, '| S | TEN | TOA DO |' *' |'/ * 10X, '| T | |---------------------------------|' *' GHI CHU |'/ * 10X, '| T | DIEM | X(m) | Y(m) |' *' |'/ * 10X, '|-----|-------|----------------|----------------|' *'----------------|')

N=(Nxd+1) Do 5 I=N, Ndi Write(4,6) I,Khd(I),X(I),Y(I)

6 Format(10x,'|',I3,' |',A7,'|',F15.3,' |',F15.3,' |'

*' |')

5 Continue

Write(4,7)

7 Format(10x,66('=')) Do 8 M=1, Ngoc Read (1,*) It(m),Ig(m),Ip(m),Id(m),Iph(m),giay(m) Goc(m)= (Id(m)*3600.d0+Iph(m)*60.d0+giay(m))/Ro

Continue

Do 9 M= 1, Ncanh Read (1,*) Kd(m),Kc(m),canh(m)

9 Continue

Do 10 M=1,Nfv Read(1,*) Idfv(m),Icfv(m),Id(m),Iph(m),giay(m) Gocfv(m)=(Id(m)*3600.d0+Iph(m)*60.d0+giay(m))/Ro

10 Continue

Ian= Ndi*2 KK =Ian*(Ian-1)/2+Ian Ms=Ian*(Ian+1)/2 Do 101 IQ=1,Ms PTC(IQ)=0.d0

101 Continue

If(Ngoc.eq.0.d0) Goto 102 Do 103 M=1,Ngoc I= Ig(M) J= It(M) K= Ip(M) Call dSHCG(Ro,Pi2,I,J,K,M,Ian) P= 1.d0/(ssg**2) Call dPTC(Ian, P)

103 Continue

102 If(Ncanh.eq.0.d0) Goto 104

Cao B¸ H¹

-71 -

Líp Tr¾c ®ÞaB-K48

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

Do 105 M= 1,Ncanh I= Kd(M) J= Kc(M) Call Dshcc(M, I, J, Ian) P=1.d0/((a+b1*Canh(M))**2) Call dPTC(Ian, P)

105 Continue

104 If(Nfv.EQ.0.d0) Goto 741

Do 106 M=1,Nfv I=Idfv(m) J=Icfv(m) Call dSHCFV(Ro,Pi2,I,J,M,Ian) P=1.d0/(Ssfv**2) Call dPTC(Ian, P)

106 Continue

741 Sx=0.d0 Sy=0.d0 N1=Ndi-Ng M1=N1+1 Do 1111 I=M1,Ndi Sx=Sx+X(I)/Ng Sy=Sy+Y(I)/Ng

1111 Continue CC1=0.d0 Do 1112 I=M1,Ndi CC1=CC1+(X(I)-Sx)**2+(Y(I)-Sy)**2

1112 Continue

CC1=dsqrt(CC1) dm1=Ng*1.d0 dm1=1.d0/dsqrt(dm1) N0=M1*2-1 Do 1113 I=1,Ian B(I,1)=dm1*MOD(I,2) B(I,2)=dm1*MOD(I+1,2) If(Ng.eq.Ndi) Goto 1113 C(I,1)=B(I,1) C(I,2)=B(I,2) If(I.GE.N0) Goto 1113 C(I,1)=0.d0 C(I,2)=0.d0

1113 Continue

Do 1114 I=1,Ndi B(2*I-1,3)= (Y(I)-Sy)/CC1 B(2*I,3) =-(X(I)-Sx)/CC1 If(Ng.eq.Ndi) Goto 1114 C(2*I-1,3)=B(2*I-1,3) C(2*I,3) =B(2*I,3) If(I.ge.M1) Goto 1114 C(2*I-1,3)=0.d0 C(2*I,3) =0.d0

1114 Continue

KL=(Ian-1)*Ian/2+Ian Do 1115 L1=1,KL BB(L1)=0.d0 CC(L1)=0.d0

1115 Continue

Cao B¸ H¹

-72 -

Líp Tr¾c ®ÞaB-K48

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

Do 1116 I=1,Ian Do 1117 K=I,Ian J=(K-1)*K/2+I Do 1118 L=1,3 If(Ng.EQ.Ndi) Goto 1130 CC(J)=CC(J)+C(I,L)*C(K,L) 1130 BB(J)=BB(J)+B(I,L)*B(K,L) 1118 Continue 1117 Continue 1116 Continue

KL=(Ian-1)*Ian/2+Ian Do 1131 L=1,KL If(Ng.EQ.Ndi) Goto 132 PTC(L)=PTC(L)+CC(L)*10000000.d0 Goto 1131

132 PTC(L)=PTC(L)+BB(L)*10000000.d0 1131 Continue

Ls=Ian-1 Call DTDNG(Ls) Call DNDAO(Ian)

Do 800 I2=1,Ian RLV(I2)=0.d0

800 Continue

Do 801 I3=1,Ian Do 802 J3=1,Ian If(J3.GT.I3) Goto 805 K=(I3-1)*I3/2+J3 Goto 806

805 K=(J3-1)*J3/2+I3 806 RLV(I3)=RLV(I3)-PTC(K)*PTC(KL+J3) 802 Continue 801 Continue

889 Write(4, 701) 701 Format(//14x, 'III.KET QUA PHAN TICH DO ON DINH CUA CAC MOC '/

|-------------------------------|----------------

* 15x, '========================================= '// *10x,69('=')/ *10x,'| S | TEN | TOA DO | lech k/c * |'/ *10x,'| T | *-------|'/ *10x,'| T | DIEM | dX(m) | dY(m) | ds(cm) * |'/ *10x,'|---|-------|---------------|---------------|---------------- *-------|')

sdy=0.d0 DRmax=0d0 Do 989 K=(nxd+1),Ndi RX= RLV(K*2-1) RY= RLV(K*2) DR= dsqrt(RX**2+RY**2) If(DR.le.DRmax) Goto 710 DRmax=DR Tendy=Khd(K) sttmax=K Xmax=X(K)

Cao B¸ H¹

-73 -

Líp Tr¾c ®ÞaB-K48

§å ¸n tèt nghiÖp

Khoa Tr¾c ®Þa

Ymax=Y(K)

710 Write (4, 711) k,Khd(k),RX,RY,DR 711 Format (10x,'|', I2,' |' , A7,'|', F15.3,'|', F15.3, '| ',F15.3,'

* |') 989 Continue

write(4,712) 712 Format(10x,69('='))

Write(4, 820)

820 Format(//15x, 'IV.KET QUA TRI DO SAU BINH SAI'/

* 15X, '==============================='//)

If(Ngoc.eq.0.d0) Goto 514 Write(4,513)

513 Format(15X, 'A.TRI DO GOC NGANG SAU BINH SAI'//

*10x,69('=')/ *10x,'| SO | TEN-DINH ' *'| GIA TRI GOC | HIEU | TRI GOC SAU |'/ *10x,'| THU|---------------------' *'| DO | CHINH | BINH SAI |'/ *10x,'| TU | Trai-Giua-Phai ' *'| Do-Phut-Giay| Giay | Do-Phut-Giay|'/ *10x'|----|---------------------|-------------|------------' *'|-------------|')

Pvv1=0.d0 Do 810 M= 1,Ngoc Pg=1.d0/(Ssg**2) I=Ig(M) J=It(M) K=Ip(M) Call dSHCG(Ro,Pi2,I,J,K,M,Ian) V= 0.d0 Do 812 L= 1, Ian V=V + HV(L)*RLV(L)

812 Continue

V=V+HV(Ian+1) Pvv1=Pvv1+V*V*Pg Call Drado(Goc(M),Id(m),Iph(m),giay(m),Ro) Id1(m) = Id(m) Iph1(m) = Iph(m) Giay1(m)= Giay(m)+V If(Giay1(m).ge.60.d0) Goto 830 If(Giay1(m).lt.0.d0) Goto 832 Goto 860

832 II = Giay1(m)/60.d0-1

Iph1(m) = Iph1(m)+II Giay1(m)= Giay1(m)+Abs(II*60.d0) If(Iph1(m).le.0.d0) Goto 833 Goto 860

833 II = Iph1(m)/60.d0-1

Id1(m) = Id1(m)+II Iph1(m)= Iph1(m)+Abs(II*60.d0) Goto 860

830 II = Giay1(m)/60.d0

Iph1(m) = Iph1(m)+II Giay1(m)= Giay1(m)-II*60.d0 If(Iph1(m).ge.60) Goto 831 Goto 860

831 II = Iph1(m)/60.d0

Id1(m) = Id1(m)+II Iph1(m)= Iph1(m)-II*60.d0 Goto 860

Cao B¸ H¹

-74 -

Líp Tr¾c ®ÞaB-K48

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

860 Write (4,813) M,Khd(It(M)),Khd(Ig(M)),Khd(Ip(M))

* ,Id(m), Iph(m) , Giay(m), V, Id1(m), Iph1(m), Giay1(m)

813 Format ( 10x,'|', I2, ' |', 3A7, '|', I4, I3, F6.2, '|',

*F8.2,4X,'|', I4, I3, F6.2, '|' )

810 Continue

Write(4, 890) 890 Format(10x,69('=')) 514 If (Ncanh.eq.0.d0) Goto 515 919 Write(4,920) 920 Format(//15X, 'B.TRI DO CANH SAU BINH SAI'//

*10x, 59('=')/ *10x,'| SO | TEN-CANH | CHIEU DAI | HIEU | CHIEU ' *'DAI |'/ *10x,'| THU|----------------| DO | CHINH | SAU ' *'BINH SAI |'/ *10x,'| TU | DAU-CUOI | (m) | (m) | (m)' *' |'/ *10x,'|----|----------------|------------|-------|--------' *'------|') Pvv2=0.d0 Do 910 M=1,(Ncanh) I=Kd(M) J=Kc(M) Pc=1/((a+b1*Canh(m))**2) Call dSHCC(M,I,J,Ian) V=0.d0 Do 912 L=1,Ian V=V+HV(L)*RLV(L)

912 Continue

V=V+HV(Ian+1) Pvv2=Pvv2+V*V*Pc Canhbs=Canh(M)+V Write (4, 913) M,Khd(Kd(M)),Khd(Kc(M)),Canh(M),V,Canhbs

913 Format (10x,'|',I2,' |' , A7, ' ', A7, ' |', F10.3, ' |', F6.3

* ' |', F10.3, ' |')

910 Continue

Write(4, 914) 914 Format(10x,59('=')) 515 If(Nfv.eq.0.d0) Goto 1222

Write(4,516)

516 Format(//15X, 'C.TRI DO PHUONG VI SAU BINH SAI'//

*10x, 64('=')/ *10x,'| SO | TEN-HUONG | GIA TRI GOC | HIEU |' *' TRI GOC SAU |'/ *10x,'| THU|----------------| DO | CHINH |' *' BINH SAI |'/ *10x,'| TU | DAU-CUOI | Do-Phut-Giay| Giay |' *' Do-Phut-Giay|'/ *10x,'|----|----------------|-------------|------------|' *'-------------|')

Pvv3=0.d0 Do 310 M= 1,Nfv Pfv=1/(Ssfv**2) I=Idfv(M) J=Icfv(M) Call dSHCFV(Ro,Pi2,I,J,M,Ian) V= 0.d0 Do 312 L= 1, Ian V=V + HV(L)*RLV(L)

312 Continue

V=V+HV(Ian+1)

Cao B¸ H¹

-75 -

Líp Tr¾c ®ÞaB-K48

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

Pvv3=Pvv3+V*V*Pfv Call Drado(Gocfv(M),Id(m),Iph(m),giay(m),Ro) Id1(m) = Id(m) Iph1(m) = Iph(m) Giay1(m)= Giay(m)+V If(Giay1(m).ge.60.d0) Goto 330 If(Giay1(m).lt.0.d0) Goto 332 Goto 360

332 II = Giay1(m)/60.d0-1

Iph1(m) = Iph1(m)+II Giay1(m)= Giay1(m)+Abs(II*60.d0) If(Iph1(m).le.0.d0) Goto 333 Goto 360

333 II = Iph1(m)/60.d0-1

Id1(m) = Id1(m)+II Iph1(m)= Iph1(m)+Abs(II*60.d0) Goto 360

330 II = Giay1(m)/60.d0

Iph1(m) = Iph1(m)+II Giay1(m)= Giay1(m)-II*60.d0 If(Iph1(m).ge.60) Goto 331 Goto 360

331 II = Iph1(m)/60.d0

Id1(m) = Id1(m)+II Iph1(m)= Iph1(m)-II*60.d0 Goto 360

360 Write (4,313) M,Khd(Idfv(M)),Khd(Icfv(M))

* ,Id(m), Iph(m) , Giay(m), V, Id1(m), Iph1(m), Giay1(m) 313 Format ( 10x,'|', I2, ' |', A7, ' ', A7, ' |', I4, I3,

* F6.2, '|', F8.2,4X,'|', I4, I3, F6.2, '|' )

310 Continue

Write(4, 390)

390 Format(64('='))

PVV=Pvv1+Pvv2+Pvv3 Goto 1939

1222 PVV=Pvv1+Pvv2 1939 SSDV=dsqrt(PVV/(Ngoc+Ncanh+Nfv-2*Ndi+3))

Do 1989 K3=1,Ndi X(K3)=X(K3)+RLV(K3*2-1) Y(K3)=Y(K3)+RLV(K3*2)

1989 Continue 1889 Write(4, 1701) 1701 Format(//15x, 'V.KET QUA TOA DO DIEM SAU BINH SAI '/

X(m) | Y(m) |Mx(cm)|'

* 15x, '==================================== '// *10x,91('=')/ *10x,'| S | TEN | TOA DO | SAI SO VI' *' TRI DIEM | Elip sai so |'/ *10x,'| T | |-------------------------|----------' *'----------|------------------------------|'/ *10x,'| T | DIEM | *'My(cm)|Md(cm)| E | F | goc dinh huong |'/ *10x,'|---|-------|------------|------------|------|' *'------|------|------------------------------|')

Do 1710 I=1,Ndi Kx =(I*2-1)*(I*2-2)/2+I*2-1 Ky =(I*2)*(I*2-1)/2+I*2 Kxy=Ky-1 Qx =PTC(Kx) Qy =PTC(Ky) Qxy=PTC(Kxy)

Cao B¸ H¹

-76 -

Líp Tr¾c ®ÞaB-K48

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

SSx=100.d0*SSDV*Dsqrt(ABS(Qx)) SSy=100.d0*SSDV*Dsqrt(ABS(Qy)) SSd(I)=Dsqrt(SSx*SSx+SSy*SSy)

ZM(I)=Qx-Qy ZN(I)=2*Qxy ZZ=Qx+Qy ZR=Dsqrt(ZM(I)*ZM(I)+ZN(I)*ZN(I)) E(I)=SSDV*Dsqrt((ZZ+ZR)/2) F(I)=SSDV*Dsqrt((ZZ-ZR)/2) E1=1000.d0*E(I) F1=1000.d0*F(I) Ph(I)=dMod(dAtan2(ZN(I),ZM(I))+Pi2,Pi2) If(Ph(I).Lt.0.d0) Ph(I)=Ph(I)+Pi2 If(Ph(I).GT.Pi) Ph(I)=Ph(I)-Pi Ph1=Ph(I)

Call Drado(Ph1,Id,Iph,giay,Ro)

Write (4, 1711) I,Khd(I),X(I),Y(I),SSx,SSy,SSd(I),E1,F1,Id(I)

*,Iph(I)

1711 Format (10x,'|', I2,' |' , A7,'|', F12.3,'|', F12.3, '| ',

*F4.2, ' | ', F4.2, ' | ', F4.2, ' |',F5.2,' |',F5.2,' | ',I4,' *| ',I3,'

|')

1710 Continue

Write(4, 1712) 1712 Format(10x,91('='))

Do 1020 M=1, Ncanh I=Kd(M) J=Kc(M) Dx1= X(J)-X(I) Dy1= Y(J)-Y(I) Ds(m)= Dsqrt(Dx1**2+Dy1**2) Do 1021 L=1,Ian HV(L)= 0.d0

1021 Continue

HV(I*2-1)= -Dx1/Ds(m) HV(I*2) = -Dy1/Ds(m) HV(J*2-1)= Dx1/Ds(m) HV(J*2) = Dy1/Ds(m) QF= 0.d0 Call Dhts(Ian, QF) Sm(m)= SSDV*Dsqrt(ABS(QF)) Ktt(m)=(Ds(m)/Sm(m)) Ktt(m)=(Ktt(m)/1000.d0) Ktt(m)=Ktt(m)*1000.d0

1020 Continue

KI=1000000000 Do 80 I=1,Ncanh If(Ktt(I).GE.KI) Goto 80 KI=Ktt(I) Kj=Kd(I) Kn=Kc(I)

80 Continue

Do 760 m=1,Ncanh I=Kd(M) J=Kc(M) Dx1= X(J)-X(I) Dy1= Y(J)-Y(I) Ds(m)= Dsqrt(Dx1**2+Dy1**2) Do 1028 L=1,Ian HV(L)= 0.d0

Cao B¸ H¹

-77 -

Líp Tr¾c ®ÞaB-K48

§å ¸n tèt nghiÖp

Khoa Tr¾c ®Þa

1028 Continue

HV(I*2-1)= Ro*dy1/(Ds(m)**2) HV(I*2) = -Ro*dx1/(Ds(m)**2) HV(J*2-1)= -Ro*dy1/(Ds(m)**2) HV(J*2) = Ro*dx1/(Ds(m)**2) QF=0.d0 Call Dhts(Ian,QF) Sa(m)=SSDV*Dsqrt(ABS(QF))

760 Continue

ss=0.d0 Do 341 I=1,Ncanh If(Sa(I).LE.ss) Goto 341 ss=Sa(I) Ko=Kd(I) Kz=Kc(I)

341 Continue

Sd=0.d0 Do 342 I=1,Ndi If(SSd(I).LE.Sd) Goto 342 Sd=SSd(I) Km=I 342 Continue

Write(4,406)

406 Format(//15x,'VI. CAC YEU TO TUONG HO CUA LUOI'/

|Ma(")|'

* 15x,'================================'// *10x,82('=')/ *10x,'| No | Ten canh | Chieu dai | Phuong vi *' Ms(m)| Ms/S | Mth |'/ *10x,'|----|--------------|-----------|-------------|-----|' *'------|--------------|------|')

Do 400 M=1,Ncanh I=Kd(m) J=Kc(m) DX1=X(J)-X(I) DY1=Y(J)-Y(I) S(m)=dsqrt(DX1**2+DY1**2) tu=(S(m)*Sa(m))/Ro Sth(m)=dsqrt(Sm(m)*Sm(m)+Tu**2) afa=dMod(dAtan2(DY1,DX1)+Pi2,Pi2) If(afa.Lt.0.d0) afa=afa+Pi2 Call Drado (afa,Id,Iph,giay,Ro) Write(4,405) M,Khd(Kd(m)),Khd(Kc(m)),S(m),Id(m),Iph(m),giay(m),

*Sa(m),Sm(m),Ktt(m),Sth(m)

405 Format(10x,'|',I3,' |',A7,A7,'|',F11.3,'|',I4,I3,F6.2,'|',

*F5.2,'|',F6.3,'|',' 1:',I8,' |',F6.3,'|')

400 Continue

Write(4,407) 407 Format(10x,82('=')) Write(4, 2001)

2001 Format(/10x,'VII.KET LUAN'/ * 10x,'============')

Write(4,1027) SSDV

1027 Format(/15x,

* '1. Sai so trung phuong trong so don vi mo =', * F6.2, ' " ')

Write (4,348) Khd(Ko),Khd(Kz),ss

348 Format(15x,'2. Phuong vi yeu nhat ',

* A7,'- ',A7,' ma =',F6.2,' " ')

Write (4,1119) Khd(Kj),Khd(Kn),KI 1119 Format(15x,'3. Canh yeu nhat ',

Cao B¸ H¹

-78 -

Líp Tr¾c ®ÞaB-K48

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

*A7,'- ',A7,'ms/S = 1/',I6)

Write(4,453) Khd(Km),Sd

453 Format(15x,'4. Diem yeu nhat ',A7,'

M =',

* F6.2,'(cm)') Write(4,566)

566 Format(///40x,' Nguoi thuc hien: Cao Ba Ha '/ * 40x,' Lop : Trac dia B - K48'/ * 40x,' TRUONG DAI HOC MO - DIA CHAT '/)

0'/'SECTION'/' 2'/'ENTITIES')

162

Write(6,69) Format(' Do 83 I=1,Ncanh Write(6,93) Y(Kd(I)),X(Kd(I)),Y(Kc(I)),X(Kc(I)) Format( *' 0'/'LINE'/' 8'/'CANH'/' 62'/'131'/' 10'/f18.3/' 20'/f18.3/ *' 30'/'0.0'/' 11'/f18.3/' 21'/f18.3/' 31'/'0.0') Continue Do 131 I=1,Ngoc Write(6,162) Y(It(I)),X(It(I)),Y(Ig(I)),X(Ig(I)) Format( *' 0'/'LINE'/' 8'/'CANH'/' 62'/'131'/' 10'/f18.3/' 20'/f18.3/ *' 30'/'0.0'/' 11'/f18.3/' 21'/f18.3/' 31'/'0.0')

131 Continue

137

Do 138 I=1,Ngoc Write(6,137) Y(Ig(I)),X(Ig(I)),Y(Ip(I)),X(Ip(I)) Format( *' 0'/'LINE'/' 8'/'CANH'/' 62'/'131'/' 10'/f18.3/' 20'/f18.3/ *' 30'/'0.0'/' 11'/f18.3/' 21'/f18.3/' 31'/'0.0')

138 Continue

821

839

721

Do 839 I=(Nxd+1),Ndi Write(6,821) Y(I),X(I),Cch,Khd(I) Format(' 0'/'TEXT'/' 8'/'TEN_DIEM'/' 62'/'30'/' 10'/F18.3/ *' 20'/F18.3/' 30'/'0.0'/' 40'/F8.1/' 1'/A7/' 41'/'0.7'/ *' 7'/'STANDARD') Continue Do 739 k=1,Nxd Write(6,721) Y(k),X(k),Cch,Khd(k) Format(' 0'/'TEXT'/' 8'/'TEN_DIEM'/' 62'/'50'/' 10'/F18.3/ *' 20'/F18.3/' 30'/'0.0'/' 40'/F8.1/' 1'/A7/' 41'/'0.7'/ *' 7'/'STANDARD') Continue

739

957

Cd=10.d0 Do 961 I=1,Ncanh I1=Kd(I) J1=Kc(I) dx11 =X(J1)-X(I1) dy11 =Y(J1)-Y(I1) afS = dMod(dAtan2(dy11,dx11)+Pi2,Pi2) If(afS.LT.0) afS = afS + Pi2 Xg(I)=(X(I1)+X(J1))/2 Yg(I)=(Y(I1)+Y(J1))/2 Xq1=Xg(I)+cd*dcos(afS+Pi/2) Yq1=Yg(I)+cd*dsin(afS+Pi/2) Xq2=Xg(I)+cd*dcos(afS+(3*Pi)/2) Yq2=Yg(I)+cd*dsin(afS+(3*Pi)/2) Write(6,957) Yq1,Xq1,Yq2,Xq2 Format( *' 0'/'LINE'/' 8'/'KH-CANHDO'/' 62'/'120'/' 10'/f14.3/ *' 20'/f14.3/' 30'/'0.0'/' 11'/f14.3/' 21'/f14.3/' 31'/'0.0') Continue

961

Cao B¸ H¹

-79 -

Líp Tr¾c ®ÞaB-K48

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

849

847

dl =25.d0 Do 847 I=1,Ngoc dxt=X(It(I))-X(Ig(I)) dyt=Y(It(I))-Y(Ig(I)) dxp=X(Ip(I))-X(Ig(I)) dyp=Y(Ip(I))-Y(Ig(I)) afat= dMod(dAtan2(dxt,dyt)+Pi2,Pi2) afap= dMod(dAtan2(dxp,dyp)+Pi2,Pi2) afat= afat*180.d0/pi afap= afap*180.d0/pi Write(6,849) Y(Ig(I)),X(Ig(I)),dl,afap,afat Format(' 0'/'ARC'/' 8'/'KH-GOC'/' 62'/'6'/' 10'/F18.3/' 20' * /F18.3/' 30'/' 0.0'/' 40'/F8.1/' 50'/F11.6/' 51'/F11.6) Continue Do 654 I=1,Ndi Write(6,201) Y(I),X(I),bk

201 FORMAT(' 0'/'CIRCLE'/' 8'/'VT-diem'/' 62'/'13'/' 10'/F12.3/

*' 20'/F12.3/' 30'/'0.0'/' 40'/F10.3) Continue

654

767

768

769

770

Do 766 I=1,Ndi Yf=F(I)/50 Do 767 K=2,50 K1=K-1 Ye(K)=-K1*Yf Ca1=E(I)*dsqrt(F(I)*F(I)-Ye(K)*Ye(K)) Xe(K)=Ca1/F(I) Se(K)=dsqrt(Xe(K)*Xe(K)+Ye(K)*Ye(K)) Continue Do 768 J=52,100 J1=J-51 Ye(J)=-(F(I)-J1*Yf) Ca2=E(I)*dsqrt(F(I)*F(I)-Ye(J)*Ye(J)) Xe(J)=-Ca2/F(I) Se(J)=dsqrt(Xe(J)*Xe(J)+Ye(J)*Ye(J)) Continue Do 769 J2=102,150 J3=J2-101 Ye(J2)=J3*Yf Ca3=E(I)*dsqrt(F(I)*F(I)-Ye(J2)*Ye(J2)) Xe(J2)=-Ca3/F(I) Se(J2)=dsqrt(Xe(J2)*Xe(J2)+Ye(J2)*Ye(J2)) Continue Do 770 K2=152,200 K3=K2-152 Ye(K2)=(F(I)-K3*Yf) Ca4=E(I)*dsqrt(F(I)*F(I)-Ye(K2)*Ye(K2)) Xe(K2)=Ca4/F(I) Se(K2)=dsqrt(Xe(K2)*Xe(K2)+Ye(K2)*Ye(K2)) Continue Xe(1) = E(I) Ye(1) = 0.d0 Se(1) = E(I) Xe(51)= 0.d0 Ye(51)=-F(I) Se(51)= F(I) Xe(101)=-E(I) Ye(101)= 0.d0 Se(101)= E(I) Xe(151)= 0.d0

Cao B¸ H¹

-80 -

Líp Tr¾c ®ÞaB-K48

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

771

773

772 766

209

Ye(151)= F(I) Se(151)= F(I) Aft=dmod(dAtan2(Ye(1),Xe(1))+Pi2,Pi2) Do 771 Im=1,200 Afp=dmod(dAtan2(Ye(Im),Xe(Im))+Pi2,Pi2) Beta(Im)= Afp-Aft If(Beta(Im).Lt.0.d0) Beta(Im)=Beta(Im)+Pi2 Se(Im)=15000.d0*Se(Im) Af1=Ph(I)+Beta(Im) X2(Im)=X(I)+Se(Im)*dcos(Af1) Y2(Im)=Y(I)+Se(Im)*dsin(Af1) Continue Do 772 I6=1,200 X2(201)=X2(1) Y2(201)=Y2(1) Write(6,773) Y2(I6),X2(I6),Y2(I6+1),X2(I6+1) Format( *' 0'/'LINE'/' 8'/'ELIP-SAISO'/' 62'/'10'/' 10'/f14.3/ *' 20'/f14.3/' 30'/'0.0'/' 11'/f14.3/' 21'/f14.3/' 31'/'0.0') Continue Continue Write(6,209) Format(' 0'/'ENDSEC'/' 0'/'EOF') Close(6) Stop End

$debug $large c Binh sai luoi do cao thi cong c Ho va ten : Cao Ba Ha c Lop : Trac dia BK48

Implicit Real *8(a-h, o-z) Character ff*50, Tenct*50, Tr*7 Character Khd(200)*8 Dimension H(200),hh(200),S(200),Kd(500),Kc(500),RLV(100),RH(100) Common /v1/ HV(200), PTC(5000)

Write (*,*) 'Nhap ten file so lieu : ' Read (*,'(a)') ff Open (1, file=ff, status='old') Write (*,*) 'Nhap ten file ket qua : ' Read (*,'(a)') ff Open (4, file=ff, status='new') Read (1,'(a)') Tenct Read (1,*) Ng, Nxd, Ncc,Gh a= -10000000000.d0 Ndi= (Ng+Nxd) Do 1 I= 1, Ndi H(I)= a Continue Read(1,89) (Khd(m),m=1,Ndi) Format(10A6) Read(1,*) (H(k),K=(Nxd+1),Ndi) Do 3 I= 1, Ncc Read (1,*) Kd(I), Kc(I), hh(I), S(I) Continue Write (4,5) Ng, Nxd, Ncc Format (//15x, 'KET QUA BINH SAI LUOI DO CAO '/

* 15x, '===========* * *============'// * 15x, 'I.SO LIEU KHOI TINH'/ * 15x, '==================='/ * 15x, 'So diem do cao goc : ',I3/ * 15x, 'So diem can xac dinh : ',I3/

Cao B¸ H¹

-81 -

Líp Tr¾c ®ÞaB-K48

2. Ch¬ng tr×nh b×nh sai líi ®é cao thi c«ng

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

* 15x, 'So luong chenh cao do : ',I3// )

12 13

20 6

LT= 0 Do 10 I= 1, Ncc If (H(Kd(I)).ne.a.and.H(Kc(I)).eq.a) Goto 11 If (H(Kd(I)).eq.a.and.H(Kc(I)).ne.a) Goto 12 Goto 10 H(Kc(I))= H(Kd(I))+hh(I) Goto 13 H(Kd(I))= H(Kc(I))-hh(I) LT= LT+1 If (LT.eq.Nxd) Goto 20 Continue Goto 14 Write (4,6) 'II. DO CAO DIEM DINH VI' Format (15x, A23/

* 15X, 23('=')// * 10x, 44('-')/ * 10x, '| S | TEN | DO CAO |'/ * 10x, '| T | |----------------------------|'/ * 10x, '| T | DIEM | H(mm) Ghi chu |'/ * 10x, '|------------------------------------------|')

22 21

199

101

100

66 65

71 70

Do 21 J= (Nxd+1), Ndi Write (4,22) J, Khd(J), H(J) Format (10x,'|', I3,' |', A7,'|', F9.2,' |',14X,'|') Continue Write(4,23) Format(10x,44('-')) Ian=Ndi KL=(Ian-1)*Ian/2+Ian Ms=Ian*(Ian+1)/2 Do 199 K=1,Ms PTC(K)=0.d0 Continue Do 100 M= 1, Ncc Do 101 K= 1, (Ian+1) HV(K)=0d0 continue I= Kd(M) J= Kc(M) HV(I)= -1d0 HV(J)= 1d0 HV(Ian+1)= H(J)-H(I)-hh(M) P= 1/S(M) Call dPTC (Ian, P) Continue Do 65 I=(Nxd+1),Ian Do 66 J=I,Ian K=J*(J-1)/2+I PTC(K)=PTC(K)+1.d0 Continue Continue Ls=Ian-1 Call DTDNG(Ls) Call DNDAO(Ian) Do 70 I=1,Ian Do 71 J=I,Ian L1=J*(J-1)/2+I PTC(L1)=PTC(L1)-1.d0/(Ng*1.d0)**2 Continue Continue Do 80 I1=1,Ian RLV(I1)=0.d0 Continue Do 82 I=1,Ian Do 83 J=1,Ian If(J.GT.I) Goto 84 K=(I-1)*I/2+J

Cao B¸ H¹

-82 -

Líp Tr¾c ®ÞaB-K48

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

84 85 83 82

Goto 85 K=J*(J-1)/2+I RLV(I)=RLV(I)-PTC(K)*PTC(Ms+J) Continue Continue Write (4,60) 'III. DO LECH CAO DO CUA CAC DIEM DINH VI'

60 Format (12x, A40/

* 12X, 40('=')// * 10x, 44('-')/ * 10x, '| S | TEN | DO lech |'/ * 10x, '| T | |----------------------------|'/ * 10x, '| T | DIEM | dH(mm) Ghi chu |'/ * 10x, '|------------------------------------------|')

Write (4, 711) (K,Khd(K),RLV(K),K=(nxd+1),Ndi)

711 Format (10x,'|', I3,' |', A7,'|', F9.2,' |',14X,'|')

Write(4,33)

33 Format(10x,44('-'))

Write (4,7) 'IV.KET QUA TRI DO SAU BINH SAI'

7 Format (//15x, A30/

* |'/ *'| THU| ------------- | CAO DO | CHINH | BINH SAI | * |'/ *'| TU | DAU – CUOI | (mm) | (mm) | (mm) |(mm *)|'/ * 67('-')) PVV= 0.d0 Do 500 m= 1, ncc Do 501 K= 1, (Ian+1) HV(K)=0.d0

501 continue I= Kd(M) J= Kc(M) HV(I)= -1d0 HV(J)= 1d0 QF=0.d0 Call Dhts(Ian,QF) HV(Ian+1)= H(J)-H(I)-hh(M) P= 1/S(M) V= 0.d0 Do 502 K=1, Ian V= V+HV(K)*RLV(K)

502 Continue

V= V+HV(Ian+1) PVV= PVV+ V*V*P PVV= abs(PVV) SSDV= dSQRT(PVV/(Ncc-Ndi+1)) Sa=SSDV*Dsqrt(ABS(QF)) hhbs= hh(m)+V Write(4, 503) m, Khd(I), Khd(J), hh(m), V, hhbs, sa

503 Format ('|', I3, ' | ', A6,'- ',A6, '|'

* F10.2, 5X, '|', F7.2, '| ', F9.2, 4X,'|', F4.2, '|')

500 Continue

Write(4,504)

504 Format(67('-'))

Write (4, 259) 'V.DO CAO DIEM SAU BINH SAI'

259 Format (//15x, A28/

* 17x, 26('=')// * 57('=')/ *'| S | TEN | DO CAO | SAI SO | | '/ *'| T | | ------------------------ | GHI CHU | '/ *'| T | DIEM | (mm) | (mm) | '/ *'--------------------------------------------------------| ')

Cao B¸ H¹

-83 -

Líp Tr¾c ®ÞaB-K48

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

Do 400 I= 1, Ian K= I*(I-1)/2 + I QH= ptc(k) SSH= SSDV*dSqrt(ABS(QH)) HBS= H(I)+RLV(I) Write (4, 401) I, Khd(I), HBS, SSH

401 Format ('|', I3, ' | ', A7, '|', F10.2, ' | ', F7.2,' |' * 12x, '|')

400 Continue

402

Write(4,402) Format(57('-')) Write (4,505) ssdv

505 Format (//15x, 'DO CHINH XAC DO DAC'/

* 15x, '-------------------'// * 15x,'Sai so trung phuong trong so don vi:',F5.2, 'mm'// * ' GHI CHU : '/ * 10x, '- Nguoi tinh : Cao Ba Ha'/ * 10x, '- Lop trac dia BK48'/ * 10x, '- Truong dai hoc Mo Dia chat'/)

Stop End

$debug $large c CHUONG TRINH TINH CHUYEN TU XY SANG BL c Ho va ten :Cao Ba Ha c Lop : Trac dia B-K48

Implicit Real *8(a-h, o-z) Character ff*50,Tenct*100, td(100)*100 Dimension X(1000),Y(1000)

b1= 1.d0 Pi= 4.d0*dAtan(b1) Pi2= 2.d0*Pi Ro= 3600.d0*180.d0/Pi Write (*,'(a\)') ' Nhap ten file so lieu : ' Read (*,'(a)') ff Open (1, file=ff, status='old') Write (*,'(a\)') ' Nhap ten file ket qua : ' Read (*,'(a)') ff Open (4, file=ff, status='new')

Read (1,'(a)') Tenct Read(1,*) Nd,a,b2,dMo Read(1,50) (td(I),I=1,Nd) Format(10A7) Read(1,*) Id1,Iph1,G1 GL0=(Id1*3600.d0+Iph1*60.d0+G1)/Ro Read (1,*) I0do, I0ph, g0 dl0= (I0do*3600.d0 + I0ph*60.d0 +g0)/Ro Do 1 I=1,Nd Read(1,*) I,X(I),Y(I) Continue Gh=0.0000000000000001d0 a22=a*a b22=b2*b2 e2=(a22-b22)/a22 ep2=(a22-b22)/b22 c=a/dsqrt(1-e2) Ao1=1.d0-3.d0*ep2/4.d0+ 45.d0*(ep2**2)/64.d0 Ao2=-175.d0*(ep2**3)/256.d0+ 11025.d0*(ep2**4)/16384.d0

Cao B¸ H¹

-84 -

Líp Tr¾c ®ÞaB-K48

3. Ch¬ng tr×nh tÝnh chuyÓn to¹ ®é

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

Ao=Ao1+Ao2 A2=Ao-1.d0 A4=15.d0*(ep2**2)/32.d0-175.d0*(ep2**3)/384.d0+3675.d0*(ep2**4) */8192.d0 A6=-35.d0*(ep2**3)/96.d0+735.d0*(ep2**4)/2048.d0 A8=315.d0*(ep2**4)/1024.d0 Write(4,6) tenct Format(///32x,'KET QUA TINH CHUYEN TOA DO PHANG'/ *36x,'TRONG CUNG HE QUY CHIEU'// *27x,A100/ *32x,'--------------------------------'/ *113('=')/ *'| | | TOA DO TRONG HE CU |' *' TOA DO TRONG HE MOI | TOA DO TRAC DIA |'/ *'| STT | TEN DIEM |-------------------------------|' *'--------------------------------------------------------------|'/ *'| | | X(m) | Y(m) |' *' X(m) | Y(m) | B | L |'/ *'|-----|----------|---------------|---------------|' *'---------------|---------------|---------------|--------------|')

Do 2 I=1,Nd Y(I)=Y(I)-500000.d0 Bo1=20.d0 t=dcos(Bo1) t1=dsin(Bo1) t2=t*t t4=t2**2 t6=t2**3 Bo=(X(I)/(dMo*c)-(A2+A4*t2+A6*t4+A8*t6)*t*t1)/Ao ep1=ABS(Bo-Bo1) If(ep1.LE.Gh) Goto 3 Bo1=Bo Goto 4 to=dtan(Bo) tN=a/dsqrt(1.d0-e2*dsin(Bo)*dsin(Bo)) tM=(1.d0-e2)*tN/(1.d0-e2*dsin(Bo)*dsin(Bo)) P=tN/tM y2=Y(I)*Y(I) y3=Y(I)*Y(I)*Y(I) y4=y2*y2 y5=y2*y3 y6=y2**3 y7=y3*y4 y8=y2**4 dM2=dMo**2 dM3=dMo**3 dM4=dMo**4 dM5=dMo**5 dM6=dMo**6 dM7=dMo**7 dM8=dMo**8 tN3=tN**3 tN5=tN**5 tN7=tN**7 to2=to**2 to4=to**4 to6=to**6 P2=P**2 P3=P**3 P4=P**4

Cao B¸ H¹

-85 -

Líp Tr¾c ®ÞaB-K48

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

R1=(to*y2)/(2.d0*dM2*tM*tN) R2=(to*y4)/(24.d0*dM4*tM*tN3) R21=(-4.d0*P2+9.d0*P*(1.d0-to2)+12.d0*to2) R3=(to*y6)/(720.d0*dM6*tM*tN5) R31=8.d0*P4*(11.d0-24.d0*to2)-12.d0*P*P2*(21.d0-71.d0*to2) R32=15.d0*P2*(15.d0-98.d0*to2+15.d0*to4)+180.d0*P*(5.d0*to2-

*3.d0*to4)+360.d0*to4 R4=(to*y8)/(40320.d0*dM8*tM*tN7) R41=(1385.d0+3633.d0*to2+4095.d0*to4+1575.d0*to6) GB=Bo-R1+R2*R21-R3*(R31+R32)+R4*R41 SB=1.d0/dcos(Bo) q1=Y(I)/(dMo*tN) q2=y3*(P+2.d0*to2)/(6.d0*dM3*tN3) q3=y5/(120.d0*dM5*tN5) q31=(-4.d0*P3*(1.d0-6.d0*to2)+P2*(9.d0-68.d0*to2)+72.d0*P*to2 *+24.d0*to4) q4=y7/(5040.d0*dM7*tN7) q41=(61.d0+662.d0*to2+1320.d0*to4+720.d0*to6) dl=sb*(q1-q2+q3*q31-q4*q41) GL=GL0+dl e=dsqrt((a22-b22)/a22) dl1=Gl-dl0 dt=dtan(GB) fi=(1.d0-e**2*(dsin(GB))**2)/(1.d0-e**2) b0=1.d0+0.75d0*e**2+(45.d0/64.d0)*e**4+(175.d0/256.d0)*e**6 b222=0.75d0*e**2+(15.d0/16.d0)*e**4+(525.d0/512.d0)*e**6 b4=(15.d0/64.d0)*e**4+(105.d0/256.d0)*e**6 b6=(35.d0/512.d0)*e**6 X0=a*(1.d0-e**2)*(b0*GB-(b222/2.d0)*dsin(2.d0*GB)+(b4/4.d0)* *dsin(4.d0*GB)-(b6/6.d0)*dsin(6.d0*GB)) dN=a/dsqrt(1.d0-e**2*(dsin(GB))**2) dc=dcos(GB) ds=dsin(GB)

dx=dmo*(X0+dN*ds*dc*dl1**2/2.d0+dN*ds*dc**3*(4.d0*fi**2+fi-

*dt**2)*dl1**4/24.d0+dN*ds*dc**5.d0*(8*fi**4*(11.d0-24.d0*dt**2) *-28.d0*fi**3*(1.d0-6*dt**2)+fi**2*(1.d0-32.d0*dt**2)-fi*(2.d0* *dt**2)+dt**4)*dl1**6/720.d0+dN*ds*dc**7*(1385.d0-3111.d0*dt**2+ *543.d0*dt**4-dt**6)*dl1**8/40320.d0)

dy=dmo*(dN*dl1*dc+dN*dc**3*(fi-dt**2)*dl1**3/6.d0+dN*dc**5* *(4.d0*fi**3*(1.d0-6.d0*dt**2)+fi**2*(1+8.d0*dt**2)-2.d0*fi* *dt**2+dt**4)*dl1**5/120.d0+dN*dc**7*(61.d0-479.d0*dt**2+179.d0* *dt**4-dt**6)*dl1**7/5040.d0) dy=dy+500000.d0 Y(I)=Y(I)+500000.d0 Call Drado(GB,Id,Iph,g,Ro) Call Drado(GL,Id2,Iph2,g2,Ro) Write (4,7) I,td(I),x(I),Y(I), dx, dy,Id,Iph,g,Id2,Iph2,g2

7 Format ( '|',I5,'| ',A7,' |',F15.3,'|',F15.3,'|',F15.3,'|',F15.3,

*'|',I3 , I3 , F8.4 ,' |', I3 , I3 , F8.4,'|') Continue Write(4,8) Format (113('=')) Write(4,16)

16 Format(///60x,' Nguoi thuc hien: Cao Ba Ha '/ * 60x,' Lop : Trac dia B - K48'/ * 60x,' TRUONG DAI HOC MO - DIA CHAT '/)

Stop

End

Cao B¸ H¹

-86 -

Líp Tr¾c ®ÞaB-K48

Khoa Tr¾c ®Þa

§å ¸n tèt nghiÖp

tµi liÖu tham kh¶o

[1]. GS.TSKH. Hoµng Ngäc Hµ - TS. Tr¬ng Quang HiÕu (1999), C¬ së to¸n