1
1. Hình chóp tam giác
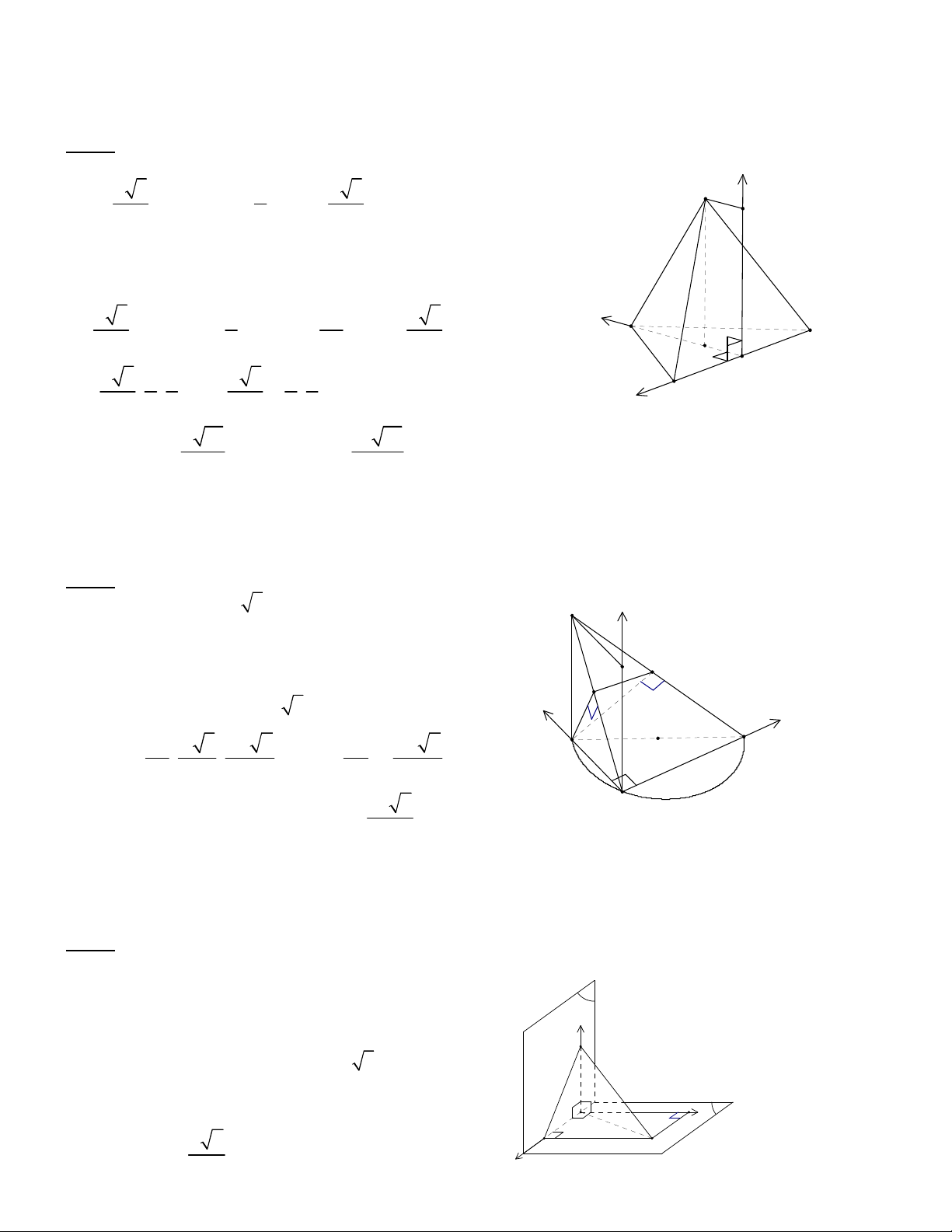
Bài 1. (Trích  thi tuyn sinh H Khi A nm 2002). Cho hình chóp tam giác u
.
S ABC
có  dài cnh
AB a
=
. Gi M, N ln lt là trung im ca các cnh SB, SC. Tính theo a din tích ca tam giác AMN,
bit rng mt phng (AMN) vuông góc vi mt phng (SBC).
Gi ý:
Gi O là trung im BC, G là trng tâm tam giác ABC, ta có
3 3
2 2 6
a a a
OA OB OC OG= = = =
t
0.
SG z
= >
Chn h trc ta
Oxyz
sao cho tia
Ox
cha A,
tia
Oy
cha B và tia
Oz
nm trên ng thng qua O và song
song vi SG (xem hình v). Khi ó
3 3
;0;0 , 0; ;0 , 0; ;0 , ;0; .
2 2 2 6
a a a a
A B C S z
−
3 3
; ; , ; ; .
12 4 2 12 4 2
a a z a a z
M N
−
Tính c
15
.
6
a
z= Suy ra
2
10
.
16
AMN
a
S=
x
y
z
GO
S
A
B
C
Bài 2. (Trích  d b 1 – H Khi B nm 2007). Trong na mt phng (P) cho ng tròn ng kính AB
và im C trên na ng tròn ó sao cho
AC R
=
. Trên ng thng vuông góc vi (P) ti A ly im S
sao cho góc gia hai mt phng (SAB) và (SBC) bng
60
o
. Gi H, K ln lt là hình chiu ca A trên SB,
SC. Chng minh rng tam giác AHK vuông và tính th tích khi chóp
. .
S ABC
Gi ý:
Ta có
, 3.
AC R BC R= = t
0.
SA z
= >
Chn h trc ta 
Oxyz
sao cho
,
O C
≡
tia
Ox
cha A,
tia
Oy
cha B và tia
Oz
nm trên ng thng qua O và
song song vi SA (xem hình v). Khi ó:
(
)
(
)
(
)
(
)
0;0;0 , ;0;0 , 0; 3;0 , ;0; .
C A R B R S R z
Khi ó tính
c
8 3 4 2
; ;
9 9 9
R R R
H
và
2 2 2
;0; .
3 3
R R
K
Th tích khi chóp
.
S ABC
là:
3
.
6
.
12
S ABC
R
V=
2R
xy
z
A
S
B
C
K
H
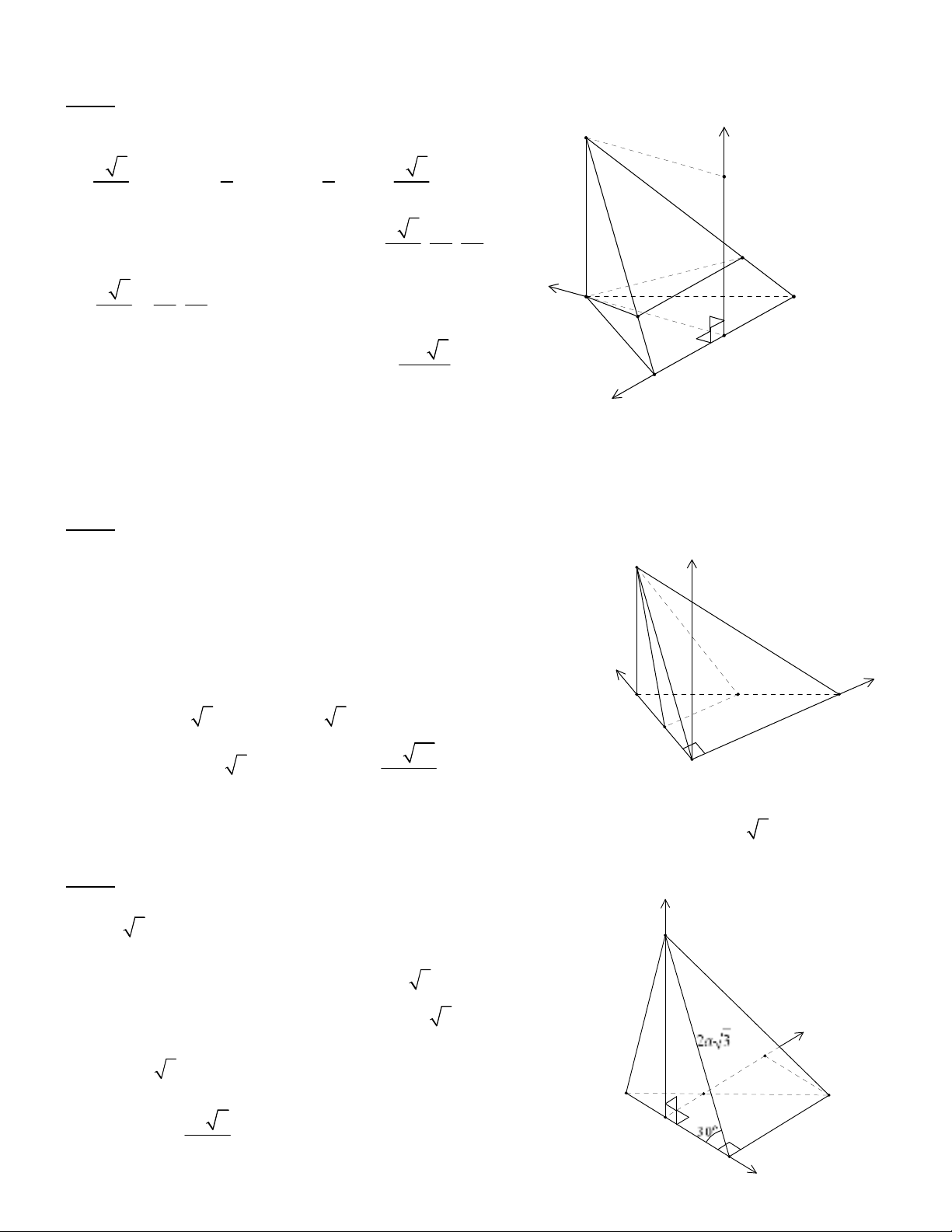
Bài 3. (Trích  tuyn sinh H Khi D nm 2003). Cho hai mt phng (P) và (Q) vuông góc vi nhau, có
giao tuyn là ng thng
∆
. Trên
∆
ly hai im A,B vi
AB a
=
. Trong mt phng (P) ly im C, trong
mt phng (Q) ly im D sao cho AC, BD cùng vuông góc vi
∆
và
.
AC BD AB a
= = =
Tính bán kính
mt cu ngoi tip t din ABCD và tính khong cách t A n mt phng (BCD) theo a.
Gi ý:
+ Chn h trc ta  Oxyz nh hình v, lúc ó
(
)
;0;0 , (0;0;0), ( ; ;0), (0;0; ).
A a B C a a D a
+ Mt cu ngoi tip t din ABCD có tâm
(
)
/ 2; / 2; / 2
I a a a và bán kính
3 / 2.
=R a
+ Mt phng (BCD) có phơng trình
0.
x y
− =
+ Khong cách t A n (BCD) là
( )
2
,( ) .
2
a
d A BCD =
P
Q
a
a
a
y
z
x
A
B
D
C
2
Bài 4. (Trích  tuyn sinh H Khi D nm 2006). Cho hình chóp tam giác S.ABC có áy ABC là tam giác
u cnh a,
2
SA a
=
và SA vuông góc vi mt phng (ABC). Gi M, N ln lt là hình chiu vuông góc
ca A trên các ng thng SB và SC. Tính th tích khi chóp A.BCNM.
Gi ý:
+ Gi O là trung im BC. Chn h trc ta  Oxyz nh
hình v, lúc ó
3 3
;0;0 , 0; ;0 , 0; ;0 , ;0;2 .
2 2 2 2
a a a a
A B C S a
−
+ Tìm c ta  các im M, N là
3 2 2
; ;
10 5 5
a a a
M
và
3 2 2
; ; .
10 5 5
a a a
N
−
+ Th tích khi chóp A.BCNM là
3
.
3 3
.
50
A BCNM
a
V=
a
2a
z
x
y
N
O
S
C
B
A
M
Bài 5. (Trích  tuyn sinh H Khi A nm 2011). Cho hình chóp S.ABC áy ABC là tam giác vuông cân
ti B,
2
AB BC a
= =
, hai mt phng (SAB) và (SAC) cùng vuông góc vi mt phng (ABC). Gi M là trung
im ca AB; mt phng qua SM và song song vi BC, c t AC ti N. Bit góc gia hai mt phng (SBC) và
(ABC) bng
60
o
. Tính th tích khi chóp S.BCNM và khong cách gia hai ng thng AB và SN theo a.
Gi ý:
+t
0.
SA z
= >
Chn h ta  Oxyz nh hình v, lúc ó:
(
)
(
)
(
)
2 ;0;0 , 0;0;0 , 0;2 ;0 ,
A a B C a
(
)
;0;0 , (2 ;0; ).
M a S a z
+ Tìm c im
(
)
; ;0 .
N a a
+ Vectơ pháp tuyn ca (SBC) là
(
)
;0; 2 .
SBC
n z a
= −
+Vectơ pháp tuyn ca (ABC) là
(
)
0;0;1 .
ABC
n=
+ T gi thit góc gia hai mt phng (SBC) và (ABC) bng
60
o
tìm c
(
)
2 3 2 ;0; 2 3 .
z a S a a=
+ Suy ra 3
3
SBCNM
V a= và
2 39
( , ) .
13
a
d AB SN =
z
y
xN
M
C
B
A
S
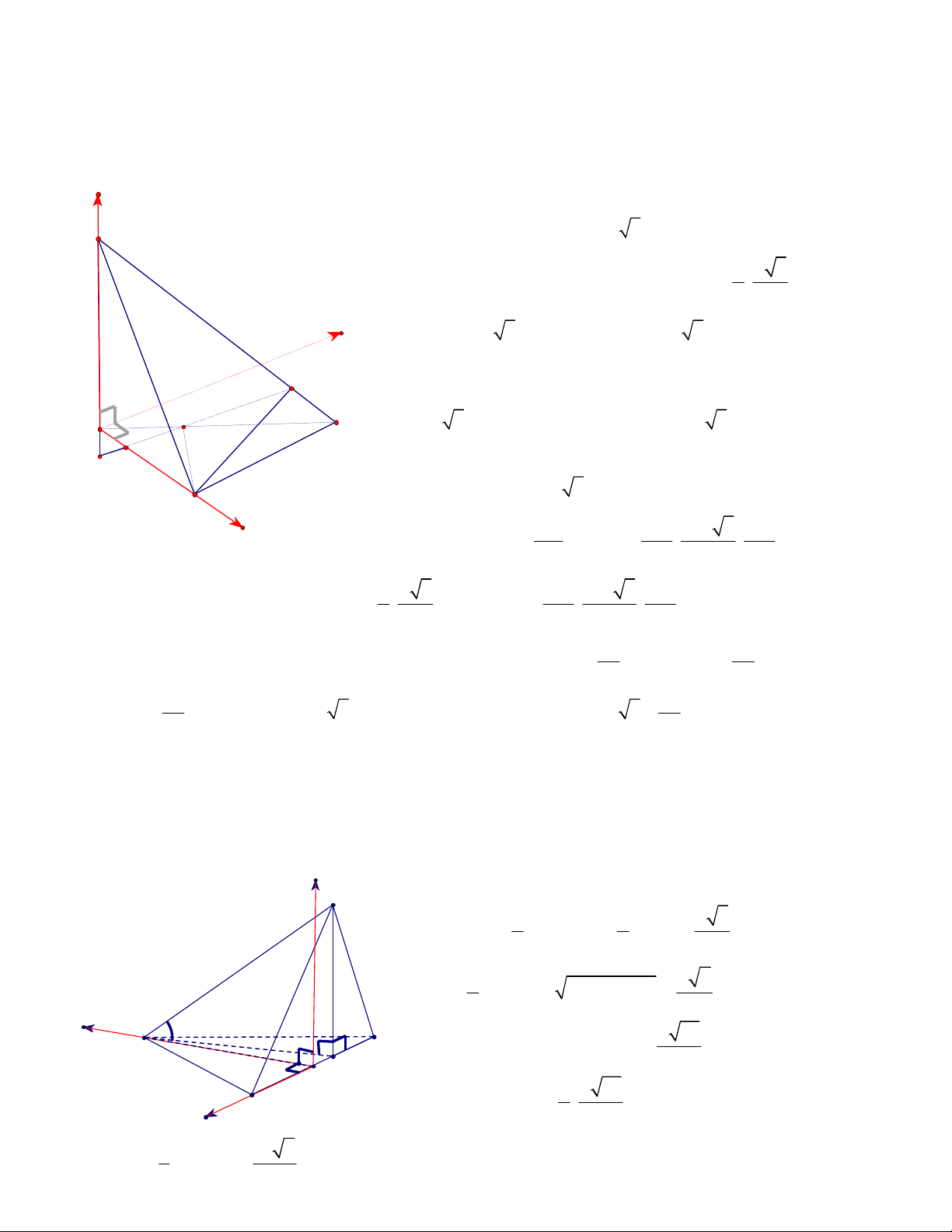
Bài 6. (Trích  tuyn sinh H Khi D nm 2011). Cho hình chóp S.ABC có áy ABC là tam giác vuông ti
B,
3 , 4
BA a BC a
= =
, mt phng (SBC) vuông góc vi mt phng (ABC). Bit
2 3
SB a
= và
30 .
o
SBC
=
Tính th tích khi chóp S.ABC và khong cách t im B n mt phng (SAC) theo a.
Gi ý:
+ K!
,
SO BC
⊥
khi ó
( )
SO ABC
⊥
. Tính c
3, 3 , .
SO a OB a OC a
= = =
+ Chn h ta  Oxyz nh hình v, lúc ó:
(
)
(
)
(
)
(
)
3 ;3 ;0 , 3 ;0;0 , ;0;0 , 0;0; 3 .
A a a B a C a S a−
+ Tính th tích khi chóp S.ABC là 3
.
2 3.
S ABC
V a=
+ Phơng trình mt phng (SAC) là:
3 4 3 3 0.
x y z a
− + + − =
+ Khong cách t im B n mt phng (SAC) là
( )
6 7
,( ) .
7
a
d B SAC =
4a 3a
z
y
x
S
A
B
C
O
3
Chuyên Lam Sn - Thanh Hóa: Cho t din ABCD có AD vuông góc vi mt phng (ABC), AD = 3a,
AB = 2a, AC = 4a,
 
=
. Gi H, K ln lt là hình chiu vuông góc ca B trên AC và CD. ng
thng HK c t ng thng AD ti E. Chng minh rng BE vuông góc vi CD và tính th tích khi t din
BCDE theo a.
Gii:




E
A
B
C
D
x
z
y
H
K
Chn h trc ta  Oxyz nh hình v vi A trùng vi gc ta
 O.
A(0;0;0), B(2a;0;0),
(
)

, D(0;0;3a)

 
= =
. Suy ra ta  ca
(
)


= −
suy ra
(
)

= −
là mt vecto ch"
phơng ca DC nên phơng trình ng thng DC là:
=
=
= −
. Vì K thuc DC nên
(
)
−.
Ta có
(
)

= − −


  = ⇔ =
. V#y
  
  
Vì E thuc trc Az nên E(0;0;z).

= −
;
  
  

=
Vì E, H, K thng hàng nên
 
cùng phơng, do ó suy ra
= − . V#y E(0;0;
−).


=
và
(
)


= −
nên

.

=
( )
 
+ + − =
V#y BE vuông góc vi CD.
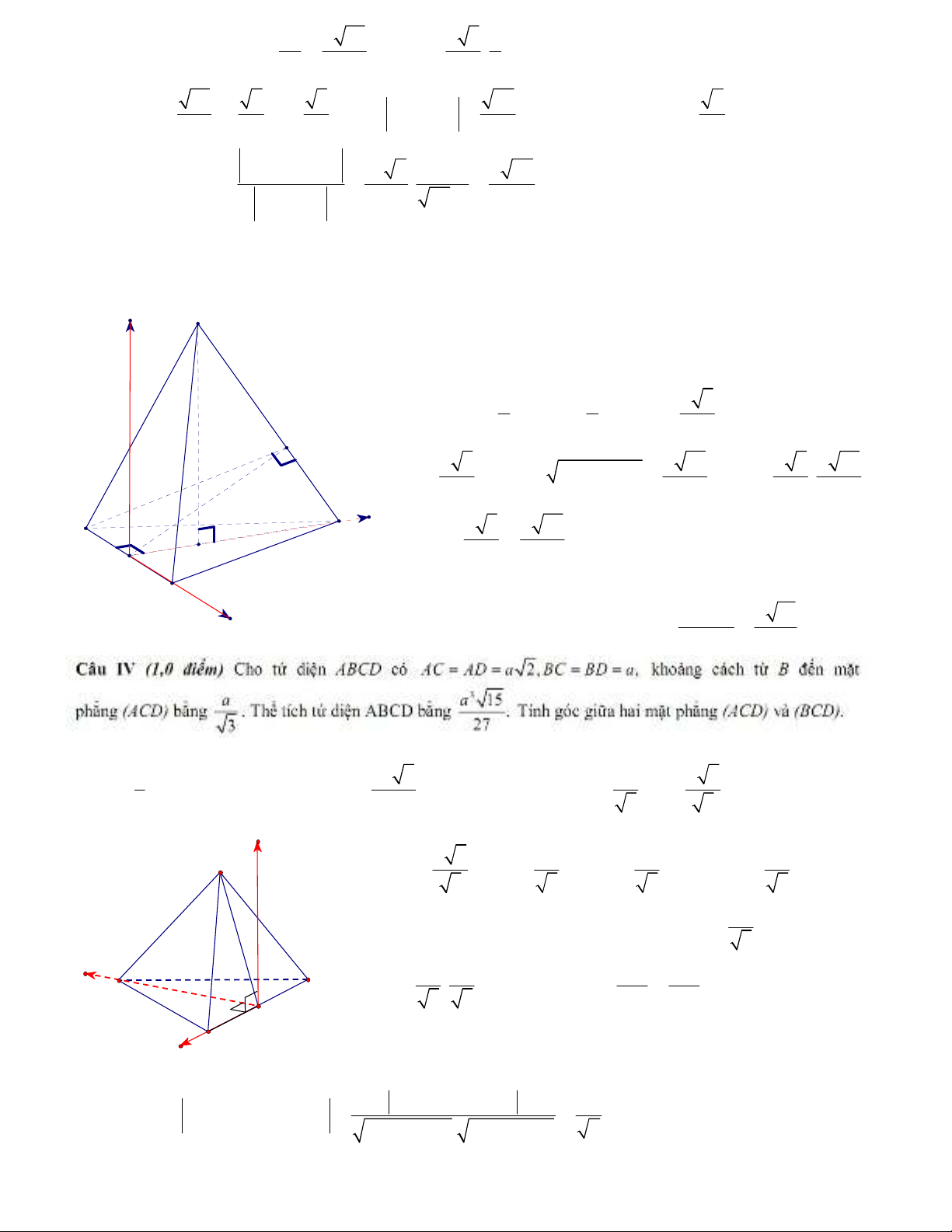
A12: Cho hình chóp S.ABC có áy là tam giác u cnh a. Hình chiu vuông góc ca S trên mt phng
(ABC) là im H thuc cnh AB sao cho HA = 2HB. Góc gia ng thng SC và mt phng (ABC) bng
60o. Tính th tích khi chóp S.ABC và khong cách gia hai ng thng SA và BC theo a.
Gii:

O
H
C
A
B
S
x
y
z
Gi O là trung im ca AB. Chn h trc ta  Oxyz
nh hình v.
Ta có:
,
−
,


=
  = + =

 
 = =

−
•

 
 = =
4
•
(
)

= −
;


= −
;

=
;
 
   
= − =
 
và
  
= −

.
Suy ra:
( )


  
 
 
= = =
.
B12: Cho hình chóp tam giác u S.ABC vi SA = 2a, AB = a. Gi H là hình chóp vuông góc ca A trên
cnh SC. Chng minh SC vuông góc vi mt phng (ABH). Tính th tích khi chóp S.ABH theo a.
Gii:
K
O
A
B
C
S
x
y
z
H
Gi K là hình chiu vuông góc ca S lên (ABC) thì K là tâm
ca tam giác ABC.
Gi O là trung im ca AB. Chn h trc ta  Oxyz nh
hình v.
Ta có:
−
,
,
.
 =

  = − =



= −
;
(
)

=
  
=⊥
( )
 
 
 
⊥⊥
⊥

 


= = .
Gii:
( )
  
 ==. T ây tính c
 = = .
O
A
C
D
B
x
y
z
Gi O là trung im ca CD. Chn h trc ta  Oxyz nh hình v.
Ta có:
, 
vi y > 0
T gi thit BC = BD = a ta gii ra c
= = .
V#y
.
 
= −
.
(
)


=
;
(
)

= −
.
Gi
α
là góc gia hai mt phng (ACD) và (BCD).
Ta có:
( )
  
  
 
α α
+ + −
= = = =
+ + + +
.
5
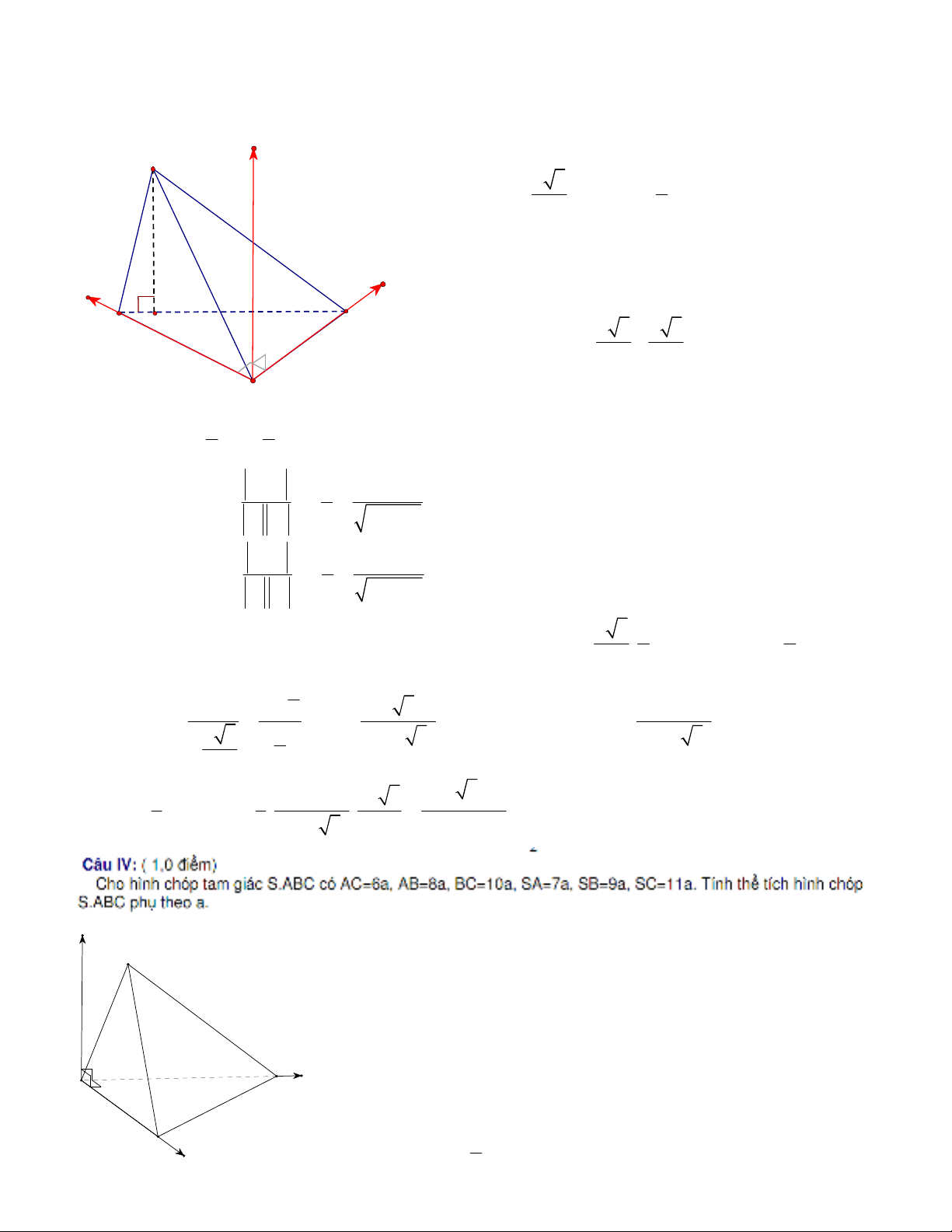
Toán hc & Tui tr: Cho hình chóp S.ABC có áy ABC là tam giác vuông ti A, BC = a và
 
=
.
Hai mt phng (SAB) và (SAC) cùng to vi áy mt góc 60o. Bit rng hình chiu vuông góc ca S trên
mt phng (ABC) thuc cnh BC. Tính th tích khi chóp S.ABC theo a.
Gii:
B
A
C
S
y
x
z
H
Chn h trc ta  Oxyz nh hình v vi gc ta  O
trùng im A.
A(0;0;0),
( )

vi

> > >
(
)
vi H là hình chiu vuông
góc ca ca S trên (ABC).
(
)
=
là vectơ pháp tuyn ca (ABC) và
 
= = −
là vectơ pháp tuyn
ca (SAB).

 
= = −
là vectơ pháp tuyn ca (SAC).
•
( )
 
 
= ⇔ = ⇔ =
+
(1)
•
( )
 
 
= ⇔ = ⇔ =
+
(2)
T (1), (2) ta có
=
. Nên
(
)
. Vì H thuc BC nên
 
= − = −
cùng
phơng, suy ra
( )
−
= ⇔ =
+
−
thay vào (1), ta c
( )
=
+
.
•
( )
(
)

 
 ∆
−
= = =
+
.
A
B
C
S
x
y
z
Chn h trc ta Oxyz nh hình v vi gc ta  O trùng
vi im A.
Ta có A(0;0;0), B(8a;0;0), C(0;6a;0), S(x;y;z) vi z>0
SA=7a

⇔ + + = (1)
SB=9a
(
)

⇔ − + + = (2)
SC=11a
(
)

⇔ + − + = (3)
Gii h (1), (2) và (3), ta c S(2a;-3a;6a).
Suy ra ng cao ca hình chóp S.ABC là
= =
.


 
= = .


=