154
•
MCA&
TðK
dây H
l
= H
max
; các nhi-t ñ8 ban ñlu t
1
= t
min
và phI t)i g
1
= g
n
; ñai vii chG ñ8 kh)o sát
t
x
= –5
0
C; g
x
= g
r
, thông sa cln tìm H
x
= H
r
.
Bưic tiGp theo – Xác ñ;nh ñ8 căng c]a dây r chG ñ8 gió c`c ñ#i. Các thông sa c]a
chG ñ8 ban ñlu không thay ñ\i. Các thông sa c]a chG ñ8 gió c`c ñ#i: t
x
= +5
0
C; q
x
= g
B
.
Thông sa tìm ñư^c H
x
= H
B
.
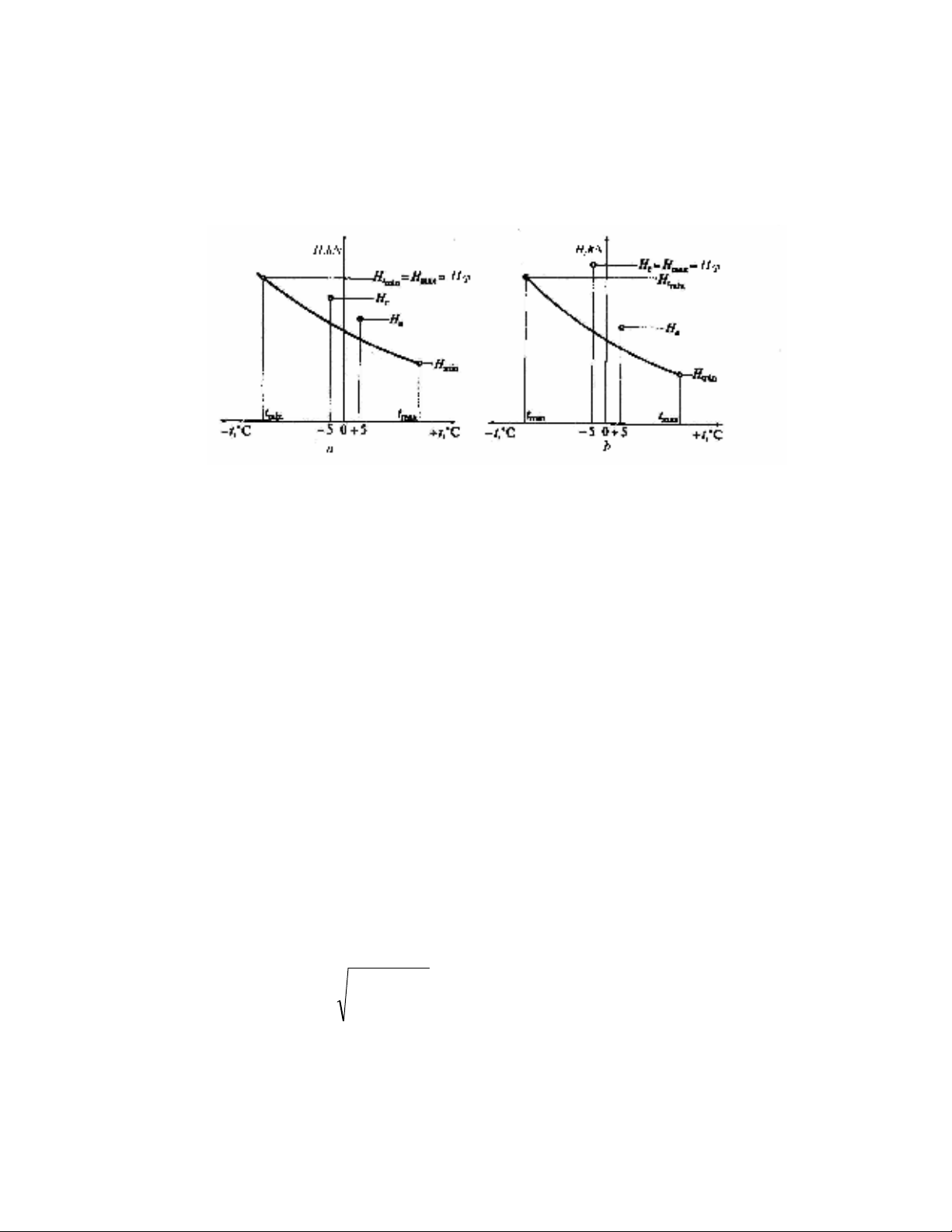
Hình 6
–
24. ðM th; ñL gi)i phương trình tr#ng thái c]a dây
a. ñ8 căng lin nhJt c]a dây r chG ñ8 nhi-t ñ8 nhO nhJt
b. ñ8 căng lin nhJt c]a dây r chG ñ8 băng tuyGt
H – ñ8 căng c]a dây
Hcp – ñ8 căng cho phép c]a dây
t – nhi-t ñ8 không khí
Trên hình 6.24b ch{ ra kGt qu) gi)i phương trình tr#ng thái c]a dây cho trưdng
h^p khi ñ8 căng lin nhJt c]a dây xuJt hi-n r chG ñ8 băng tuyGt. Trong trưdng h^p này
chG ñ8 băng tuyGt xuJt phát vii các thông sa H
t
= H
max
; t
l
= –5
0
C; q
l
= q
r
ðai vii chG ñ8 kh)o sát q
x
= g
n
. Cho các tr; sa H
x
< H
max
vii bưic nào ñó, ta nh(n
ñư^c ldi gi)i H
x
(t
x
). ðai vii ñiLm chG ñ8 gió cln ñưa vào phương trình g
x
= g
B
; t
x
=
5
0
C.
NGu dây den ñư^c k„p ch_t cHng theo giii h#n mƒi nh;p thì s` thay ñ\i ñiXu ki-n
bên ngoài den ñGn s` thay ñ\i ñ8 căng và ñ8 võng c]a dây trong mƒi nh;p theo quy lu(t
Hng vii phương trình tr#ng thái. Thông thưdng treo dây r nhkng ño#n neo th`c hi-n vii
các ñiLm di chuyLn c]a n„p (tính tii s` quay các giá chĩa, dlm chìa ho_c s` thay ñ\i
góc nghiêng chuƒi xH cách ñi-n). Trong tình huang như thG ñ8 căng c]a dây r các nh;p
chiXu dài khác nhau trong giii h#n c]a nhkng ño#n neo có thL ñư^c cân b•ng, khi mà
chiXu dài l
td
c]a m8t nh;p tương ñương nào ñó vii ñiXu ki-n nhi-t ñ8 bJt kỳ và các phI
t)i, ñ8 căng c]a dây sˆ thay ñ\i theo m8t quy lu(t như trong ño#n neo vii chiXu dài th`c
tG c]a các nh;p t#o thành, ta có:
l
td
=
a
m
i
i
ll /
1
3
∑
=
Trong ñó: l
i
– chiXu dài nh;p thH i n•m trong ño#n kh)o sát có neo.
l
a
– chiXu dài ño#n có neo
MCA&T§K
•
155
m – ca nh;p trong 1 ño#n có neo
6.4.3. TÍNH TOÁN H˜ TREO M¦T XÍCH
Nhi-m vI tính toán chính c]a h- treo xích là xác ñ;nh ñ8 căng và võng c]a
cáp mang. Cáp mang ch;u tr$ng lư^ng riêng, t)i tr$ng b\ sung t| băng tuyGt, và c) tr$ng
lư^ng c]a dây tiGp xúc vii các t)i liên quan ñGn chúng. Các phI t)i t| dây tiGp xúc
truyXn ñGn cáp mang phI thu8c vào ñ8 võng c]a dây tiGp xúc và ñ8 kéo căng c]a chúng.
Trên hình 6.25a thL hi-n sơ ñM tác dIng tương hƒ c]a dây tiGp xúc và cáp mang
khi ñ8 võng dây tiGp xúc dương. G{a thiGt sơ ñM phI t)i phân ba ñXu g
k
t| tr$ng lư^ng
c]a dây và g
kK
t| l`c căng c]a dây K, tương Hng h- treo tiGp xúc vii sa lư^ng lin các
dây treo trong m8t nh;p. T)i ñư^c truyXn t| dây tiGp xúc ñGn cáp mang g
kT
= g
k
– g
kK
.
T)i g
kK
ñư^c xác ñ;nh:
g
kK
= 8fk/l
2
(6.8)
Trong ñó: f – ñ8 võng c]a dây tiGp xúc, m
k – ñ8 căng c]a dây tiGp xúc, kN
l – chiXu dài nh;p, m
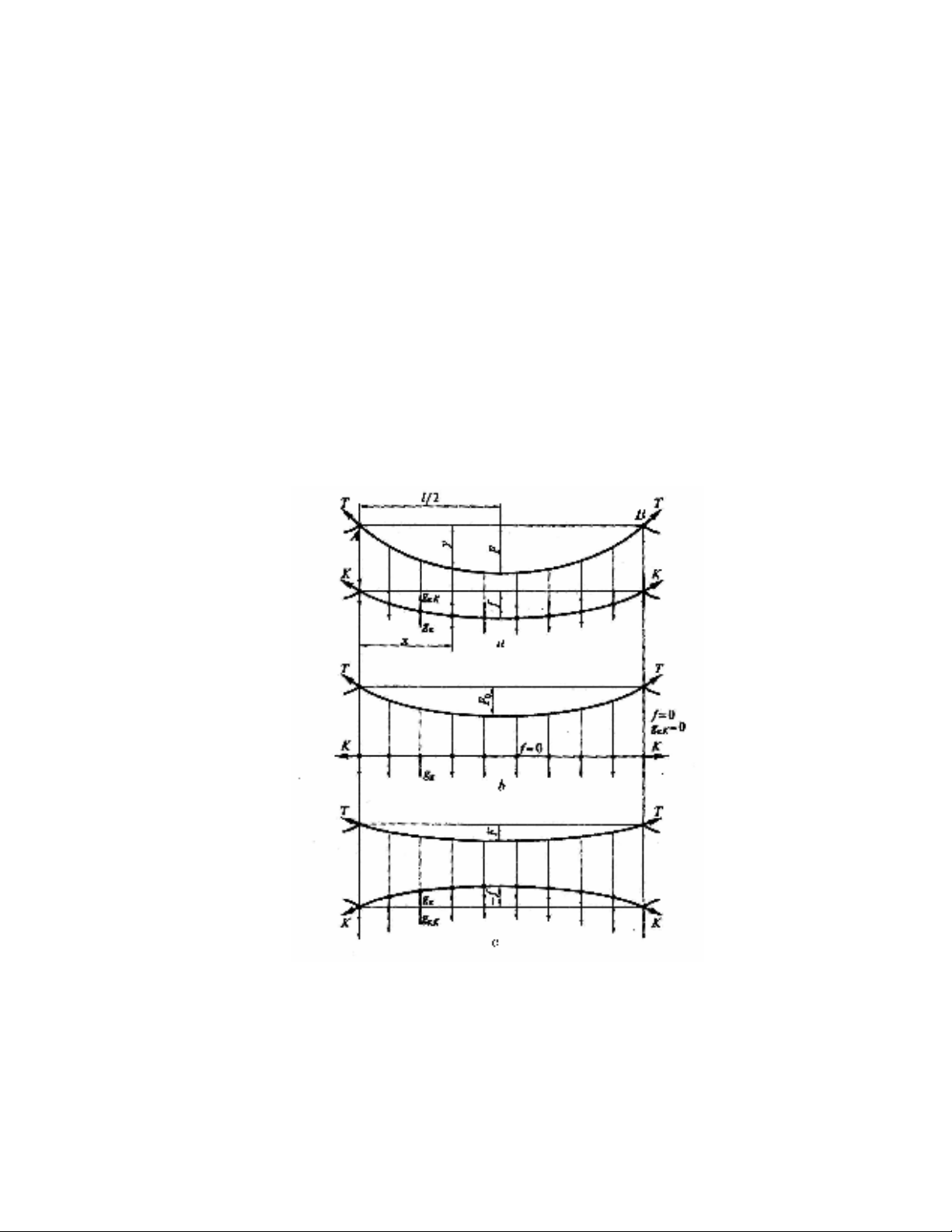
Hình 6
–
25. Các sơ ñM tác dIng qua l#i c]a dây tiGp xúc
và cáp treo c]a h- treo ñơn gi)n trong các chG ñ8 khác nhau
a. ñ8 võng dương c]a dây tiGp xúc;
b. chG ñ8 không võng;
c. ñ8 võng âm c]a dây tiGp xúc;
156
•
MCA&
TðK
A,B– các ñiLm k„p dây mang c]a h- treo tiGp xúc;
l– chiXu dài nh;p;
T– ñ8 căng c]a cáp;
K– ñ8 căng c]a dây tiGp xúc;
F– ñ8 võng c]a cáp treo;
F
0
– ñ8 võng c]a cáp mang r chG ñ8 không võng;
f– ñ8 võng c]a dây tiGp xúc;
g
k
– phI t)i t| tr$ng lư^ng c]a dây tiGp xúc;
g
kK
– l`c tác dIng tương hƒ gika cáp mang và dây tiGp xúc;
y– tung ñ8 ñ8 võng c]a cáp mang trong m_t cWt ngang vii hoành ñ8 x.
Trên hình 6.25b chG ñ8 không võng c]a h- treo mWt xích, sơ ñM có s` tác dIng
tương hƒ c]a dây tiGp xúc và cáp mang khi nhi-t ñ8 môi trưdng gi)m làm gi)m chiXu
dài c]a cáp mang và gi)m ñ8 võng c]a nó ñGn giá tr; F
0
. Trong chG ñ8 này tr$ng lư^ng
dây tiGp xúc ñư^c truyXn hoàn toàn cho cáp mang. Khi nhi-t ñ8 tiGp tIc gi)m và gi)m
chiXu d)i c]a cáp mang,sˆ xuJt hi-n ñ8 võng âm c]a dây tiGp xúc (Hình6.25c). L`c kéo
căng dây tiGp xúc t#o thành l`c phân ba ñXu và hưing xuang dưii. T)i phân ba ñXu g
kK
ñMng thdi hưing xuang dưii, còn cáp mang ngoài tr$ng lư^ng dây tiGp xúc và các dây
tăng cưdng còn ch;u t)i g
kK
t| ñ8 căng c]a dây tiGp xúc.
g
kT
= g
k
+ g
kK
Tr#ng thái c]a cáp mang ñư^c biLu hi-n bri phương trình ñưdng võng. Các
phương án có thL c]a phương trình dlm võng phI thu8c vào tính chJt c]a mô hình h-
treo (mWt) xích lJy làm cơ sr tính toán. Kh)o sát mô hình vii sa lư^ng lin các dây treo
tiGp xúc chiGu toàn b8 nh;p t| ñiLm k„p dây treo này ñGn dây treo khác (Hình 6.25.a).
Thành phln thŠng ñHng c]a l`c căng V, kN, c]a cáp r các ñiLm k„p A và B ñư^c
xác ñ;nh:
V
A
= V
B
= g
TX
l/2
Trong ñó: g
TX
– thành phln thŠng ñHng c]a phI t)i h^p thành c]a cáp mang r
chG ñ8 tính toán, kN/m
Mô men uan, kNm, trong m_t phŠng thŠng ñHng trong m_t cWt c]a cáp mang tính
ñGn kho)ng cách x t| ñiLm A.
Mx = VAx – gTXx2/2 = gTXlx/2 – gTXx2/2 = gTXx(l–x)/2
Tung ñ8 y ñ8 võng c]a cáp trong m_t cWt vii hoành ñ8 x liên quan vii ñ8 căng
c]a cáp T như sau: y = Mx/T. Sau khi ñ_t Mx nh(n ñư^c y = gTXx(l–x)/(2T), ho_c sau
khi thay gTX = gx – gkK
y = (gx–gkK)x(l–x)/(2T)
Trong ñó: gx– t)i thŠng ñHng ñGn cáp treo t| tJt c) các dây c]a h- treo mWt xích.
Tính tii công thHc 6–8 nh(n ñư^c
y = (gx–8fK/l2)x(l–x)/(2T)
T#i ñiLm gika c]a nh;p,ñ8 trùng c]a cáp y b•ng ñ8 võng c]a nó F
MCA&T§K
•
157
F = gxl2/(8T) – fK/T (6.9)
T| ñó ta nh(n ñư^c công thHc tính ñ8 căng c]a cáp
T = gxl2/(8F) – fK/F (6.10)
Khi ñ8 võng c]a dây tiGp xúc f = 0, ñ8 căng c]a cáp ñư^c xác ñ;nh
T0 = g0l2/(8F0) (6.11)
Trong ñó: g0– tr$ng lư^ng c]a dây den, dây căng và cáp c]a h- treo xích
F0– ñ8 võng c]a cáp mang khi không ch;u l`c treo dây tiGp xúc
T| nhkng biLu thHc nh(n ñư^c r trên thly r•ng tính toán cáp mang c]a h- treo
xích giang như tính dây treo t` do nhưng vii t)i biGn ñ\i, tr; sa c]a nó phI thu8c s`
thay ñ\i nhi-t ñ8 và ñư^c qui ưic bri tác dIng c]a ñ8 căng dây tiGp xúc truyXn qua các
dây căng ñGn cáp mang
Kh)o sát chG ñ8 tính toán nào ñó trong ñó các thông sa ñư^c ký hi-u x.
ð8 võng c]a dây tiGp xúc fx liên quan ñGn ñ8 võng c
]a cáp mang Fx bri
biLu thHc:
fx = Fx – F0 (6.12)
S= dIng công thHc 6–9, 6–11 và 6–12,ta nh(n ñư^c:
Fx = l2(gx+g0K/T0)/[8(Tx+K)],
Có thL ñ_t dưii d#ng:
Fx = l2gtdx/(8Zx)
Trong ñó: gtdx– phI t)i tương ñương, kN/m;
Zx– ñ8 căng tính ñ\i, kN
6.4.4.TÍNH TOÁN ðÀN H’I CA LƯÏI TIÓP XÚC
Khi ép cln tiGp ñi-n lên dây tiGp xúc sˆ chuyLn d;ch dây theo chiXu thŠng ñHng,
Quan h- s` chuyLn d;ch c]a dây vii l`c gây nên s` chuyLn d;ch g$i là ñ8 ñàn hMi λ c]a
m#ng tiGp xúc. ThHc nguyên c]a ñ8 ñàn hMi λ là mm/N, hay m/kN. ðL b)o ñ)m lJy ñi-n
tin c(y,cln chWc chWn không ch{ chiXu cao giang nhau c]a dây tiGp xúc so vii m_t
ñưdng trong ph#m vi chiXu d)i c]a nh;p, mà còn ca ñ;nh ñ8 ñàn hMi
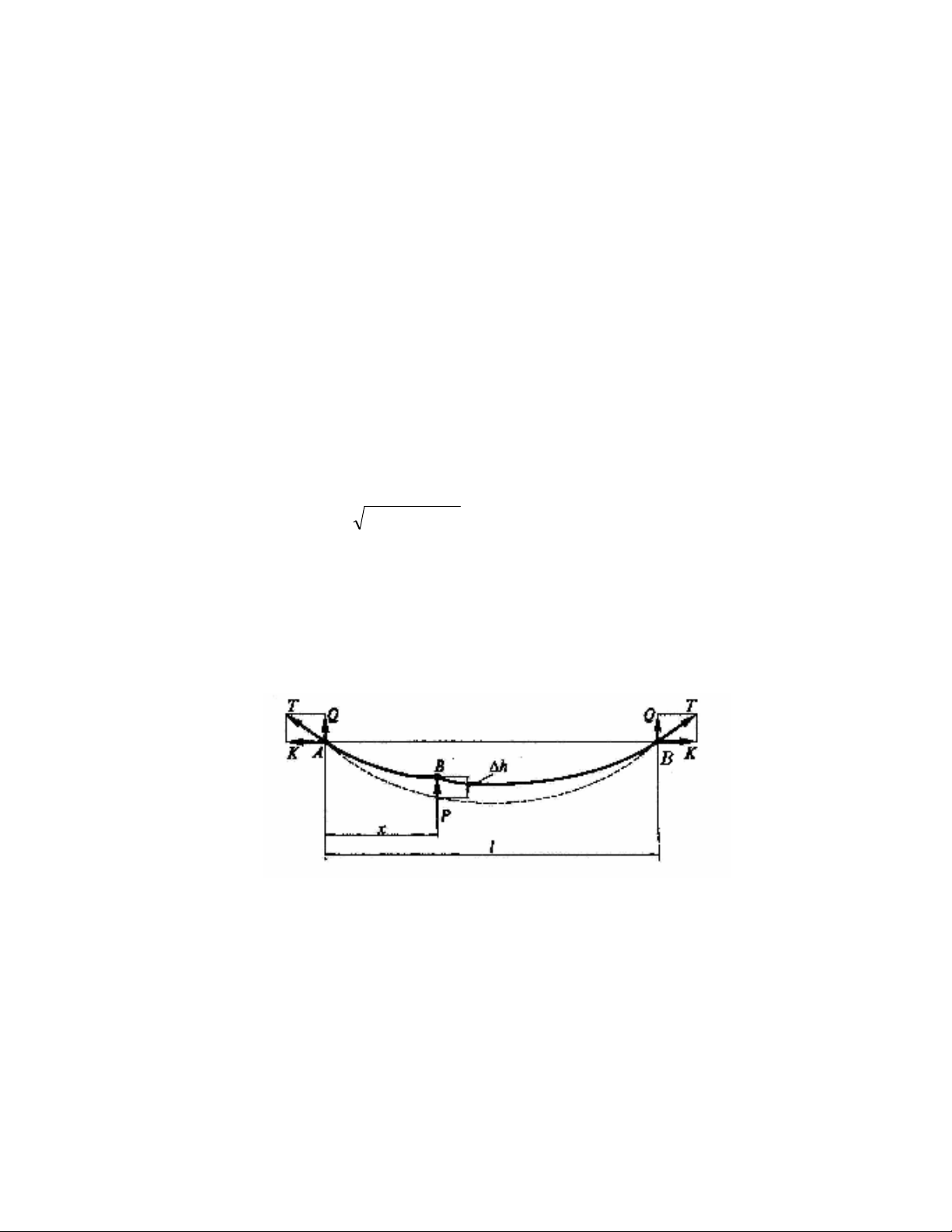
Trên hình 6.26 là sơ ñM biGn ñ\i v; trí c]a dây h- treo ñơn gi)n khi k„p ch_t các
ñlu dây A và B trên các trI ñg và ép cln tiGp ñi-n lên dây vii l`c P r ñiLm vii to# ñ8 x.
Dưii tác dIng c]a l`c ép, thành phln thŠng ñHng c]a ph)n l`c r ñiLm k„p dây gi)m
xuang. Chúng ta xét ño#n dây AB: Sau khi chuyLn d;ch ñiLm B ñGn chiXu cao h và
gi)m thành phln thŠng ñHng c]a phln l`c trI r ñiLm A ñGn Q = P(l–x)/l dây gik
nguyên tr#ng thái cân b•ng. Như v(y, t\ng s` thay ñ\i mômen l`c tương Hng ñiLm tác
dIng c]a l`c ép cln tiGp ñi-n b•ng 0 và Q
x
= Kh. Dư
ii d#ng khai triLn ta có
P(l–x)x/l = Kh, t| ñó ta nh(n ñư^c biLu thHc cho ñ8 ñàn hMi:
λ = (l–x)x/(lK) (6.14)
T| biLu thHc 6.14 thJy r•ng tính ñàn hMi λ c]a h- treo ñơn gi)n t#i các ñiLm k„p
dây tiGp xúc b•ng không và thay ñ\i trong kho)ng dài c]a nh;p và là ñiLm không chJp
nh(n cho vi-c tiGp nh(n ñi-n năng.
158
•
MCA&
TðK
Các ch{ tiêu ñàn hMi tat là h- treo mWt xích. Tính toán ñ8 ñàn hMi ñư^c tiGn hành
tính tii tác dIng tương hƒ c]a cáp mang và dây tiGp xúc. Tính chJt tác dIng qua l#i thay
ñ\i theo chiXu dài c]a nh;p và vì thG vi-c tính toán tiGn hành theo các công thHc khác
nhau ñai vii 3 vùng trong m8t nh;p. Như ñai vii h- treo lò xo ñơn ngưdi ta chia vùng I
t#i nút lò xo, vùng II t| vùng cuai vùng I ñGn ñiLm cuan vùng III (Hình6.27).
Có thL áp dIng các công thHc sau ñây cho h- treo xích:
ðai vii vùng III ñ8 ñàn hMi, m/kN:
λ
III
= x(l–x)/(l(T+K)) + x
0
T(c–x
0
)/(cK(T+K))
Trong ñó: x– kho)ng cách t| ñiLm k„p A ñGn ñiGp ñi-n,m
x
0
– kho)ng cách t| dây căng gln nhJt ñGn cln tiGp ñi-n,m
T,K– Các l`c căng tương Hng c]a cáp và dây tiGp xúc, kN
c– Kho)ng cách gika các dây căng, m
– Trong vùng I dưii cáp lò xo tính ñàn hMi ñư^c xác ñ;nh:
λ
I
= [2(T–H
P
)γ/d + 2(K+H
P
)/l]
–1
Trong ñó: H
P
– ñ8 căng c]a cáp lò xo, kN
γ– H- sa ñư^c xác ñ;nh theo biLu thHc
γ = 0,6
)/)(/( TKed
,
Trong ñó: d– kho)ng cách t| c8t ñGn ñiLm k„p cáp lò xo,m
e– kho)ng cách t| c8t ñGn dây căng ñơn gi)n gln nhJt, m (xem hình
6.27)
– ð8 ñàn hMi trong vùng II
λ
II
= [e(L–e)]/{l[T+K–(K+H
P
)β]}
Trong ñó: β = (d/e)(1–0,05d) khi là h- dây căng ñơn gi)n β=0
Hình 6
–
26. Sơ ñM ñL tính ñ8 ñàn hMi c]a lưii tiGp xúc
A,B– Các ñiLm k„p c]a h- tiGp xúc;
l– chiXu dài c]a nh;p;
h– s` thay ñ\i chiXu cao c]a dây khi ép cln tiGp ñi-n lên dây tiGp
xúc vii l`c P;
K,Q– thành phln n•m ngang và thŠng ñHng c]a l`c ép T;
x– hoành ñ8 c]a ñiLm B ép cln tiGp ñi-n.