
Tạp chí KHOA HỌC – Trường Đại học Quốc tế Hồng Bàng Số 10.2019:67–78 67
Journal Of Science – Hong Bang International University ISSN: 2615 – 9686
1. GIỚI THIỆU
Ngày nay, chuỗi cung ứng càng khẳng định
rõ hơn vai trò của mình trong quá trình vận
hành của các tổ chức kinh doanh. Trong thời
kỳ công nghiệp hóa, hiện đại hóa, và quá trình
cạnh tranh gay gắt như hiện nay, chuỗi cung
ứng trong ngành công nghiệp thực phẩm nói
chung và ngành chế biến dầu thực vật nói
riêng phải không ngừng cải ến, nâng cao
năng lực vận hành, phát huy các chiến lược
sắc bén nhằm giúp tăng cường cạnh tranh sức
mạnh của doanh nghiệp trên thương trường
trong nước và xuất khẩu. Cũng giống như
trong các ngành công nghiệp khác, ngành chế
biến dầu thực vật đòi hỏi có nguồn đầu vào
rất phong phú và đa dạng, nhưng để m được
nguồn nguyên liệu phù hợp với ngành và đặc
biệt là không gây tác động êu cực đến môi
trường thì đó là vấn đề nan giải của các tổ
chức, công ty/doanh nghiệp.
Theo đánh giá của Bộ Công thương, ngành
dầu thực vật Việt Nam thời gian qua đã không
ngừng lớn mạnh và ngày càng có những đóng
góp ch cực vào nền kinh tế quốc dân. Tuy
nhiên, điểm yếu nhất của ngành dầu thực vật
là trên 90% nguyên liệu phải nhập khẩu [15].
Vì vậy việc m nguồn cung cấp tối ưu là một
quyết định vô cùng quan trọng. Do đó, những
người ra quyết định phải đánh giá rất nhiều
yếu tố, bao gồm cả định nh và định lượng
khi quyết định lựa chọn nguồn nguyên liệu
vừa để đảm bảo các mục êu về kinh tế, vừa
đảm bảo về yếu tố tác động môi trường [21].
NGHIÊN CỨU MÔ HÌNH RA QUYẾT ĐỊNH ĐA TIÊU CHÍ ĐỂ ĐÁNHGIÁ VÀ LỰA CHỌN NHÀ CUNG CẤP NGUYÊN LIỆU CHO NGÀNH CHẾ BIẾN DẦU THỰC VẬTNguyễn Văn Thành*, Nguyễn Viết Tịnh, Nhiêu Nhật LươngTrường Đại học Quốc tế Hồng Bàng
TÓM TẮTThị trường kinh doanh toàn cầu ngày càng khốc liệt. Để tồn tại và phát triển, mỗi đơn vị kinh
doanh không ngừng nâng cao năng lực sản xuất, đáp ứng nhu cầu ngày càng cao của khách
hàng. Trong bất kỳ một chuỗi cung ứng nào, lựa chọn nhà cung cấp tối ưu và hiệu quả là một
quyết định cực kỳ quan trọng, tác động và ảnh hưởng trực ếp đến hiệu quả vận hành của
toàn chuỗi. Do đó, nhóm tác giả đã đề xuất mô hình ra quyết định đa êu chí (Mul criteria
Decision Making Model - MCDM) bao gồm mô hình phân ch thứ bậc mờ (Fuzzy Analy c
Hierarchy Process - FAHP) và mô hình bao dữ liệu (Data Envelopment Analysis) để đánh giá
và lựa chọn nhà cung cấp bền vững, được áp dụng tại doanh nghiệp sản xuất dầu thực vật.
Đóng góp của nghiên cứu này là trình bày một mô hình MCDM mới và mở rộng có thể áp
dụng trong ngành công nghiệp thực phẩm, ngoài ra cũng có thể áp dụng rộng rãi trong những
ngành công nghiệp khác.
Từ khóa: MCDM, FAHP, DEA, dầu thực vật.
* TS. Nguyễn Văn Thành – Trường Đại học Quốc tế Hồng Bàng
Tạp chí KHOA HỌC – Trường Đại học Quốc tế Hồng Bàng Số 10.2019:67–78
68
Journal Of Science – Hong Bang International University
ISSN: 2615 – 9686
Để giải quyết được vấn đề này, lý thuyết tập
mờ của Zadeh là một công cụ hiệu quả để
lượng hóa các thông n mang nh mơ hồ và
không đầy đủ trong quá trình ra quyết định
[20]. Chính vì lý do trên, bài “Nghiên cứu mô
hình ra quyết định đa êu chí để đánh giá và
lựa chọn nhà cung cấp nguyên liệu cho ngành
chế biến dầu thực vật” được thực hiện nhằm
khắc phục vấn đề trên. Đầu ên, mô hình
FAHP được áp dụng để xác định trọng số
của tất cả các nhà cung ứng ềm năng dựa
trên ý kiến từ các chuyên gia của công ty.
Sau đó, mô hình DEA được áp dụng để xếp
hạng tất cả các nhà cung cấp ềm năng.
Mục êu chính của nghiên cứu này là trình
bày một cách ếp cận mới, ch hợp FAHP
và DEA để lựa chọn nhà cung cấp trong
môi trường ra quyết định không chắc chắn.
2. LƯỢC KHẢO TÀI LIỆU
2.1. Khái niệm sản xuất bền vững
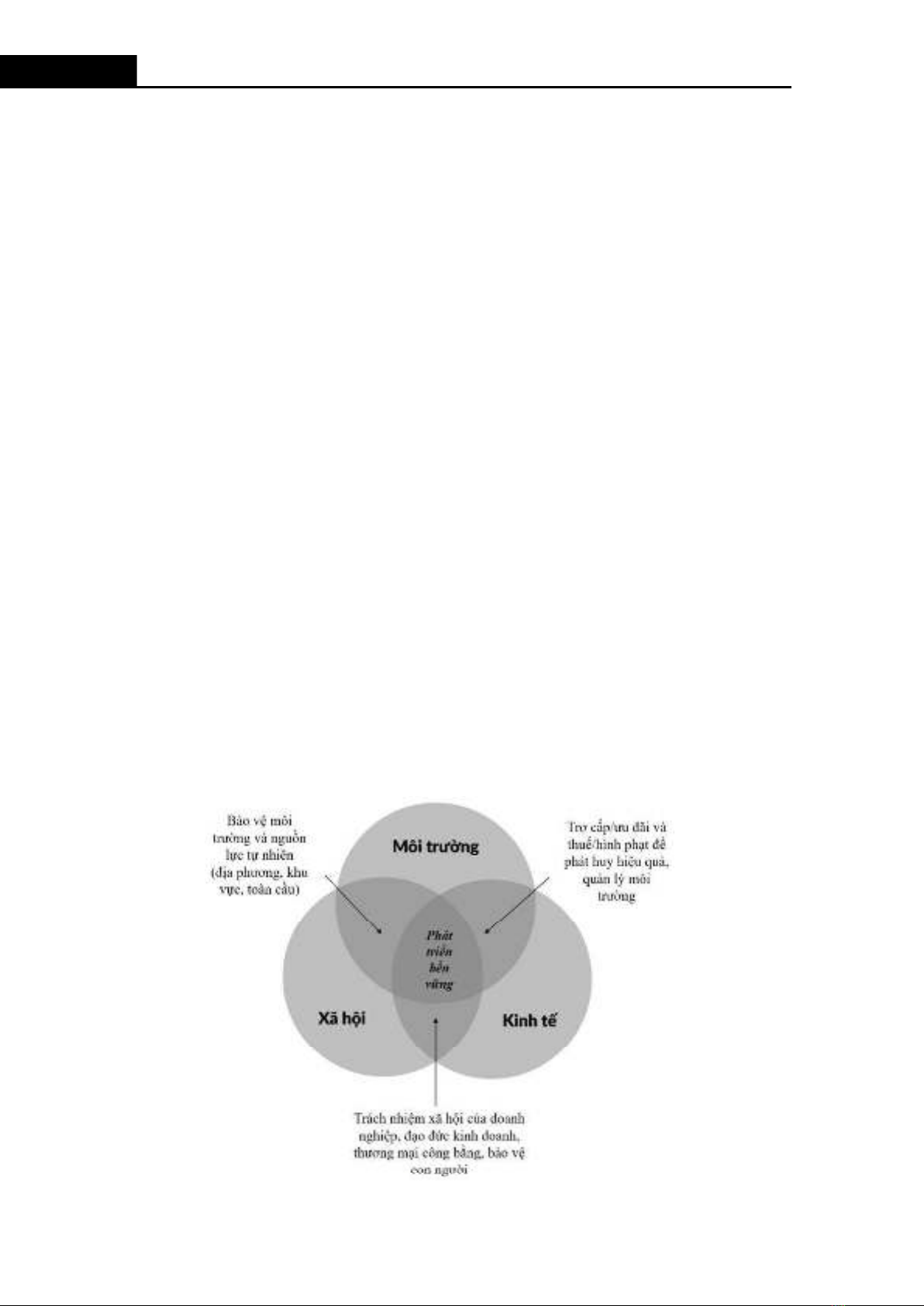
Qua Hình 1 cho ta thấy sự tương tác lẫn nhau
giữa ba yếu tố môi trường, xã hội và kinh tế.
Môi trường và xã hội tác động qua lại tạo
khả năng phát triển bền vững cho việc bảo
vệ môi trường và nguồn lực tự nhiên (địa
phương, khu vực, toàn cầu). Môi trường
tương tác đến kinh tế tạo ra sự bền vững
cho việc trợ cấp/ưu đãi và thuế/hình phạt để
phát huy nh hiệu quả, quản lý môi trường.
Xã hội và kinh tế tương tác tạo sự bền vững
trong trách nhiệm của doanh nghiệp, đạo
đức kinh doanh, thương mại công bằng và
để bảo vệ con người.
Theo Edward (2019) [9], sản xuất bền vững
được định nghĩa “Sản xuất bền vững là tạo ra
sản phẩm và dịch vụ sử dụng các quá trình và
hệ thống”, mà:
− Không ô nhiễm;
− Bảo tồn năng lượng và tài nguyên thiên
nhiên;
− Hiệu quả kinh tế;
− An toàn và lành mạnh cho công nhân, cộng
đồng và người êu dùng;
− Mang lại khích lệ mang nh xã hội và nh
sáng tạo cho tất cả lao động.
Để đạt được sự bền vững trong hoạt động
sản xuất, nh bền vững cần được kết hợp
Hình 1. Khái niệm sản xuất bền vững [13]
Tạp chí KHOA HỌC – Trường Đại học Quốc tế Hồng Bàng Số 10.2019:67–78 69
Journal Of Science – Hong Bang International University ISSN: 2615 – 9686
trong tất cả các giai đoạn của tổ chức chuỗi
cung ứng. Lựa chọn nhà cung cấp đóng vai
trò quan trọng, đóng góp vào các hoạt động
kinh doanh. Lựa chọn nhà cung cấp và quản
lý phù hợp giúp các tổ chức giảm chi phí đầu
vào, cải thiện chất lượng hàng hóa và dịch
vụ cung cấp cho khách hàng và cải thiện khả
năng cạnh tranh thị trường.
2.2. Lý thuyết tập mờ
Lý thuyết tập mờ được giới thiệu bởi tác
giả Zadeh với nội dung là nhằm giải quyết
những vấn đề có tính chất không chắc
chắn do sự thiếu chính xác hoặc thiếu rõ
ràng. Lý thuyết tập mờ có thể được ứng
dụng ở nhiều lĩnh vực khác nhau như trí
tuệ nhân tạo, khoa học máy tính, y học, lý
thuyết ra quyết định,... [23].
Xét x là tập hợp gồm các phần tử. Tập mờ
là một tập hợp được biểu diễn dưới dạng
một hàm thành viên μM() thể hiện khả
năng để thuộc vào tập M. Giá trị biểu diễn
mức độ thành viên của một phần tử nằm
trong khoảng từ 0 tới 1. Nếu μM() = 0 có
nghĩa phần tử hoàn toàn không thuộc tập
M và ngược lại nếu μM() = 1 có nghĩa phần
tử hoàn toàn thuộc tập M [14].
Khái niệm số mờ (fuzzy number) được Zadeh
đề xuất [23] để diễn tả một đại lượng mà giá
trị của nó không thể đo lường chính xác. Có
rất nhiều dạng số mờ, nhưng dạng số mờ
tam giác (triangle fuzzy number) thường được
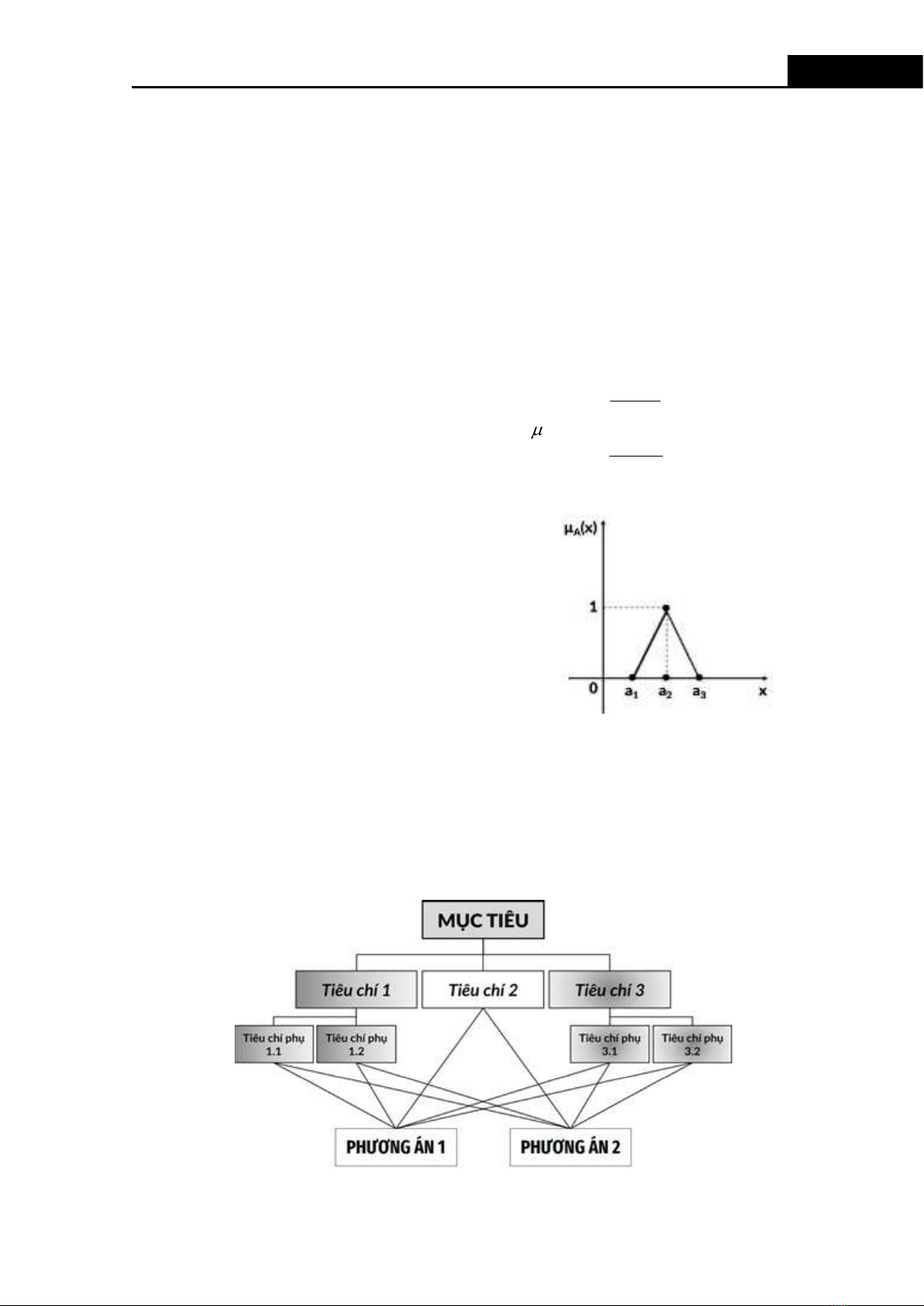
dùng phổ biến nhất. Số mờ dạng tam giác
được biểu diễn bằng một bộ 3 số thực (a1 ,
a2 , a3) và biểu diễn thông qua hàm thành
viên như Hình 2 sau [7]:
Hình 2. Số mờ dạng tam giác(Diouf & Choonjong, 2018)2.3. Cơ sở toán học trong
phương
pháp AHP
2.3.1. Tiếp cận
phương
pháp AHP
Phân ch thứ bậc - Analy c Hierarchy Pro-
Hình 3. Phương pháp AHP [11]
1
1
1 2
2 1
3
2 3
3 2
3
0,
,
( )
,
0,
M
x a
x a a x a
a a
a x a x a
a a
x a
x 1

Tạp chí KHOA HỌC – Trường Đại học Quốc tế Hồng Bàng Số 10.2019:67–78
70
Journal Of Science – Hong Bang International University
ISSN: 2615 – 9686
cess (AHP) - là một phương pháp so sánh
định lượng được sử dụng để chọn một giải
pháp ưa thích bằng cách sử dụng cặp so sánh
của các giải pháp dựa trên hiệu quả tương đối
của chúng đối với êu chí.
AHP là một phương pháp ra quyết định đa
mục êu được đề xuất bởi Saaty (1980) [17].
Dựa trên so sánh cặp, AHP có thể được mô
tả với 3 nguyên tắc chính: phân ch, đánh giá
và tổng hợp. Trước ên, AHP phân ch một
vấn đề phức tạp, đa êu chí theo cấu trúc thứ
bậc như Hình 3.
Sơ đồ cấu trúc thứ bậc bắt đầu với mục
êu, được phân ch qua các êu chí lớn và
các êu chí thành phần, cấp bậc cuối cùng
thường bao gồm các phương án có thể lựa
chọn. Quá trình đánh giá sử dụng ma trận so
sánh cặp với thang điểm 9, xác định trọng số
dựa trên vector riêng ứng với giá trị riêng lớn
nhất, sau đó kiểm tra hệ số nhất quán. Cuối
cùng, tất cả các trọng số được tổng hợp lại để
đưa ra quyết định tốt nhất.
Phương pháp này bắt đầu từ việc xây dựng sơ
đồ cây thứ bậc, bao gồm một số bước so sánh
từng cặp êu chí, từng cặp phương án theo
êu chí. Kết quả so sánh chính là trọng số.
Đặc điểm của phương pháp AHP là việc nh
toán tỉ số tương quan. Trong thực tế, không
phải lúc nào cũng có thể thiết lập được quan
hệ bắc cầu trong khi so sánh từng cặp (ví dụ
phương án A có thể tốt hơn phương án B,
phương án B có thể tốt hơn phương án C).
AHP có thể giúp xác định và đánh giá lượng
hóa các êu chí, phân ch các dữ liệu thu
thập được theo các êu chí đó, và thúc đẩy
việc ra quyết định nhanh hơn, chính xác hơn.
Nó giúp cân nhắc và đo lường các yếu tố cả
về chủ quan và khách quan, tạo nên một cơ
chế hữu dụng để đảm bảo nh nhất quán
trong việc đánh giá, đo lường các giải pháp và
các đề xuất được đưa ra trong nhóm làm việc.
Một trong những kỹ thuật phân ch phổ biến
nhất cho vấn đề ra quyết định phức tạp là quá
trình phân ch phân cấp (AHP), đây là một
cách ếp cận để ra quyết định đa chỉ êu, liên
quan đến cấu trúc các êu chí nhiều lựa chọn
đầu vào một hệ thống phân cấp, đánh giá tầm
quan trọng tương đối các êu chí, so sánh
lựa chọn thay thế cho từng êu chí và
xác định một bảng xếp hạng chung của các
lựa chọn thay thế. Kết quả của AHP được xếp
hạng ưu ên sự ưa thích tổng thể cho mỗi
giải pháp quyết định cuối cùng giúp người ra
quyết định có lựa chọn tốt nhất
2.3.2. Phương pháp AHP mờ
Phương pháp phân ch thứ bậc mờ - Fuzzy
Analy c Hierarchy Process (FAHP) - là một
phương pháp phân ch nâng cao được phát
triển từ AHP. Mặc dù AHP khá phổ biến
nhưng phương pháp này thường không đạt
hiệu quả cao vì không có khả năng xử lý đầy
đủ sự không chắc chắn vốn có và sự không
chính xác liên quan đến việc lập bảng trọng
số các êu chí của người ra quyết định tới
các con số chính xác. Trong phương pháp
FAHP, tỷ lệ so sánh mờ được sử dụng để
có thể chỉ ra được sự không rõ ràng. Người
ra quyết định muốn sử dụng sự không chắc
chắn trong khi thực hiện các so sánh của các
lựa chọn thay thế. Để lấy sự không chắc chắn
về số lượng phức tạp đã được sử dụng thay
vì các con số sắc nét, phương pháp này được
đề xuất bởi Cheng và Hwang [6].

Tạp chí KHOA HỌC – Trường Đại học Quốc tế Hồng Bàng Số 10.2019:67–78 71
Journal Of Science – Hong Bang International University ISSN: 2615 – 9686
Quy trình thực hiện phương pháp FAHP
như sau:
− Bước 1: Xác định các êu chí và êu chí phụ.
− Bước 2: So sánh, đánh giá theo cặp (Pair-
wise comparison).
− Bước 3: Xây dựng các ma trận FAHP.
− Bước 4: Tính toán trọng số mờ theo phương
pháp Giá trị trung bình hình học (Geometric
mean) [4].
− Bước 5: Xếp hạng các phương án bằng
phương pháp TNF (Center of Area).
2.4. Mô hình phân ch đường bao dữ
liệu (Data Envelopment Analysis - DEA)
Phương pháp phân ch đường bao dữ liệu
(Data Envelopment Analysis - DEA) được
phát triển bởi Charnes, Cooper và Rhodes
(1978) [5]. Phương pháp này đã được ứng
dụng và mở rộng ra để đánh giá hiệu quả
tương đối của nhiều yếu tố đầu vào, nhiều
yếu tố đầu ra của các đơn vị ra quyết định
(Decision Making Units - DMUs).
Hiện nay, DEA được nhiên cứu rộng rãi và
đang được áp dụng trong nhiều lĩnh vực khác
nhau trên thế giới như ngành nông nghiệp
[19], ngành ngân hàng [2], ngành giáo dục
[16], ngành hàng không [22], các tổ chức y tế
[3], chuỗi cung ứng, dịch vụ [1],…
Một cách đơn giản, hiệu quả (mang nh kỹ
thuật) của việc sử dụng yếu tố đầu vào x
để thu được yếu tố đầu ra y có thể được
đo lường theo công thức:
Công thức (2) chỉ có thể được áp dụng trong
trường hợp chỉ có 1 biến đầu vào (input) và
1 biến đầu ra (output). Ví dụ như hiệu quả sử
dụng vốn (doanh thu/vốn) hay hiệu quả sử
dụng lao động (thu nhập/lao động). Khi áp
dụng cho một doanh nghiệp (hay gọi chung là
một đơn vị ra quyết định - DMU) có k yếu tố
đầu vào và sản xuất ra m kết quả đầu ra, thì
cần phải dựa trên giá cả pi và wj của các yếu
tố đầu vào/đầu ra đó để nh toán [10]:
Tuy nhiên, việc xác định giá cả của từng yếu
tố đầu vào/đầu ra thường rất phức tạp, nhất
là trong những lĩnh vực như tài chính ngân
hàng, giáo dục đào tạo,… Trong trường hợp
này, có thể giả thiết là mỗi DMU sẽ sử dụng
những trọng số nhất định um và vk sao cho
điểm hiệu quả TE của nó là cao nhất, nói cách
khác, um và vk là những trọng số giúp cho
DMU đó ến gần đến đường giới hạn khả
năng sản xuất PPF nhất. Vì vậy, chúng còn
được gọi là “giá ẩn” (shadow prices) vì mặc dù
chúng không phải là giá cả thực (true prices)
nhưng lại đóng vai trò như giá cả trong việc
nh toán hiệu quả kỹ thuật TE [8].
Một cách tổng quát, với bài toán có n DMU,
mỗi DMU sử dụng k yếu tố đầu vào xk để tạo
ra m yếu tố đầu ra ym, việc xác định hiệu quả
TE0 của một DMU0 bất kỳ sẽ được nh toán
như sau:
,( )
u v 0
max TE 4
Với điều kiện:
0 0
0
0 0
TE m m
k k
u y
v x
Dau ra y
= ( )
Dau vao x
TE 2
Tong Dau ra
( )
Tong Dau vao
1 1 m m
1 1 k k
p y p y
TE 3
w x w x






















![Câu hỏi ôn tập Xuất nhập khẩu: Tổng hợp [mới nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251230/phuongnguyen2005/135x160/40711768806382.jpg)



