Present to trang ----------------------------
havemind
2 NHỮNG CÔNG THỨC TÍNH NHANH DAO ĐỘNG ĐIỀU
HOÀ
I.Đại cương về dao động điều hoà
1.Đồ thị.
Đồ thị của li độ x theo t có dạng là đường hình sin
Đồ thị của vận tốc v theo thời gian t có dạng là đường hình sin
Đồ thị của vận tốc v theo li độ x có dạng là đường Elip (E)
Đồ thị của gia tốc a theo thời gian có dạng là đường hình sin
Đồ thị của gia tốc a theo li độ x là đoạn thẳng
Đồ thị của gia tốc a theo vận tốc v có dạng là đường Elip (E)
2.Độ lệch pha
- li độ chậm pha hơn vận tốc một góc 90* hay vuông pha với vận tốc
- li độ chậm pha hơn gia tốc một góc 180* hay ngược pha vơi gia tốc
- vận tốc nhanh pha hơn li độ một góc 90* và chậm pha hơn gia tốc một góc 90*
- gia tốc nhanh pha hơn li độ một góc 90* và cũng nhanh pha hơn vận tốc một góc 180*
3.Chú ý
-Khi vật chuyển động từ VT biên về VTCB là chuyển động nhanh dần nhưng không đều : a.v > 0
-Khi vật chuyển động từ VTCB ra VT biên là chuyển động chậm dần nhưng không đều : a.v < 0
-Khi vật đi qua VTCB thì hơp lực tác dụng vào vật đổi chiều
-Vật đổi chiều chuyển động khi hợp lực tác dụng vào vật có độ lớn cực đại và vật đang ở VT biên
II.Chu kỳ dao động và sự thay đổi chu kì
A.CON LẮC L Ò XO
Gọi T1 là chu kỳ của con lắc lo xo có khối lượng m1,k1
T2 m2,k2
T m,k
m = m1 + m2 ----> T² = (T1)² + (T2)²
m = m1 - m2 ----> T² = (T1)² - (T2)²
*2 lò xo nối tiếp 1/k = 1/k1 + 1/k2 ------> T² = (T1)² + (T2)²
*2 lò xo song song k = k1 + k2 ------> 1/T² = 1/(T1)² + 1/(T2)² (thuộc mấy ct này nha em)(:-*)
Havemind
1
Present to trang ----------------------------
havemind
Bài tập ví dụ:
1.Hai lò xo có cùng chiều dài tự nhiên. Khi treo vật có khối lượng m bằng lò xo có k1 thì nó dao động
với chu kỳ T1 = 3s. Thay bằng lò xo có độ cứng k2 thì chu kỳ là T2 = 4s. Nối 2 lò xo lại thành 1 rồi
gắn vật m vào thì chu kỳ dao động mới là T = ?
Giải: Vì 2 lò xo mắc nối tiếp nên: T² = (T1)² + (T2)² ----> T1 = 5s
-----------------------------------------------------------
B.CON LẮC ĐƠN
I.Sự phụ thuộc của chu kỳ vào chiều dài l:
- Gọi T1 là chu kỳ của con lắc đơn ứng với chiều dài l1
T2 ------ l2
T ---- l= l1+l2
- Ta có: T² = T1² + T2² (thuộc ct này nha em)
Bài tập ví dụ: Các con lắc đơn có chiều dài lần lượt là l1,l2,l3= l1+ l2,l4=l1-l2 dao động với chu kỳ
T1,T2,T3=2,4s,T4=0,8s. Tính chiều dài của con lắc 1 và 2.
Giải: l3= l1+ l2Æ (T3)2=(T1)2+(T2)2Æ5,76=(T1)2+(T2)2 (1)
l
4=l1-l2 Æ(T4)2=(T1)2-(T2)2 Æ0,64=(T1)2-(T2)2 (2)
Giải hệ ta được: (T1)2=3,2 Æ1
2
4l
g
π
=3,2Æl1=0,8m
(T2)2=2,56Æl2=0,64m
II.Sự phụ thuộc của chu kỳ vào điều kiện tự nhiên
Nếu thay đổi chỉ một trong các yếu tố :
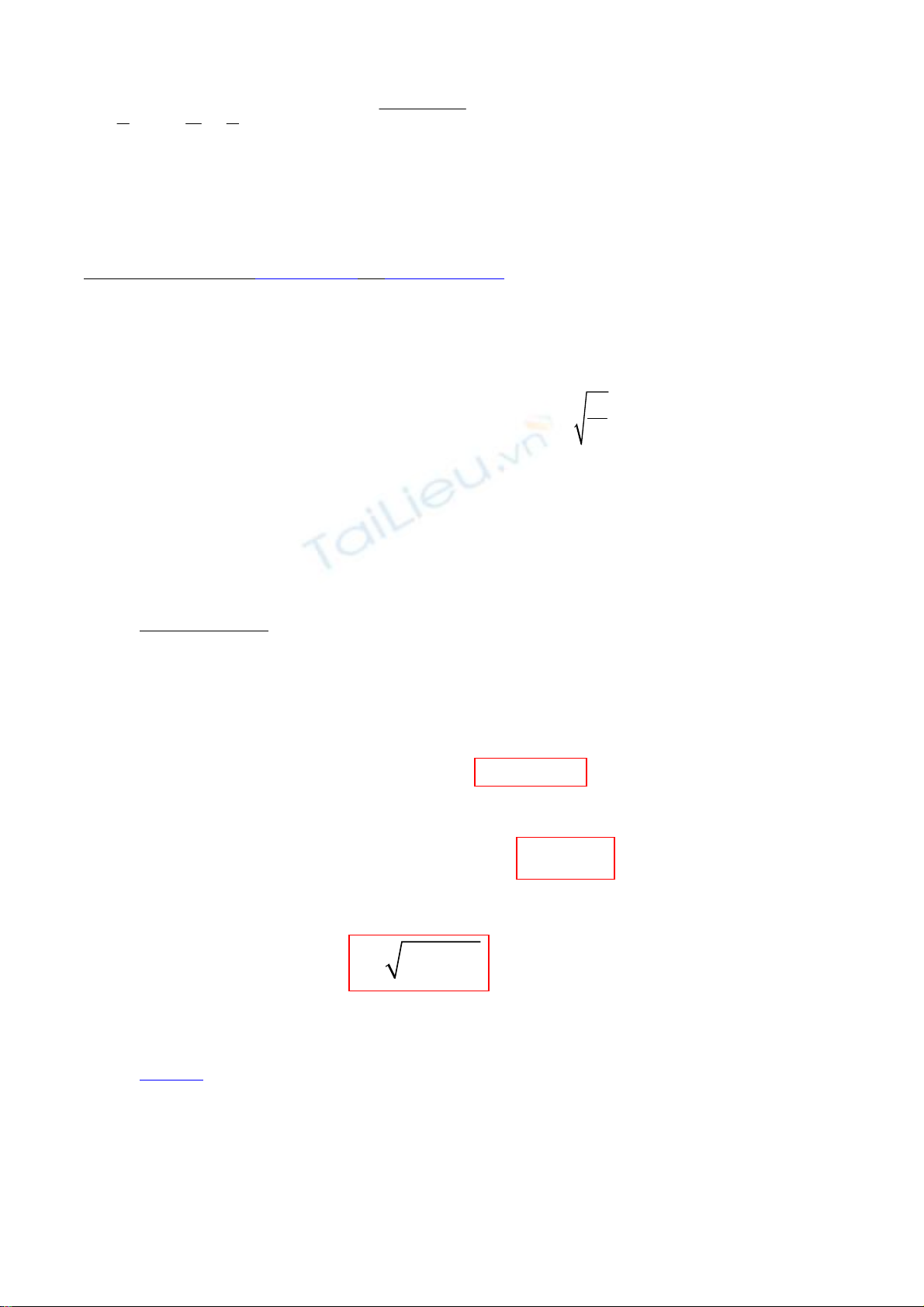
Trước tiên ta kí hiệu: θ =
1
T
T
Δ
= 21
1
TT
T
−
(độ biến thiên tỷ đối)
1. khi thay đổi nhiệt độ t: θ = 1
2αΔt
• α – hệ số nở dài của kim loại làm thanh treo
Havemind
2
Present to trang ----------------------------
havemind
• Δt - độ chênh lệch nhiệt độ (đừng nhầm thời gian) Δt = t2 - t1
2. khi đưa lên độ cao h: θ = h
R
h : là độ cao của vật so với độ cao mà đồng hồ chạy đúng( h = h2- h1 , tại h1 đồng hồ chạy đúng)
ta có thể gọi h là sự chênh lệch về độ cao.
R = 6400km (bán kính trái đất)
3. Khi đưa đến 1 nơi khác (g thay đổi): θ =
12
g
g
Δ
−
Δg = g2- g1
Lưu ý:
*.Số giây đ.hồ chạy chậm ( nhanh) trong t giây:
θ người ta còn gọi là số dây đ.hồ chạy chậm(nhanh) trong 1 s
Đề bài hỏi đ.hồ chạy nhanh(chậm) trong t giây thi ta chỉ việc lấy θ nhân với t
*.Khi nào đ.hồ chạy chậm, khi nào thì chạy nhanh?
θ>0: thì đ.hồ chạy chậm
θ<0: thì đ.hồ chạy nhanh
*.
Khi thay đổi nhiều yếu tố cùng 1 lúc:
Trong trường hợp nhiều yếu tố làm ảnh hưởng tới chu kỳ vd như nhiệt độ, độ cao,…cùng ảnh hường
tới con lắc đ.hồ thì
θ = 1
2αΔt + h
R +….( thay đổi yếu tố nào thì cộng θ của yếu tố đó)
Bài tập ví dụ: Một đồng hồ đếm giây sử dụng con lắc đơn chạy đúng ở độ cao 200m, nhiệt độ 240C.
Biết dây treo con lắc có hệ số nở dài 2.10-5K-1, bán kính Trái Đất 6400km. Khi đưa đồng hồ lên cao
1km, nhiệt độ là 200C thì mỗi ngày đêm nó chạy
A. chậm 14,256 s. B. chậm 7,344 s. C. nhanh 14,256 s. D. nhanh 7,344 s
Giải: Bài này có sự thay đổi về nhiệt đọ lẫn độ cao nên:
Havemind
3
Present to trang ----------------------------
havemind
3
1000 200
6400.10
−
θ = 1
2αΔt + h
R
= 1
2.2.10-5(20 – 24) + =8,5.10-5s >0 Î đ.hồ chạy chậm
Trong 1 ngày (86400s) thì đ.hồ chạy chậm : θ.86400 = 7,344s Î B
III.Sự phụ thuộc của chu kỳ vào ngoại lực
Có 2 lực thường gặp là lưc quán tính và lực điện trường:
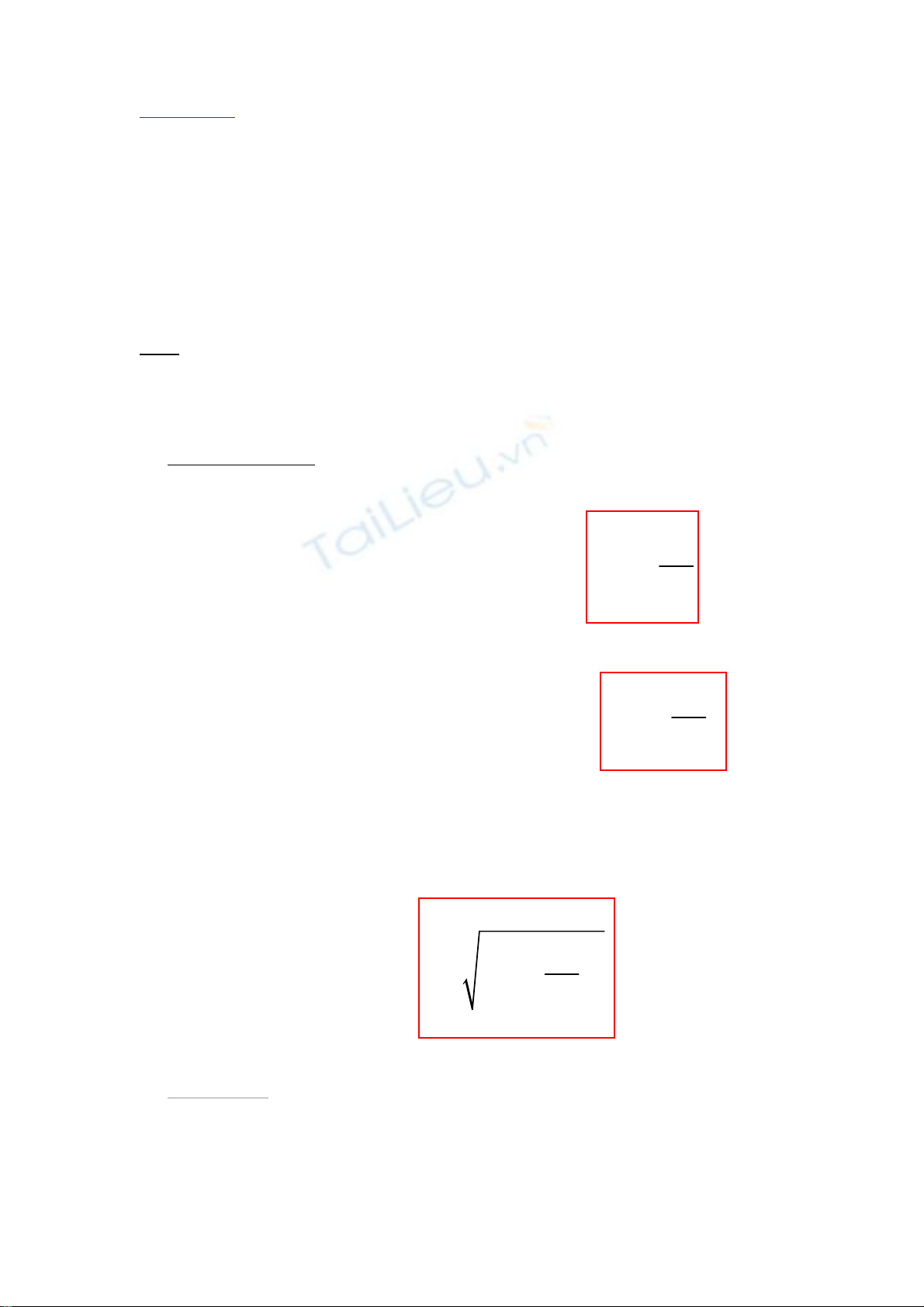
Trước tiên là phải thuộc công thức: '
mg mg=
u
ur
u
r
+ F
u
r
Trong đó: g’là gia tốc biểu kiến khi có ngoại lực tác
dụng, lúc này T’ = 2π
'
l
g
g là gia tốc trọng trường
F là ngoại lực
1. Lực quán tính: Fqt = - m.a
Trong đó a là gia tốc của vật
Dựa vào đề bài ta xác định , cùng chiều hay ngược chiều hay vuông góc với nhau: F
ur ur
g
• 2 vectơ cùng hướng: mg’=mg+ma Î g’=g + a Îg tăng Î T giảm
• 2 vectơ ngược hướng: mg’ = mg – ma Î g’ = g – a Î g giảm Î T tăng
• 2 vectơ vuông góc: g= 22
ag
+
Îg tăng Î T giảm
Lưu ý : cách xác định chiều của F
u
r
:
• Khi vật chuyển động nhanh dần đều thì Fqt hướng về phía sau(tưởng tượng chiếc xe đang
tăng tốc thì người ngồi trên xe có xu hướng hút về phía sau)
• Khi vật chuyên động chậm dần đều thì Fqt hướng về phía trước ( tưởng tượng chiếc xe
đang đi,hãm phanh thì người ngồi trên xe có xu hướng nhào về phía trước)
Havemind
4
Present to trang ----------------------------
havemind
Bài tập ví dụ: Chu kì của một con lắc đơn ở điều kiện bình thường là 1s, nếu treo nó trong
thang máy đang đi lên cao nhanh dần đều thì chu kì của nó sẽ
A. Giảm đi
B.Tăng lên
C.Không đổi
D. Có thể xảy ra cả 3 khả năng trên
Giải:
thang máy lên nhanh dần đềuÎ Fqt hướng xuốngÎFqt cùng chiều mgÎ g’=g+aÎ g tăngÎ T
giảm
2. Lực điện trường: Fđt = q.E (q có thể âm có thể dương)
Ta xét chiều của E:
• E hướng lên(ngược chiều g): mg’ = mg – qE Î g’= g - qE
m Î g giảm Î T
tăng
• E hướng xuống (cùng chiều g) : mg’ = mg + qE Î g’= g + qE
m Îg tăng Î T
giảm
• E hướng ngang (vuông góc với g):
(mg’)2 =(mg)2 + (qE)2 Î g’=
2
2qE
gm
⎛⎞
+⎜⎟
⎝⎠
Îg tăng Î T giảm
Bài tập ví dụ:1 con lắc đơn được tạo thành bằng 1 sợi dây có khối lượng không đáng kể,
đầu dây treo 1 hòn bi có khối lượng 0,01kg và mang điện tích q=2.10^-7.C. Đặt con lắc
đơn trong 1 điện trường đều có phương thẳng đứng hướng xuống dưới.Chu kỳ của con lắc
đon khi cường độ điện trường E=0 là T=2s. Tìm chu kỳ của con lắc đơn khi
E=10^4V/m.cho g=10.
Havemind
5