- 1 -
BÀI GI NG S : 10Ả Ố
N Đ NH C A THANH TH NG CH U NÉNỔ Ị Ủ Ẳ Ị
1 - M C ĐÍCH:Ụ
Gi i thi u kháí ni m v n đ nh, ph ng pháp tính toán l c t i h n c athanhớ ệ ệ ề ổ ị ươ ự ớ ạ ủ
ch u nén d c.ị ọ
2 - YÊU C U:Ầ
N m khái ni m, xây d ng bài toán -le, công th c Iasinki áp d ng đ gi iắ ệ ự Ơ ứ ụ ể ả
nh ng bài toán c th .ữ ụ ể
3 - TH I GIAN:Ờ
04 Ti t ( Lý thuy t: 02 ti t, Bài t p: 02 ti t)ế ế ế ậ ế
4 - VAÄT CHAÁT ÑAÛM BAÛO:
•Phoøng hoïc vaø caùc thieát bò giaûng daïy keøm theo.
•Baøi giaûng, baûng bieåu neáu coù.
•Taøi lieäu tham khaûo :
[1] Leâ Hoaøng Tuaán- Buøi Coâng Thaønh. Söùc beàn vaät lieäu
T1, T2. NXB KH&KT-1998.
[2] Buøi Troïng Löïu- Nguyeãn Vaên Vöôïng. Baøi taäp SBVL. NXB
Giaùo duïc-1996.
5 - PHÖÔNG PHAÙP TIEÁP CAÄN:
a) Giôø lyù thuyeát :
•Giaûng vieân : Chæ daån taøi lieäu nghieân cöùu vaø dieãn
ñaït nhöõng ñieàu caàn chuù yù.
• Hoïc vieân : Chuù yù nghe vaø ghi nhöõng ñieàu caàn
thieát.
b) Giôø baøi taäp :
Giaûng vieân : Toå chöùc kieåm tra 15 phuùt, gôïi yù, giaûi
ñaùp thaéc maéc, ra baøi taäp.
Hoïc vieân : Laøm baøi kieåm tra vaø töï giaûi quyeát baøi
taäp.
c) Giôø thöïc haønh :
Giaûng vieân : Höôùng daãn toùm taét, laøm thí nghieäm
maåu, phaân nhoùm.
- 2 -
Hoïc vieân : Nghieân cöùu phöông phaùp, thöïc haønh thí
nghieäm döôùi söï giaùm saùt cuûa TNV, vieát baùo caùo thu
hoaïch.
d) Noäi dung – phöông phaùp cuï theå :
I. KHÁI NI M V N Đ NHỆ Ề Ổ Ị
Th i gian: 15 phút.ờ
Ph ng pháp: Thuy t trình.ươ ế
Trong bài m đ u, chúng ta đã nói đ n nhi m v c a môn S c b n v t li u làở ầ ế ệ ụ ủ ứ ề ậ ệ
tính toán đ b n, đ c ng và đ n đ nh c a b ph n công trình hay chi ti t máyộ ề ộ ứ ộ ổ ị ủ ộ ậ ế
d i tác d ng c a các nguyên nhân bên ngoài. Các bài tr c chúng ta đã kh o sátướ ụ ủ ướ ả
cách tính đ b n và đ c ng c a thanh (hay h thanh) v i các d ng ch u l c khácộ ề ộ ứ ủ ệ ớ ạ ị ự
nhau. Bài này chúng ta s nghiên c u lý thuy t v s n đ nh c a thanh th ng ch uẽ ứ ế ề ự ổ ị ủ ẳ ị
nén đúng tâm.
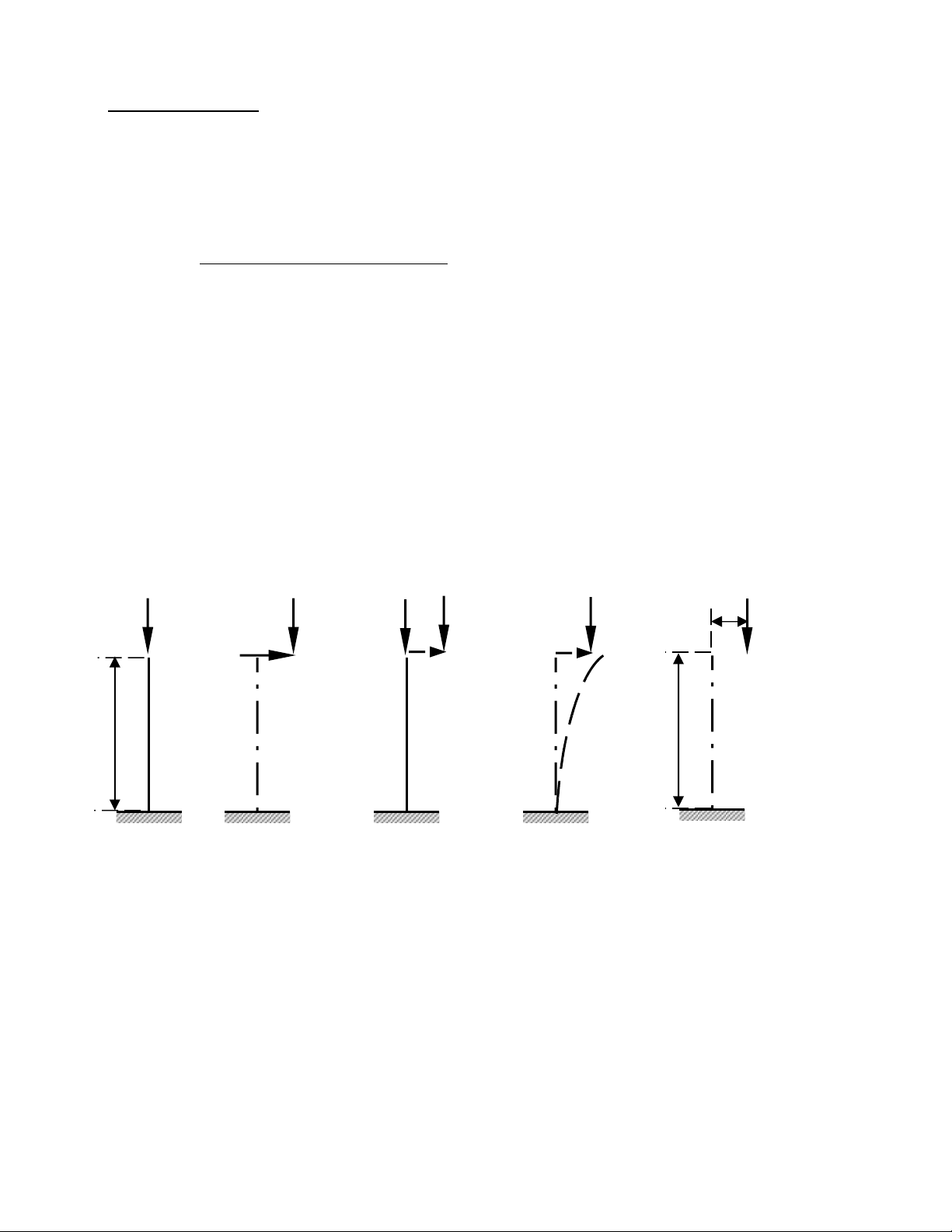
Ta có th xét s ch u l c nén đúng tâm c a m t thanh dài và m nh (Hình10-ể ự ị ự ủ ộ ả
1)đ có khái ni m v s n đ nh c a m t h đàn h i. Trên thanh tăng d n giá trể ệ ề ự ổ ị ủ ộ ệ ồ ầ ị
c a l c P ta th y hi n t ng sau: ủ ự ấ ệ ượ
−Khi P còn nh thanh ch u nén đúng tâm; n u ta tác d ng m t l c R r t nhỏ ị ế ụ ộ ự ấ ỏ
thì thanh b cong đi m t chút. Nh ng n u b l c R đi thì thanh ch v v trí banị ộ ư ế ỏ ự ở ề ị
đ u, nó v n ch u nén đúng tâm. Thanh tr ng thái cân b ng n đ nh.(Hình 10 -1c).ầ ẫ ị ở ạ ằ ổ ị
−N u tăng d n P lên đ n m t giá tr nào đó thanh v n th ng. Nh ng n u taế ầ ế ộ ị ẫ ẳ ư ế
tác d ng l c ngang R thì khi b l c R đi thanh b cong v m t phía mà không tr vụ ự ỏ ự ị ề ộ ở ề
tr ng thái ban đ u đ c. Khi đó thanh tr ng thái t i h n. Tr s l c P ng v iạ ầ ượ ở ạ ớ ạ ị ố ự ứ ớ
tr ng thái t i h n g i là l c t i h n Pạ ớ ạ ọ ự ớ ạ th.(Hình 10 -1d).
−N u tăng P l n h n Pế ớ ơ th thì thanh cong r t nhanh và r b phá ho i đ t ng t.ấ ễ ị ạ ộ ộ
Hình 10-1
P
L
a)
P
R
b)
P<Pt
R
c)
P=Pt
R
d)
P>P
f
e)
L
- 3 -
Khi đó thanh tr ng thái m t n đ nh, bi n d ng tăng khá nhanh.(Hình10 -1e). Quaở ạ ấ ổ ị ế ạ
th c nghi m ta th y khi: ự ệ ấ
P = 1,010 Pth thì f = 9 % L
P = 1,015 Pth thì f = 22% L
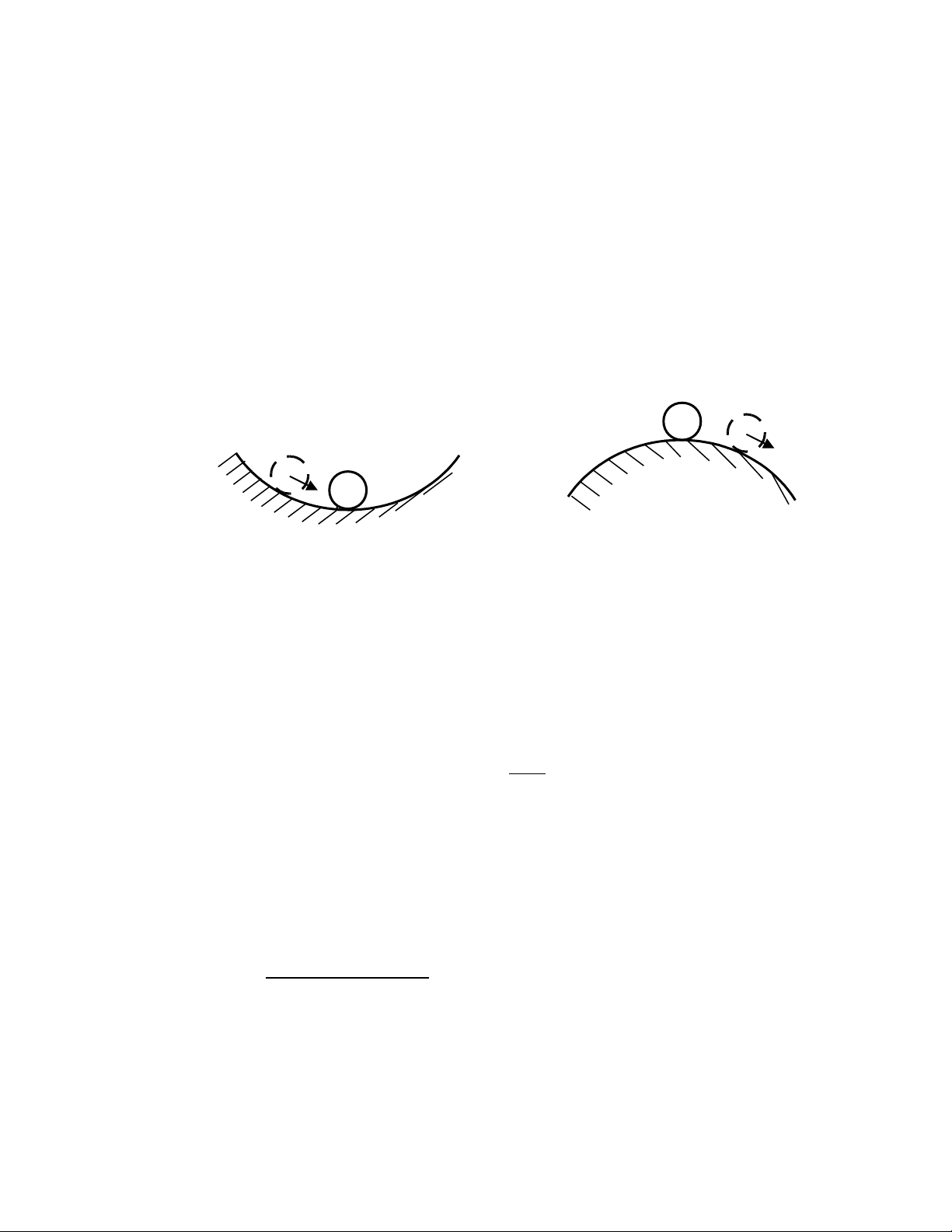
S phân tích trên đ i v i thanh có th so sánh v i s cân b ng c a v t r n hìnhự ố ớ ể ớ ự ằ ủ ậ ắ
c u đ t trên m t lõm hay m t l i (Hình 10 -2). ầ ặ ặ ặ ồ
−N u hình c u đ c đ t trên m t lõm v trí th p nh t (Hình 10-2a) thìế ầ ượ ặ ặ ở ị ấ ấ
n uế
đ y nó ra kh i v trí cân b ng này nó l i tr v ngay v trí cân b ng khi b l c đ yẩ ỏ ị ằ ạ ở ề ị ằ ỏ ự ẩ
đi. Hình c u v trí cân b ng n đ nh (nh thanh ch u l c P < Pầ ở ị ằ ổ ị ư ị ự th)
−N u đ hình c u trên m t l i v trí cao nh t thì n u không có l c đ yế ể ầ ặ ồ ở ị ấ ế ự ẩ
ngang nó s cân b ng t i v trí này, nh ng n u có l c đ y ngang nó r i kh i v tríẽ ằ ạ ị ư ế ự ẩ ờ ỏ ị
cân b ng và không th tr v v trí ban đ u đ c n a. Hình c u v trí cân b ngằ ể ở ề ị ầ ượ ữ ầ ở ị ằ
không n đ nh (nh thanh ch u l c Pổ ị ư ị ự ≥ Pth).
Trong th c t ta th y m t s hi n t ng m t n đ nh khác c a h đàn h i nhự ế ấ ộ ố ệ ượ ấ ổ ị ủ ệ ồ ư
d m công son ch u l c, ng tròn ch u áp l c phân b đ u vv… Nh v y khi tínhầ ị ự ố ị ự ố ề ư ậ
toán, thi t k ta ph i tính đ n c s m t n đ nh c a công trình hay chi ti t máy,ế ế ả ế ả ự ấ ổ ị ủ ế
t c là t i tr ng tính toán ph i nh h n t i tr ng cho phép v m t n đ nh. C th :ứ ả ọ ả ỏ ơ ả ọ ề ặ ổ ị ụ ể
P ≤
od
th
K
P
đây: PỞth là l c t i h n đ c tính toán theo các kêt c u c th .ự ớ ạ ượ ấ ụ ể
Kođ là h s an toàn v n đ nh.ệ ố ề ổ ị
P là l c tác d ng lên k t c uự ụ ế ấ
Nh v y đ gi i đ c bài toán v n đ nh, c b n là xác đ nh đ c l c t iư ậ ể ả ượ ề ổ ị ơ ả ị ượ ự ớ
h n.ạ
II. BÀI TOÁN -LEƠ
Th i gian: 35 phútờ
Ph ng pháp: Thuy t trình, di n gi iươ ế ễ ả
1 - Xác đ nh l c gi i h n c a thanh ch u nén đúng tâmị ự ớ ạ ủ ị
a)
b)
Hì nh
10- 2
- 4 -
Bây gi ta xác đ nh l c t i h n c a thanh ch u nén đúng tâm. Đây là tr ng h pờ ị ự ớ ạ ủ ị ườ ợ
m t n đ nh th ng g p nh t trong k thu t. Bài toán này đ c -le gi i nămấ ổ ị ườ ặ ấ ỹ ậ ượ Ơ ả
1774.
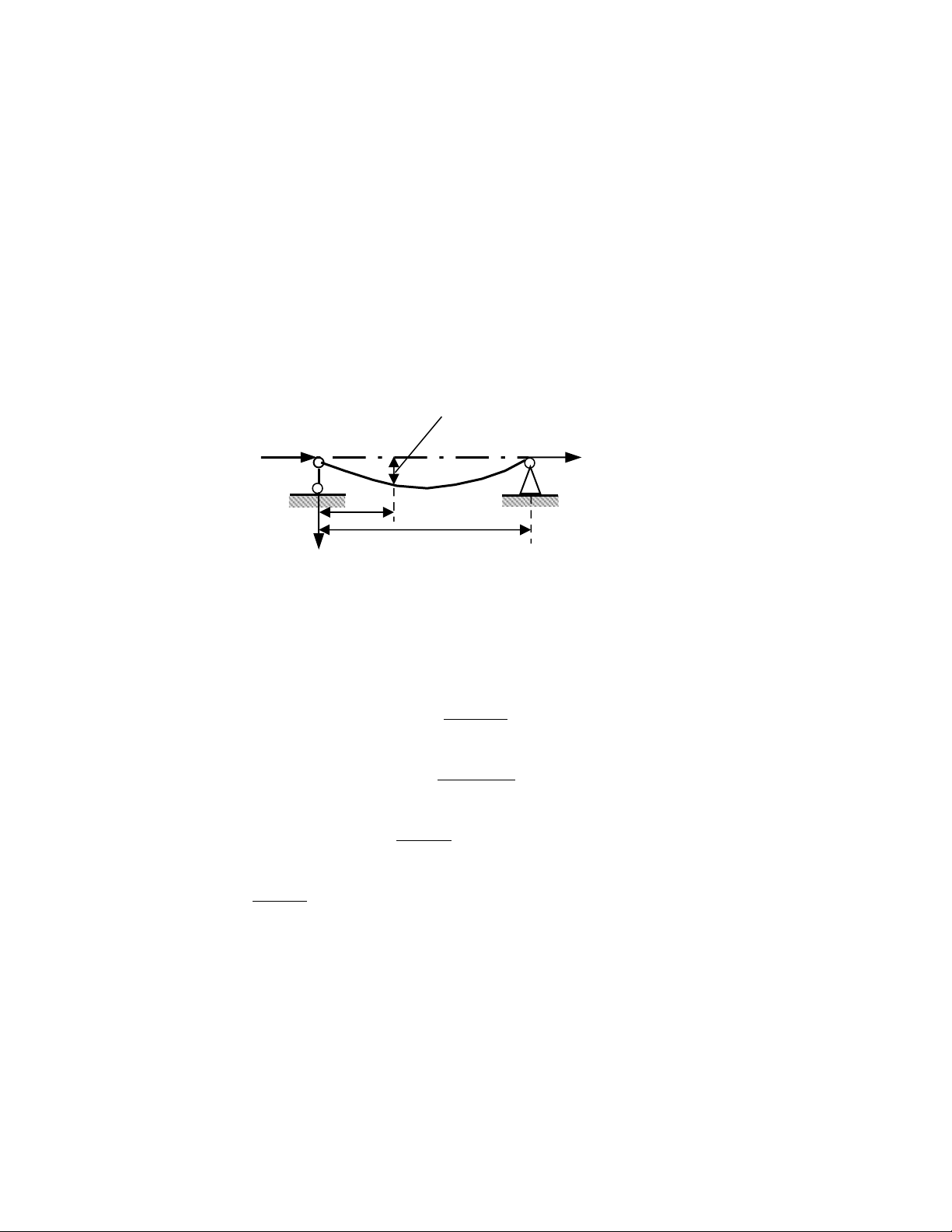
Xét thanh th ng m t c t ngang không đ i liên k t kh p v i 2 đ u, ch u l c nénẳ ặ ắ ổ ế ớ ớ ầ ị ự
đúng tâm P (Hình 10-3). Khi đ t đ n l c t i h n Pạ ế ự ớ ạ th thanh s có d ng cong nào đó.ẽ ạ
Th c t cho th y n u liên k t 2 đ u là kh p c u thì thanh s cong trong m tự ế ấ ế ế ở ầ ớ ầ ẽ ặ
ph ng có đ c ng bé nh t. Bây gi ta xác đ nh l c t i h n đó.ẳ ộ ứ ấ ờ ị ự ớ ạ
V i h tr c (nh hình v ) trong m t ph ng có đ c ng nh , t i m t c t có toớ ệ ụ ư ẽ ặ ẳ ộ ứ ỏ ạ ặ ắ ạ
đ z thanh có đ cong là y(z). B qua tr ng l ng b n thân c a thanh thì n i l cộ ộ ỏ ọ ượ ả ủ ộ ự
trên m t c t là Mômen u n:ặ ắ ố
Mz = Pth × y(z) (a)
Ta gi thi t r ng khi m t n đ nh thanh v n làm vi c trong gi i h n đàn h i.ả ế ằ ấ ổ ị ẫ ệ ớ ạ ồ
Do đó ta s d ng đ c ph ng trình vi phân g n đúng đ ng đàn h i. đây thanhử ụ ượ ươ ầ ườ ồ Ở
b u n trong m t ph ng có đ c ng nh nh t, nên ph ng trình có d ng:ị ố ặ ẳ ộ ứ ỏ ấ ươ ạ
(b)
Thay (a) vào (b) ta có:
min
th
JE
)z(yP
)z(y ⋅
⋅
−=
′′
hay:
0)z(y
J.E
P
)z(y
min
th =×+
′′
(c)
Ta đ t : ặα2 =
min
th
J.E
p
(d) thì ph ng trình (c) s có d ng: y”(z) + ươ ẽ ạ α2.y(z) = 0.
Đây là ph ng trình vi phân tuy n tính thu n nh t c p 2; nghi m c a nó có d ng:ươ ế ầ ấ ấ ệ ủ ạ
y(z) = C1sinα.z + C2cosα.z (*)
Khi m t n đ nh thanh b cong đi nên y(z) không th đ ng nh t b ng 0 và d aấ ổ ị ị ể ồ ấ ằ ự
vào đi u ki n biên: Khi z = 0 thì y(z) = 0 (1)ề ệ
Khi z = L thì y(L) = 0 (2)
T đi u ki n (1) ta tìm đ c Cừ ề ệ ượ 2 = 0, lúc này ph ng trình có d ng:ươ ạ
y(z) = C1sinα.z = 0
T đi u ki n (2) ta có: y(L) = Cừ ề ệ 1sinα.L = 0
L
y(z
)
y
z
z
P
Hì nh 10-
4
- 5 -
N u Cế1 = 0 thì y(z) = 0 thanh luôn luôn th ng. Đi u này trái v i gi thi t. ẳ ề ớ ả ế
Vì v y: sinậα.L = 0 => α.L = n.π (n = 1, 2, 3,…) => α =
L
.n π
(**)
Nh v y đ ng đàn h i có d ng v i ph ng trình:ư ậ ườ ồ ạ ớ ươ
z
L
.n
sin.C)z(y
1
⋅
π
=
(10 -1)
Thay (**) vào (d) ta tính đ c l c t i h n sau:ượ ự ớ ạ
(10 -2)
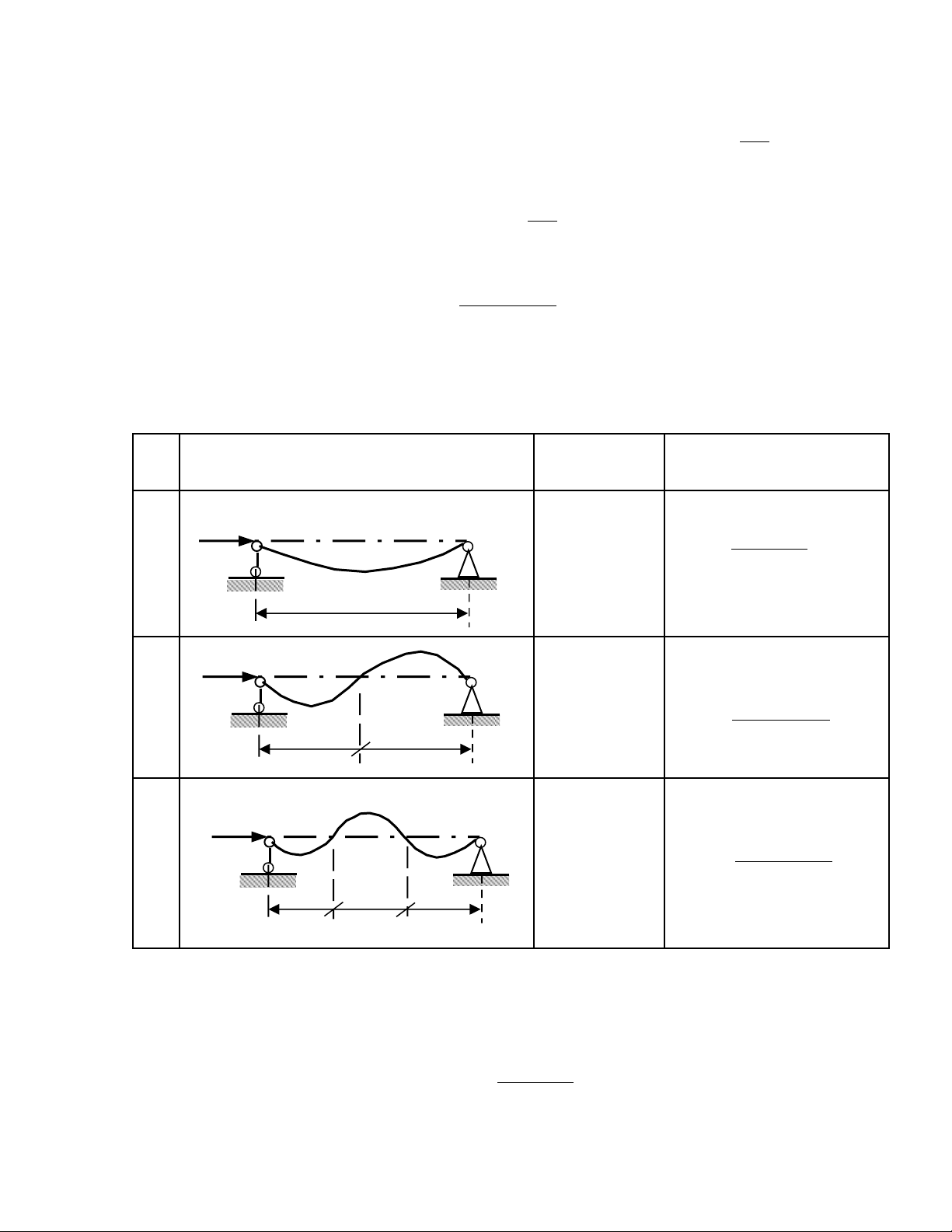
V i nh ng tr s n khác nhau thì l c t i h n có nh ng tr s khác nhau ng v iớ ữ ị ố ự ớ ạ ữ ị ố ứ ớ
các d ng đ ng đàn h i khác nhau. B ng 10-1 gi i thi u m t s tr ng h p v i nạ ườ ồ ả ớ ệ ộ ố ườ ợ ớ
= 1, 2, 3.
B ng 10-1ả
nHình dáng thanh khi m t n đ nhấ ổ ị S n aố ử
b c sóngướ L c t i h nự ớ ạ
1
1
2
min
2
L
J.Eπ
2
2
2
min
22
L
J.E2 π
3
3
2
min
22
L
J.E3 π
Trong th c t bao gi l c cũng tăng d n t 0 đ n m t giá tr nh t đ nh; nên ch ự ế ờ ự ầ ừ ế ộ ị ấ ị ỉ
c n P đ t t i giá tr nh nh t trong b ng 10-1 ( ng v i n = 1) là thanh đã m t nầ ạ ớ ị ỏ ấ ả ứ ớ ấ ổ
đ nh. Nh v y l c t i h n đ i v i thanh ch u nén đúng tâm có liên k t kh p haiị ư ậ ự ớ ạ ố ớ ị ế ớ ở
đ u là:ầ
2
min
2
th
L
J.E
Pπ
=
(10 -3)
L
P
L/
2
P
L/
2
L/
3
P
L/
3
L/
3