Ôn thi học kì 1 Đại số lớp 9: Căn thức và Rút gọn biểu thức

Chia sẻ: Nhi Nhi | Ngày: | Loại File: PDF | Số trang:9

Thêm vào BST

Báo xấu

182
lượt xem 27
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Tài liệu ôn thi học kì 1 môn Đại số lớp 9 có lý thuyết và ví dụ minh họa giúp dễ hình dung, hy vọng tài liệu sẽ giúp ích được cho các bạn học sinh lớp 9 trong kì thi sắp tới nhé.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Ôn thi học kì 1 Đại số lớp 9: Căn thức và Rút gọn biểu thức

N THI HỌC KỲ 1 – ẠI SỐ CHỦ Ề 1: CN THỨC – RT GỌN BIỂU THỨC I. CN THỨC:  Kiến thức c bản: 1. iều kiện tồn tại : A C ngha A 0 2. Hằng ẳng thức: A2 A 3. Lin hệ giữa php nhn v php khai phng: A.B A. B (A 0; B 0) A A 4. Lin hệ giữa php chia v php khai phng: (A 0; B 0) B B 5. a thừa số ra ngoi cn: A 2 .B A B. (B 0) 6. a thừa số vo trong cn: A B A 2 .B (A 0; B A B A 2 .B (A A A.B 7. Khử cn thức ở mẫu: ( 0) B B C C( 8. Trục cn thức ở mẫu: A B  Bi tập:  Tm iều kiện xc ịnh: Với gi trị n  cc biểu thức sau y xc ịnh: 2 1) 2x 3 2) x2 4 5 3) 4) 2 x 3 x 6 5) 3x 4 6) 1 x 2 3 3 7) 8) 1 2x 3x 5  Rỳt gọn biểu thức 1) 12 5 3 48 2) 5 5 20 3 45 3) 2 32 4 8 5 18 4) 3 12 4 27 5 48 5) 12 75 27 6) 2 18 7 2 162 7) 3 20 2 45 4 5 8) ( 2 2) 2 2 2 1 1 1 1 9) 10) 5 1 5 1 5 2 5 2 2 2 2 2 11) 12) 4 3 2 4 3 2 1 2 13) ( 28 2 14 7) 7 7 8 14) ( 14 3 2 ) 2 6 28 2 2 15) ( 6 5) 120 16) (2 3 3 2 ) 2 6 3 24 Trang 1
17) (1 2 )2 ( 2 3) 2 18) ( 3 2) 2 ( 3 1) 2 19) ( 5 3)2 ( 5 2) 2 20) ( 19 3)( 19 3) 7 5 7 5 21) 4 x ( x 12) 2 ( x 2) 22) 7 5 7 5 23) x 2 y ( x 4 xy 4 y ) (x 2 y) 2 2 2  Giải phng trnh: 1) 2x 1 5 2) x 5 3 3) 9(x 1) 21 4) 2x 50 0 5) 3 x 2 12 0 6) (x 3)2 9 7) 4x 2 4 x 1 6 8) (2x 1) 2 3 9) 4x 2 6 10) 4(1 )2 6 0 11) 3 x 1 2 12) 3 3 2 II. CÁC BÀI TOÁN RÚT GỌN: A.CC BỚC THỰC HIN:  Phn tch tử v mẫu thnh nhn tử (rồi rt gọn nế Tm KX của biểu thức: l tm TX của từng rồi kết luận lại. Quy ồng, gồm cc bớc: + Chọn mẫu chung : l tch cc nhn tử chun ng, mỗi nhn tử lấy số m lớn nhất. + Tm nhn tử phụ: lấy mẫu chung chia cho u ể ợc nhn tử phụ tng ứng. + Nhn nhn tử phụ với tử – Giữ nguyn m hung. Bỏ ngoặc: bằng cch nhn a thức ho ng hằng ẳng thức. Thu gọn: l cộng trừ cc hạng dạng. Phn tch tử thnh nhn tử ( guyn). Rt gọn. B.BI TẬP LUYỆ x 2x x Bài 1 Cho biểu th = với ( x >0 v x ≠ 1) x 1 x x 1) Rút gọn biểu thức A. 2) Tính giá trị của biểu thức A tại x 3 2 2 a 4 a 4 4 a Bài 2. Cho biểu thức : P = ( Với a 0;a 4) a 2 2 a 1) Rút gọn biểu thức P. 2) Tìm giá trị của a sao cho P = a + 1. x 1 2 x x x Bài 3: Cho biểu thức A = x 1 x 1 1/.ặt iều kiện ể biểu thức A c ngha 2/.Rút gọn biểu thức A Trang 2
3/.Với gi trị no của x th A< -1 x x x x Bài 4: Cho biểu thức A = (1 )(1 ) ( Với x 0; x 1 ) x 1 x 1 a) Rút gọn A b) Tìm x ể A = - 1 1 1 x Bài 5: Cho biểu thức : B = 2 x 2 2 x 2 1 x a; Tm TX rồi rt gọn biểu thức B b; Tnh gi trị của B với x =3 1 c; Tm gi trị của x ể A 2 x 2 x 2 x Bài 6: Cho biểu thức : P = x 2 x 2 4 x a; Tm TX b; Rt gọn P c; Tm x ể P = 2 1 1 a 1 Bài 7: Cho biểu thức: Q=( ) :( a 1 a a a; Tm TX rồi rt gọn Q b; Tm a ể Q dng c; Tnh gi trị của Biểu thức biết a = 9- 4 a 1 a a Bài 8: Cho biểu thức: M = 2 2 a a a/ Tm KX của M. b/ Rt gọn M Tm gi trị của a ể CHỦ Ề 2: M SỐ - HM SỐ BẬC NHẤT I. HM SỐ: Khi niệm hm số * Nếu ại lợng y phụ thuộc vo ại lợng x sao cho mỗi gi trị của x, ta lun xc ịnh ợc chỉ một gi trị tng ứng của y th y ợc gọi l hm số của x v x ợc gọi l biến số. * Hm số c thể cho bởi cng thức hoặc cho bởi bảng. II. HM SỐ BẬC NHẤT:  Kiến thức c bản:  ịnh ngha: Hm số bậc nhất c dạng: y ax b Trong  a; b l cc hệ số a 0 Nh vậy: iều kiện ể hm số dạng: y ax b l hm số bậc nhất l: a 0 V dụ: Cho hm số: y = (3 – m) x - 2 (1) Tm cc gi trị của m ể hm số (1) l hm số bậc nhất. Trang 3
Giải: Hm số (1) l bậc nhất 3 m 0 0 3  Tnh chất: + TX: x R + ồng biến khi a 0 . Nghịch biến khi a 0 V dụ: Cho hm số: y = (3 – m) x - 2 (2) Tm cc gi trị của m ể hm số (2): + ồng biến trn R + Nghịch biến trn R Giải: + Hm số (1) ồng biến 3 m 0 0 3 + Hm số (1) Nghịch biến 3 m 0 0 3  ồ thị: + ặc iểm: ồ thị hm số bậc nhất l ờng thẳng cắt trục tung tại iểm c tung ộ bằngb. b cắt trục honh tại iểm c honh ộ bằng . 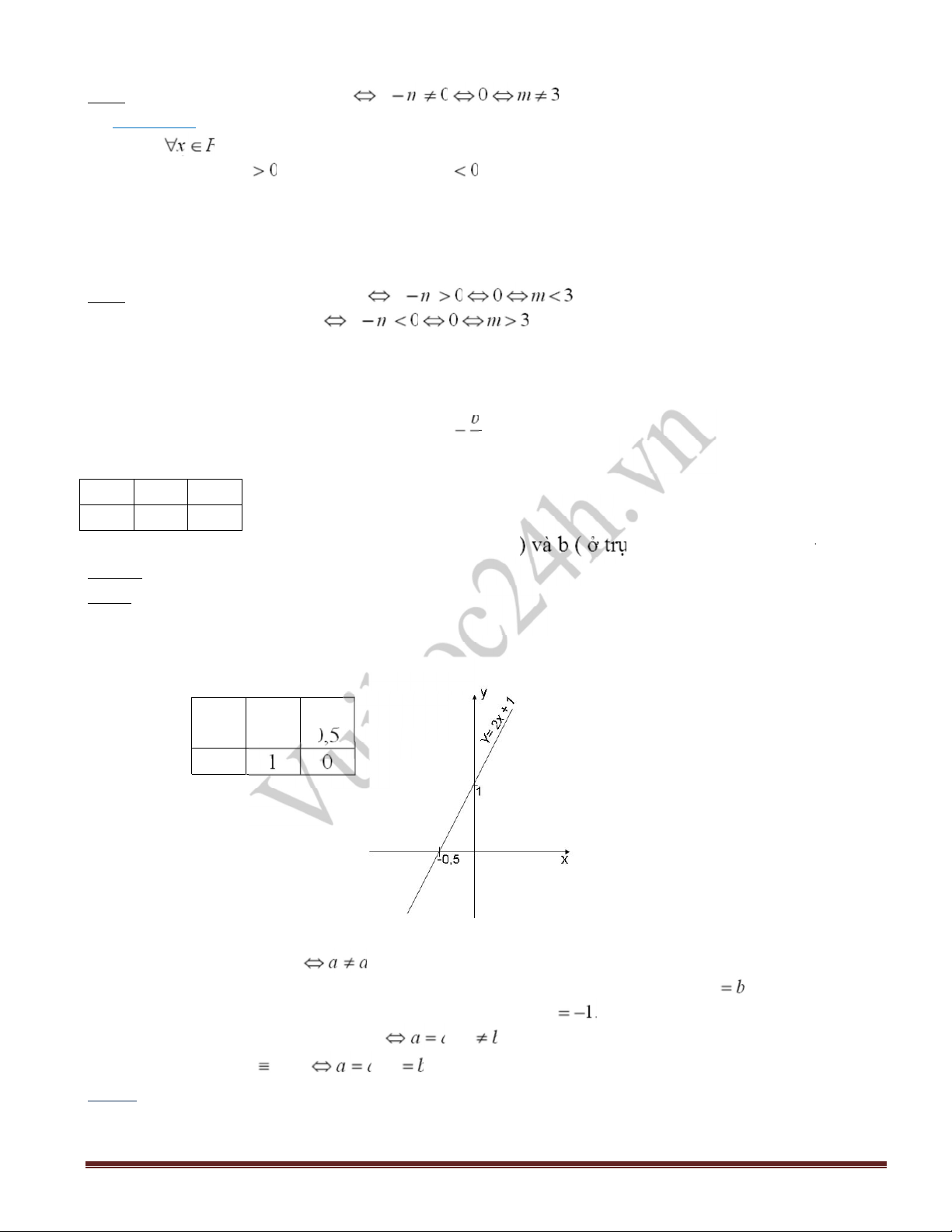a + Từ ặc iểm  ta c cch vẽ: x 0 -b/a y b 0 Vẽ ờng thẳng qua hai iểm: -b/a ( ở trục honh) ục tung) V dụ: Vẽ ồ thị hm số : y = 2x + 1 Giải: - x 0 05 y  iều kiện ể hai ờng thẳng: (d1): y = ax + b; (d2): y = a,x + b, : + Cắt nhau: (d1) cắt (d2) a a , . */. ể hai ờng thẳng cắt nhau trn trục tung th cn thm iều kiện b b ' . */. ể hai ờng thẳng vung gc với nhau th : a.a ' 1. + Song song với nhau: (d1) // (d2) a a , ; b b ' . + Trùng nhau: (d1) (d2) a a , ;b b ' . V dụ:Cho hai hm số bậc nhất:y = (3–m)x+ 2 (d1) và y=2x–m(d2 ) a/ Tm gi trị của m ể ồ thị hai hm số song song với nhau. Trang 4
b/ Tm gi trị của m ể ồ thị hai hm số cắt nhau c/ Tm gi trị của m ể ồ thị hai hm số cắt nhau tại một iểm trn trục tung. Giải: 3 m 2 m 1 a/ (d1)//(d2 ) m 1 2 m m 2 b/ (d1) cắt (d2) 3 m 2 1 c/ (d1) cắt (d2) tại một iểm trn trục tung m 2 2  Hệ số gc của ờng thẳng y = ax + b là a. + Cch tnh gc tạo bởi ờng thẳng với trục Ox l dựa vo tỉ số lợng gic tg a Trờng hợp: a > 0 th gc tạo bởi ờng thẳng với trục Ox l gc nhọn. Trờng hợp: a < 0 th gc tạo bởi ờng thẳng với trục Ox l gc t ( 1800 ) V dụ 1: Tnh gc tạo bởi ờng thẳng y = 2x + 1 với trục Ox Giải: Ta có: Tan 2 630 Vậy gc tạo bởi ờng thẳng y = 2x + i trục Ox l: 630. 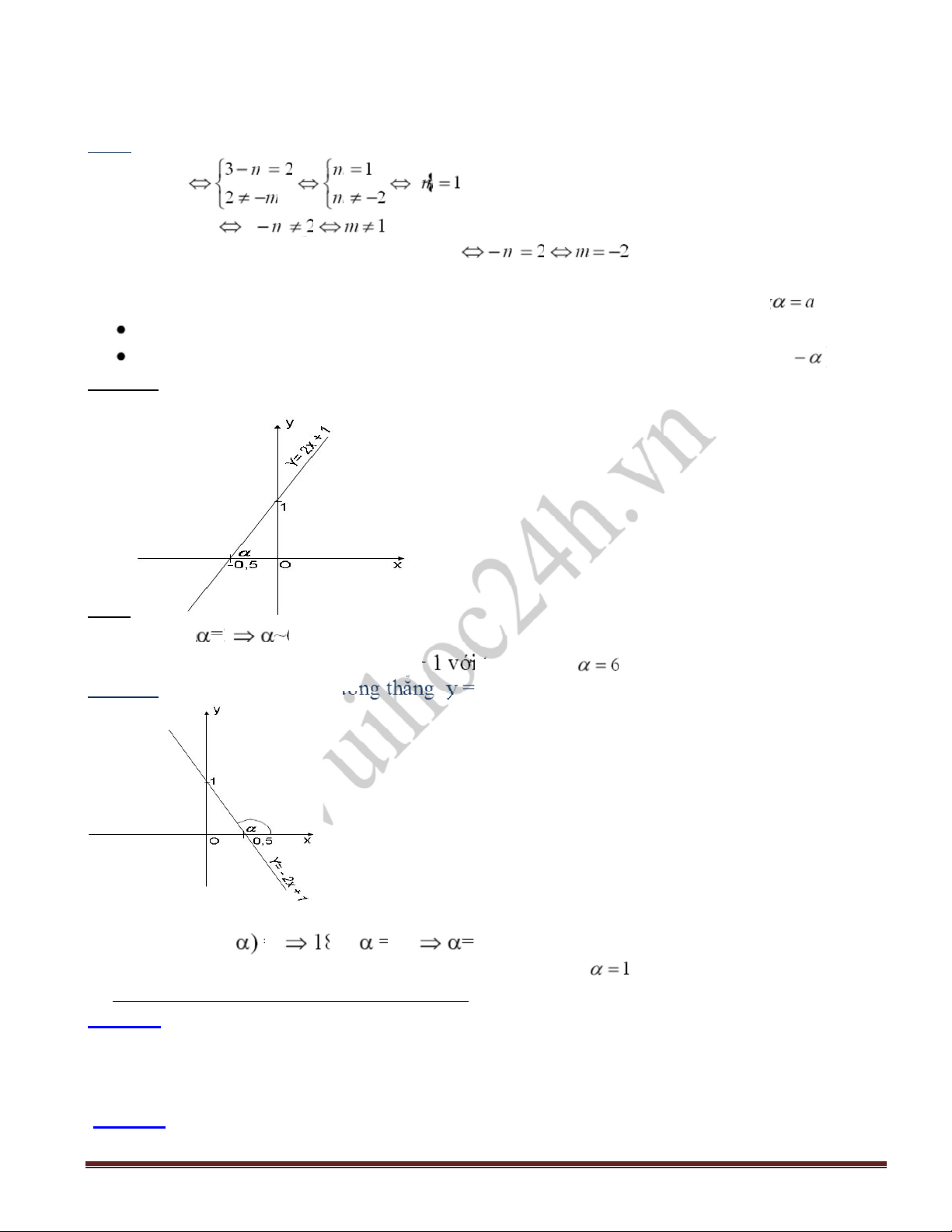V dụ 2: Tnh gc tạo bởi ờn y - 2x + 1 với trục Ox. Ta có: Tan(1800- =2 800- =630 1170 Vậy gc tạo bởi ờng thẳng y = - 2x + 1 với trục Ox l: 1170.  CC DẠNG BI TẬP THỜNG GẶP: - Dạng1: Xc dịnh cc gi trị của cc hệ số ể hm số ồng biến, nghịch biến, Hai ờng thẳng song song; cắt nhau; trựng nhau. Phng php: Xem lại cc v dụ ở trn. -Dạng 2: Vẽ ồ thị hm số y = ax + b Xem lại cc v dụ ở trn. Trang 5
Xc ịnh toạ ộ giao iểm của hai ờng thẳng (d1): y = ax + b; (d2): y = a,x + b, Phng php: ặt ax + b = a,x + b, giải phng trnh ta tm ợc gi trị của x; thay gi trị của x vo (d1) hoặc (d2) ta tnh ợc gi trị của y. Cặp gi trị của x v y l toạ ộ giao iểm của hai ờng thẳng. Tnh chu diện tch của cc hnh tạo bởi cc ờng thẳng: Phng php: +Dựa vo cc tam gic vung v ịnh l Py ta go ể tnh ộ di cc oạn thẳng khng biết trực tiếp ợc. Rồi tnh chu vi tam gic bằng cch cộng cc cạnh. + Dựa vo cng thức tnh diện tch tam gic ể tnh S -Dạng 3: Tính góc tạo bởi ờng thẳng y = ax + b v trục Ox Xem lại cc v dụ ở trn. -Dạng 4: iểm thuộc ồ thị; iểm khng thuộc ồ thị: Phng php: V dụ: Cho hm số bậc nhất: y = ax + b. iểm M (x1; y1) c thuộc ồ thị không? Thay gi trị của x1 vào hàm số; tnh ợc y0. Nếu y0 = y1 th iểm uộc ồ thị. Nếu y0 y1 th iểm M khng thuộc ồ thị. -Dạng 5: Viết phng trnh ờng thẳng: V dụ: Viết phng trnh ờng thẳng y = ax + b i qua iểm P (x0; y0) v iểm Q(x1; y1). Phng php: + Thay x0; y0 vo y = ax + b ta ợc p nh y0 = ax0 + b (1) + Thay x1; y1 vo y = ax + b ta ợ rnh y1 = ax1 + b (2) + Giải hệ phng trnh ta tm của a v b. + Thay gi trị của a v b vo y b ta ợc phng tri9nhf ờng thẳng cần tm. -Dạng 6: Chứng minh ờng thẳng i qua iểm cố ịnh hoặc chứng minh ồng quy: V dụ: Cho cc ờng thẳng : (d1) : y = (m2-1) x + m2 -5 ( Vớ m -1 ) (d2) : y = x +1 (d3) : y = -x +3 a) C/m rằng khi m lun i qua 1iểm cố ịnh . b) C/m rằng khi d1 d1 vuông góc d2 c) Xc ịnh m ể 3 ờng thẳng d1 ;d2 ;d3 ồng qui Giải: a) Gọi iểm cố ịnh m ờng thẳng d1 i qua l A(x0; y0 ) thay vào PT (d1) ta có : y0 = (m2-1 ) x0 +m2 -5 Với mọi m => m2(x0+1) -(x0 +y0 +5) =0 với mọi m ; iều ny chỉ xảy ra khi : x0+ 1 =0 x0+y0+5 = 0 suy ra : x0 =-1 Y0 = - 4 Vậy iểm cố ịnh l A (-1; - 4) b) +Ta tm giao iểm B của (d2) và (d3) : Ta c pt honh ộ : x+1 = - x +3 => x =1 Thay vo y = x +1 = 1 +1 =2 Vậy B (1;2) Trang 6
ể 3 ờng thẳng ồng qui th (d1) phải i qua iểm B nn ta thay x =1 ; y = 2 vào pt (d1) ta có: 2 = (m2 -1) .1 + m2 -5 m2 = 4 => m = 2 và m = -2 Vậy với m = 2 hoặc m = - 2 th 3 ờng thẳng trn ồng qui.  Bi tập: Bài 1: Cho hai ờng thẳng (d1): y = ( 2 + m )x + 1 và (d2): y = ( 1 + 2m)x + 2 1) Tìm m ể (d1) và (d2) cắt nhau . 2) Với m = – 1 , vẽ (d1) và (d2) trn cng mặt phẳng tọa ộ Oxy rồi tm tọa ộ giao iểm của hai ờng thẳng (d1) và (d2) bằng php tnh. Bài 2: Cho hm số bậc nhất y = (2 - a)x + a . Biết ồ thị hm số i qua iểm M(3;1), hàm số ồng biến hay nghịch biến trn R ? Vỡ sao? Bài 3: Cho hm số bậc nhất y = (1- 3m)x + m + 3 i qua N(1;-1) , hàm số ồng biến hay nghịch biến ? V sao? Bài 4: Cho hai ờng thẳng y = mx – 2 ;(m 0) và y = (2 - m) 2) . Tỡm iều kiện của m ể hai ờng thẳng trn: a) Song song. b) Cắt nhau . Bài 5: Với giỏ trị no của m th hai ờng thẳng +m v y = 3x + 5- m cắt nhau tại một iểm trn trục tung .Viết phng trn ẳng (d) biết (d) song song với 1 (d’): y = x v cắt trục honh tại iểm c h ộ bằng 10. 2 Bài 6: Viết phng trnh ờng thẳng (d) (d) song song với (d’) : y = - 2x v i qua iểm A(2;7). Bài 7: Viết phng trnh ờ qua hai iểm A(2; - 2) và B(-1;3). Bài 8: Cho hai ờng thẳng : x 2 và (d2): y = x 2 2 a/ Vẽ (d1) và (d2) tr trục tọa ộ Oxy. b/ Gọi A v B lần l ao iểm của (d1) và (d2) với trục Ox , C l giao iểm của (d1) và (d2) Tnh chu vi v diện tch của tam gic ABC (n vị trn hệ trục tọa ộ l cm)? Bài 9: Cho cc ờng thẳng (d1) : y = 4mx - (m+5) với m 0 (d2) : y = (3m2 +1) x +(m2 -9) a; Với gi trị no của m th (d1) // (d2) b; Với gi trị no của m thì (d1) cắt (d2) tm toạ ộ giao iểm Khi m = 2 c; C/m rằng khi m thay ổi th ờng thẳng (d1) lun i qua iểm cố ịnh A ;(d2) i qua iểm cố ịnh B . Tính BA ? Bài 10: Cho hm số : y = ax +b a; Xc ịnh hm số biết ồ thị của n song song với y = 2x +3 v i qua iểm A(1,-2) b; Vẽ ồ thị hm số vừa xc ịnh - Rồi tnh ộ lớn gc ạo bởi ờng thẳng trn với trục Ox ? c; Tm toạ ộ giao iểm của ờng thẳng trn với ờng thẳng y = - 4x +3 ? d; Tm gi trị của m ể ờng thẳng trn song song với ờng thẳng y = (2m-3)x +2 Trang 7
CHỦ Ề 3: HỆ HAI PHNG TRNH BẬC NHẤT HAI ẨN I. CC KHI NIỆM: Phng trnh bậc nhất hai ẩn: +Dạng: ax + by = c trong  a; b; c l cc hệ số  biết( a 0 hoặc b 0) + Một nghiệm của phng trnh l cặp số x0; y0 thỏa mn : ax0 + by0 = c + Phng trnh bậc nhất hai ẩn ax + by = c lun lun c v số nghiệm. + Tập nghiệm ợc biểu diễn bởi ờng thẳng (d): ax + by = c. Nếu a 0; b 0 th ờng a c thẳng (d) l ồ thị của hm số bậc nhất: y x . b b  Hệ hai phng trnh bậc nhất hai ẩn: x y c.(1) + Dạng: , , x y c , .(2) + Nghiệm của hệ l nghiệm chung của hai phng trnh + Nếu hai phng trnh ấy khng c nghiệm chung th ta n ệm + Quan hệ giữa số nghiệm của hệ v ờng thẳng biểu diễn tập nghiệm: -Phng trnh (1) ợc biểu diễn bởi ờng thẳng ( -Phng trnh (2) ợc biểu diễn bởi ờng thẳng *Nếu (d) cắt (d') hệ c nghiệm duy nhất *Nếu (d) song song với (d') th hệ v nghiệm *Nếu (d) trng (d') th hệ v số nghiệm. Hệ phng trnh tng ng: Hai hệ phng trnh ợc gọi l ng với nhau nếu chng c cng tập nghiệm II.PHNG PHP GIẢI HỆ TRNH: Giải hệ phng ng php thế: a) Quy tắc thế: + Bớc 1: Từ một rnh của hệ  cho, ta biểu diễn một ẩn theo ẩn kia, rồi thay vo phng trnh thứ hai ể ợc một phng trnh mới (chỉ cn 1 ẩn). + Bớc 2: Dng phng trnh mới ny ể thay thế cho phng trnh thứ hai trong hệ (ph- ng trnh thứ nhất cng thờng ợc thay thế bởi hệ thức biểu diễn một ẩn theo ẩn kia c ợc ở bớc 1). 2y .(1) V dụ: xt hệ phng trnh: x 2y 3.(2) + Bớc 1: Từ phng trnh (1) ta biểu diễn x theo y ( gọi l rt x) ta c: x 1 2 y.(*) Thay x 1 2 y.(*) vo phng trnh (2) ta ợc: 3(1 2 y) 2 y 3.(**) 2y + Bớc 2: Thế phng trnh (**)vo phng trnh hai của hệ ta c: (1 2 y) 2 y 3 b) Giải hệ : Trang 8
2y 2y 2y x (1 2 y) 2 y 3 6y 2y 3 y 0 y 0 Vậy hệ phng trnh c một nghiệm (x = 1; y = 0).  Giải hệ phng trnh bằng phng php cộng ại số: a)Quy tắc cộng ại số: + Bớc 1: Cộng hay trừ từng vế hai phng trnh của hệ của hệ phng trnh  cho ể - ợc một phng trnh mới. + Bớc 2: Dng phng trnh mới ấy thay thế cho một trong hai phng trnh của hệ (v giữ nguyn phng trnh kia) Lu : Khi cc hệ số của cng một ẩn ối nhau th ta cộng vế theo vế của hệ. Khi cc hệ số của cng một ẩn bằng nhau th ta trừ vế theo vế của hệ. Khi hệ số của cng một ẩn khng bằng nhau cng khng ối nhau th ta chọn nhn với số thch hợp ể a về hệ số của cng một ẩn ối nhau (hoặc bằng nhau).( tạm gọi l quy ồng hệ số) BI TẬP: Giải hệ phng trnh bằng phng php thế. x y 2 y m x 2y 6    x y 5 x y 4 y 2 x y 2x 3y 5 3x y 7    4x 6 y 2 5x 4 y x 2y 0 x 4y 2 x y 2x 3y 2    3x 2 y 4 2x 9 4x 6y 2 Giải hệ phng trnh bằng phng p cộng ại số x 1y x x y 8 x 2y     0 x 1y 31 x x y 0 x 2y x 2y 4 x 2y x y 2    x y 5 x y 3 x 5y 6 ặt ẩn phụ rồi g ệ phng trnh sau 1 4 1 1 2 ( x y ) ( x y) 4 x y 5 x 2 y    x y ) 2( x y) 5 1 1 1 2 3 y 5 2 y Trang 9