
Thực hiện: Đặng Minh Khâm – THCS Chu Văn An Trang 1
KINH NGHIỆM DẠY HỌC
ĐỀ TÀI:
VẬN DỤNG KIẾN THỨC HÌNH HỌC SƠ CẤP
ĐỂ ĐỊNH HƯỚNG TÌM LỜI GIẢI VÀ XÂY DỰNG ĐỀ BÀI TOÁN
BỒI DƯỠNG HỌC SINH GIỎI THCS
A. MỞ ĐẦU
1. Lý do chọn đề tài
Ton hc l mt trong nhng môn khoa hc cơ bn mang tnh tru tưng, nhưng
mô hnh ng dng ca n rt rng ri v gn gi trong mi lnh vc ca đi sng x
hi, trong khoa hc l thuyt v khoa hc ng dng. Ton hc l mt môn hc gi mt
vai trò quan trng trong sut bậc hc phổ thông. Tuy nhiên, n l mt môn hc kh,
khô khan v đòi hỏi ở mỗi hc sinh phi c mt s nỗ lc rt lớn để chim lnh nhng
tri thc cho mnh. Chnh v vậy, đi với mỗi gio viên dạy ton việc tm hiểu cu trúc
ca chương trnh, ni dung ca sch gio khoa, nắm vng phương php dạy hc, v
cơ sở tư duy để t đ tm ra nhng biện php dạy hc c hiệu qu trong việc truyền
th cc kin thc Ton hc cho hc sinh, phân tch, định hướng tm li gii là công
việc cn phi sng tạo, nghiên cu, lm thưng xuyên v khoa hc.
Dạy hc sinh hc Ton không ch l cung cp nhng kin thc cơ bn, dạy hc
sinh gii bi tập sch gio khoa, sch tham kho m điều quan trng l hnh thnh cho
hc sinh phương php chung để gii cc dạng ton, t đ giúp cc em tch cc hoạt
đng, đc lập sng tạo để dn hon thiện k năng, k xo, hon thiện nhân cch. Gii
ton l mt trong nhng vn đề trung tâm ca phương php ging dạy, bởi l việc gii
ton l mt việc m ngưi hc ln ngưi dạy thưng xuyên phi lm, đc biệt l đi
với nhng hc sinh bậc THCS th việc gii ton l hnh thc ch yu ca việc hc
ton
Qua nhiều năm ging dạy cho hc sinh THCS, đc biệt l cho hc sinh cc lớp
tạo nguồn, mt đi tưng tip cận nhiều dạng bi tập khc nhau, mc đ tư duy cao….
trong nhng dạng bi tập y cn đưc phân tch v tìm li gii phù hp trên đi tưng

Thực hiện: Đặng Minh Khâm – THCS Chu Văn An Trang 2
hc sinh trung hc cơ sở. Mt trong nhng cơ sở giúp tm li gii trong mt s dạng
toán phc tạp l sử dng kin thc ton hc sơ cp m mỗi gio viên đ đưc hc tập
v rèn luyện tại trưng sư phạm đề vận dng tm li gii trong mỗi dạng ton và sáng
tạo thêm mt s bi ton nhằm pht triển v rèn luyện kỹ năng tư duy v sng tạo ca
hc sinh. Sau mt qu trnh thc hiện, tôi chn đề tài “Vận dụng kiến thức hình học
sơ cấp để định hướng tìm lời giải và xây dựng đề toán bồi dưỡng cho học sinh
THCS” nhằm tch ly như mt kinh nghiệm dạy hc môn ton, đc biệt p dng cho
đi tưng hc sinh giỏi
2. Mục đích của đề tài
Trên cơ sở nhng kinh nghiệm ging dạy v thc tiễn hc tập ca hc sinh, tìm
ra nhng phương php gii bi ton hnh hc mt cch hiệu qu nht
Mc đch ca đề ti ny l trnh by cc ng dng ca kin thc hnh hc sơ
cp (đc biệt l mt s phép bin hnh trong mt phẳng) để định hướng tm li gii
bài ton cp trung hc cơ sở, c thể l cc bi ton chng minh, tm điểm c
định….(riêng phn quỹ tch, dng hnh không đề cập đền trong phạm vi đề ti ny).
3. Phạm vi thể nghiệm
Đề ti đưc thể nghiệm tại đơn vị công tc l trưng THCS Chu Văn An. C
thể l nhng hc sinh lớp tạo nguồn v nhng hc sinh tham gia đi tuyển hc sinh
giỏi Ton ca trưng.
4. Cơ sở thực hiện
Để thc hiện đề ti ny, tôi da trên cơ sở cc kin thc đ hc ở Trưng sư
phạm, cc ti liệu về phương php ging dạy, cc ti liệu bồi dưỡng thưng xuyên,
sch gio khoa, sch bi tập, sch tham kho… ca b môn Ton bậc trung hc cơ sở
5. Phương pháp nghiên cứu
Thc hiện đề ti ny, tôi sử dng cc phương php sau đây:
– Phương php nghiên cu lý luận
– Phương php kho st thc tiễn
– Phương php phân tch

Thực hiện: Đặng Minh Khâm – THCS Chu Văn An Trang 3
– Phương php tổng hp
– Phương php khi qut ha
– Phương php quan st
– Phương php kiểm tra
– Phương php tổng kt kinh nghiệm
6. Thời gian thực hiện
Đề ti đưc thc hiện t ngy 05/09/2013 đn ngy 30/1/2016
7. Giới hạn của đề tài
Đề ti thc hiện như nhng kinh nghiệm đưc sử dng trong việc bồi dưỡng đi
tuyển hc sinh giỏi cc cp, với đi tưng l nhng hc sinh giỏi b môn Ton. Trên
cơ sở nhng kinh nghiệm ging dạy v thc tiễn hc tập ca hc sinh, định hướng để
tm ra nhng phương php gii bi ton hnh hc mt cch hiệu qu nht.
B. NỘI DUNG
ỨNG DỤNG KIẾN THỨC HÌNH HỌC SƠ CẤP TRONG XÂY DỰNG ĐỀ
TOÁN VÀ DỰ ĐOÁN LỜI GIẢI
I. ỨNG DỤNG TRONG XÂY DỰNG ĐỀ TOÁN
Nhng kin thc trong phn hnh hc sơ cp l cơ sở v nền tng cho việc hnh
thnh phn hnh hc phẳng trong chương trnh ton THCS. T nhng kin thc đ
tch ly đưc trong qu trnh hc tập t trưng sư phạm, ngưi gio viên c thể vận
dng nhng kin thc v kinh nghiệm gii ton ny trong việc định hướng tm li gii,
xây dng nhng đề ton mới, giúp hc sinh thêm cch suy luận v phân tich tm li
gii cch hiệu qu, như cc v d minh ha sau:
1. Vận dụng kiến thức về phương tích
Phương tch l mt trong nhng ni dung ca môn hnh hc sơ cp, nhưng lại
đưc sử dng rt nhiều trong việc hnh thnh v l ni dung tiềm ẩn ri rc trong các
bi ton cp THCS đc biệt l hnh hc lớp 9. Nhng ngưi thy sử dng kin thc
này để c thể nhận ra, định hướng tm li gii hay đề ra mt s bi ton thch hp giúp
Thực hiện: Đặng Minh Khâm – THCS Chu Văn An Trang 4
hc sinh có cơ sở định hướng tm li gii, hay rèn luyện kỹ năng suy luận, c thể như
các ví d sau
V d 1: T kin thc phương tch MA.MB = MO2−r2.
Ta xây dng bài toán sau
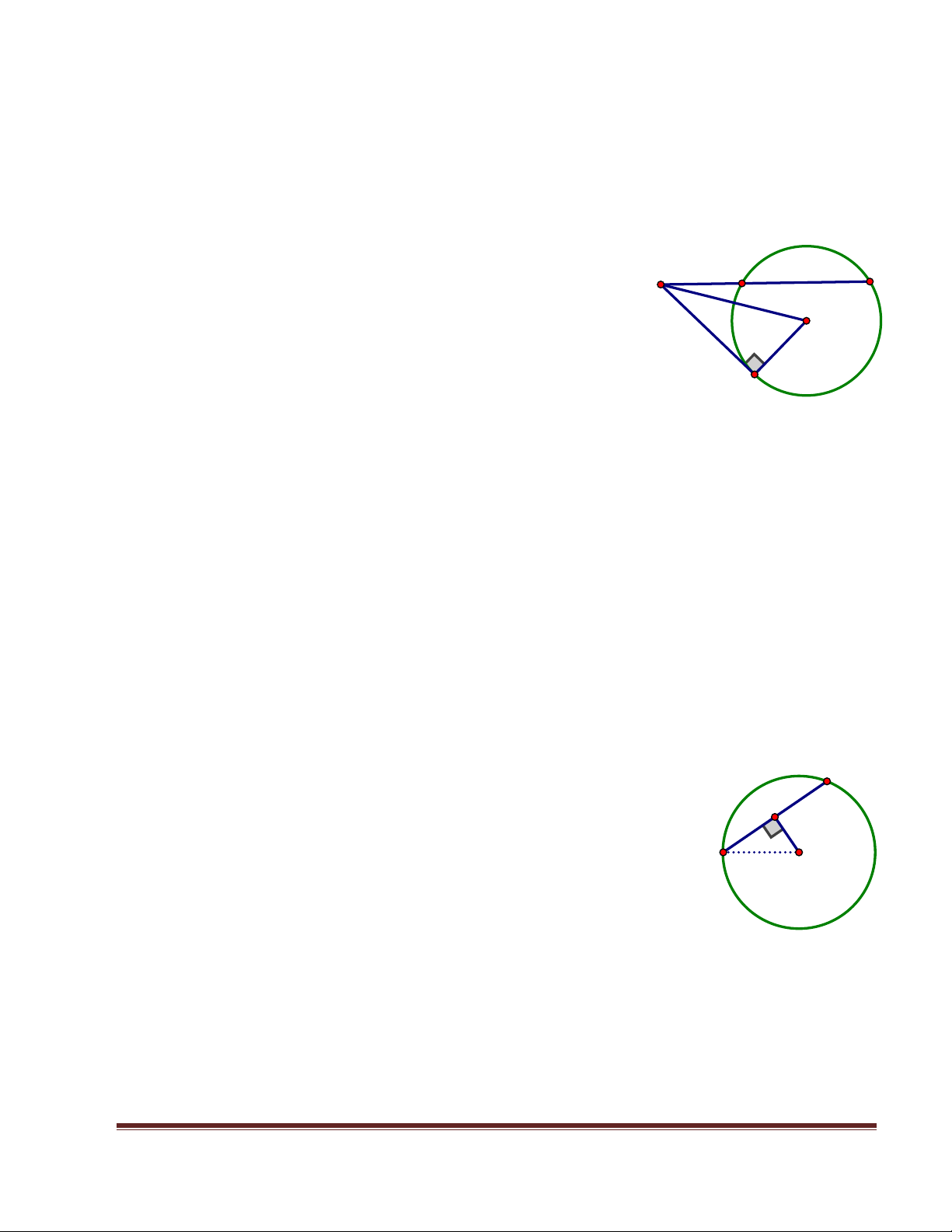
Bi 1 Cho điểm M nằm ở pha bên ngoài ca đưng
tròn (O). V đưng tip tuyn MT đn đưng tròn. V
ct tuyn MAB Chng minh MA.MB=MT2=MO2−r2.
HD: Hc sinh dễ dng : Sử dng định lý Pi-ta-go để
chng minh : MT2=MO2−r2 ( M nằm ngoi đưng tròn)
Sử dng tam gic đồng dạng MAT v MTB để chng minh MA.MB=MT2
V d 2 T kin thc phương tích MA.MB= r2−MO2. (M nằm trong đưng tròn) Ta
xây dng bi ton sau
Bài 2: Cho điểm M nằm ở pha bên trong ca đưng tròn (O). V đưng
thẳng AB vuông gc với MO.
Chng minh MA.MB=MA2= r2−MO2.
Sử dng định lý Pitago
để chng minh MA.MB=MA2= r2−MO2. (với MA = MB)
V d 3 T kin thc về phương tch: mi điểm P nằm trên
đưng thẳng IJ Ta c phương tch đn hai đưng
tròn (O1) và (O2) l bằng nhau.
T đ ta xây dng bi ton sau
r
A
O
M
B
T
r
M
O
A
B
Thực hiện: Đặng Minh Khâm – THCS Chu Văn An Trang 5
O
2
O
1
H
G
F
E
J
I
M
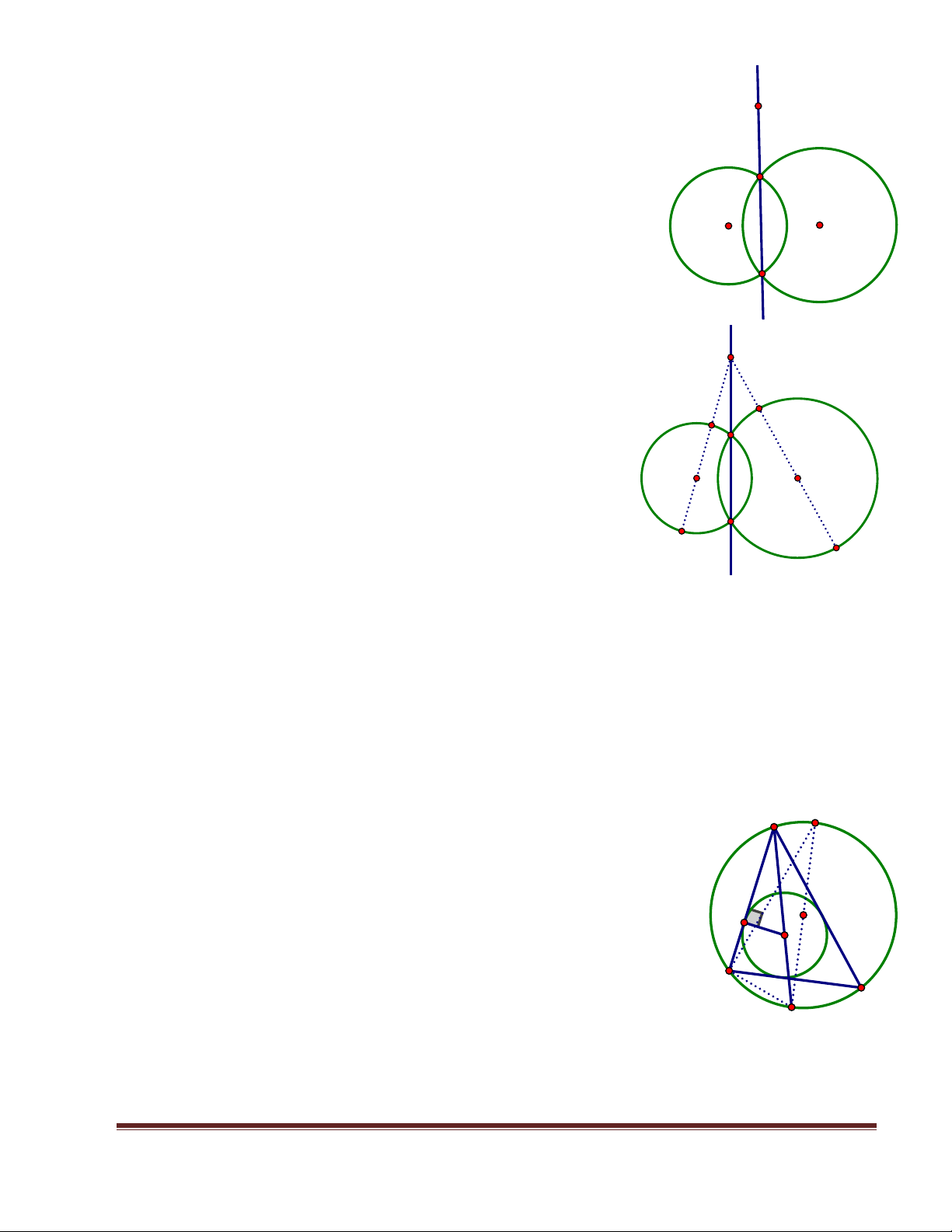
Bài 3 Cho hai đưng tròn (O1, r1) và (O2, r2) cắt nhau tại hai
điểm I và J. Chng minh rằng mi điểm M nằm trên đưng
thẳng IJ ta luôn có
2 2 2 2
1 1 2 2
MO r MO r
HDn Hc sinh v MO1 và MO2 cắt mỗi đưng tròn ln
lưt tại E, F v G, H V sử dng cc cp tam gic đồng
dạng MEI v MJF ; MIG v MHJ để
Chng minh ME.MF=MI.MJ=MG.MH
Kt hp
Chng minh ME.MF =
22
11
MO r
và MG.MH =
22
22
MO r
Bi 4: Cho đưng tròn(O; R) v (I; r) l cc cc đưng
tròn ngoại tip v ni tip tam gic ABC.
Chng minh OI2 = R2 -2Rr (Đẳng thức Euler)
HD
Gi D l giao điểm ca phân gic AI với (O)
Trong (O) chng minh đưc
IA.ID = R2- OI2 hay OI2 = R2- IA.ID
(xem phần chứng minh phương tích của một điểm nằm trong đường tròn kết hợp vẽ
thêm một đường kính qua I ) (1)
V đưng knh DE ( tạo ra tam gic vuông c cạnh l 2R)
V IH vuông gc với AB
Khi đ
chng minh đưc tam gic BDI cân tại D suy ra DB = DI (2)
chng minh đưc tam gic AIH v EDB đồng dạng
Suy ra IA.DB = ED.IH = 2R.r hay IA.ID = 2R.r (3)
T (1) (2) (3) suy ra OI2 = R2- 2Rr
(Tham kho phn lý thuyt về phương tch trong phn ph lc)
E
D
H
I
O
B
C
A
O
2
O
1
I
J
M
















