Hồi quy tuyến tính là gì?
Mô hình Hồi quy tuyến tính (Linear Regression) là một công cụ cơ bản trong
phân tích dữ liệu và học máy để mô tả mối quan hệ tuyến tính giữa một biến
phụ thuộc (y) và một biến độc lập (x)
hình 1
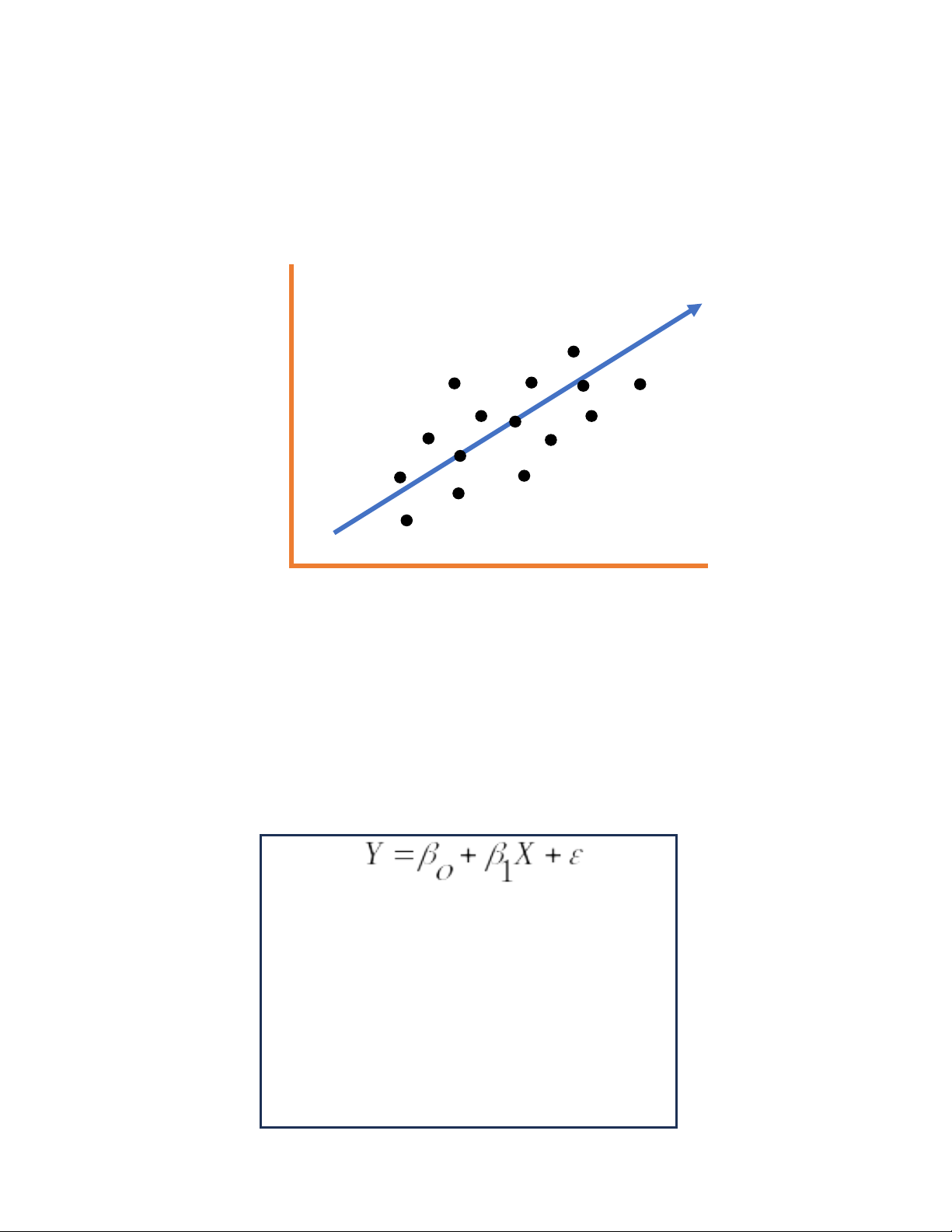
(hình 1) Mối quan hệ tuyến tính giữa các biến đầu ra (y) và biến dự báo (x) .
Đường màu xanh được gọi là đường thẳng phù hợp nhất. Dựa trên các điểm
dữ liệu đã cho, ta cố gắng vẽ một đường thẳng phù hợp nhất với các điểm.
Có 2 loại hồi quy tuyến tính:
Hồi quy tuyến tính đơn biến:
Y: biến phụ thuộc
X: biến độc lập
β0 : hệ số chặn
β1: hệ số quy chiếu
ε: sai số
Biến phụ thuộc
Biến không phụ thuộc
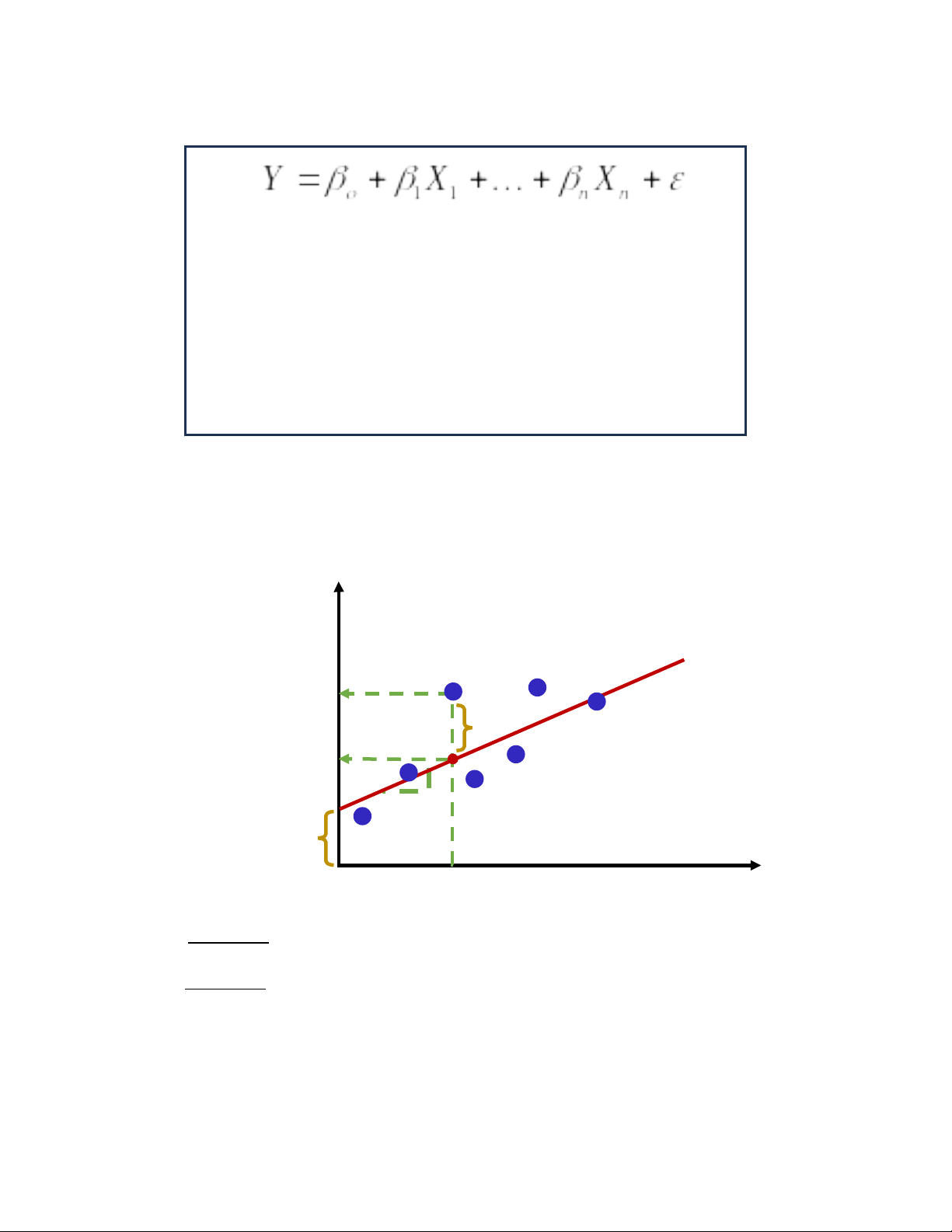
Hồi quy tuyến tính đa biến:
Y: biến phụ thuộc
X: biến độc lập
β0: hệ số chặn
β1…βn: hệ số quy chiếu riêng
ε: sai số
Mục tiêu của thuật toán hồi quy tuyến tính:
Là tìm raIcác giá trị tốt nhất cho β0 và β1 để tìm ra đường phù hợp nhất.
Đường phù hợp nhất là đường có sai số giữa các giá trị dự đoán và giá
trị thực tế phải là nhỏ nhất
β0 =
hằng số
hệ số chặn
: là giá trị trung bình của các phản hồi tạiIxI= 0
β1 =
hệ số góc
hệ số chặn
ε = ydự đoán - yi ( ydự đoán = β0 + β1X1 )
Giá trị dự đoán
của Xi
Giá trị quan sát được
của Xi
Y
X
Xi
β0
β1
εi
y = β0 + β1x
yi = β0 + β1xi + εi
Hàm mất mát (Cost Function):
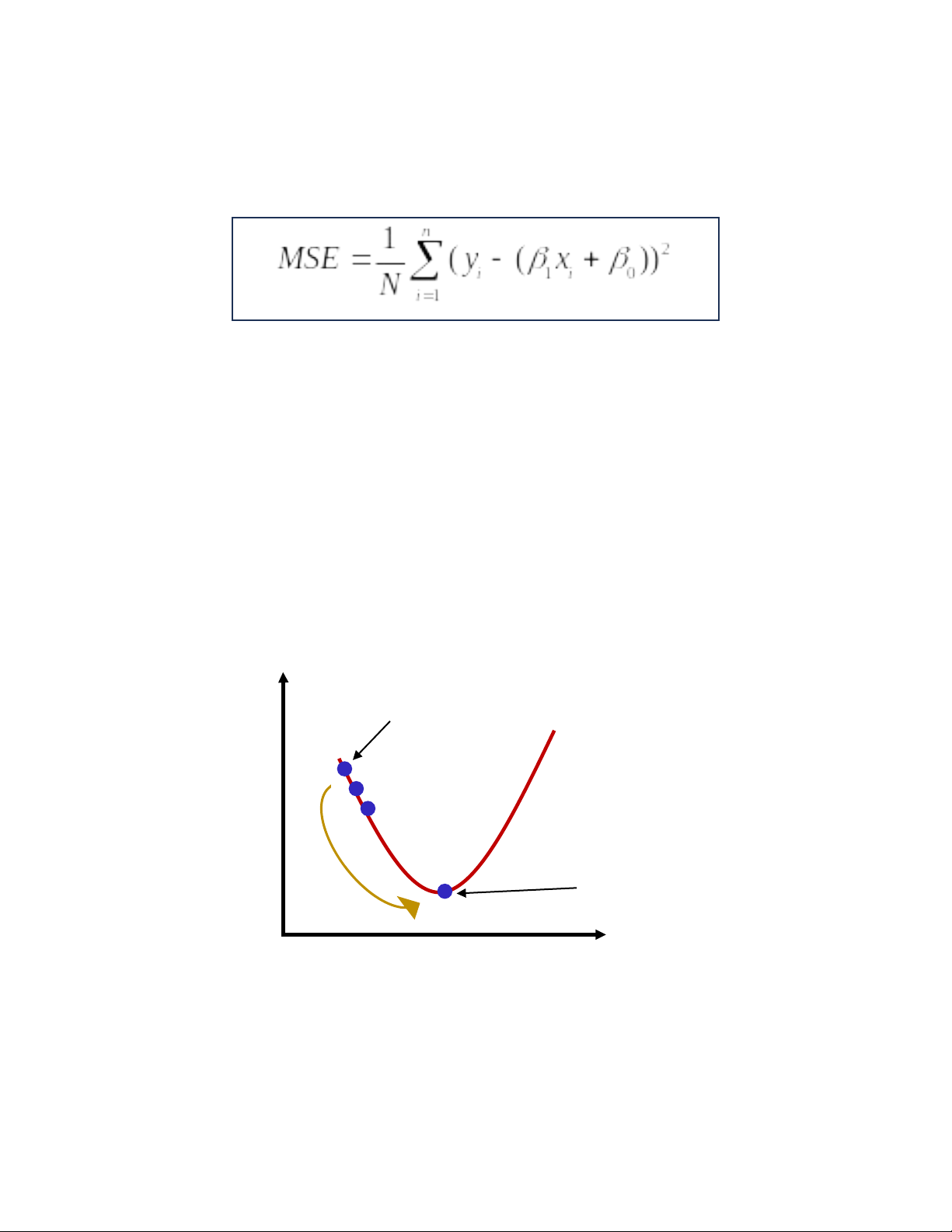
Sai số bình phương trung bình (MSE): là sai số bình phương trung bình
xảy ra giữa giá trịIIydự đoánIvàIIyi
Dụng hàm MSE để cập nhật các giá trị của β0 và β1 sao cho giá trị MSE
ổn định ở mức cực tiểu. Các tham số này có thể được xác định bằng
phương pháp giảm dần hệ số góc sao cho giá trị của hàm mất mát là cực
tiểu
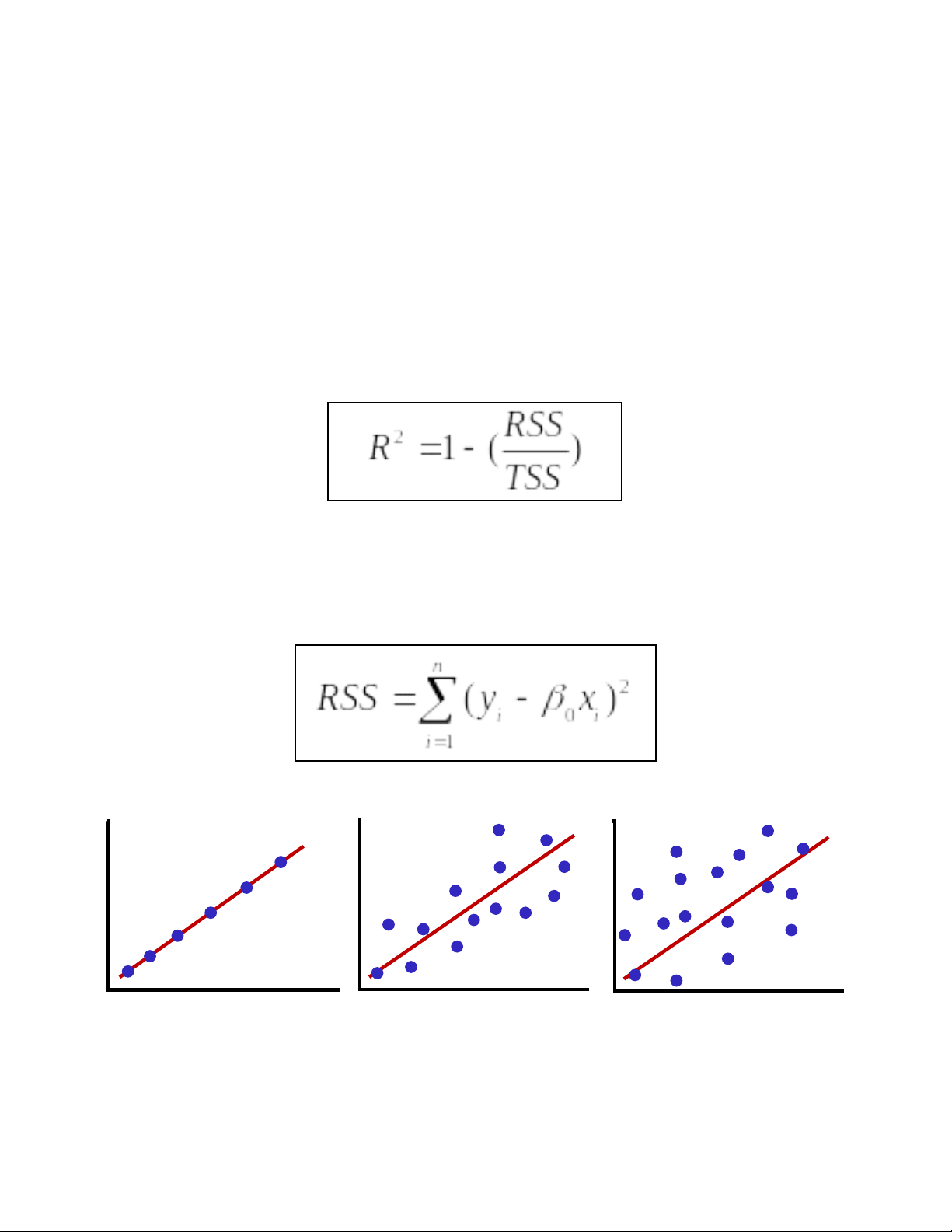
Suy giảm độ dóc (Gradient Descent):
Là một trong những thuật toán tối ưu hóa hàm mất mát để đạt được giải
pháp tối ưu. Để tìm giải pháp tối ưu, chúng ta cần giảm MSE. Điều này
được thực hiện bằng cách thay đổi các giá trị của β1 và β0 cho đến khi có
được giải pháp tối ưu cho hàm tuyến tính.
Các số liệu đánh giá cho hồi quy tuyến tính:
Giá trị ban đầu
Giá trị tối ưu
Hàm mất mát (cost function)
β0
Các số liệu đánh giá này thường cung cấp thước đo về mức độ đầu ra
quan sát được tạo ra bởi mô hình:
oHệ số xác định (R2)
oSai số bình phương trung bình (RSME)
oSai số chuẩn dư (RSE)
Hệ số xác định (R2)
Là một con số giải thích lượng biến thiên được mô hình biểu diễn từ
[0:1]. Giá trị R2 càng cao thì mô hình càng phù hợp với dữ liệu.
RSS: tổng bình phương dư
oLà tổng bình phương của phần dư cho mỗi điểm trong biểu đồ.
Đây là thước đo sự khác biệt giữa đầu ra tối ưu và đầu ra thực tế
quan sát được.
Ý nghĩa của R2:
TSS: tổng bình phương
R2 - 1 R2 - 0,005
R2 - 0,5
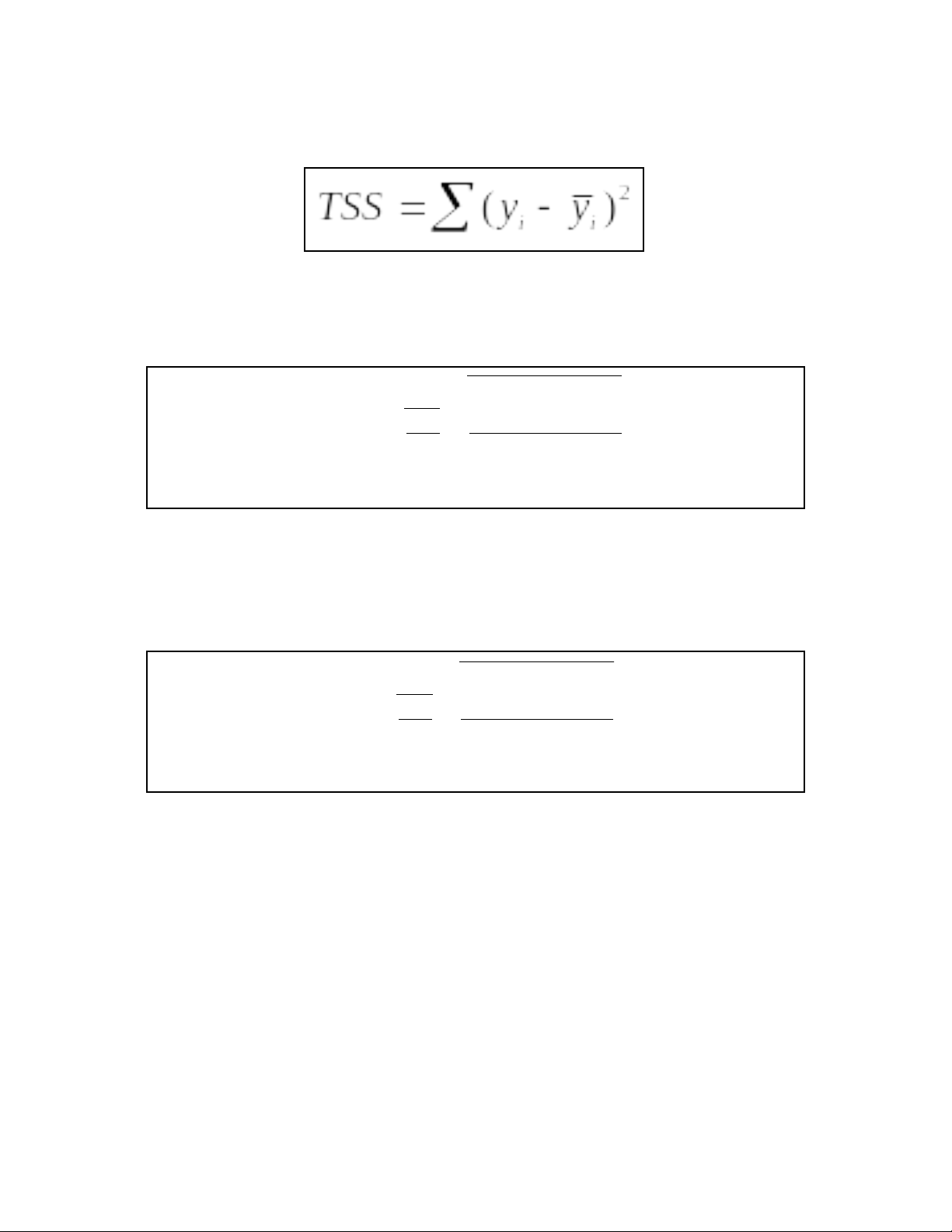
oLà tổng các sai số của các điểm từ giá trị trung bình của biến phản
hồi.
Sai số bình phương trung bình căn (RSME)
Chỉ định mức độ gần của các điểm dữ liệu quan sát được với các giá trị
dự đoán.
RMSE=
√
RSS
n=
√
∑
i=1
n
(yi
thựctế −yi
dự đoán)2
n
Sai số chuẩn dư (RSE)
Để ước tính này chính xác, người ta phải chia tổng bình phương của các
phần dư choIbậc tự doIthay vì tổng số điểm trong mô hình.
RSE=
√
RSS
df =
√
∑
i=1
n
(yi
thựctế −yi
dự đoán)2
n−2
R2 tốt hơn RSME. Vì giá trị của RSME phụ thuộc vào đơn vị của các biến
(tức là nó không phải là một phép đo chuẩn), nó có thể thay đổi theo sự
thay đổi đơn vị của các biến.
Hồi quy tuyến tính hoạt động như thế nào?
Về bản chất, một kỹ thuật hồi quy tuyến tính đơn giản cố gắng vẽ một đồ thị
đường giữa hai biến dữ liệu, x và y. Là biến độc lập, x được vẽ dọc theo trục