Chương III: NGUYÊN HÀM – TÍCH PHÂN & ỨNG DỤNG GV Nguyễn Thị Minh Dương 2020
1
TRƯỜNG THPT LƯU HOÀNG
TỔ TOÁN – TIN
***
TÀI LIỆU ÔN TẬP
TỪ NGÀY 17/2/2020 ĐẾN 29/2/2020
MÔN TOÁN LỚP 12A2 – 12A5
PHẦN A. LÝ THUYẾT
I. QUY TẮC TÍNH ĐẠO HÀM :
Hàm số
,u u x v v x
có đạo hàm tại x
'''
u v u v
'''
..u v u v uv
''
ku ku
'''
2
u u v uv
vv



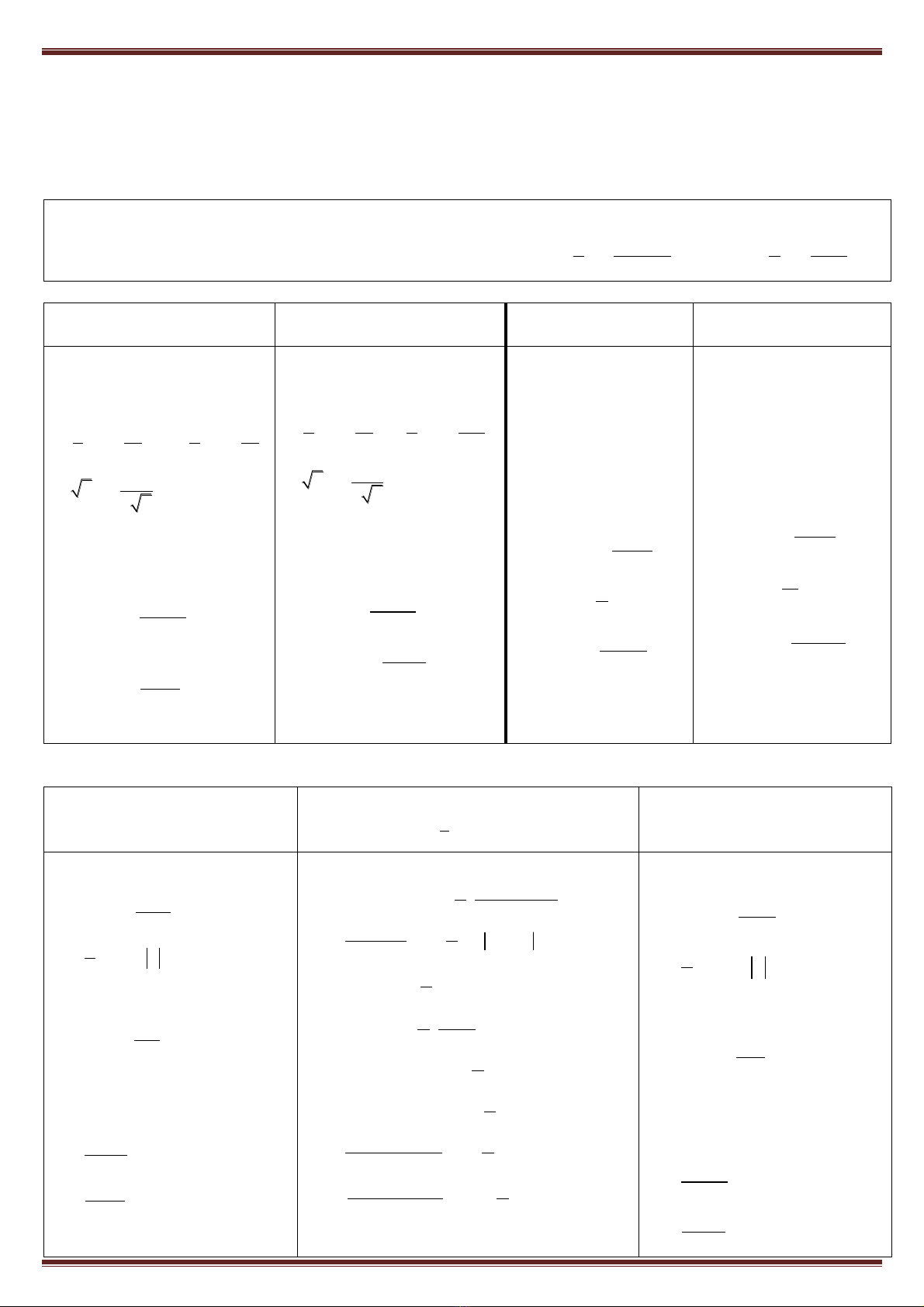
II. BẢNG CÔNG THỨC ĐẠO HÀM
Đạo hàm hàm số cơ bản
Đ.hàm h.số hợp u = u(x)
Đạo hàm h.số cơ bản
ĐH hàm số hợp u =
u(x)
'0c
'1x
'1
.xx

'
2
11
xx




'
2
kk
xx




'1
2
xx
Hm s lưng gic
'
(sin x) osxc
'
( osx) sinxc
'
2
1
(t anx) cos x
2
1 tan x
'
2
1
(cot x) sin x

2
1 cot x
'1'
..u u u

''
2
1u
uu




''
2
.k k u
uu




'
'
2
u
uu
Hm s lưng gic
''
(sin ) . osuu u c
''
( osu) .sinucu
'
'
2
(t anu) cos
u
u
'
'
2
(cot u) sin
u
u

Hm s m
'.ln
xx
a a a
'
xx
ee
'
xx
ee

Hm s Lôgarit
'1
log ln
axxa
'1
ln x x
'1
log x ln10x
''. .ln
uu
a u a a
''uu
e u e
'
'
log ln
a
u
uua
'
'
log .ln10
u
uu
------------------------------------------------o0o-----------------------------------------------
CÔNG THỨC NGUYÊN HÀM
Nguyên hàm hàm số cơ bản
Công thc b
sung
1
f(ax b)dx F(ax b) C
a
Nguyên hàm hàm số hợp u =
u(x)
1
2
2
1/
2 / 1
1
1
3 / ln
4/
5 / 0 1
ln
6 / cos sin
7 / sin cos
1
8 / tan
cos
1
9 / cot
sin
xx
x
x
dx x C
x
x dx C
dx x C
x
e dx e C
a
a dx C a
a
xdx x C
xdx x C
dx x C
x
dx x C
x





1
'
'
'
'
'
'
'
2
/////////////////////////////
1
2 / . 1
11
3 / .ln
1
4 / .
1
5 / . ln
1
6 / cos sin
1
7 / sin cos
11
8 / tan
cos



ax b ax b
kx b
kx b
ax b
ax b dx C
a
dx ax b C
ax b a
e dx e C
a
a
a dx C
ka
ax b dx ax b C
a
ax b dx ax b C
a
dx ax
ax b a
/
2
11
9 / cot
sin

bC
dx ax b C
ax b a
1
2
2
1/
2 / 1
1
1
3/ ln
4/
5 / 0 1
ln
6 / cos sin
7 / sin cos
1
8 / tan
cos
1
9 / cot
sin
uu
u
u
du u C
u
u du C
du u C
u
e du e C
a
a du C a
a
udu u C
udu u C
du u C
u
du u C
u





Chương III: NGUYÊN HÀM – TÍCH PHÂN & ỨNG DỤNG GV Nguyễn Thị Minh Dương 2020
2
*

m
nmn
x dx x dx x dx
*
1dx x dx ...
x



1
10 / tan ln cos
11/ cot ln sin

xdx x C
xdx x C
2. Tích phân
a/. Tính chất:
Giả sử các hàm số
,fg
liên tục trên
K
và
,,abc
là ba số bất kì thuộc
K
. Khi đó ta có:
1.
0
a
a
f x dx
2.
ba
ab
f x dx f x dx

3.
b c c
a b a
f x dx f x dx f x dx
4.
b b b
a a a
f x g x dx f x dx g x dx


5.
bb
aa
kf x dx k f x dx

( với
.k
)
b/ Phương pháp đổi biến số:
'
b u b
a u a
f u x u x dx f u du


Trong đó:
u u x
có đạo hàm liên tục trên
K
, hàm số
y f u
liên tục và sao cho hàm hợp
f u x


xác định trên
K
;
a
và
b
là hai số thuộc
K
.
c/ Phương pháp tích phân từng phần:
' | '
bb
b
a
aa
u x v x dx u x v x v x u x dx

Hay
|
bb
b
a
aa
udv uv vdu

Trong đó các hàm số
,uv
có đạo hàm liên tục trên
K
và
,ab
là hai số thuộc
K
PHẦN B. BÀI TẬP
Câu 1: Nguyên hàm của hàm số
3
29f x x
.
A.
4
19
2x x C
B.
C.
4
1
4xC
D.
3
49x x C
Câu 2: Nguyên hàm của hàm số
2
2
5 3 1
3
f x x xx
.
A.
331
5ln
33
xx x C
x
B.
331
5ln
33
xx x C
x
C.
331
2 5ln 3
x x x C
x
D.
24
53
2x
xC
xx
Câu 3: Nguyên hàm của hàm số
2
2
11
3
f x x
x
l.
A.
42
3
3
xx C
x


B.
31
33
xx
C
x
C.
42
3
3
xx C
x
D.
Câu 4: Nguyên hàm của hàm số
3
f x x
.
A.
32
3
4
x
F x C
B.
3
3
4
xx
F x C
C.
3
4
3
x
F x C
x

D.
32
4
3
x
F x C
x

Câu 5: Nguyên hàm của hàm số
1
fx xx
.
A.
2
F x C
x

B.
2
F x C
x
C.
2
x
F x C
D.
2
x
F x C
Câu 6: Nguyên hàm của hàm số
2
x x x
fx x
.
A.
21x
F x C
x

B.
2
21x
F x C
x

C.
23x
F x C
x

D.
12x
F x C
x

Câu 7:
3
5x dx
x



bằng:
Chương III: NGUYÊN HÀM – TÍCH PHÂN & ỨNG DỤNG GV Nguyễn Thị Minh Dương 2020
3
A.
5
2
5ln 5
x x C
B.
5
2
5ln 5
x x C
C.
5
2
5ln 5
x x C
D.
5
2
5ln 5
x x C
Câu 8:
34
xx
dx
bằng:
A.
34
ln3 ln 4
xx
C
B.
34
ln 4 ln3
xx
C
C.
43
ln3 ln 4
xx
C
D.
34
ln3 ln 4
xx
C
Câu 9:
3.2xx dx
bằng:
A.
3
22
ln 2 3
x
xC
B.
3
22
3.ln 2 3
x
xC
C.
3
22
3.ln 2 3
x
xC
D.
3
2
3.ln 2
x
xC
Câu 10: Nguyên hàm của hàm số
32
2 .3
xx
fx
là:
A.
32
23
.
3ln2 2ln3
xx
F x C
B.
72
ln72
F x C
C.
32
2 .3
ln6
xx
F x C
D.
ln72
72
F x C
Câu 11: Nguyên hàm của hàm số
3.3
xx
f x e
là:
A.
3
3
3.
ln 3.
x
e
F x C
e

B.
3
3
3.ln 3.
x
e
F x C
e

C.
3
3.
ln 3.
x
e
F x C
e

D.
3
3.
ln3
x
e
F x C
Câu 12: Nguyên hàm của hàm số
1 2 3
3 .2
xx
fx
là:
A.
8
9
8
ln 9
x
F x C




B.
9
8
38
ln 9
x
F x C




C.
8
9
38
ln 9
x
F x C




D.
8
9
39
ln 8
x
F x C




Câu 13: Nguyên hàm của hàm số
1
3
4
x
x
fx
là:
A.
4
3
33
ln 4
x
F x C




B.
3
4
3
ln 4
x
F x C




C.
2
x
F x C
D.
3
4
33
ln 4
x
F x C




Câu 14: Tính
5
31x dx
bằngA.
6
131
18 xC
B.
6
31
6
xC
C.
6
31
6
xC

D.
6
31
18
xC

Câu 15: Tính
4
2x dx
bằng A.
5
2
5
xC

B.
5
2
10
xC

C.
5
2
5
xC
D.
5
2
10
xC
Câu 16:
2
1
53
dx
x
bằngA.
1
5 5 3 C
x

B.
1
5 5 3 C
x
C.
1
53C
x

D.
1
5 5 3 C
x

Câu 17:
3
25
dx
x
bằng:A.
2ln 2 5xC
B.
3ln 2 5
2xC
C.
3ln 2 5xC
D.
3ln 2 5
2xC
Câu 18:
23
dx
x
bằng:A.
2
1
23 C
x
B.
2
3
23 C
x

C.
1ln 2 3
3xC
D.
1ln 3 2
3xC
Câu 19:
13x
e dx
bằng: A.
13
3
x
F x C
e

B.
13
3
x
e
F x C

C.
3
3
x
e
F x C
e
D.
3
3x
e
F x C
e
Câu 20:
25
1
xdx
e
là:A.
25
5
x
F x C
e

B.
25
5
x
F x C
e
C.
25
5
x
e
F x C
D.
5
2
5
x
e
F x C
e

Câu 21:
2
12 .3
3
x x x
e dx



A.
1 18
3 ln18
x
x
eC
B.
12
3 ln 2
x
x
eC
C.
13
3 ln3
x
x
eC
D.
19
3 ln9
x
x
eC
Câu 22:
1
3cos 3x
x dx
A.
3
sin ln3
x
xC
B.
3
3sin 3ln3
x
xC
C.
3
3sin ln3
x
xC
D.
3
3sin 3ln3
x
xC
Chương III: NGUYÊN HÀM – TÍCH PHÂN & ỨNG DỤNG GV Nguyễn Thị Minh Dương 2020
4
Câu 23: Nguyên hàm của hàm số
2 1 3
1sin 3 .2
3
xx
f x x

A.
1 72
cos
3 ln72
x
xC




B.
1 72
cos
3 ln72
x
xC





C.
1 72
cos
3 ln72
x
xC





D.
1 72
cos
3 ln72
x
xC




Câu 24: Nguyên hàm của hàm số
2
2
3sin os
f x x
cx

A.
3cos 2tanx x C
B.
32cos 2tan
2x x C
C.
32cos 2tan
2x x C
D.
32cos 2tan
2x x C
Câu 25: Nguyên hàm của hàm số
22
1
sin . os
fx
x c x
A.
tan tx co x C
B.
tan tx co x C
C.
11
tan cot C
xx

D.
22
11
tan cot C
xx

Câu 26: Nguyên hàm của hàm số
22
1
sin . os
fx
x c x
A.
2tan2xC
B. -2
cot2xC
C. 4
cot2xC
D. 2
cot2xC
Câu 27: Tính
2
3sin
x
xe
e dx
x




bằng
A.
3t
x
e co x C
B.
3 tan
x
e x C
C.
3t
x
e co x C
D.
2
1
3cot
x
eC
x

Câu 28: Tính
2
cos 2
3x dx



bằng
A.
12
sin 2
23
xC




B.
2
sin 2
3xC



C.
12
sin 2
23
xC



D.
2
sin 2
3xC



Câu 29: Tính
sin 3 3
x dx



bằng
A.
1sin 3
33
xC




B.
1cos 3
33
xC




C.
cos 3 3
xC



D.
1cos 3
33
xC



Câu 30: Nguyên hàm của
3
2 1 3xx
là:
A.
23
x x x C
B.
22
13x x C
C.
3
2x x x C
D.
3
26
15
x
xC





Câu 31: Tính
2
212x x dx
bằng
A.
3
312x x C
B.
3
3
112
2x x C
C.
4 1 2x x C
D.
5 4 3
12 15 5
15
x x x C

Câu 32:
2
1
33
x
xdx



bằng:
A.
2
3 ln3
ln3 3
x
xC





B.
3
1 3 1
3 ln3 3 ln3
x
xC





C.
91
2
2ln3 2.9 ln3
x
xxC
D.
11
92
2ln3 9
x
xxC



Câu 33: Tính
12
xx
e e dx
bằng A.
2
x
e x C
B.
2
2
xx
e e C
C.
2
xx
e x e C

D.
2
xx
e x e C

Câu 34: Tính
11x x x dx
bằng
A.
2
5
2x x x C
B.
2
2
5x x x C
C.
2
5x x x C
D.
5
2x x x C
Câu 35: Tính
2
x x x dx
x
bằng
Chương III: NGUYÊN HÀM – TÍCH PHÂN & ỨNG DỤNG GV Nguyễn Thị Minh Dương 2020
5
A.
21x
F x C
x

B.
2
21x
F x C
x

C.
23x
F x C
x

D.
12x
F x C
x

Câu 36: Tính
2
2
3 2 3xx
dx
x

bằng
A.
3
3 2lnx x C
x
B.
2
3
3x x x C
x

C.
2
3
33x x x
C
x

D.
2
3
33x x x
C
x

Câu 37: Tính
2
cos sinx x dx
bằng
A.
2
sin cosx x C
B.
3
sin cos
3
xx
C
C.
2 cos2
2
xx
C
D.
1cos2
2
x x C
Câu 38: Tính
2
2 sin x dx
bằng
A.
18 16cos cos2
4
x x x C

B.
3
2 cos
3
xx
C
C.
2 cos
3
xx
C
D.
3
2 cos
3
xx
C
Câu 39: Tính
44
cos sinx x dx
bằng
A.
1sin 2
2xC
B.
1sin 2
2xC
C.
55
4cos 4sinx x C
D.
55
5sin 5cosx x C
Câu40:Tính
2
cos 2xdx
bằngA.
11
sin4
24
x x C




B.
3
2sin 2
3
xC
C.
11
sin4
24
x x C




D.
11
cos4
22
x x C
Câu 41:
22
os 3
x
c dx
bằng: A.
4
32
os
23
x
cC
B.
4
12
os
23
x
cC
C.
34
sin
2 8 3
xx
C
D.
44
os
2 3 3
xx
cC
Câu 42: Tính
4
cos xdx
bằng
A.
5
1sin
5xC
B.
3
12cos
3x x C
C.
3 1 1
sin2 sin4
8 4 32
x x x C
D.
31
sin2 sin4
28
x x x C
Câu 43: Tính
2
sin 3xdx
bằng A.
11
sin6
2 12
x x C
B.
3
2cos 3
3
xC
C.
11
sin3
24
x x C




D.
11
cos6
22
x x C
Câu 48: Tính
2
cot xdx
bằng A.
cot x x C
B.
cotx xC
C.
cot x x C
D.
cot x x C
Câu 49: Tính
cos3 .cosx xdx
bằng
A.
11
sin2 sin4
48
x x C
B.
11
sin2 sin4
24
x x C
C.
11
sin2 sin4
84
x x C
D.
11
sin2 sin4
48
x x C
Câu 50: Tính
sin2 .sin3x xdx
bằng
A.
11
sin sin5
25
x x C
B.
11
sin sin5
25
x x C
C.
11
sin sin5
2 10
x x C
D.
11
sin sin5
2 10
x x C
Câu 51: Tính
sin2 .cosx xdx
bằng
A.
11
cos cos3
26
x x C
B.
11
cos cos3
26
x x C
C.
11
cos cos3
62
x x C
D.
11
cos cos3
26
x x C
Câu 52:
os4 .cos sin 4 .sinc x x x x dx
bằng:
A.
1sin5
5xC
B.
1sin3
3xC
C.
11
sin 4 os4
44
x c x C
D.
1sin 4 os4
4x c x C
Câu 53:
os8 .sinc x xdx
bằng:
A.
1sin8 . os
8x c x C
B.
1sin8 . os
8x c x C
C.
11
os7 os9
14 18
c x c x C
D.
11
os9 os7
18 14
c x c x C
Câu 54:
2
sin 2xdx
bằng: