
1
NHI T LI T CHÀO M NG CÁC TH Y Ệ Ệ Ừ Ầ
CÔ GIÁO V D Ề Ự
TP HU N GI I TOÁN TRÊN Ậ Ấ Ả
MÁY TÍNH CASIO FX570MS

2
TP HU N GI I TOÁN TRÊN MÁY Ậ Ấ Ả
TÍNH CASIO FX570MS
D NG 1:Ạ
D NG 1:Ạ TÍNH TOÁN THÔNG TH NG, LUY N K ƯỜ Ệ Ỹ
TÍNH TOÁN THÔNG TH NG, LUY N K ƯỜ Ệ Ỹ
NĂNG B M MÁYẤ
NĂNG B M MÁYẤ
D NG 2:Ạ
D NG 2:Ạ CÁC BÀI TOÁN V ĐA TH CỀ Ứ
CÁC BÀI TOÁN V ĐA TH CỀ Ứ
D NG 3:Ạ
D NG 3:Ạ PH NG TRÌNH VÀ H PH NG TRÌNHƯƠ Ệ ƯƠ
PH NG TRÌNH VÀ H PH NG TRÌNHƯƠ Ệ ƯƠ
D NG 4:Ạ
D NG 4:Ạ LÃI SU T TI T KI MẤ Ế Ệ
LÃI SU T TI T KI MẤ Ế Ệ

3
D NG 1: TÍNH TOÁN THÔNG TH NG, LUY N K Ạ ƯỜ Ệ Ỹ
D NG 1: TÍNH TOÁN THÔNG TH NG, LUY N K Ạ ƯỜ Ệ Ỹ
NĂNG B M MÁYẤ
NĂNG B M MÁYẤ
Quy trình b m phímấ
Quy trình b m phímấ bi u th cể ứ
bi u th cể ứ A
A
Quy trình b m phímấ
Quy trình b m phímấ bi u th cể ứ
bi u th cể ứ B
B
2 2
3 ^ 6 3 2 ^ 3 2 x x
+ =
( ( ) 18 55 24 ) 28 44 68
− − − − =
Vi’ d 1.ụ
Vi’ d 1.ụ
Vi t quy trình b m phím tính giá tr ế ấ ị
Vi t quy trình b m phím tính giá tr ế ấ ị
c a bi u th củ ể ứ
c a bi u th củ ể ứ
A = 3
A = 36
6:3
:32
2 + 2
+ 23
3.2
.22
2;
;
B = (- 18).(55 - 24) - 28.(44 - 68).
B = (- 18).(55 - 24) - 28.(44 - 68).
Bài gi iả
Bài gi iả
KQ:
KQ: B = 113; D = 114.
B = 113; D = 114.

4
D NG 1: TÍNH TOÁN THÔNG TH NG, LUY N Ạ ƯỜ Ệ
D NG 1: TÍNH TOÁN THÔNG TH NG, LUY N Ạ ƯỜ Ệ
K NĂNG B M MÁYỸ Ấ
K NĂNG B M MÁYỸ Ấ
Vi’ d 2.ụ
Vi’ d 2.ụ
Vi t quy trình b m phím tính giá tr ế ấ ị
Vi t quy trình b m phím tính giá tr ế ấ ị
c a bi u th củ ể ứ
c a bi u th củ ể ứ
2 2
(1986 -1992)×(1986 +3972-3)×1987
B = 1983×1985×1988×1989
1 2 3 6 2
A = 1 +2 : 1 - : 1,5+2 +3,7
3 5 4 4 5
� �� �� �
� �� �� �
� �� �� �
5
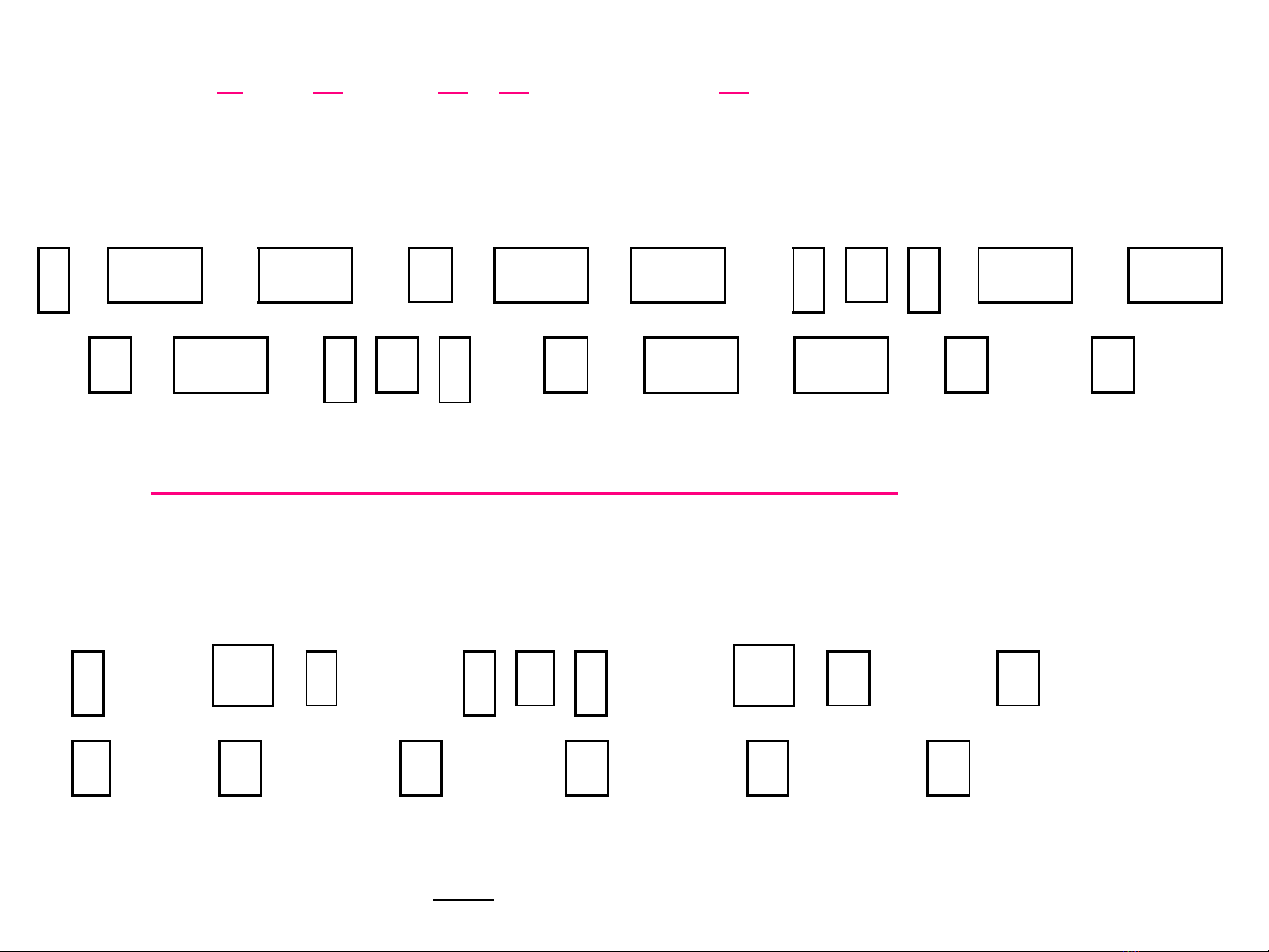
2 2
(1986 -1992)×(1986 +3972-3)×1987
B= 1983×1985×1988×1989
1 2 3 6 2
A= 1 +2 : 1 - : 1,5+2 +3,7
3 5 4 4 5
� �� �� �
� �� �� �
� �� �� �
112
A= ; B = 1987
57
KQ
Quy trình b m phímấ
Quy trình b m phímấ bi u th cể ứ
bi u th cể ứ A
A
Quy trình b m phímấ
Quy trình b m phímấ bi u th cể ứ
bi u th cể ứ B
B
( 1 ab/c 1 ab/c 3 2 ab/c 2 ab/c 5 ) ( 1 ab/c 3 ab/c
4 6 ab/c 4 ) ( 1,5 2 ab/c 2 ab/c 5 3,7
+
− + + =
2 2
( 1986 - 1992 ) ( 1986 3972 3
1987 1983 1985 1988 1989
x x
+ −
=














![Ô nhiễm môi trường không khí: Bài tiểu luận [Nổi bật/Chi tiết/Phân tích]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251011/kimphuong1001/135x160/76241760173495.jpg)







![Ứng dụng kỹ thuật trao đổi ion trong điện phân: Bài tiểu luận [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250829/sonphamxuan1808/135x160/97341756442892.jpg)



