- 1 -
M Đ UỞ Ầ
Nh ng k thu t đi u khi n truy n th ng nh đi u khi n Tích phân tữ ỹ ậ ề ể ề ố ư ề ể ỉ
l (PI) hay đi u khi n Vi tích phân t l (PID) đ c ng d ng thành công trongệ ề ể ỉ ệ ượ ứ ụ
đi u khi n nh ng quá trình tuy n tính. G n đây, đi u khi n tiên đoán môề ể ữ ế ầ ề ể
hình (MPC) cũng th c hi n thành công trong đi u khi n nh ng h th ngự ệ ề ể ữ ệ ố
tuy n tính. Tuy nhiên, kho ng 90% nh ng quá trình sinh h c và hoá h c là phiế ả ữ ọ ọ
tuy n cao và h u h t chúng là nh ng h MIMO.Khi h th ng là phi tuy nế ầ ế ữ ệ ệ ố ế
và/ho c MIMO, nh ng k thu t truy n th ng trên th ng m c ph i sai sótặ ữ ỹ ậ ề ố ườ ắ ả
khi đi u khi n nh ng h th ng nh th . Ngày nay, nh ng h th ng đ cề ể ữ ệ ố ư ế ữ ệ ố ượ
dùng trong công nghi p đòi h i đ t qu n cao và nh ng k thu t trên khôngệ ỏ ộ ự ả ữ ỹ ậ
có kh năng đ đ t đ c đi u này.ả ể ạ ượ ề
C n ph i đ t đ c nh ng đòi h i đi u khi n tăng nhanh trong nh ng hầ ả ạ ượ ữ ỏ ề ể ữ ệ
th ng đi u khi n đ ng ph c t p d i nh ng thay đ i quan tr ng đã làm choố ề ể ộ ứ ạ ướ ữ ổ ọ
vi c dùng nh ng k thu t thông minh nh m ng n ron, lôgic m và thu tệ ữ ỹ ậ ư ạ ơ ờ ậ
gi i di truy n trong nh ng h th ng đi u khi n tr nên h p d n. Nh ng lýả ề ữ ệ ố ề ể ở ấ ẫ ữ
do chính đ ng sau đi u này là kh năng c a chúng có th “h c” đ x p xằ ề ả ủ ể ọ ể ấ ỉ
hàm và phân lo i m u và ti m năng c a chúng trong th c thi ph n c ng songạ ẫ ề ủ ự ầ ứ
song đ s , ồ ộ ph ng pháp đi u khi n thông minh ph ng theo quá trình x lýươ ề ể ỏ ử
thông tin không rõ ràng và ra quy t đ nh đi u khi n c a con ng i cũng nhế ị ề ể ủ ườ ư
b t ch c quá trình ti n hoá sinh h c đ t o ra gi i pháp t i u. Nói cáchắ ướ ế ọ ể ạ ả ố ư
khác, chúng có kh năng th c thi (c ph n m m và ph n c ng) nhi u ch cả ự ả ầ ề ầ ứ ề ứ
năng c n thi t đ đi u khi n h th ng v i đ t qu n cao.ầ ế ể ề ể ệ ố ớ ộ ự ả
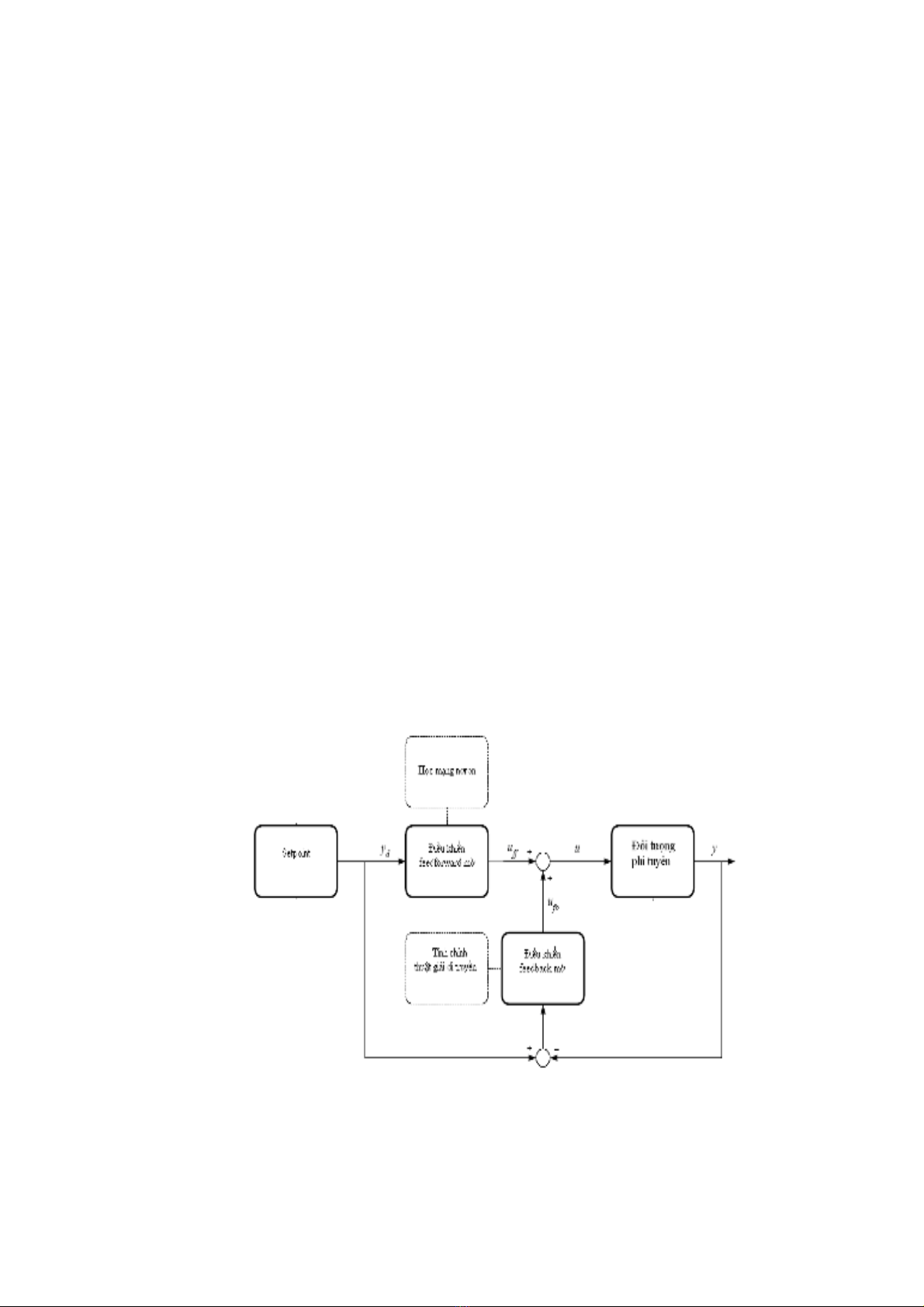
S đ h th ng đi u khi n đ c mô t nh sau:ơ ồ ệ ố ề ể ượ ả ư
Hình i. S đ đi u khi n đ i t ng phi tuy nơ ồ ề ể ố ượ ế
Nh v y, đây có hai b đi u khi n:ư ậ ở ộ ề ể
- 2 -
•Đi u khi n Feedforward : là b đi u khi n neuro-m cung c p nh ng tínề ể ộ ề ể ờ ấ ữ
hi u đi u khi n chính đ lái đ i t ng phi tuy n theo đúng qu đ oệ ề ể ể ố ượ ế ỹ ạ
setpoint. B đi u khi n này là b đi u khi n m ng d ng kh năng h cộ ề ể ộ ề ể ờ ứ ụ ả ọ
c a m ng n ron đ tinh ch nh nh ng thông s c a nó.ủ ạ ơ ể ỉ ữ ố ủ
•Đi u khi n Feedback: bù tín hi u, nó cung c p nh ng tín hi u đi uề ể ệ ấ ữ ệ ề
khi n hi u ch nh c n thi t đ đi u ch nh và lo i nhi u trong nh ng lânể ệ ỉ ầ ế ể ề ỉ ạ ễ ữ
c n nh xung quanh qu đ o đi u khi n. B đi u khi n này cũng là bậ ỏ ỹ ạ ề ể ộ ề ể ộ
đi u khi n m nh ng ng d ng thu t gi i di truy n đ tinh ch nh thôngề ể ờ ư ứ ụ ậ ả ề ể ỉ
s c a nó.ố ủ
K t qu mô ph ng cho th y s đ đi u khi n trên đã lái đ i t ng phi tuy nế ả ỏ ấ ơ ồ ề ể ố ượ ế
đi xuyên su t kho ng công tác c a nó v i đ chính xác cao.ố ả ủ ớ ộ
Ph n sau đây s đ c p đ n đ i t ng phi tuy n và nh ng k thu t đi uầ ẽ ề ậ ế ố ượ ế ữ ỹ ậ ề
khi n đ c thi t l p trong lu n văn.ể ượ ế ậ ậ
Trong b i c nh hi n th i, vi c s n xu t năng l ng đ i m t v i r t nhi uố ả ệ ờ ệ ả ấ ượ ố ặ ớ ấ ề
v n đ khó khăn. Trong s đó, đi u quan tr ng nh t là: tu i th c a thi t bấ ề ố ề ọ ấ ổ ọ ủ ế ị
chính t i nh ng t h p năng l ng, đ u t tài chính không ch c ch n choạ ữ ổ ợ ượ ầ ư ắ ắ
nh ng t h p m i, vi c c nh tranh gi a nh ng nhà s n xu t năng l ng đ cữ ổ ợ ớ ệ ạ ữ ữ ả ấ ượ ộ
l p đ tho mãn đòi h i năng l ng c a ng i dùng và nh ng áp l c đ đ tậ ể ả ỏ ượ ủ ườ ữ ự ể ạ
đ c nh ng yêu c u qu n lý nghiêm ng t đ s d ng t i đa ngu n tàiượ ữ ầ ả ặ ể ử ụ ố ồ
nguyên thiên nhiên và t i thi u nh h ng đ n môi tr ng.ố ể ả ưở ế ườ
Vi c v n hành c a t h p năng l ng nhiên li u than (NLNLT), lo i tệ ậ ủ ổ ợ ượ ệ ạ ổ
h p đ c dùng r ng rãi nh t cho vi c s n xu t năng l ng, đã b tác đ ngợ ượ ộ ấ ệ ả ấ ượ ị ộ
m nh. Đ u tiên, m t NLNLT ph i h tr m c tiêu chính c a h th ng năngạ ầ ộ ả ổ ợ ụ ủ ệ ố
l ng là đáp ng yêu c u t i cho năng l ng đi n m i th i đi m, đi nượ ứ ầ ả ượ ệ ở ọ ờ ể ở ệ
áp không đ i và t n s không đ i. Sau đó là vi c c nh tranh gi a tính thi tổ ầ ố ổ ệ ạ ữ ế
th c và yêu c u th tr ng khác đã tăng c ng vi c dùng NLNLT [Armorự ầ ị ườ ườ ệ
1985]. Cu i cùng, nh ng yêu c u nghiêm ng t trong vi c b o trì và kéo dàiố ữ ầ ặ ệ ả
tu i th c a thi t b chính và nh ng lu t gi m nh h ng đ n môi tr ngổ ọ ủ ế ị ữ ậ ả ả ưở ế ườ
c n ph i đ c tuân th . Trong đó:ầ ả ượ ủ
•Nh ng yêu c u v n hành chu kỳ c a NLNLT trong kho ng t i r ngữ ầ ậ ủ ả ả ộ
m c dù chúng đ c thi t k cho v n hành t i không đ i. Nh ng yêuặ ượ ế ế ậ ở ả ổ ữ
c u bi n đ i t i có th đ n t nh ng chi n l c kinh t đ c tínhầ ế ổ ả ể ế ừ ữ ế ượ ế ượ
toán t i nh ng trung tâm năng l ng hay t nh ng dao đ ng t i hạ ữ ượ ừ ữ ộ ả ệ
th ng. V n hành theo t i tin c y và hi u qu s đ m b o vi c thoố ậ ả ậ ệ ả ẽ ả ả ệ ả
mãn hàng ngày, hàng tu n và theo mùa c a yêu c u năng l ng đi n vàầ ủ ầ ượ ệ
nh ng thay đ i t i ng u nhiên không đoán tr c cho đ n nh ng gi iữ ổ ả ẫ ướ ế ữ ớ
h n v t lý c a t h p.ạ ậ ủ ổ ợ
•Vi c kéo dài tu i th thi t b là quan tr ng vì nó t i đa vi c dùng tàiệ ổ ọ ế ị ọ ố ệ
s n, gi i h n th i gian ch t và t i thi u nh ng chi phí v n hành và b oả ớ ạ ờ ế ố ể ữ ậ ả
trì. Nguyên nhân chính c a vòng đ i ng n c a b t kỳ h th ng nào làủ ờ ắ ủ ấ ệ ố
v n hành ng su t cao. Trong NLNLT, nh ng ng su t nhi t phậ ứ ấ ữ ứ ấ ệ ụ
thu c vào nh ng dao đ ng áp su t và nhi t đ h i là đ c bi t quanộ ữ ộ ấ ệ ộ ơ ặ ệ
- 3 -
tr ng. H u h t ng su t nghiêm tr ng x y ra trong su t quá trình kh iọ ầ ế ứ ấ ọ ả ố ở
đ ng và nh ng bi n đ i t i l n đ t ng t.ộ ữ ế ổ ả ớ ộ ộ
•M t NLNLT có hi u su t trong kho ng 30 đ n 35%, nghĩa là t c độ ệ ấ ả ế ố ộ
nhi t trong kho ng 11400-9800 Btu/KWh. T c đ nhi t ch u nhệ ả ố ộ ệ ị ả
h ng b i nhi u h s , ch ng h n nh ng đi u ki n h i, áp su t bưở ở ề ệ ố ẳ ạ ữ ề ệ ơ ấ ộ
ng ng t , nhi t đ n c làm mát, nhi t đ môi tr ng, khí áp,…T cư ụ ệ ộ ướ ệ ộ ườ ố
đ nhi t tăng khi làm vi c t i nh ng t i khác v i t i c s . Vi c tiêuộ ệ ệ ạ ữ ả ớ ả ơ ở ệ
t n nhiên li u và giá c làm cho vi c c i ti n t c đ nhi t nh là m tố ệ ả ệ ả ế ố ộ ệ ư ộ
tiêu chu n v m c kinh t .ẩ ề ặ ế
•Vi c tr n không hoàn h o gi a không khí và nhiên li u s làm v tệ ộ ả ữ ệ ẽ ượ
quá l ng không khí đ tránh vi c nhiên li u không đ c đ t h t, màượ ể ệ ệ ượ ố ế
s d n đ n vi c t o khói đen và khí CO đ c cũng nh nh ng l ngẽ ẫ ế ệ ạ ộ ư ữ ượ
nhiên li u d khá nguy hi m. Bên c nh đó l ng không khí d s dệ ư ể ạ ượ ư ẽ ễ
hình thành nh ng ch t không mong mu n khác nh sunfua dioxit,ữ ấ ố ư
nitrogen oxit và làm giãm hi u su t boiler do nhi t b tiêu phí trong khíệ ấ ệ ị
nhiên li u.ệ
T c nh ng yêu c u đ c đ c p trên đã d n đ n vi c phát tri nấ ả ữ ầ ượ ề ậ ở ẫ ế ệ ể
nh ng ph ng pháp đi u khi n linh ho t và toàn di n h n. Chúng cũng cungữ ươ ề ể ạ ệ ơ
c p nh ng ch c năng c n thi t cho vi c v n hành theo t i di n r ng ch tấ ữ ứ ầ ế ệ ậ ả ệ ộ ấ
l ng cao và đ ng th i cũng tho mãn nh ng ràng bu c trong vi c b o qu nượ ồ ờ ả ữ ộ ệ ả ả
và kéo dài tu i th c a thi t b chính, gi i phóng ch t ô nhi m và tiêu t nổ ọ ủ ế ị ả ấ ễ ố
nhiên li u d i nh ng thay đ i v t lý và nh ng đi u ki n kinh t . Do đó,ệ ướ ữ ổ ậ ữ ề ệ ế
ngay c khi theo t i cũng c n xem xét vi c n đ nh t n s và đi n áp, nh ngả ả ầ ệ ổ ị ầ ố ệ ữ
h th ng đi u khi n hi u qu h n cũng c n đ c thi t k đ tho mãn t iệ ố ề ể ệ ả ơ ầ ượ ế ế ể ả ố
u nh ng m c tiêu v n hành, nh ng xung đ t t ng quát đ mà NLNLT cóư ữ ụ ậ ữ ộ ổ ể
th v n hành thành công d i b t kỳ tình hu ng ho t đ ng nào.ể ậ ướ ấ ố ạ ộ
Bên c nh đó, d i nh ng đòi h i c a th tr ng hi n th i, m t ph ngạ ướ ữ ỏ ủ ị ườ ệ ờ ộ ươ
pháp toàn b cho v n hành và đi u khi n nh ng t h p năng l ng là r tộ ậ ề ể ữ ổ ợ ượ ấ
quan tr ng cho s t n t i c a b t kỳ h th ng đi n nào. Khi đ c ng d ngọ ự ồ ạ ủ ấ ệ ố ệ ượ ứ ụ
hoàn h o, nh ng h th ng đi u khi n và nh ng thi t b có th tăng c ngả ữ ệ ố ề ể ữ ế ị ể ườ
hi u su t v n hành máy, tính n đ nh và tin c y cũng nh s s n sàng, vì thệ ấ ậ ổ ị ậ ư ự ẵ ế
làm gi m vi c tiêu t n nhiên li u, chi phí v n hành và b o trì mà h u nh r tả ệ ố ệ ậ ả ầ ư ấ
t n kém trong m t t h p năng l ng. Vì v y, th t c n thi t đ phát tri nố ộ ổ ợ ượ ậ ậ ầ ế ể ể
nh ng h th ng t đ ng hi u qu và liên quan m t thi t đ n toàn b chi nữ ệ ố ự ộ ệ ả ậ ế ế ộ ế
l c và h th ng đi u khi n c a t h p đ gi chúng v n hành hi u qu vàượ ệ ố ề ể ủ ổ ợ ể ữ ậ ệ ả
có l i.ợ
Cũng c n l u ý r ng vi c s d ng r t nhi u h th ng đi u khi n và thi tầ ư ằ ệ ử ụ ấ ề ệ ố ề ể ế
b d a trên máy tính v i nh ng d ng c k thu t s x lý thông tin m nh mị ự ớ ữ ụ ụ ỹ ậ ố ử ạ ẽ
và tin c y h n cho phép nh ng nhà thi t k t p trung nhi u h n trên vi cậ ơ ữ ế ế ậ ề ơ ệ
th c thi nh ng ng d ng ph n m m đáp ng nh ng th thách đ c đ c p ự ữ ứ ụ ầ ề ứ ữ ử ượ ề ậ ở
ph n trên. Vì tính linh ho t c a ph n m m, và nh ng chi phí cho vi c phátầ ạ ủ ầ ề ữ ệ
tri n và b o trì có th d dàng cài đ t vào nh ng ph n c ng mà nó ch yể ả ể ễ ặ ữ ầ ứ ạ
- 4 -
trong đó, nh ng n l c l n trong vi c thi t k và phát tri n nh ng h th ngữ ổ ự ớ ệ ế ế ể ữ ệ ố
ph n m m toàn di n và t ng quát đ d dàng k t h p nh ng ng d ng v nầ ề ệ ổ ể ễ ế ợ ữ ứ ụ ậ
hành ti n l i( ví d , b o v , đi u khi n và t đ ng hoá) đ tăng c ng hi uệ ợ ụ ả ệ ề ể ự ộ ể ườ ệ
su t c a nh ng t h p năng l ng [Garduno and Sanchez 1995, Garcia andấ ủ ữ ổ ợ ượ
Garduno 1998].
Trong lu n văn này tác gi s thi t k m t h th ng đi u khi n toàn b .ậ ả ẽ ế ế ộ ệ ố ề ể ộ
H th ng này s k t h p gi a các lĩnh v c k thu t đi u khi n, k thu tệ ố ẽ ế ợ ữ ự ỹ ậ ề ể ỹ ậ
ph n m m và k thu t quá trình. Trong đó k thu t ph n m m đ c xem làầ ề ỹ ậ ỹ ậ ầ ề ượ
r t quan tr ng đ thi t k h th ng đi u khi n cho NLNLT.ấ ọ ể ế ế ệ ố ề ể
- 5 -
CH NG I.ƯƠ
T NG QUANỔ
1.1 Gi i thi u v m ng n ron và logic mớ ệ ề ạ ơ ờ
Vào cu i th p k 80 công ty Addison Wesley Publishing Company đã gâyố ậ ỷ
xôn xao d lu n khi tung ra th tr ng Neural Network (M ng trí tu th nư ậ ị ườ ạ ệ ầ
kinh) đ c ví nh là m t k x o k thu t gia công các thông tin m i, nhanhượ ư ộ ỹ ả ỹ ậ ớ
và chính xác. Chúng là các máy tính b t ch c cách s ng gi ng h th ngắ ướ ố ố ệ ố
th n kinh, các máy tính này làm vi c khá khác bi t so v i các máy tính thôngầ ệ ệ ớ
th ng. N ron Network x lý nhi u d li u song song t i cùng m t th iườ ơ ử ề ữ ệ ạ ộ ờ
đi m, không ph i là x lý t ng d li u m t. Chúng x lý r t nhi u d li uể ả ử ừ ữ ệ ộ ử ấ ề ữ ệ
đ u vào cùng m t lúc, c ng c tăng c ng m t vài cái này, thu nh gi m b tầ ộ ủ ố ườ ộ ỏ ả ớ
nh ng cái khác. Đa s chúng đ u ph i làm theo m t khuôn m u cho tr c.ữ ố ề ả ộ ẫ ướ
Chúng tìm ki m m u trong hàng lo t các thí d , nh n d ng m u, tìm ki mế ẫ ạ ụ ậ ạ ẫ ế
các m u đ y đ t ngu n d li u trong h th ng, ho c xây d ng l i m uẫ ầ ủ ừ ồ ữ ệ ệ ố ặ ự ạ ẫ
đúng t cái b bóp méo. R t nhi u các ví d ph i làm v i s am hi u sángừ ị ấ ề ụ ả ớ ự ể
s t và các d li u khách quan nh th giác, thính giác và các tín hi u khác.ưố ữ ệ ư ị ệ
Nhìn chung, các ví d ch ng t cách ch y này có nhi u đ c tính c a conụ ứ ỏ ạ ề ặ ủ
ng i h n là các máy tính đ c l p trình s n.ườ ơ ượ ậ ẵ
Ngày nay, trí tu nhân t o đang phát tri n m nh m nh m t o ra c s xâyệ ạ ể ạ ẽ ằ ạ ơ ở
d ng các h chuyên gia, h tr giúp quy t đ nh. Trí tu nhân t o đ c xâyự ệ ệ ợ ế ị ệ ạ ượ
d ng trên c s m ng n ron nhân t o và ng d ng trong thi t k h th ngự ơ ở ạ ơ ạ ứ ụ ế ế ệ ố
đi u khi n thông minh mà trong đó b đi u khi n có kh năng t duy nh bề ể ộ ề ể ả ư ư ộ
não c a con ng i đang là xu h ng m i trong đi u khi n t đ ng. M ngủ ườ ướ ớ ề ể ự ộ ạ
n ron là s tái t o b ng k thu t nh ng ch c năng c a h th n kinh conơ ự ạ ằ ỹ ậ ữ ứ ủ ệ ầ
ng i v i vô s các n ron đ c liên k t truy n thông v i nhau trong m ng.ườ ớ ố ơ ượ ế ề ớ ạ
Đi u khi n m là m t ph ng pháp đi u khi n thông minh ph ng theo quáề ể ờ ộ ươ ề ể ỏ
trình x lý thông tin không rõ ràng và ra quy t đ nh đi u khi n c a conử ế ị ề ể ủ
ng i. Ph ng pháp này r t thích h p đ đi u khi n các đ i t ng ph cườ ươ ấ ợ ể ề ể ố ượ ứ
t p, không xác đ nh đ c mô hình toán và các đ i t ng phi tuy n. Tuyạ ị ượ ố ượ ế
nhiên, b đi u khi n m th ng đ c thi t k b i quan đi m, cách nhìnộ ề ể ờ ườ ượ ế ế ở ể
riêng c a ng i thi t k . Ng i thi t k bi n s hi u bi t, kinh nghi mủ ườ ế ế ườ ế ế ế ự ể ế ệ
c a mình v quá trình c n đi u khi n thành các bi n ngôn ng và các qui t củ ề ầ ề ể ế ữ ắ
m mô t m i quan h gi a chúng. Do đó công vi c thi t k th ng mangờ ả ố ệ ữ ệ ế ế ườ