TR NG ĐI H C S PH M THÀNH PH H CHÍƯỜ Ạ Ọ Ư Ạ Ố Ồ
MINH
KHOA V T LÝẬ
Đ tàiề
H T A Đ C CỆ Ọ Ộ Ự
Gi ng viên:ả Nguy n Vũ Th Nhânễ ụ
Nhóm th c hi n: ự ệ Nguy n Bình Anễ
Tr n Th Vĩnh Đàoầ ị
Tr n Gia Linhầ
1
Tp. HCM, 2016
L I NGỜ Ỏ
T a đ c a m t c a đi m là m t b s đc tr ng cho v trí c a đi m đó trongọ ộ ủ ộ ủ ể ộ ộ ố ặ ư ị ủ ể
m t ph ng, không gian. T a đ này luôn g n li n v i m t h t a đ xác đnhặ ẳ ọ ộ ắ ề ớ ộ ệ ọ ộ ị
bao g m g c t a đ và các tr c t a đ.ồ ố ọ ộ ụ ọ ộ
T tr c đn nay, ta th ng quen v i h t a đ Decartes t c là h t a đừ ướ ế ườ ớ ệ ọ ộ ứ ệ ọ ộ
xác đnh v trí c a m t đi m trên m t ph ng cho tr c d a vào c p s t a đị ị ủ ộ ể ặ ẳ ướ ự ặ ố ọ ộ
(x;y) hay (x;y;z).Tuy nhiên, trên th c t , trong m t s tr ng h p, ta c n sự ế ộ ố ườ ợ ầ ử
d ng đn m t s h t a đ khác, trong đó bao g m h t a đ c c. H t aụ ế ộ ố ệ ọ ộ ồ ệ ọ ộ ự ệ ọ
đ này có u đi m l n nh t khi kh o sát nh ng đng cong xu t hi n m iộ ư ể ớ ấ ả ữ ườ ấ ệ ố
quan h đc bi t v i g c t a đ.ệ ặ ệ ớ ố ọ ộ
Ngoài ra, h t a đ c c cũng là m t h t a đ đ thú v , đc bi t là trong v nệ ọ ộ ự ộ ệ ọ ộ ủ ị ặ ệ ấ
đ kh o sát hàm s đ nhi u ng i ph i say mê v i nó.ề ả ố ể ề ườ ả ớ
M c khác, nh ng tri th c mà h t a đ c c đem l i cho chúng ta khá thú vặ ữ ứ ệ ọ ộ ự ạ ị
,b ích và c n thi t. Nh ng tri th c đó có th đc v n d ng đ nghiên c u,ổ ầ ế ữ ứ ể ượ ậ ụ ể ứ
gi i đáp m t s bài t p m t cách d dàng h n so v i nhi u ph ng phápả ộ ố ậ ộ ể ơ ớ ề ươ
khác hay có th ng d ng đc trong m t s lĩnh v c thi t th c nh hàngể ứ ụ ượ ộ ố ự ế ự ư
h i, thiên văn,....ả
Chính vì nh ng lý do trên mà nhóm đã quy t đnh ch n “ Kh o sát hàm sữ ế ị ọ ả ố
trong h t a đ c c” làm đ tài ti u lu n.ệ ọ ộ ự ề ể ậ
Trong quá trình th c hi n, nhóm v n còn nhi u thi u sót. Mong nh n đc sự ệ ẫ ề ế ậ ượ ự
góp ý t th y.ừ ầ
2
H T A Đ C CỆ Ọ Ộ Ự
Ngoài t a đ Descartes th ng g p trong ch ng trình h c ph thông thì họ ộ ườ ặ ươ ọ ổ ệ
t a đ c c cũng là m t trong nh ng công c giúp ta gi i quy t m t s bàiọ ộ ự ộ ữ ụ ả ế ộ ố
toán mà h Descartes khó có th gi i quy t đc. H t a đ c c h u íchệ ể ả ế ượ ệ ọ ộ ự ữ
trong nh ng tr ng h p trong đó quan h gi a hai đi m đc vi t d i d ngữ ườ ợ ệ ữ ể ượ ế ướ ạ
góc và kho ng cách.ả
I.ĐNH NGHĨAỊ
H t a đ c c là m t h t a đ 2 chi u, trong đó m i đi m b t kì đc bi u di nệ ọ ộ ự ộ ệ ọ ộ ề ỗ ể ấ ượ ể ễ
b ng 2 thành ph n:ẳ ầ
Kho ng cách t đi m đó đn g c Oả ừ ể ế ố (g c c c) g i là bán kính.ố ự ọ
Góc t o b i đng th ng t O đn đi mạ ở ườ ẳ ừ ế ể đó v i h ng g c cho ớ ướ ố
tr c (tr c c c).ướ ụ ự
C th : Khi xét t a đ c a đi m M trên h t a đ c c nh hình ta d a vào bán kínhụ ể ọ ộ ủ ể ệ ọ ộ ự ư ự
véct ơ và góc đnh h ng gi a OM và tr c Ox t c là góc .ị ướ ữ ụ ứ
1. Bán kính và h ng: ướ
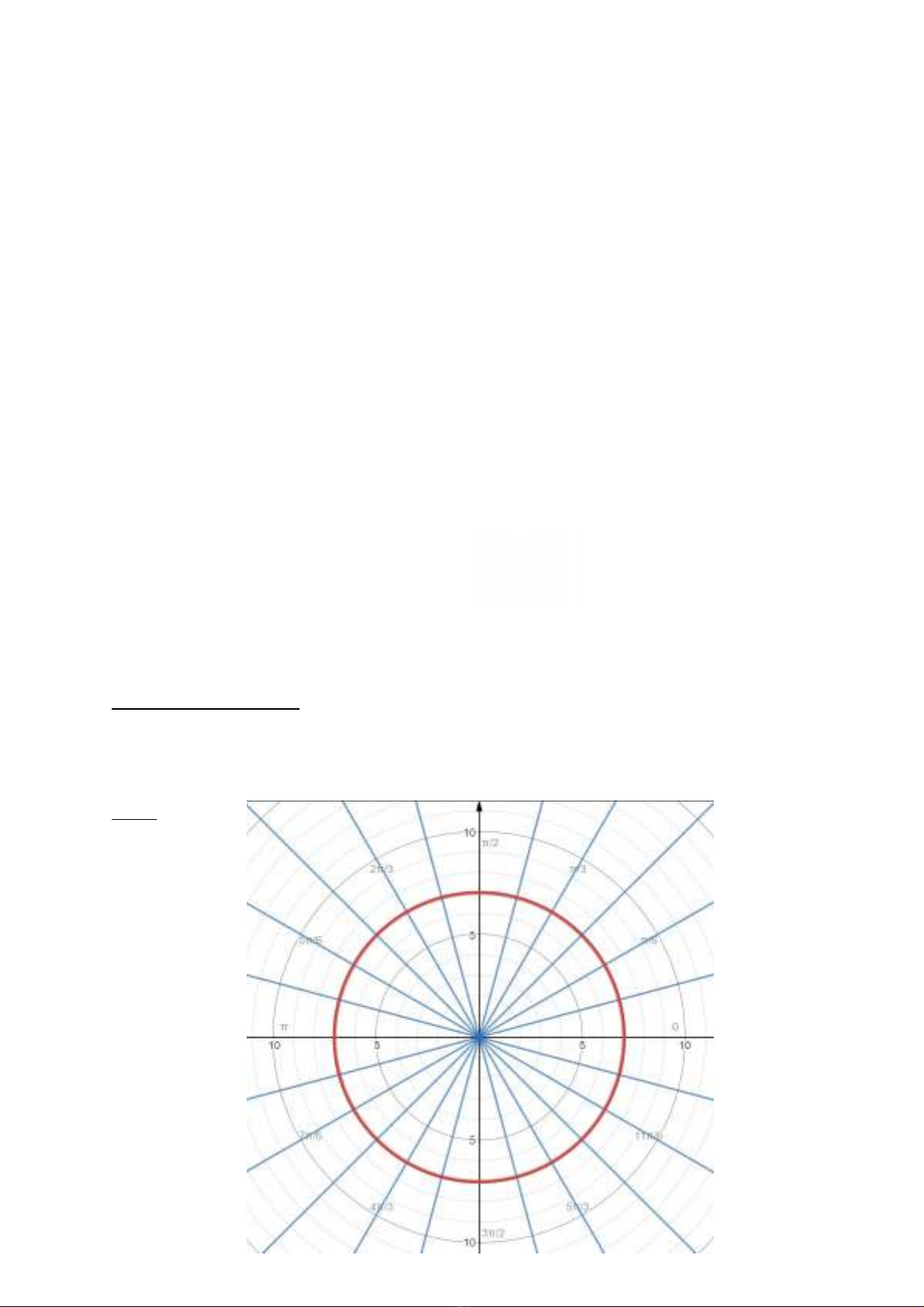
-Bán kính đc tính b ng các t l dài, t p h p các đi m có cùng bán kính đcượ ằ ỉ ệ ậ ợ ể ượ
bi u di n trên m t ph ng c c b ng các đng tròn đng tâm t i g c t a đ .ể ễ ặ ẳ ự ằ ườ ồ ạ ố ọ ộ
Ví dụ:
3
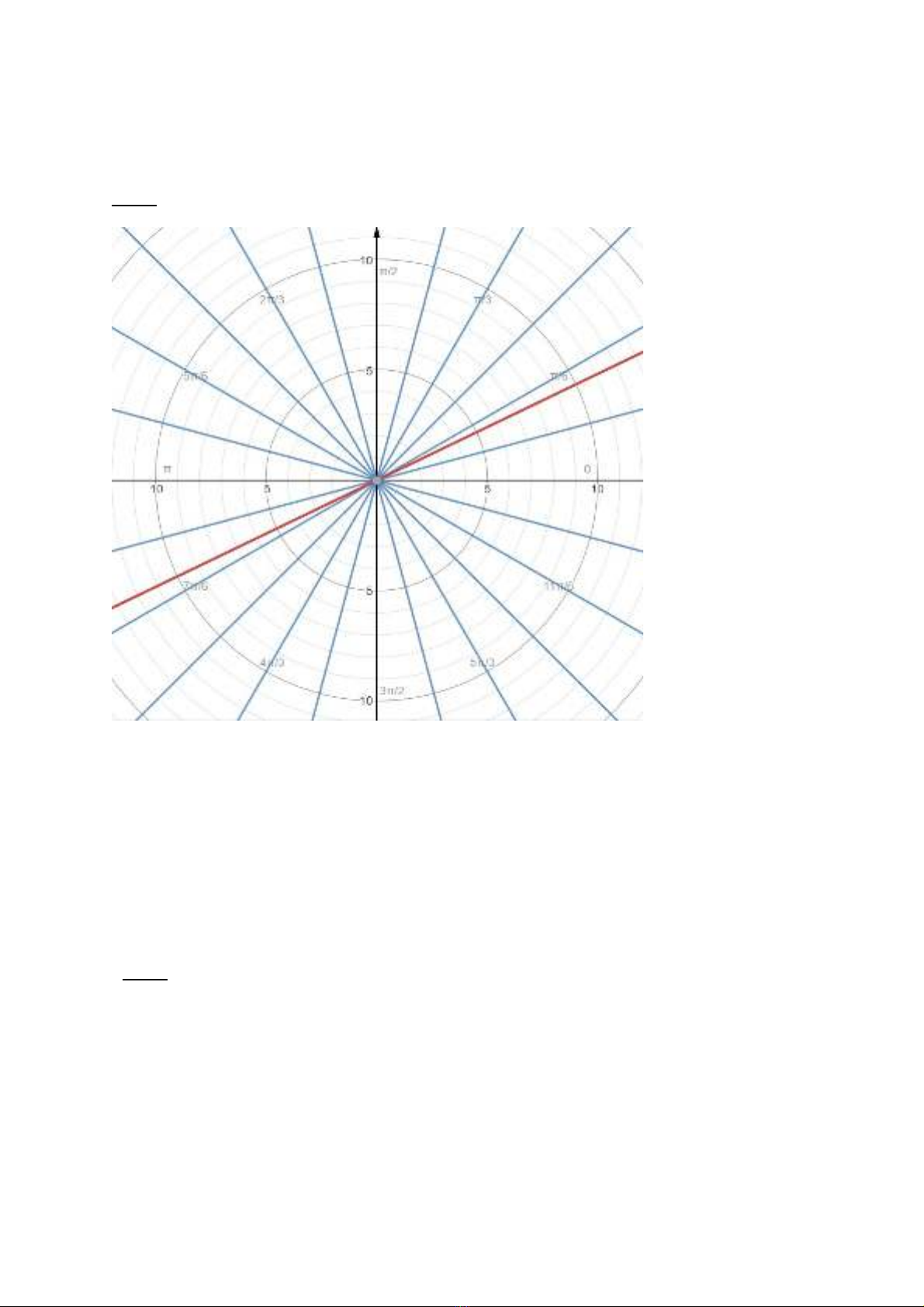
-H ng đc đo b ng đ ho c radian, chi u tăng c a h ng là chi u ng c chi uướ ượ ằ ộ ặ ề ủ ướ ề ượ ề
kim đng h , t p h p các đi m có cùng h ng là đng th ng đi qua g c t a đ vàồ ồ ậ ợ ể ướ ườ ẳ ố ọ ộ
t o v i tr c m t góc b ng . đây ta xét s đo h ng là radian.ạ ớ ụ ộ ằ Ở ố ướ
Ví dụ:
+L u ý:ư
-Khác v i h t a đ Descartes m i đi m ch đc xác đnh b i duy nh t m t c pớ ệ ọ ộ ỗ ể ỉ ượ ị ở ấ ộ ặ
giá tr , trong h t a đ c c m i đi m có nhi u cách xác đnh ng v i các giá trị ệ ọ ộ ự ỗ ể ề ị ứ ớ ị
tăng ho c gi m so v i giá tr ban đu: ặ ả ớ ị ầ
-Trong t a đ c c t n t i bán kính âm, ta có th chuy n v bán kính d ng b ngọ ộ ự ồ ạ ể ể ề ươ ằ
cách tăng ho c gi m đi t h ng cũ và đi d u : ặ ả ừ ướ ổ ấ
+Ví dụ: Tìm t t c các t a đ c c cho đi m ấ ả ọ ộ ự ể
-V i l u ý 2, m t cách bi u di n khác t a đ c c c a là ớ ư ộ ể ễ ọ ộ ự ủ
-S d ng l u ý 1 ta tìm đc 2 h giá tr t a đ c c c a là:ử ụ ư ượ ọ ị ọ ộ ự ủ
hay
4
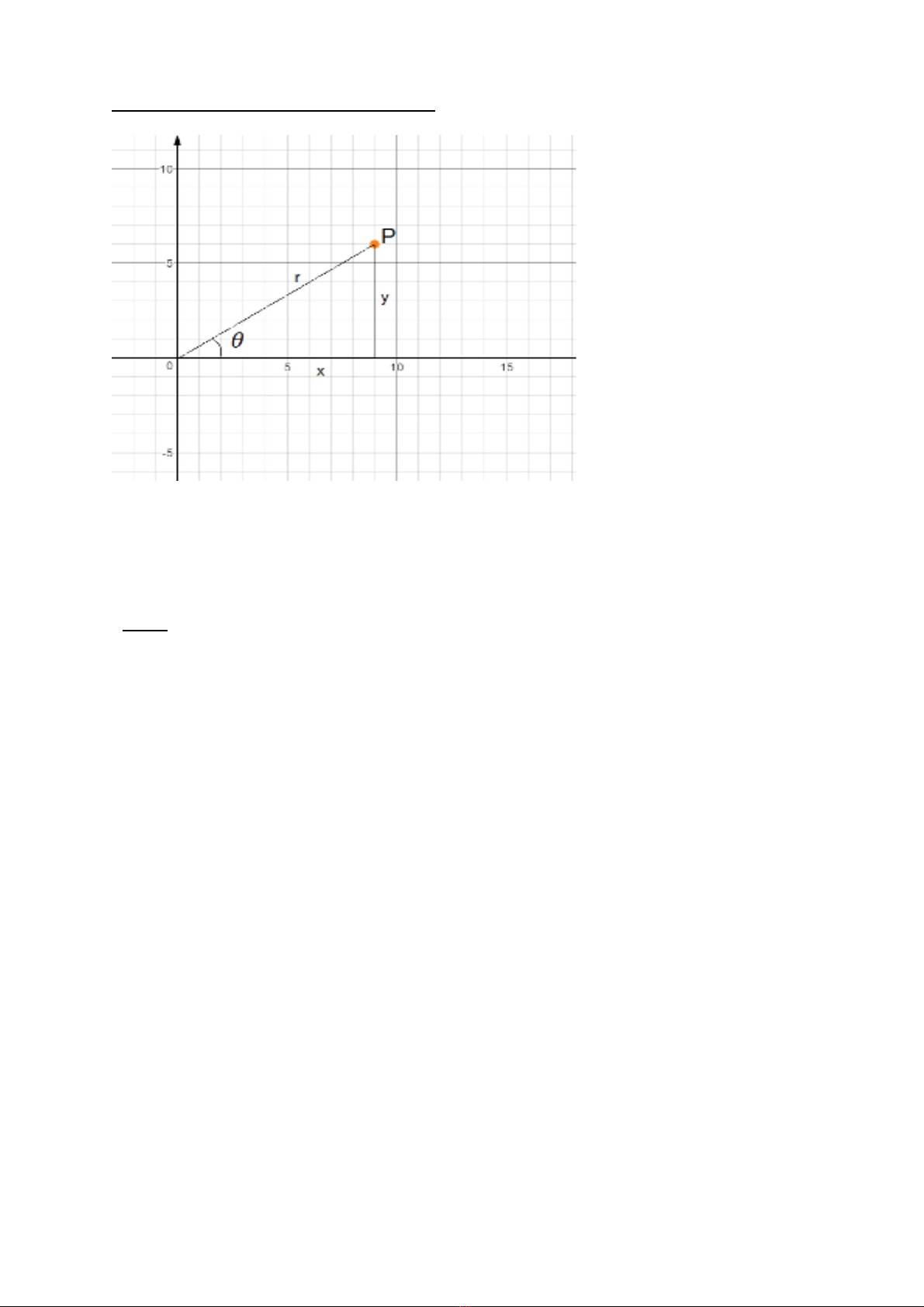
2. M i liên h v i h t a đ Descartes:ố ệ ớ ệ ọ ộ
Ta có th rút ra m i liên h gi a các giá tr và :ể ố ệ ữ ị
+Ví dụ:
1.Chuy n t t a đ c c thành t a đ Descartesể ừ ọ ộ ự ọ ộ
Ta có:
2.Chuy n t t a đ Descartes sang t a đ c c.ể ừ ọ ộ ọ ộ ự
Ta có:
là m t giá tr t a đ c c c a ộ ị ọ ộ ự ủ
3.Chuy n ph ng trình sang t a đ c c.ể ươ ọ ộ ự
Ta có:
4.Chuy n ph ng trình sang t a đ c c.ể ươ ọ ộ ự
Ta có:
II.M T VÀI VÍ D V Đ TH HÀM S TRONG T A Đ C CỘ Ụ Ề Ồ Ị Ố Ọ Ộ Ự
5