1
Chương 1
TÍN HIỆU VÀ HỆ THỐNG RỜI RẠC THỜI GIAN
Tín hiệu là sự trình bày thông tin dưới dạng dữ liệu, âm thanh, hình ảnh, video….Có nhiều cách để
phân loại tín hiệu nhưng cách ta chia tín hiệu thành dạng tương tự (liên tục theo thời gian) hoặc số (rời
rạc thời gian) . Xử lý tín hiệu là sử dụng mạch và hệ thống (gồm cả phần mềm và phần cứng) để tác
động lên đầu vào và nhận tín hiệu ngõ ra theo cách mà chúng ta mong muốn.
Hệ thống số có rất nhiều điểm thuận lợi hơn so với hệ thống liên tục chẳng hạn không có nhiễu, dễ cất
dữ và truyền đi. Để chuyển một tín hiệu liên tục sang dạng số, ta phải lấy mẫu tín hiệu, lượng tử và
mã hóa giá trị sang dạng nhị phân. Tín hiệu lấy mẫu gọi là tín hiệu rời rạc thời gian. Tuy nhiên, để sử
lý tín hiệu trong hệ thống số (chẳng hạn như máy tính), có thể thực hiện được tất cả ba bước trên.
Thông thường hai bước cuối, lượng tử và mã hóa nhị phân được hiểu ngầm, vì vậy cụm từ rời rạc thời
gian và số tương đương và hoán đổi cho nhau.
Bên cạnh tín hiệu mà ta mong muốn, ở đây cũng có những thành phần không được hoan
nghênh như nhiễu, can nhiễu …..những thành phần này chúng ta muốn loại bỏ hoặc tối thiểu hóa.
Hệ thống có thể là mạch logic đơn giản, những chương trình đơn giản, hoặc những cấu trúc
phức tạp bao gồm cả phần cứng và phần mềm như máy tính. Chúng ta sẽ thảo luận những loại hệ
thống số khác nhau. Ở đây giả sử hệ thống là tuyến tính và bất biến đổi theo thời gian . Một hệ thống
mẫu thường thấy là những bộ lọc.
1.1 TÍN HIỆU LIÊN TỤC THỜI GIAN CONTINUOUS – TIME SIGNALS
Là một tín hiệu có sự biến đổi biên độ theo thời gian. Biên độ có thể là hiệu điện thế, dòng, công
suất… Tuy nhiên trong mạch và hệ thống, biên độ thường được trình bày dưới dạng hiệu điên thế.
Tín hiệu liên tục theo thời gian (hay tín hiệu analog) có biên độ biến đổi khác nhau theo thời
gian. Chúng thường được tạo ra bởi mạch điện tử, những nguồn tự nhiên như nhiệt, âm thanh,
video…và được chuyển thành tín hiệu điện tử bằng những đầu dò và bộ chuyển đổi. Tín hiệu được
minh họa bằng dạng sóng để dễ dàng quan sát.
1.1.1 Trình bày toán học của tín hiệu
Thay vì mô tả tín hiệu bằng từ ngữ hoặc dạng sóng, cách cụ thể và chính xác hơn là diễn tả dưới dạng
toán học. Sự trình bày toán học của tín hiệu trong miền thời gian và miền biến đổi thì cần thiết cho sự
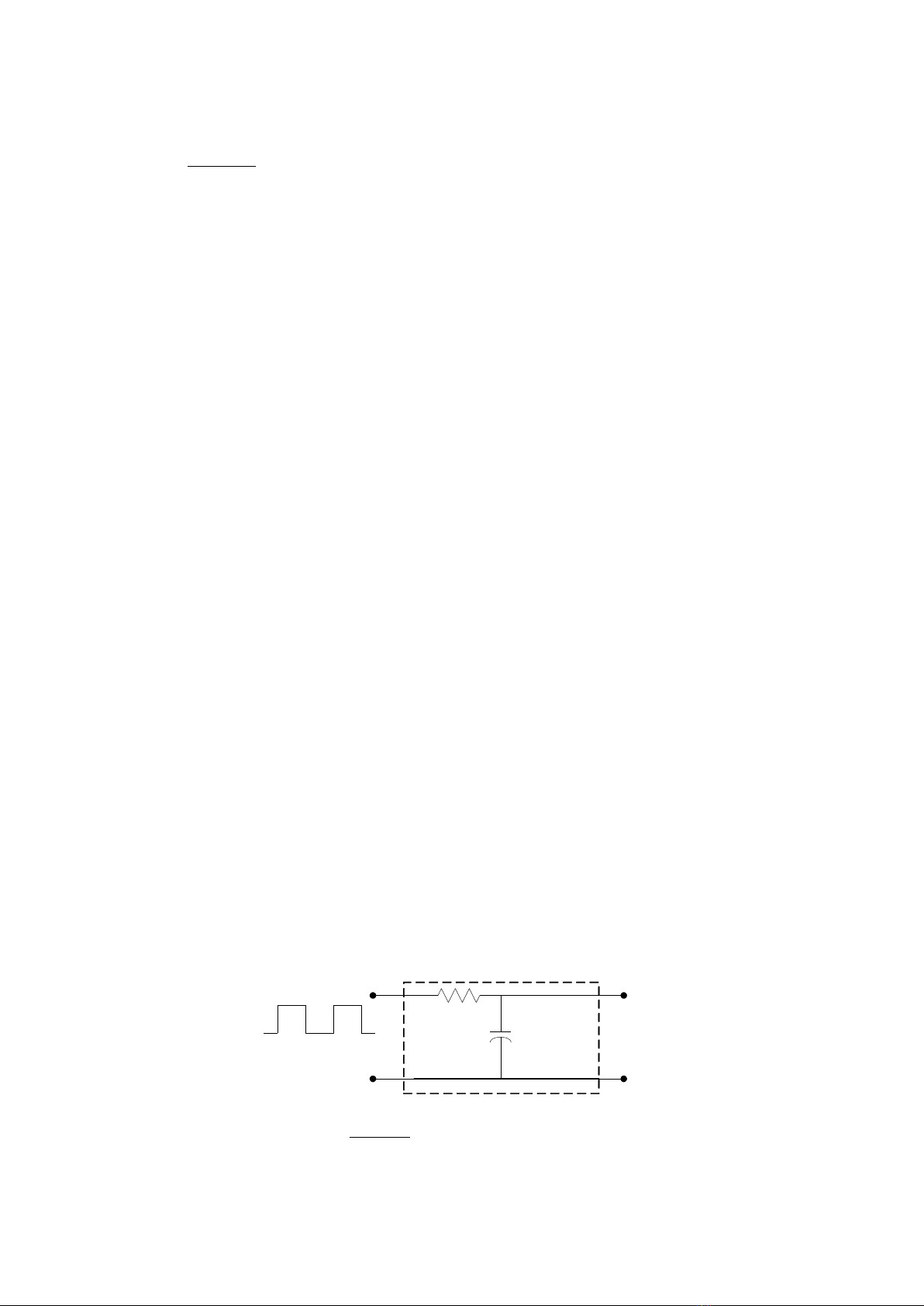
phân tích , thiêt kế mạch và hệ thống. Một ví dụ đơn giản ở hình 1.1 không thể giải quyết bằng ngôn
ngữ miêu tả hoặc mạch.
R
C
0,1F
Maïch
Vaøo Ra
1Vññ - 1kHz
Hình1.9: Baøi toaùn phaân tích
?
560Ω
Circuit
Input
Output
Hình.1.1:Ngõ ra tín hiệu là gì?
0.1F
1Vpp – 1kHz
2
Tín hiệu sin
Tín hiệu Sin hoặc sóng sin là tín hiệu tương tự phổ biến nhất. (Hình 1.2). Nó nhẵn, dễ tạo, có nhiều
thuộc tính và ứng dụng. Diễn tả toán học được cho bởi.
x(t) = Acos(
t + o) (1.1)
Ở đây A là giá trị đỉnh, Ω là tần số gốc (radians/s), t là thời gian (sec), Φo là pha ban đầu (radians) là
phase khi t = 0, Ω = 2F với F là tần số (Hz), T = 1 / F = 2/Ω là chu kỳ (sec).
Sự diễn tả bên trên chứa tất cả những đối số cần thiết: biên độ (đỉnh, rms, trung bình), và sự
tuần hoàn (chu kỳ, tần số). Ngược lại, dạng sóng, ngoại trừ giá trị hằng số thì không có tính cô động.
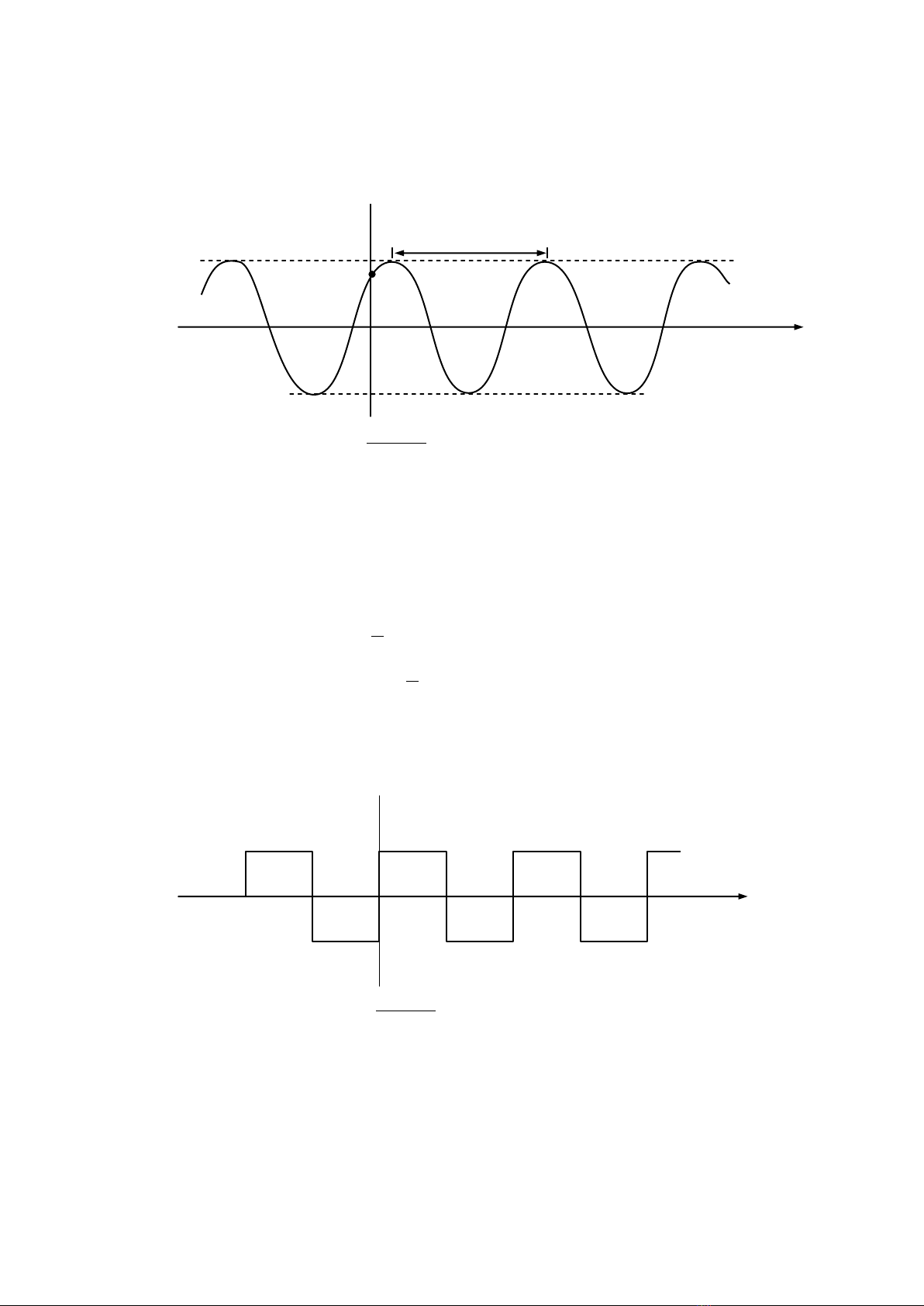
Ví dụ: Cho sóng vuông (hình 1.3) biểu thức toán học gồm một phần cho biên độ, một phần cho sự tuần
hoàn.
x(t) = –A ,
0
2 t
T
(1.2)
+A ,
2
0T
t
x(t) = x(t nT) , n = 1, 2, 3 …
Sóng Sin và vuông là xác định. Với những tín hiệu ngẫu nhiên, nhìn chung ta không thể trình bày dạng
toán học của chúng. Nhiễu điện và can nhiễu là những ví dụ của tín hiệu ngẫu nhiên.
1.1.2 Một số tín hiệu đặc biệt
Ở đây có hai tín hiệu thường được sử dụng trong phân tích mạch và xử lý tín hiệu.
(a) Xung đơn vị
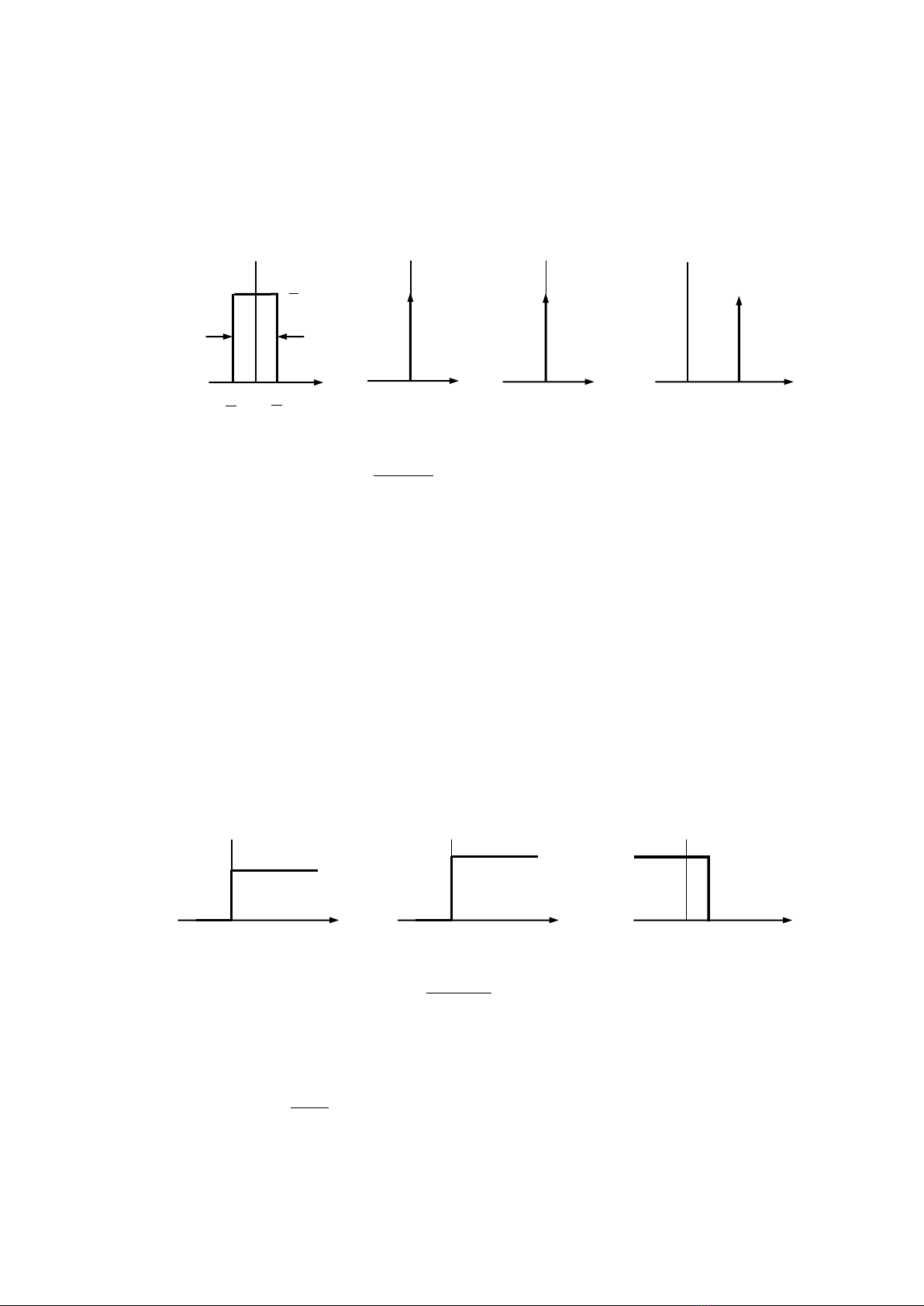
Xung đơn vị (Hàm delta Dirac) là hình thức cải tiến từ một xung chữ nhật đối xứng với độ rộng xung
và biên độ
/1
khi
→ 0 (Hình.1.4). Biểu diễn toán học
(t) = , t = 0
x(t)
0
t
T
A
–A
Acos0
Hình.1.2: Tín hiệu sin
x(t)
A
–A
t
0
T
T/2
2T
–T/2
Hình.1.3: Sóng vuông đối xứng
3
0 , t 0
dtt)(
= 1 (1.3)
Theo định nghĩa này,
(–t) = (t) (1.4)
Xung có biên độ A thay vì 1ta viết A
(t) (Hình.1.4c). Nếu xung đơn vị chậm đi to, ta có
(t – to)
(Hình.1.4d), thì:
(t – tO) = , t = tO (1.5)
0 , t tO
2
1)()( t
tOO dtttdttt
= 1, t1 < tO < t2
Một tín hiệu x(t) khi nhân với xung đợn vị trễ thời điểm to
)( 0
tt
có giá trị x(to) tại to:
x(t)(t – to) = x(to) (1.6)
(b) Bậc đơn vị:
Hình 1.5 là bậc đơn vị. Tín hiệu tăng đột ngột từ 0 lên 1 tại thời điểm t=0, sau đó duy trì không đổi.
Hoạt động giống với sự đóng mở của một công tắc điện tử. Diễn tả công thức toán học:
u(t) = 0 , t < 0
1 , t 0 (1.7)
[
Xung đơn vị
(t) và bậc đơn vị u(t) liên hệ với nhau như sau:
tdtttu ')'()(
= 0 , t < 0
1 , t 0 (1.8a)
dt
tdu
t)(
)(
(1.8b)
1
0
t
2
2
0
t
(t)
A(t)
(t-t0)
0
t
0
t0
t
(a)
(b)
(c)
(d)
Hình.1.4: Xung đơn vị
)(t
0
Au(
0
t
– t)
1
A
A
0
0
Au(t)
u(t)
t
t
t
(a)
(b)
(c)
Hình.1.5: Bậc đơn vị
4
1.1.3 Tín hiệu phức
Đại lượng vật lý tự nhiên, bao gồm tín hiệu là những giá trị thực. Tuy nhiên thỉnh thoảng tín hạng ảo j
=
1
được thêm vào để tạo sự thuận tiện về mặt toán học, chẳng hạn như tính toán sự khác nhau về
phase của hiệu điện thế và dòng trong mạch điện AC. Sau đây là một tín hiệu phức:
x(t) = 5cos
t – j5sin
t
Một tín hiệu phức bao gồm phần thực và phần ảo.
x(t) = x
R
(t) + jx
I
(t) (1.9)
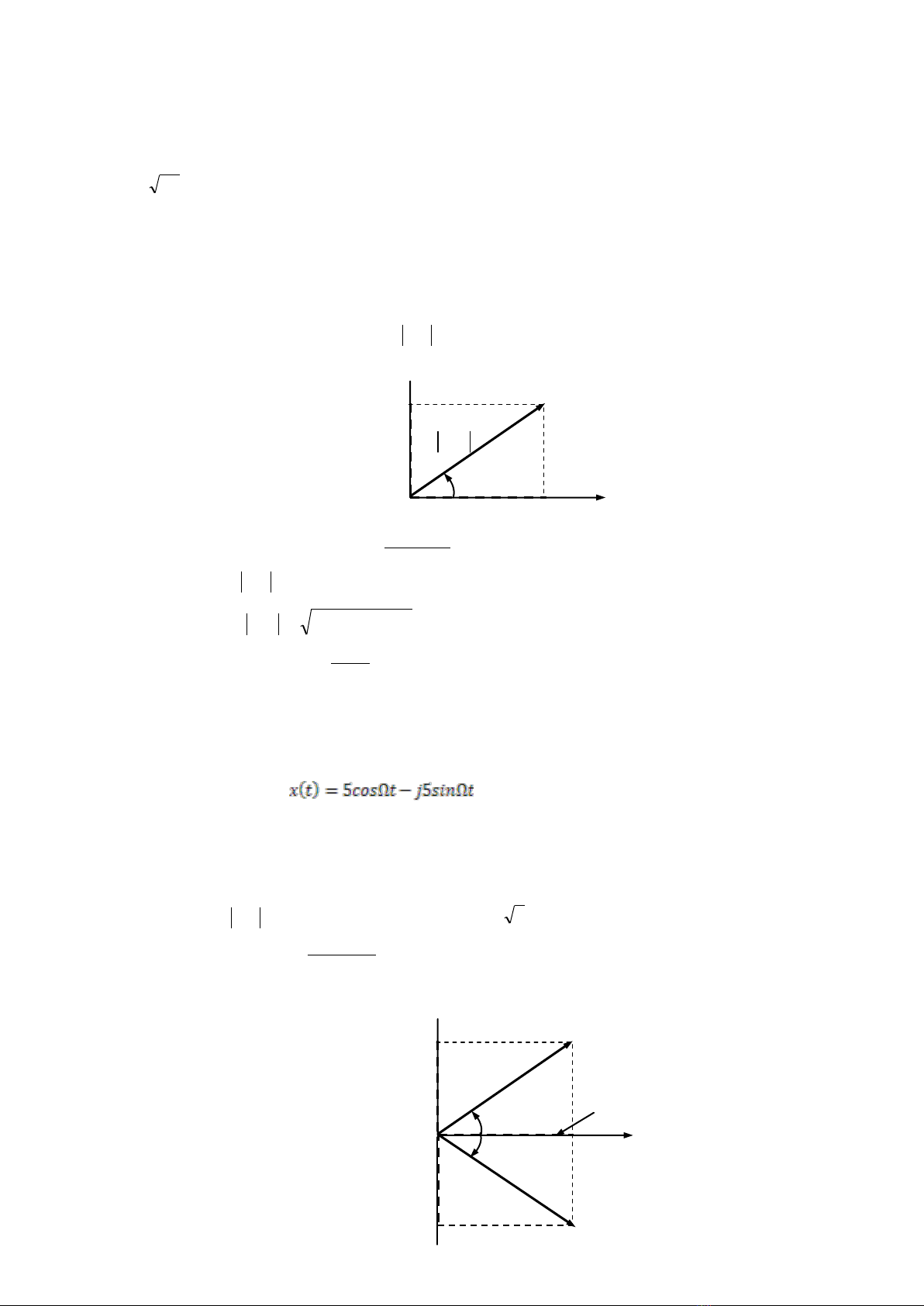
Trong hệ tọa độ cực, một tín hiệu phức có thể diễn tả gồm thành phần biên độ và pha (Hình.1.6)
x(t) = x
R
(t) + jx
I
(t) =
)(
)( tj
etx
(1.10)
Ký hiệu độ lớn
)(tx
và phase
)Φ(t
hoặc argx(t) hoặc
x(t). Ta có:
)t(x)t(x)( 2
I
2
Rtx
(1.11a)
)(
)(
tan)Φ( 1
tx
tx
t
R
I
(1.11b)
Chú ý độ lớn là giá trị tuyệt đối, trong khi biên độ là giá trị có dấu, nhưng ta cũng không cần chú ý tới
sự khác nhau của hai thành phần này
Ví dụ 1.1.1
Cho một tín hiệu phức . Tìm phần thực, phần ảo, độ lớn và phase.
Giải:
– Phần thực: x
R
(t) = 5cos
t
– Phần ảo: x
I
(t) = –5cos
t
– Độ lớn:
ttt(tx cosΩ25)cosΩ5()cosΩ5)( 2/1
22
– Phase:
)1(tan
cosΩ5
cosΩ5
tan)Φ( 11
t
t
t
= –450 Không phụ thuộc t
Theo sự diễn tả này ta có thể xem một tín hiệu phức như một vector và viết x(t)
-(t)
(t)
Ảo
Thực
xI(t)
x(t)
x*I(t)
0
x*(t)
xR(t) = x*R(t)
Ảo
Thực
x
R
(t)
(t)
(t)
)(tx
x
I
(t)
x(t)
Hình.1.6: Tín hiệu phức và tọa độ cực
0
5
Hai đại lượng phức có cùng phần thực nhưng đối nhau phần ảo là liên hiệp phức của nhau (Hình 1.7).
Vì vậy, với một tín hiệu phức x(t), thì liên hiệp phức của nó là công thức (1.12),
x*(t) = xR(t) – jx(t) =
)(
)( tj
etx
(1.12)
1.1.4 Tín hiệu mũ phức
Công thức (1.1) là một tín hiệu sin thực. Mũ phức, hay Sin phức thì phổ biến hơn. Biểu diễn chung:
)( 0
)(
tj
Aetx
(1.13)
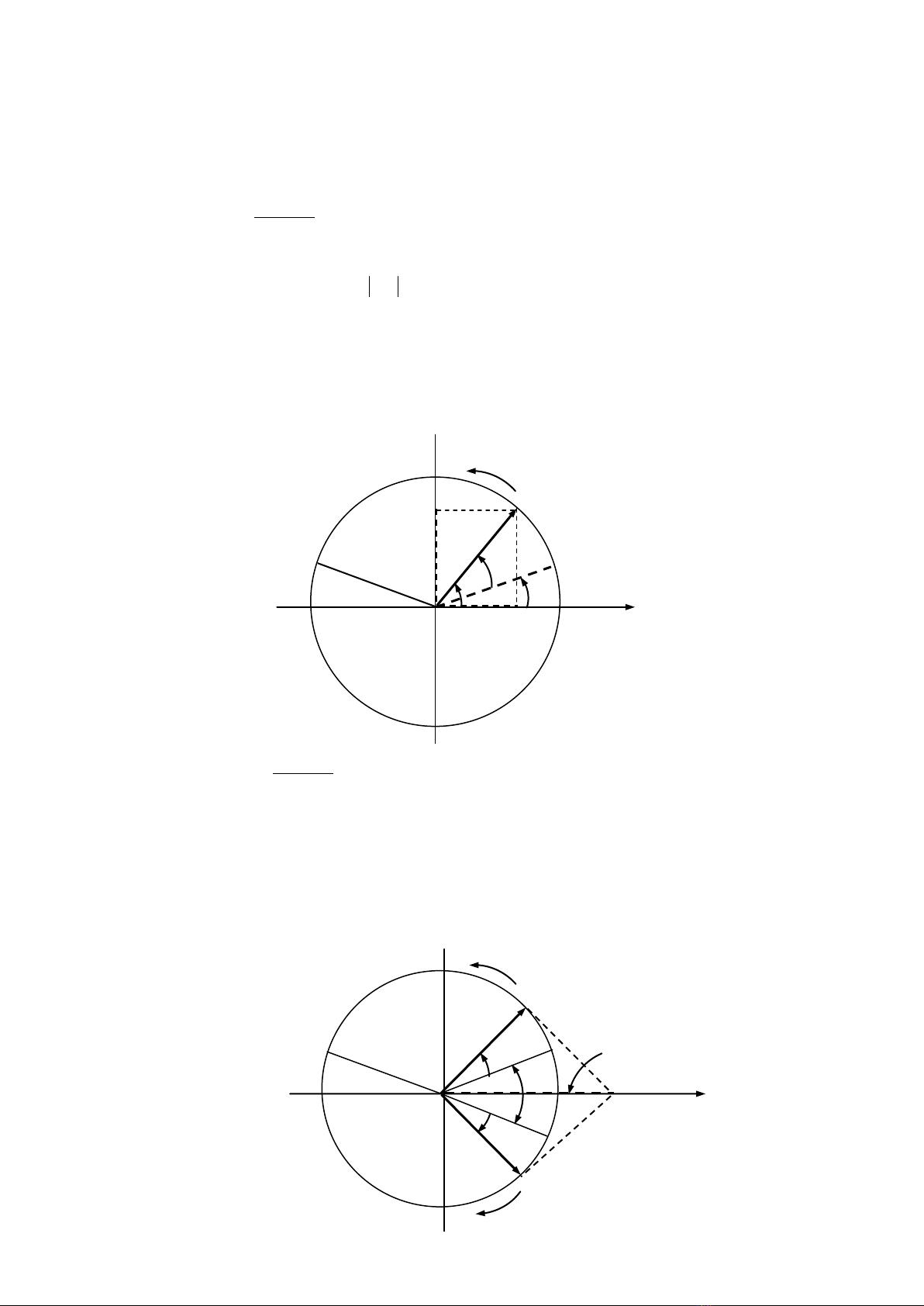
[]Phasor là trình bày vector của tín hiệu (Hình.1.8). Nó tuần hoàn với chu kỳ 2 radians.
Từ một mũ phức, phần sin thực được dẫn xuất bởi hai cách. Đầu tiên lấy phần thực
R
x
(t) = Re[Acos(
t + o) + jAsin(
t +
o)]
= Acos(
t + o)
(1.14)
Hình.1.7: Tín hiệu phức x(t) và liên hiệp phức x*(t)
Ảo
A
x(t)
t
Thực
0
-0
-
-
t
x*(t)
2xR(t)
Ảo
xI(t)
A
x(t)
t
t
xR(t)
Thực
(t=0)
0
Hình.1.8: Trình bày Phasor dạng mũ
0