1
LỜI NÓI ĐẦU 3
CHƯƠNG I . GIẢI BÀI TOÁN ĐỘNG HỌC 4
1.1. Giải bài toán động học thuận 4
1.1.1. Cơ sở lý thuyết 4
1.1.2. Thiết lập phương trình động học thuận cho robot RRR. 9
a. Tìm các ma trận biến đổi 9
b. Xác định vị trí và hướng của bàn kẹp 10
c. Xác định vận tốc của điểm tác động cuối so với hệ cố định 11
d. Vận tốc góc của mỗi khâu so với hệ cố định 11
e. Các đồ thị thể hiện vị trí, vận tốc điểm tác động cuối E 11
1.2. Giải bài toán động học ngƣợc 12
1.2.1. Giải bài toán động học ngược bằng phương pháp giải tích 13
a. Cơ sở lý thuyết 13
b. Áp dụng giải bài toán ngược cho robot RRR 14
1.2.2. Giải bài toán ngược bằng phương pháp số 17
a. Cơ sở lý thuyết 17
b. Áp dụng giải bài toán cho robot RRR 19
CHƯƠNG II. GIẢI BÀI TOÁN TĨNH HỌC ROBOT 21
2.1. Cơ sở lý thuyết 21
2.2. Áp dụng cho Robot RRR 22
CHƯƠNG III. THIẾT KẾ QUỸ ĐẠO CHUYỂN ĐỘNG CHO ROBOT 27
3.1 Giới thiệu và cơ sở thiết kế quỹ đạo 27
3.2. Tính toán thiết kế quỹ đạo chuyển động 27
3.2.1 Thiết kế quỹ đạo trong không gian khớp 27
3.2.2. Thiết kế quỹ đạo trong không gian làm việc 29
a. Quỹ đạo của điểm tác động cuối theo đường thẳng từ A đến B trong tc (s) 30
b. Thiết kế quỹ đạo điểm tác động tác động cuối di chuyển theo đường tròn từ A
đến B trong
c
ts
lấy AB làm đường kính. 32
CHƯƠNG IV. ĐỘNG LỰC HỌC ROBOT 34
2
4.1. Cơ sở lý thuyết 34
4.2. Áp dụng tìm phƣơng trình vi phân cho Robot RRR 36
4.2.2. Bảng tham số động học 36
4.2.3. Các phương trình vi phân 36
III. ĐIỀU KHIỂN ROBOT 37
5.1. Điều khiển phản hồi và điều khiển vòng kín. 37
5.2. Thiết kế bộ điều khiển PID 38
5.3. Thiết kế bộ điều khiển trong không gian khớp 40
KẾT LUẬN 44
TÀI LIỆU THAM KHẢO 45
3
LỜI NÓI ĐẦU
Khi xét về vấn đề Robot chúng ta đặt ra các bài toán: động học Robot, động lực học
Robot và điều khiển Robot. Đây là những bước cơ sở ban đầu hết sức quan trọng trước khi
thiết kế Robot.
Với sự phát triển như vũ bão của công nghệ thông tin như ngày này, rất nhiều các lĩnh
vực trong cơ khí đã tận dụng được sự phát triển này để tạo ra những bước nhảy vọt, rong đó
có công nghiệp Robot.
Trên cơ sở đó, môn học Robotics đã mang lại cho sinh viên những kiến thức vô cùng
quan trọng cho sinh viên chúng em. Bên cạnh đó, nó cũng tạo ra một cơ hội để sinh viên được
tiếp cận với những phần mềm tính toán, mô phỏng phổ biến trên thế giới hiện nay như Maple
và Matlab.
Để thực hiện được bài tập lớn này, em xin chân thành cảm ơn thầy giáo, PGS.TS Phan
Bùi Khôi đã tận tình, chu đáo dạy học trên lớp. Em xin chân thành cảm ơn thầy.
4
CHƢƠNG I . GIẢI BÀI TOÁN ĐỘNG HỌC
1.1. Giải bài toán động học thuận
1.1.1. Cơ sở lý thuyết
Vị trí mỗi khâu trong không gian được xác định bởi vị trí một điểm định vị và hướng
của khâu đó đối với một hệ quy chiếu đã chọn. Điểm định vị là một điểm xác định nào đó của
khâu, thông thường trong động lực học ta hay lấy khối tâm của khâu đó làm điểm định vị.
Hướng của khâu được xác định bằng ma trận cosin chỉ hướng hoặc bằng các tọa độ suy rộng
xác địnhvị trí của vật rắn quay quanh một điểm.
Động học robot nghiên cứu chuyển động của các khâu của robot về phương diện hình
học, không quan tâm đến các lực và momen gây ra chuyển động.Động học robot là bài toán
qua trọng phục vụ tính toán và thiết kế robot.Nhiệm vụ chủ yếu của bài toán động học thuận
là xác định vị trí và hương của bàn kẹp dưới dạng hàm của biến khớp.
Các phương pháp ma trận 4x4 và các phương pháp ma trận 3x3 hay được sử dụng trong
phân tích động học robot. Hai phương pháp ma trận 4x4 phổ biến là phương pháp ma trận
Denavit-Hartenberg và phương pháp ma trận Craig. Trong báo cáo này chúng em trình bày và
áp dụng phương pháp ma trận Denavit-Hartenberg để tính toán động học robot.
Giải bài toán động học thuận robot công nghiệp bằng phương pháp ma trận Denavit-
Hartenberg
Cách xác định các trục cuả hệ tọa độ khớp.
Đối với robot công nghiệp ,Denavit-Hartenberg đã đưa ra cách chọn các hệ trục tọa độ
có gốc tại khớp thứ i như sau:
Trục
1i
z
được chọn dọc theo hướng của trục khớp động thứ i.
Trục
1i
x
được chọn dọc theo đường vuông góc chung của 2 trục
2i
z
và
1i
z
hương đi
từ trục
2i
z
sang trục
1i
z
. Nếu trục
1i
z
cắt trục
2i
z
thì hướng của trục
1i
x
được chọn tùy ý
miễn là vuông góc với trục
1i
z
.Khi 2 trục
2i
z
và
1i
z
song song với nhau, giữa 2 trục này
có nhiều đường vuông góc chung , ta có thể chọn trục
1i
x
hướng theo pháp tuyến chung nào
cũng được.
Gốc tọa độ
1i
O
được chọn tại giao điểm cuả trục
1i
x
và trục
1i
z
.
Trục
1i
y
được chọn sao cho hệ
1
( x )i
O yz
là hệ quy chiếu thuận.
5
Hệ tọa độ
1
( x )i
O yz
được xác định như trên trong một số tài liệu được quy ước là hệ
tọa độ khớp.
Chú ý: Với cách chọn hệ tọa độ như trên , đôi khi hệ tọa độ khớp
1
( x )i
O yz
không
được một cách duy nhất. vì vậy, ta có một số bổ sung thích hợp như sau.
Đối với hệ tọa độ
0
( x )O yz
theo quy ước trên ta mới chỉ chọn được trục
, còn trục
chưa có trong quy ước trên.Ta có thể chọn trục
một cách tùy ý, miễn là
vuông góc
với
.
Đối với hệ tọa độ
( x )n
O yz
, do không có khớp (n+1) nên theo quy ước trên ta không
xác định
. Trục
không được xác định duy nhất, trong khi trục
lại được chọn theo
đường pháp tuyến của trục
1n
z
. Trong trường hợp này, nếu khớp n là khớp quay, ta có thể
chọn trục
song song trục
1n
z
. Ngòai ra ta có thể chọn tùy ý sao cho hợp lý.
Khi khớp thứ i là tịnh tiến, về nguyên tắc ta có thể chọn trục
1i
z
một cách tùy ý. Tuy
nhiên trong nhiều trường hợp người ta thường chọn trục
1i
z
dọc theo trục cuả khớp tịnh tiến
này.
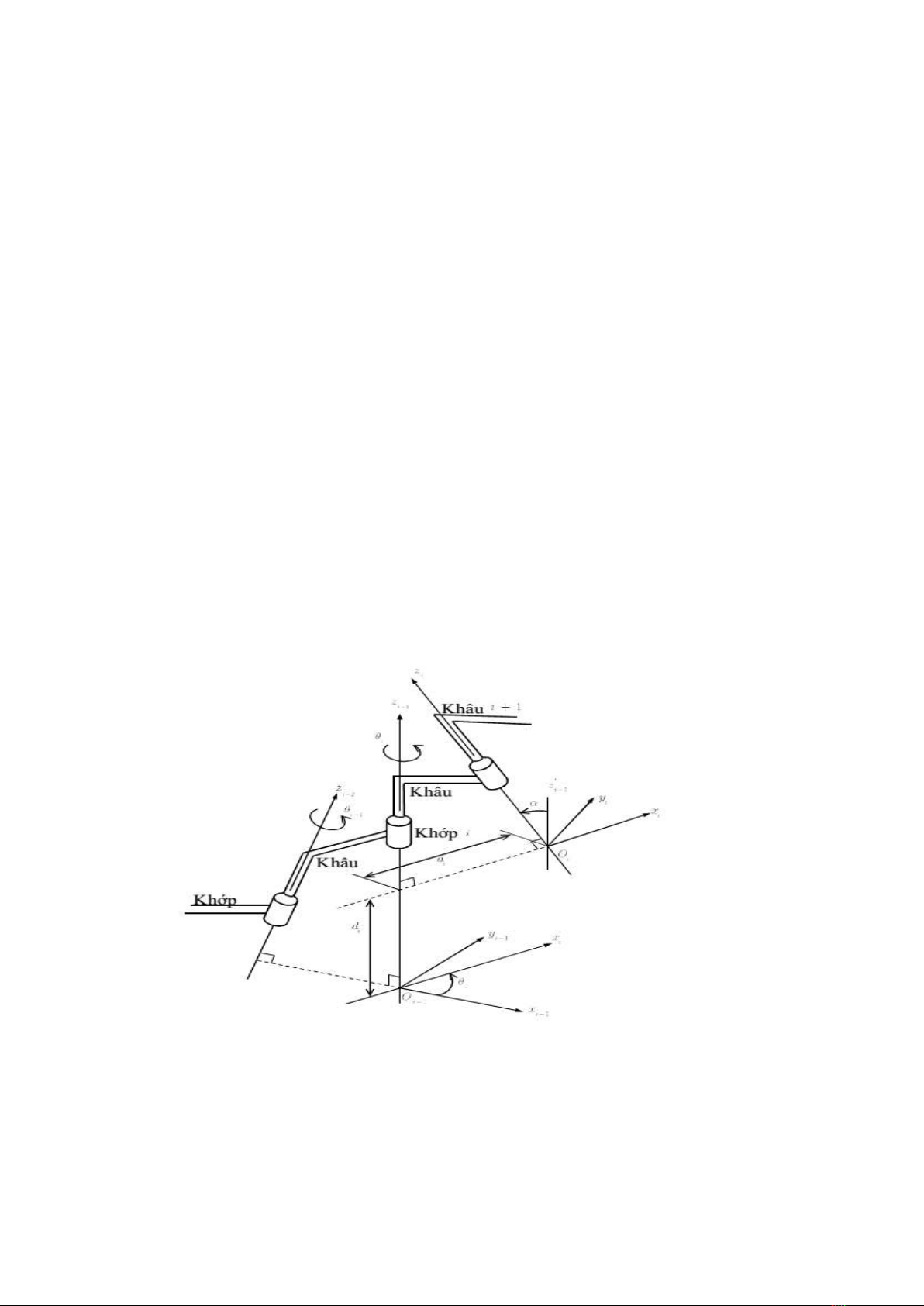
Hình 1.1.diễn các thông số Denavit-Hartenberg giữa các trục hệ tọa độ
Các tham số động học Denavit-Hartenberg